归并排序（Java代码）_java归并排序算法代码

一、核心思想

归并排序核心思想就是：将一个待排序的数列拆分成多个长度为1的数列；然后再将这些长度为1的数列两两合并成长度为2的多个有序数列，接着再把这些长度2和有序数列两两合并成长度为4的有序数列…直到合并为原数列长度的有序数列。所以归并排序主要有连个步骤：”从下往上的分解“和”从上往下的合并“（如下图实例）

二、实例

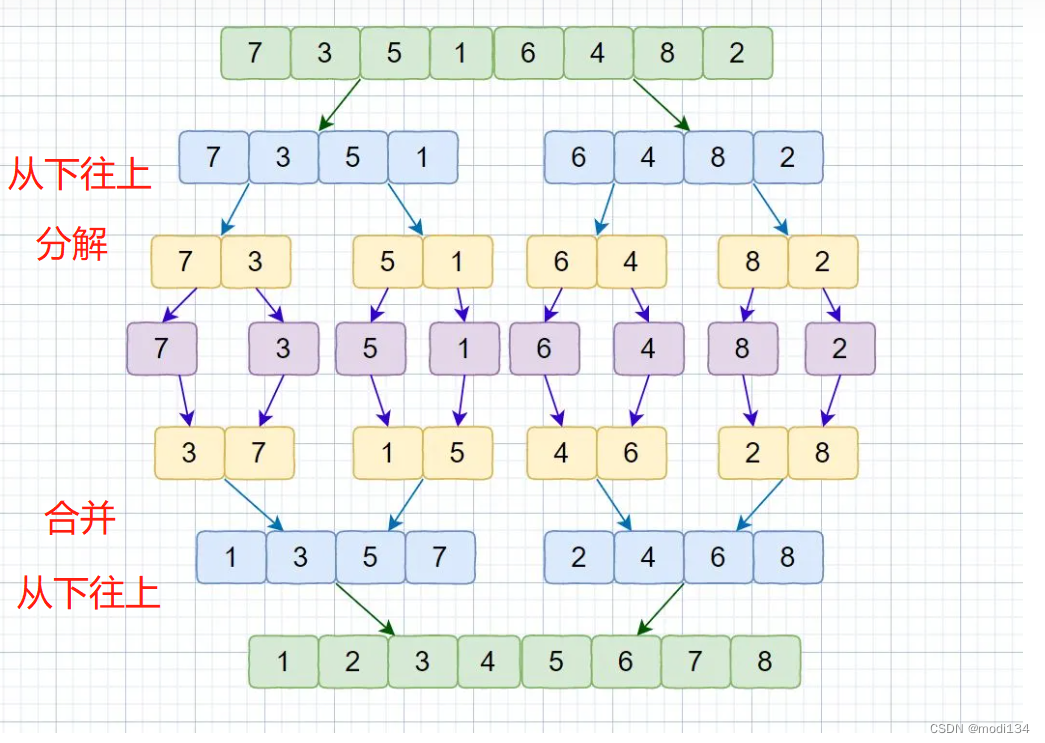
图片截至：https://zhuanlan.zhihu.com/p/452169920

三、代码实现（java）

public class Sort {
    /**
     * 归并排序(从上往下（分）)拆分
     * @param nums 待排序数组
     * @param l 数组左边界（起始为0）
     * @param r 数组右边界(起始为数组长度 -1)
     *  @param temp 用作中转的数组
     * @return
     */
    public int[] mergeSortTopDown(int[] nums, int l, int r, int[] temp) {
        //递归结束条件，当l=r时数组被拆分成只有1个数，就拆到底了
        if (l < r) {
            int m = (l + r) / 2;
            //递归拆分前一半
            mergeSortTopDown(nums,l,m,temp);
            //递归拆分后一半
            mergeSortTopDown(nums,m+1,r,temp);
            //合并
            mergeSortBottomUp(nums,l,m,r,temp);
        }
        return temp;
    }

    /**
     *  归并排序(从下往上（治）)合并
     * @param nums
     * @param l 下标l~m为有序待合并“数组”1
     * @param m
     * @param r 下标m+1~r为有序待合并“数组”2
     * @param temp 用作中转的数组
     * @return
     */
    public int[] mergeSortBottomUp(int[] nums, int l, int m, int r,int[] temp) {
        int i = l, k = l, j = m + 1;
        //将两“数组”按照从小到大合并到temp数组
          //直到两个数组当中的其中一个处理完毕
        while (i <= m && j <= r) {
            if (nums[i] < nums[j]) {
                temp[k++] = nums[i++];
            } else {
                temp[k++] = nums[j++];
            }
        }
        //如果第一个“数组“中有剩余，将剩下的数合并到temp数组
        while (i <= m) {
            temp[k++] = nums[i++];
        }
        //如果第二个“数组“中有剩余，将剩下的数合并到temp数组
        while (j <= r) {
            temp[k++] = nums[j++];
        }
        //将排序完成的后的结果数组temp，赋值到原数组对应下标位置
          //不做这一步处理的话，下一级排序合并又是在原数组基础上处理，是错误的
        while (l <= r) {
            nums[l] = temp[l];
            l++;
        }
        return temp;
    }
  }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60