k-means聚类算法原理简析_kmeans聚类算法原理

概要

K-means算法是最普及的聚类算法，也是一个比较简单的聚类算法，所以刚接触的同学不要感到害怕。算法接受一个未标记的数据集，然后将数据聚类成不同的组，同时，k-means算法也是一种无监督学习。

算法思想

k-means算法的思想比较简单，假设我们要把数据分成K个类，大概可以分为以下几个步骤：

1. 随机选取k个点，作为聚类中心；
2. 计算每个点分别到k个聚类中心的聚类，然后将该点分到最近的聚类中心，这样就行成了k个簇；
3. 再重新计算每个簇的质心（均值）；
4. 重复以上2~4步，直到质心的位置不再发生变化或者达到设定的迭代次数。

算法流程图解

下面我们通过一个具体的例子来理解这个算法（我这里用到了Andrew Ng的机器学习教程中的图）：
假设我们首先拿到了这样一个数据，要把它分成两类：

我们人眼当然可以很快的分辨出来，可以在两个聚类间找到一条合理的分界线，那么用k-means算法来解决这个问题会是怎样的呢？
首先我们随机选取两个点作为聚类中心（因为已经明确是分为两类）：

接下来就可以开始计算每个点到红点和蓝点的距离了，离红点近就标记为红色，离蓝点近就标记为蓝色。结果为下图：

很明显，这样完全不是我们想要的结果，接下来我们进行第三步，重新计算聚类中心的位置。

红X和蓝X都向中间靠拢了一点。我们可以看到，聚类中心发生改变后，其他点离两个聚类中心的距离也跟随着发生了变化。然后我们重复第二步，根据每个点到两个聚类中心的距离远近来进行重新分类，离红X近的归为红类，离蓝X近的归为蓝类。

之前站错了队伍的一些点重新进行了调整，现在的分类离我们的目标越来越近了，但还没有达到最佳的分类效果。接下来继续重复上面的步骤，重新计算聚类中心的位置，再重新分类，不断迭代，直至聚类中心的位置不再变化（变化范围达到设定值）或达到迭代次数为止。

这样我们就利用k-means算法把这个数据很好的分为两类啦。
我们可以看到，在整个过程中，我们都没有去监督算法，告诉他具体是分错了还是对了，只是在开始的时候告诉他要把这个数据分成多少类，然后后面的操作都是由他自己完成，完全没有人为的让他进行分类的学习，也没有帮助他纠正错误，所以k-means算法也是一种无监督学习方法。

相信看到这里你对k-means算法的原理也有了一个大概的了解啦。下面我们再来看看这个算法的代码实现吧。

代码实现

下面就放一个Andrew Ng 机器学习教程的习题答案吧，把k-means算法的具体流程大概实现了一下：

function [centroids, idx] = runkMeans(X, initial_centroids, ...
                                      max_iters, plot_progress)
%RUNKMEANS runs the K-Means algorithm on data matrix X, where each row of X
%is a single example
%   [centroids, idx] = RUNKMEANS(X, initial_centroids, max_iters, ...
%   plot_progress) runs the K-Means algorithm on data matrix X, where each 
%   row of X is a single example. It uses initial_centroids used as the
%   initial centroids. max_iters specifies the total number of interactions 
%   of K-Means to execute. plot_progress is a true/false flag that 
%   indicates if the function should also plot its progress as the 
%   learning happens. This is set to false by default. runkMeans returns 
%   centroids, a Kxn matrix of the computed centroids and idx, a m x 1 
%   vector of centroid assignments (i.e. each entry in range [1..K])
%
1
2
3
4
5
6
7
8
9
10
11
12
13
14

% Set default value for plot progress
if ~exist(‘plot_progress’, ‘var’) || isempty(plot_progress)
plot_progress = false;
end

% Plot the data if we are plotting progress
if plot_progress
figure;
hold on;
end

% Initialize values
[m n] = size(X);
K = size(initial_centroids, 1);
centroids = initial_centroids;
previous_centroids = centroids;
idx = zeros(m, 1);

% Run K-Means
for i=1:max_iters

% Output progress
fprintf('K-Means iteration %d/%d...\n', i, max_iters);
if exist('OCTAVE_VERSION')
    fflush(stdout);
end

% For each example in X, assign it to the closest centroid
idx = findClosestCentroids(X, centroids);

% Optionally, plot progress here
if plot_progress
    plotProgresskMeans(X, centroids, previous_centroids, idx, K, i);
    previous_centroids = centroids;
    fprintf('Press enter to continue.\n');
    pause;
end

% Given the memberships, compute new centroids
centroids = computeCentroids(X, idx, K);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

end

% Hold off if we are plotting progress
if plot_progress
hold off;
end

end

算法优化

代价函数（Distortion function）

要是k-means最后的分类结果最好，也就是要是K-均值最小化，是要最小化所有的数据点与其所关联的聚类中心点之间的距离之和，因此我们可以设计 K-均值的代价函数（又称 畸变函数 Distortion function）为：

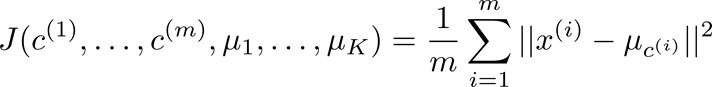
其中μ c (i)代表与 x (i) 最近的聚类中心点。 我们的的优化目标也就是要找出使得代价函数最小的 c (1) ,c (2) ,…,c (m) 和μ 1 ,μ 2 ,…,μ k 。
我们再回顾一下刚才给出的 K-means算法的迭代过程，我们知道，第一个步骤（根据聚类中心分类）是用于减小 c (i) 引起的代价，而第二个步骤（重新定位聚类中心）则是用于减小μ i 引起的代价。所以迭代的过程一定会是每一次迭代都在减小代价函数，如果发生迭代之后代价函数反而增加，则很可能是出现了错误。

如何选取k值

对于一个给定没有分类的数据集，最后具体应该分为多少类呢？这确实是一个问题，比如我们前面的那个例子，通过人眼观察，很明显可以分为两类，那么我们选取K值为2，可以得到一个比较好的聚类结果。那如果K选择3或者其他值行不行呢？当然也可以。
比如下图，有一个数据经过统计之后发现随着K值的增加其畸变函数在不断变小，但是我们发现在k=3时，畸变函数随着k值变化的幅度显著降低，在k>3之后所带来的好处并不是特别明显，所以我们可以选择k=3作为我们的聚类数目。由于其形状像我们人类的肘部，我们也称其为“肘部法则”。

但是实际应用中，k值的变换规律都不是和上图一样存在突变点，多数情况如下图所示：

随着k值的增大，其畸变函数也随着不断减小，根本就不存在明显的拐点。那么这种情况，K值的选择主要还是根据经验以及利用k-means聚类的目的来决定。

聚类中心的初始化

前面提到代价函数的建立，可以方便我们来对k-means算法的结果进行优化，方便我们察觉出算法迭代过程中的收敛问题，是否达到局部最小化，或者检查算法迭代过程中是否出现问题。而通过k值的选取也可能使我们的代价函数尽量的减小，以得到更好的聚类效果。
那么还有什么其他优化的方法呢？
我们还可以通过选取更优的聚类中心来优化聚类效果。
上面的例图是一个简单的二分类问题，并且不同类之间的界限也比较明显，最后我们得到的聚类结果也相对比较理想。但实际上聚类中心选择的不同，最终的聚类结果肯定也是会不一样的。
比如对于下面这张图：

我把初始的聚类中心选择在这两个不同的位置，最后导致的分类结果和迭代次数都会不一样。聚类中心的选取主要还是以随机为主，并且初始的时候最好是选择数据中的点。
对于多分类，甚至还会出现下面这种情况：


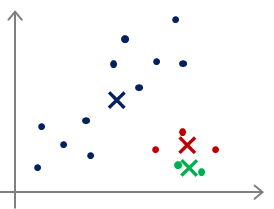
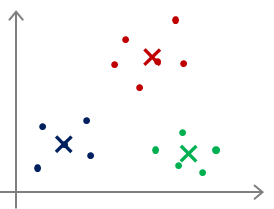
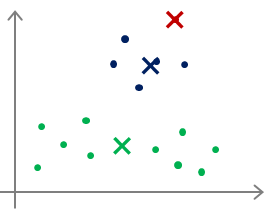
最后很可能仅仅实现了局部最优，把本来不是一类的多个类分为了一类，或者把本来是一类的分成了多个类，这些都是有可能的。那么对于这种情况怎么办呢？
对于聚类数目K值较小（K<10）的情况下，我们可以多次随机选取不同聚类中心，最后比较各自迭代完成后的畸变函数值，畸变函数越小，则说明聚类效果更优。但是在k值较大的情况下，比如上百类甚至上千万类，这时候重新选取不同的聚类中心可能就没有很好的效果了。