devbox
羊村懒王
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

神经网络系列---常用梯度下降算法

作者：羊村懒王 | 2024-02-26 06:49:33

赞

踩

神经网络系列---常用梯度下降算法

文章目录

常用梯度下降算法

当涉及不同的梯度下降算法时，每种算法都有其独特的特点和优化策略。下面对每种算法进行详细解释：

随机梯度下降（Stochastic Gradient Descent，SGD）：

  • 算法原理：在每次迭代中，随机选择一个训练样本来计算损失函数的梯度，并更新模型的参数。由于随机选择样本，梯度估计存在一定的噪声，导致优化路径不稳定，但收敛速度较快。

  • 优点：收敛速度快，计算开销较小。

  • 缺点：优化路径不稳定，可能会震荡，难以找到全局最优解。

  • 算法原理：在每次迭代中，使用所有训练样本来计算损失函数的梯度，并更新模型的参数。由于使用了更多数据，梯度估计更准确，收敛路径较稳定。

  • 优点：收敛路径稳定，梯度估计准确。

  • 缺点：计算开销较大，内存要求高，不适用于大规模数据集。

以下是随机梯度下降的详细解释：

  1. 算法原理：

    • 对于一个样本的训练数据 (x, y)，其中 x 是输入特征，y 是对应的实际标签。
    • SGD通过计算损失函数关于该样本的梯度来更新参数。梯度表示损失函数在每个参数处的变化率，它指示了在当前参数值下增加或减少参数值将如何影响损失函数的值。
    • SGD更新参数的规则为：新的参数 = 旧的参数 - 学习率 * 损失函数关于该样本的梯度。
    • 通过不断地使用不同的样本，迭代训练直至达到预定的训练轮数或损失函数收敛到一个满意的程度。

  2. 优点：

    • 计算开销小：由于每次迭代只使用一个样本，计算梯度的代价较小，特别适用于大规模数据集。
    • 更新频率高：参数的更新频率高，使得算法可能在较少的迭代次数内找到一个相对较好的解。

  3. 缺点：

    • 不稳定性：由于随机性，每次迭代的参数更新可能不同，导致优化路径不稳定，甚至可能出现震荡的情况。
    • 收敛性较慢：由于随机性导致的不稳定性，可能会导致收敛速度较慢，尤其是在损失函数存在大的震荡时。

  4. 改进方法：

    • 学习率调整：由于SGD的不稳定性，通常会使用学习率衰减技术来逐渐减小学习率，使得在训练初期更快收敛，后期细调参数。
    • Mini-batch：SGD的随机性使其不稳定，为了兼顾计算效率和稳定性，通常采用小批量梯度下降（Mini-batch Gradient Descent），在每次迭代中使用一小批样本来计算梯度。
    • Momentum：引入动量项，有助于加速优化过程，减少震荡。
随机梯度下降数学公式：

假设我们有一个损失函数 J ( θ ) J(θ) J(θ)（参数 θ θ θ表示模型的权重和偏置），其中 θ θ θ是一个向量。我们希望找到使损失函数最小化的最优参数 θ ∗ θ* θ∗。

  1. 损失函数： J ( θ ) J(θ) J(θ)

  2. 随机梯度下降公式：
    在随机梯度下降中，我们使用一个样本 ( x , y ) (x, y) (x,y) 来计算损失函数关于该样本的梯度，并更新参数。梯度表示损失函数在参数 θ θ θ处的变化率。

    损失函数关于参数 θ θ θ的梯度（梯度向量）： ∇ J ( θ ) = [ ∂ J ( θ ) / ∂ θ 1 , ∂ J ( θ ) / ∂ θ 2 , . . . , ∂ J ( θ ) / ∂ θ r ] ∇J(θ) = [∂J(θ)/∂θ₁, ∂J(θ)/∂θ₂, ..., ∂J(θ)/∂θᵣ] ∇J(θ)=[∂J(θ)/∂θ1​,∂J(θ)/∂θ2​,...,∂J(θ)/∂θr​]

    参数更新规则（学习率为α）：
    θ ← θ − α ∗ ∇ J ( θ ) θ ← θ - α * ∇J(θ) θ←θ−α∗∇J(θ)

代码演示
#include <iostream>
#include <vector>
#include <cmath>

// 随机梯度下降函数
void stochasticGradientDescent(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                               std::vector<double>& weights, double learning_rate, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    for (int epoch = 0; epoch < epochs; epoch++) {
        for (int i = 0; i < num_samples; i++) {
            double y_pred = predict(data[i], weights);
            double loss = lossFunction(y_pred, labels[i]);

            // 更新每个权重
            for (int j = 0; j < num_features; j++) {
                double gradient = (y_pred - labels[i]) * data[i][j];
                weights[j] -= learning_rate * gradient;
            }
        }
    }
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24

批量梯度下降（Batch Gradient Descent）

批量梯度下降（Batch Gradient Descent）是梯度下降算法的一种变体，在每次迭代中使用所有训练样本来计算损失函数关于参数的梯度，并更新模型的参数。与随机梯度下降（SGD）和小批量梯度下降（Mini-batch Gradient Descent）不同，它在每次迭代中使用全部训练样本，因此在计算梯度时具有更好的稳定性和准确性。

以下是批量梯度下降的详细解释：

  1. 算法原理：

    • 假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。
    • 在每次迭代中，使用所有训练样本计算损失函数关于参数θ的梯度。批量梯度下降会遍历所有样本，计算梯度的平均值。
    • 梯度表示损失函数在每个参数处的变化率。通过计算梯度，我们可以确定在当前参数值下，增加或减少参数值将如何影响损失函数的值。
    • 参数更新规则：新的参数 = 旧的参数 - 学习率 * (1 / 批大小) * ∑(损失函数关于所有样本的梯度)

  2. 优点：

    • 稳定性：由于使用所有样本的梯度，批量梯度下降的梯度估计更稳定，通常能够更准确地朝向损失函数的最小值方向移动。
    • 全局最优：相比随机梯度下降，批量梯度下降更有可能收敛到全局最优解，尤其是在凸优化问题中。

  3. 缺点：

    • 计算开销较大：由于每次迭代需要使用所有样本来计算梯度，批量梯度下降的计算开销较大。特别是在大规模数据集上，计算可能非常耗时。

  4. 改进方法：

    • 学习率调整：为了避免学习率过大或过小导致的优化问题，可以使用学习率衰减技术逐渐减小学习率，以便在训练初期更快收敛，后期更细调参数。
    • 随机梯度下降（SGD）和小批量梯度下降（Mini-batch Gradient Descent）：批量梯度下降在大规模数据集上的计算开销较大，为了加速优化过程，可以采用随机梯度下降或小批量梯度下降等变体。
批量梯度下降数学公式：

假设我们有一个损失函数 J ( θ ) J(θ) J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数 θ ∗ θ* θ∗。

  1. 损失函数： J ( θ ) J(θ) J(θ)

  2. 批量梯度下降公式：
    在批量梯度下降中，我们使用所有训练样本来计算损失函数关于参数θ的梯度，并更新模型的参数。

    损失函数关于参数θ的梯度（梯度向量）： ∇ J ( θ ) = [ ∂ J ( θ ) / ∂ θ 1 , ∂ J ( θ ) / ∂ θ 2 , . . . , ∂ J ( θ ) / ∂ θ r ] ∇J(θ) = [∂J(θ)/∂θ₁, ∂J(θ)/∂θ₂, ..., ∂J(θ)/∂θᵣ] ∇J(θ)=[∂J(θ)/∂θ1​,∂J(θ)/∂θ2​,...,∂J(θ)/∂θr​]

    参数更新规则（学习率为α）：
    θ ← θ − α ∗ ( 1 / 批大小 ) ∗ ∑ ( ∇ J ( θ ) ) θ ← θ - α * (1 / 批大小) * ∑(∇J(θ)) θ←θ−α∗(1/批大小)∗∑(∇J(θ))

其中∇表示梯度运算符，α是学习率（learning rate），r是参数的数量，批大小是在每次迭代中使用的样本数量。

代码演示
#include <iostream>
#include <vector>
#include <cmath>

// 批量梯度下降函数
void batchGradientDescent(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                          std::vector<double>& weights, double learning_rate, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    for (int epoch = 0; epoch < epochs; epoch++) {
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);

        // 初始化梯度
        std::vector<double> gradient(num_features, 0.0);

        // 计算梯度
        for (int i = 0; i < num_samples; i++) {
            for (int j = 0; j < num_features; j++) {
                gradient[j] += (y_pred[i] - labels[i]) * data[i][j];
            }
        }

        // 更新每个权重
        for (int j = 0; j < num_features; j++) {
            weights[j] -= learning_rate * (1.0 / num_samples) * gradient[j];
        }

        // 输出每次迭代的损失
        std::cout << "Epoch " << epoch + 1 << ", Loss: " << loss << std::endl;
    }
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34

小批量梯度下降（Mini-batch Gradient Descent）：

  • 算法原理：在每次迭代中，随机选择一小批训练样本来计算损失函数的梯度，并更新模型的参数。小批量梯度下降是批量梯度下降和随机梯度下降的折中方案。
  • 优点：收敛速度较快，梯度估计相对稳定，适用于大规模数据集。
  • 缺点：仍然可能会受到一定的优化路径波动影响。

小批量梯度下降（Mini-batch Gradient Descent）是梯度下降算法的一种改进版本，它是批量梯度下降和随机梯度下降的折中方案。在每次迭代中，小批量梯度下降使用一小批（通常为 2 的幂次 2的幂次 2的幂次）训练样本来计算损失函数关于参数的梯度，并更新模型的参数。相比于批量梯度下降，它在计算梯度时具有更好的效率，而相比于随机梯度下降，它的梯度估计更稳定，从而更容易收敛到较好的解。

以下是小批量梯度下降的详细解释：

  1. 算法原理：

    • 假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。
    • 在每次迭代中，选择一小批（通常为2的幂次）训练样本，计算损失函数关于该批样本的梯度。小批量梯度下降会遍历整个训练集，但每次迭代只使用一小批样本。
    • 梯度表示损失函数在每个参数处的变化率。通过计算梯度，我们可以确定在当前参数值下，增加或减少参数值将如何影响损失函数的值。
    • 参数更新规则：新的参数 = 旧的参数 - 学习率 * (1 / 批大小) * ∑(损失函数关于该批样本的梯度)

  2. 优点：

    • 计算效率高：相比于批量梯度下降，小批量梯度下降的计算开销较小，尤其适用于大规模数据集。
    • 梯度估计稳定：相比于随机梯度下降，小批量梯度下降使用一小批样本计算梯度，因此梯度估计更稳定，更容易收敛到较好的解。

  3. 缺点：

    • 超参数选择：小批量梯度下降中需要选择合适的批大小，这是一个超参数，不同的批大小可能会对优化过程产生影响。

  4. 改进方法：

    • 学习率调整：为了避免学习率过大或过小导致的优化问题，可以使用学习率衰减技术逐渐减小学习率，以便在训练初期更快收敛，后期更细调参数。
小批量梯度下降数学公式：

假设我们有一个损失函数 J ( θ ) J(θ) J(θ)（参数θ表示模型的权重和偏置），其中 θ θ θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数 θ ∗ θ* θ∗。

  1. 损失函数： J ( θ ) J(θ) J(θ)

  2. 小批量梯度下降公式：
    在小批量梯度下降中，我们使用一小批（通常为2的幂次）训练样本来计算损失函数关于参数θ的梯度，并更新模型的参数。

    损失函数关于参数θ的梯度（梯度向量）： ∇ J ( θ ) = [ ∂ J ( θ ) / ∂ θ 1 , ∂ J ( θ ) / ∂ θ 2 , . . . , ∂ J ( θ ) / ∂ θ r ] ∇J(θ) = [∂J(θ)/∂θ₁, ∂J(θ)/∂θ₂, ..., ∂J(θ)/∂θᵣ] ∇J(θ)=[∂J(θ)/∂θ1​,∂J(θ)/∂θ2​,...,∂J(θ)/∂θr​]

    参数更新规则（学习率为α，批大小为b）：
    θ ← θ − α ∗ ( 1 / b ) ∗ ∑ ( ∇ J ( θ ) ) θ ← θ - α * (1 / b) * ∑(∇J(θ)) θ←θ−α∗(1/b)∗∑(∇J(θ))

其中∇表示梯度运算符，α是学习率（learning rate），r是参数的数量，b是小批量的大小。

代码演示
#include <iostream>
#include <vector>
#include <cmath>

// 小批量梯度下降函数
void miniBatchGradientDescent(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                              std::vector<double>& weights, double learning_rate, int batch_size, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    for (int epoch = 0; epoch < epochs; epoch++) {
        for (int i = 0; i < num_samples; i += batch_size) {
            int end_idx = std::min(i + batch_size, num_samples);

            std::vector<double> batch_labels(labels.begin() + i, labels.begin() + end_idx);
            std::vector<std::vector<double>> batch_data(data.begin() + i, data.begin() + end_idx);

            std::vector<double> y_pred = predict(batch_data, weights);
            double loss = lossFunction(y_pred, batch_labels);

            // 初始化梯度
            std::vector<double> gradient(num_features, 0.0);

            // 计算梯度
            for (int j = 0; j < batch_size; j++) {
                for (int k = 0; k < num_features; k++) {
                    gradient[k] += (y_pred[j] - batch_labels[j]) * batch_data[j][k];
                }
            }

            // 更新每个权重
            for (int j = 0; j < num_features; j++) {
                weights[j] -= learning_rate * (1.0 / batch_size) * gradient[j];
            }
        }

        // 输出每次迭代的损失
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);
        std::cout << "Epoch " << epoch + 1 << ", Loss: " << loss << std::endl;
    }
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43

动量优化（Momentum Optimization）：

  • 算法原理：引入动量项来加速梯度下降过程。动量项利用参数更新的历史梯度信息来决定下一步的方向，从而增加了在参数空间中的“动量”，有助于快速穿越平坦区域和避免震荡。
  • 优点：加速收敛过程，减少震荡，有助于逃离局部最优解。
  • 缺点：可能会在某些情况下引入一定的摩擦，导致收敛变慢。

动量优化（Momentum Optimization）是一种梯度下降算法的改进版本，它通过模拟物体在惯性作用下的运动来加速收敛，并且有助于在梯度更新时减少震荡。动量优化可以在训练过程中更快地达到收敛，并且在复杂的非凸优化问题中通常表现较好。

动量优化算法的核心思想是在更新参数时，利用之前的梯度信息来为当前的梯度方向提供一个“动量”。这样做可以在梯度在一个方向上连续增大或减小时，使得参数更新更加平滑，从而加快收敛速度。

以下是动量优化算法的详细解释：

  1. 算法原理：

    • 假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。
    • 在每次迭代中，利用当前梯度和之前的动量来计算参数的更新量。
    • 动量的引入类似于模拟物体在运动过程中的惯性。在更新参数时，当前梯度方向上的更新将受到之前动量方向的影响。
    • 参数更新规则：新的参数 = 旧的参数 - 学习率 * 动量 * (上一次动量方向 + 当前梯度方向)

  2. 动量的计算：
    动量的计算类似于梯度的累积。我们引入一个动量系数β（通常取值为0.9或0.99），并维护一个动量向量v，初始化为0。在每次迭代中，根据当前梯度计算动量，并更新动量向量v。然后，用动量向量v来更新参数。

  3. 优点：

    • 收敛速度快：动量优化可以在训练过程中更快地达到收敛，尤其在高维、复杂的非凸优化问题中表现较好。
    • 减少震荡：动量的引入可以减少参数更新时的震荡，使得参数更新更加平滑。

  4. 超参数选择：

    • 学习率：动量优化算法依然需要选择适当的学习率，较大的学习率可能导致振荡，较小的学习率可能导致收敛缓慢。
    • 动量系数β：通常情况下，β取 0.9 0.9 0.9或 0.99 0.99 0.99是一个合理的选择，较大的β可以增加动量的影响。
动量优化数学公式：

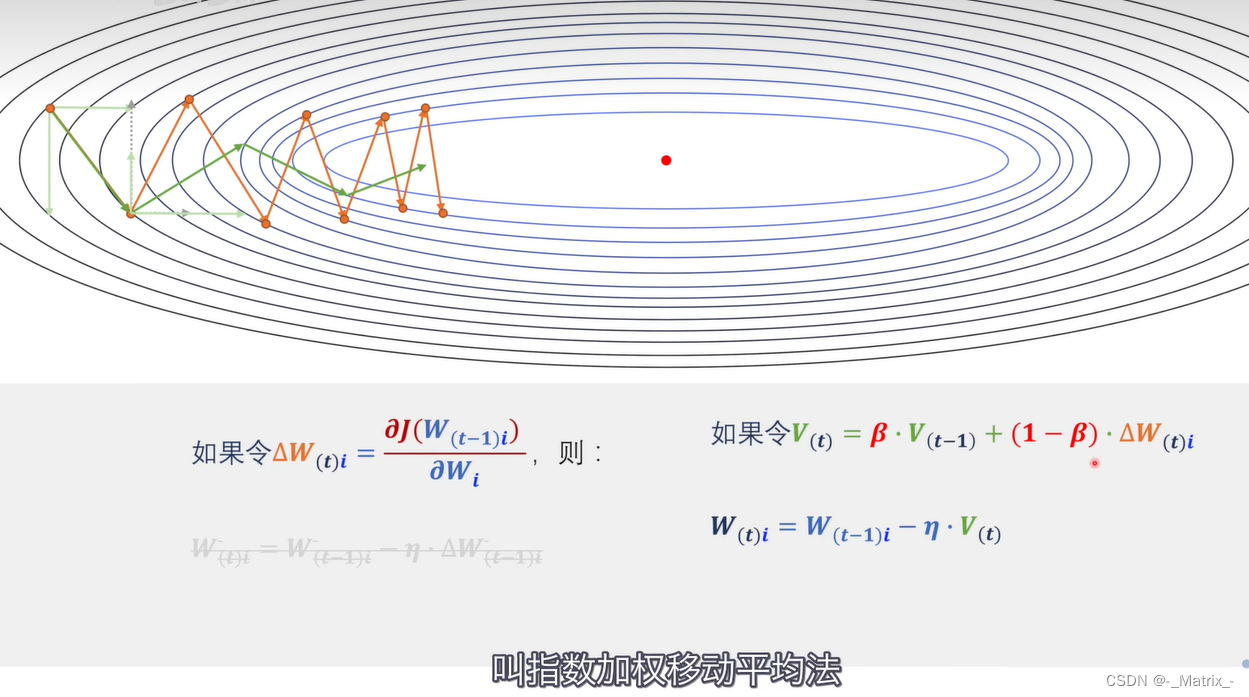
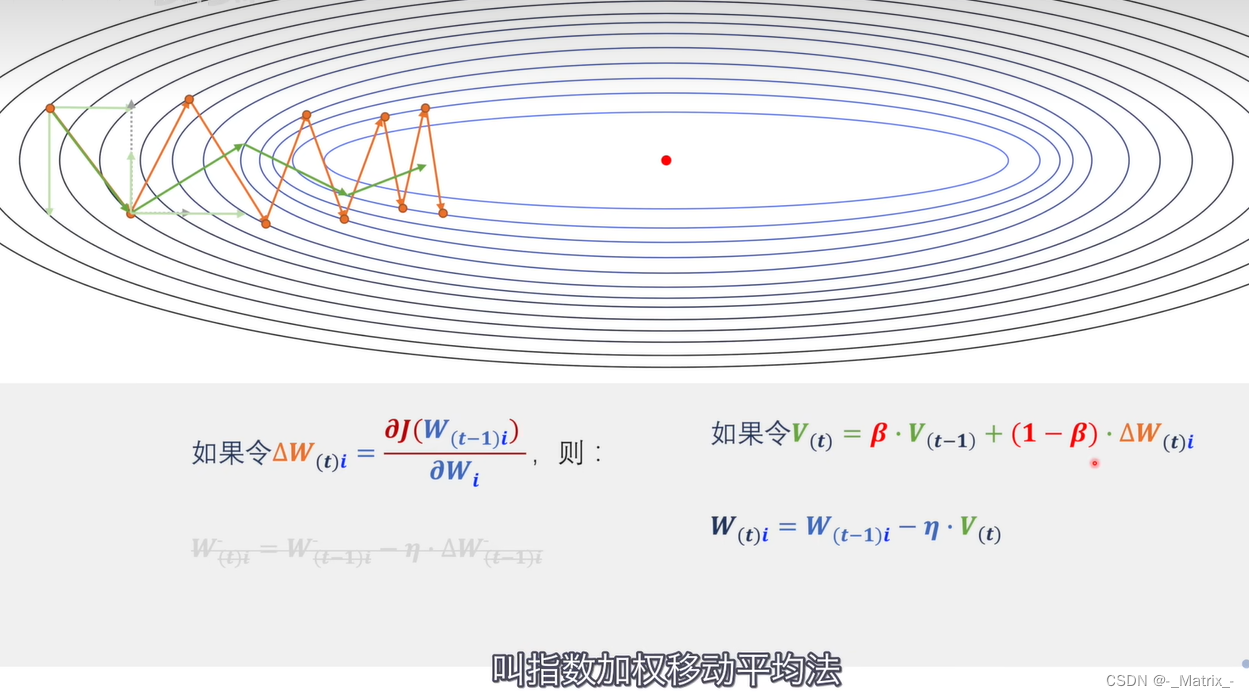
在这里插入图片描述

在这里插入图片描述

假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。

  1. 损失函数： J ( θ ) J(θ) J(θ)

  2. 动量向量的初始化：
    初始化动量向量 v = 0 v = 0 v=0，v的维度与θ相同。

  3. 动量的计算：
    在每次迭代中，利用当前梯度和之前的动量来计算动量。

    动量系数：β（通常取值为0.9或0.99）

    更新动量向量： v = β ∗ v + ( 1 − β ) ∗ ∇ J ( θ ) v = β * v + (1 - β) * ∇J(θ) v=β∗v+(1−β)∗∇J(θ)

    其中， ∇ J ( θ ) ∇J(θ) ∇J(θ)是损失函数关于参数θ的梯度（梯度向量）。

  4. 参数更新规则：
    使用动量向量v来更新参数θ。

    学习率： α α α

    参数更新： θ ← θ − α ∗ v θ ← θ - α * v θ←θ−α∗v

在每次迭代中，我们计算梯度 ∇ J ( θ ) ∇J(θ) ∇J(θ)并更新动量向量 v v v，然后使用动量向量 v v v来更新参数 θ θ θ。动量向量v模拟了之前梯度的“动量”，在梯度的方向上引入了惯性，使得参数更新更加平滑，从而加快收敛速度。

添加正则化 实例

当然！下面是在使用动量和L2正则化的参数更新中的具体数学公式。

首先，我们有L2正则化项的梯度：
∇ R ( θ ) = 2 λ θ \nabla R(\theta) = 2 \lambda \theta ∇R(θ)=2λθ

其中， λ \lambda λ是正则化强度。

然后，我们计算总梯度，该总梯度包括损失函数的梯度 ∇ J ( θ ) \nabla J(\theta) ∇J(θ)和正则化项的梯度：
totalGradient = ∇ J ( θ ) + ∇ R ( θ ) \text{totalGradient} = \nabla J(\theta) + \nabla R(\theta) totalGradient=∇J(θ)+∇R(θ)

接下来，我们根据以下公式计算动量向量 v v v：
v = β v + ( 1 − β ) totalGradient v = \beta v + (1 - \beta) \text{totalGradient} v=βv+(1−β)totalGradient

其中， β \beta β 是动量系数。

最后，我们使用学习率 α \alpha α 和动量向量 v v v来更新参数 θ \theta θ：
θ ← θ − α v \theta \leftarrow \theta - \alpha v θ←θ−αv

这样，我们就将动量和L2正则化结合在了同一优化步骤中。这两个技术通常用于更快地训练神经网络，以及减少过拟合。

代码演示
#include <iostream>
#include <vector>
#include <cmath>

// 动量优化函数
void momentumOptimization(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                          std::vector<double>& weights, double learning_rate, double beta, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    std::vector<double> velocity(num_features, 0.0);

    for (int epoch = 0; epoch < epochs; epoch++) {
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);

        // 初始化梯度
        std::vector<double> gradient(num_features, 0.0);

        // 计算梯度
        for (int i = 0; i < num_samples; i++) {
            for (int j = 0; j < num_features; j++) {
                gradient[j] += (y_pred[i] - labels[i]) * data[i][j];
            }
        }

        // 更新动量
        for (int j = 0; j < num_features; j++) {
            velocity[j] = beta * velocity[j] + (1 - beta) * gradient[j];
        }

        // 更新每个权重
        for (int j = 0; j < num_features; j++) {
            weights[j] -= learning_rate * velocity[j];
        }

        // 输出每次迭代的损失
        std::cout << "Epoch " << epoch + 1 << ", Loss: " << loss << std::endl;
    }
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41

Adagrad（Adaptive Gradient Algorithm）：

  • 算法原理：Adagrad是一种自适应学习率的优化算法。它为每个参数使用不同的学习率，根据每个参数的历史梯度信息来自适应地调整学习率。较大梯度参数的学习率逐渐减小，较小梯度参数的学习率逐渐增大。
  • 优点：自适应学习率，适应不同参数的更新需求。
  • 缺点：学习率可能过早减小，导致收敛速度过慢。

Adagrad（Adaptive Gradient Algorithm）是一种自适应学习率的梯度下降算法，它可以针对每个参数自适应地调整学习率，从而更有效地优化模型。Adagrad的主要思想是在训练过程中为每个参数维护一个学习率，根据参数的历史梯度信息来自适应地调整学习率大小。

以下是Adagrad算法的详细解释：

  1. 算法原理：

    • 假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。
    • Adagrad算法为每个参数θ维护一个累积梯度平方和（sum of squared gradients），并使用该平方和来调整参数的学习率。
    • 参数更新规则：对于第t次迭代，学习率为α，θ在第t+1次迭代的更新公式为：
      θ(t+1) ← θ(t) - (α / sqrt(G(t) + ε)) * ∇J(θ(t))

    其中∇J(θ(t))是损失函数关于参数θ在第t次迭代的梯度，G(t)是累积梯度平方和，ε是一个小的常数（通常取较小的值，例如1e-8）以防止除以0。

  2. 累积梯度平方和的计算：
    在每次迭代中，对参数的梯度进行平方，然后将平方梯度值加到之前的累积梯度平方和中。

  3. 优点：

    • 自适应学习率：Adagrad根据参数的历史梯度信息自适应地调整学习率，较大梯度对应的参数学习率较小，较小梯度对应的参数学习率较大，使得参数的学习过程更加平稳。
    • 对于稀疏特征优化较好：Adagrad在处理稀疏特征时相对于其他算法更具优势。

  4. 缺点：

    • 累积梯度平方和：由于Adagrad累积梯度平方和，对于长时间训练的模型，梯度平方和会变得较大，导致学习率过度减小，可能导致训练过早停止。

  5. 改进方法：

    • 学习率调整：由于累积梯度平方和会变大，可以使用学习率衰减技术逐渐减小学习率，以便在训练过程中更细调参数。
Adagrad数学公式：

在这里插入图片描述

假设我们有一个损失函数 J ( θ ) J(θ) J(θ)（参数θ表示模型的权重和偏置），其中 θ θ θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数 θ ∗ θ* θ∗。

  1. 损失函数： J ( θ ) J(θ) J(θ)

  2. 学习率： α α α

  3. Adagrad的参数更新规则：
    Adagrad算法为每个参数θ维护一个累积梯度平方和（sum of squared gradients），并使用该平方和来调整参数的学习率。

    在第t次迭代时，我们计算参数θ的梯度∇J(θ(t))，并将其平方进行累加：
    G ( t ) = G ( t − 1 ) + ( ∇ J ( θ ( t ) ) ) 2 G(t) = G(t-1) + (∇J(θ(t)))^2 G(t)=G(t−1)+(∇J(θ(t)))2

    然后，使用累积梯度平方和G(t)来更新参数θ：
    θ ( t + 1 ) = θ ( t ) − ( α / s q r t ( G ( t ) + ε ) ) ∗ ∇ J ( θ ( t ) ) θ(t+1) = θ(t) - (α / sqrt(G(t) + ε)) * ∇J(θ(t)) θ(t+1)=θ(t)−(α/sqrt(G(t)+ε))∗∇J(θ(t))

    其中：

    • ∇J(θ(t))是损失函数关于参数θ在第t次迭代的梯度（梯度向量）。
    • G(t)是累积梯度平方和，它维护了参数θ每个维度梯度的累积平方和。
    • ε是一个小的常数，通常取较小的值（例如1e-8）以防止除以0。
添加正则化 实例

正则化通常通过在损失函数中添加一个与模型参数的大小有关的项来实现。对于L1或L2正则化，这个额外的项会考虑参数的绝对值或平方值。对于你提供的优化器公式，添加正则化需要考虑正则化项对梯度的影响。

以L2正则化为例，L2正则化项与参数的平方成正比，因此其对梯度的贡献是线性的。假设正则化强度为 λ \lambda λ，我们可以将L2正则化项的梯度表示为 2 λ θ ( t ) 2\lambda\theta(t) 2λθ(t)。

因此，损失函数的梯度将变为：

KaTeX parse error: {align*} can be used only in display mode.

然后，我们可以将这个新的梯度插入到原始的优化器更新公式中：

KaTeX parse error: {align*} can be used only in display mode.

其中

  • θ ( t ) \theta(t) θ(t)是第(t)次迭代的参数。
  • α \alpha α是学习率。
  • G ( t ) G(t) G(t)是累积梯度平方和。
  • ϵ \epsilon ϵ是一个小的常数，通常取较小的值以防止除以0。
  • ∇ J ( θ ( t ) ) \nabla J(\theta(t)) ∇J(θ(t))是原始损失函数关于参数 θ \theta θ在第 t t t次迭代的梯度。
  • λ \lambda λ是正则化强度对不起，我的之前的解释确实引入了混淆。为了澄清，让我们回顾一下具体的步骤。
代码演示
#include <iostream>
#include <vector>
#include <cmath>

// Adagrad优化函数
void adagradOptimization(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                         std::vector<double>& weights, double learning_rate, double epsilon, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    std::vector<double> sum_squared_gradients(num_features, 0.0);

    for (int epoch = 0; epoch < epochs; epoch++) {
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);

        // 初始化梯度
        std::vector<double> gradient(num_features, 0.0);

        // 计算梯度
        for (int i = 0; i < num_samples; i++) {
            for (int j = 0; j < num_features; j++) {
                gradient[j] += (y_pred[i] - labels[i]) * data[i][j];
            }
        }

        // 更新累积梯度平方和
        for (int j = 0; j < num_features; j++) {
            sum_squared_gradients[j] += gradient[j] * gradient[j];
        }

        // 更新每个权重
        for (int j = 0; j < num_features; j++) {
            weights[j] -= (learning_rate / (std::sqrt(sum_squared_gradients[j]) + epsilon)) * gradient[j];
        }

        // 输出每次迭代的损失
        std::cout << "Epoch " << epoch + 1 << ", Loss: " << loss << std::endl;
    }
}



  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42

RMSprop（Root Mean Square Propagation）：

  • 算法原理：RMSprop也是一种自适应学习率算法，类似于Adagrad，但采用了对梯度进行指数加权平均，以便更快地遗忘旧的梯度信息。这样，它在一定程度上解决了Adagrad的学习率过早减小的问题。
  • 优点：自适应学习率，对旧梯度有较好遗忘性。
  • 缺点：学习率衰减依然存在，可能在训练后期导致学习率过小。

RMSprop（Root Mean Square Propagation）是一种自适应学习率的梯度下降算法，它是Adagrad算法的一种改进版本。RMSprop通过引入一个衰减系数（decay rate）来解决Adagrad算法中累积梯度平方和过大导致学习率过度减小的问题。RMSprop在处理长时间训练的模型时表现更好，并且在深度学习中广泛应用。

以下是RMSprop算法的详细解释：

  1. 算法原理：

    • 假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。
    • RMSprop算法为每个参数θ维护一个累积梯度平方和（sum of squared gradients），并使用该平方和来调整参数的学习率。
    • 参数更新规则：对于第t次迭代，学习率为α，衰减系数为β，θ在第t+1次迭代的更新公式为：
      G ( t ) = β ∗ G ( t − 1 ) + ( 1 − β ) ∗ ( ∇ J ( θ ( t ) ) ) 2 G(t) = β * G(t-1) + (1 - β) * (∇J(θ(t)))^2 G(t)=β∗G(t−1)+(1−β)∗(∇J(θ(t)))2
      θ ( t + 1 ) = θ ( t ) − ( α / s q r t ( G ( t ) + ε ) ) ∗ ∇ J ( θ ( t ) ) θ(t+1) = θ(t) - (α / sqrt(G(t) + ε)) * ∇J(θ(t)) θ(t+1)=θ(t)−(α/sqrt(G(t)+ε))∗∇J(θ(t))

    其中：

    • ∇J(θ(t))是损失函数关于参数θ在第t次迭代的梯度（梯度向量）。
    • G(t)是累积梯度平方和，它维护了参数θ每个维度梯度的累积平方和。
    • β是衰减系数，通常取值为0.9，用于控制历史梯度平方和的衰减程度。
    • ε是一个小的常数，通常取较小的值（例如1e-8）以防止除以0。

  2. 优点：

    • 自适应学习率：RMSprop根据参数的历史梯度信息自适应地调整学习率，较大梯度对应的参数学习率较小，较小梯度对应的参数学习率较大，使得参数的学习过程更加平稳。
    • 衰减系数：RMSprop引入了衰减系数β，可以解决Adagrad算法中累积梯度平方和过大导致学习率过度减小的问题。

  3. 改进方法：

    • 学习率调整：可以使用学习率衰减技术逐渐减小学习率，以便在训练过程中更细调参数。
RMSprop数学公式：

假设我们有一个损失函数 J ( θ ) J(θ) J(θ)（参数θ表示模型的权重和偏置），其中 θ θ θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数 θ ∗ θ* θ∗。

  1. 损失函数： J ( θ ) J(θ) J(θ)

  2. 学习率： α α α

  3. 衰减系数： β β β

  4. RMSprop的参数更新规则：
    RMSprop算法为每个参数θ维护一个累积梯度平方和（sum of squared gradients），并使用该平方和来调整参数的学习率。

    在第t次迭代时，我们计算参数θ的梯度∇J(θ(t))，并将其平方进行累加，然后利用衰减系数β对累积梯度平方和进行衰减：
    G ( t ) = β ∗ G ( t − 1 ) + ( 1 − β ) ∗ ( ∇ J ( θ ( t ) ) ) 2 G(t) = β * G(t-1) + (1 - β) * (∇J(θ(t)))^2 G(t)=β∗G(t−1)+(1−β)∗(∇J(θ(t)))2

    然后，使用累积梯度平方和G(t)来更新参数θ：
    θ ( t + 1 ) = θ ( t ) − ( α / s q r t ( G ( t ) + ε ) ) ∗ ∇ J ( θ ( t ) ) θ(t+1) = θ(t) - (α / sqrt(G(t) + ε)) * ∇J(θ(t)) θ(t+1)=θ(t)−(α/sqrt(G(t)+ε))∗∇J(θ(t))

    其中：

    • ∇J(θ(t))是损失函数关于参数θ在第t次迭代的梯度（梯度向量）。
    • G(t)是累积梯度平方和，它维护了参数θ每个维度梯度的累积平方和。
    • β是衰减系数，通常取值为0.9，用于控制历史梯度平方和的衰减程度。
    • ε是一个小的常数，通常取较小的值（例如1e-8）以防止除以0。
代码演示
#include <iostream>
#include <vector>
#include <cmath>

// RMSprop优化函数
void rmspropOptimization(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                         std::vector<double>& weights, double learning_rate, double beta, double epsilon, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    std::vector<double> squared_gradients(num_features, 0.0);

    for (int epoch = 0; epoch < epochs; epoch++) {
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);

        // 初始化梯度
        std::vector<double> gradient(num_features, 0.0);

        // 计算梯度
        for (int i = 0; i < num_samples; i++) {
            for (int j = 0; j < num_features; j++) {
                gradient[j] += (y_pred[i] - labels[i]) * data[i][j];
            }
        }

        // 更新累积梯度平方和
        for (int j = 0; j < num_features; j++) {
            squared_gradients[j] = beta * squared_gradients[j] + (1 - beta) * gradient[j] * gradient[j];
        }

        // 更新每个权重
        for (int j = 0; j < num_features; j++) {
            weights[j] -= (learning_rate / (std::sqrt(squared_gradients[j]) + epsilon)) * gradient[j];
        }

        // 输出每次迭代的损失
        std::cout << "Epoch " << epoch + 1 << ", Loss: " << loss << std::endl;
    }
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41

Adam（Adaptive Moment Estimation）：

  • 算法原理：Adam是结合了动量优化和RMSprop的优势的自适应学习率算法。它利用梯度的一阶矩估计（平均梯度）和二阶矩估计（梯度的方差）来调整参数的更新步长，并结合动量项，使得参数更新更加平稳且具有自适应性。
  • 优点：自适应学习率，收敛速度快，对于不同参数具有较好的适应性。
  • 缺点：有一些超参数需要调整，计算开销较大。

以下是Adam算法的详细解释：

  1. 算法原理：

    • 假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。

    • Adam算法为每个参数θ维护两个一阶矩估计（first moment estimate）m和二阶矩估计（second moment estimate）v，并使用它们来调整参数的学习率。

    • 参数更新规则：对于第t次迭代，学习率为α，衰减系数为β1和β2，ε是一个小的常数（通常取较小的值，例如1e-8）以防止除以0，θ在第t+1次迭代的更新公式为：

      m ( t ) = β 1 ∗ m ( t − 1 ) + ( 1 − β 1 ) ∗ ∇ J ( θ ( t ) ) m(t) = β1 * m(t-1) + (1 - β1) * ∇J(θ(t)) m(t)=β1∗m(t−1)+(1−β1)∗∇J(θ(t)) （一阶矩估计）
      v ( t ) = β 2 ∗ v ( t − 1 ) + ( 1 − β 2 ) ∗ ( ∇ J ( θ ( t ) ) ) 2 v(t) = β2 * v(t-1) + (1 - β2) * (∇J(θ(t)))^2 v(t)=β2∗v(t−1)+(1−β2)∗(∇J(θ(t)))2 （二阶矩估计）

      m h a t ( t ) = m ( t ) / ( 1 − β 1 t ) m_hat(t) = m(t) / (1 - β1^t) mh​at(t)=m(t)/(1−β1t) （修正一阶矩估计）
      v h a t ( t ) = v ( t ) / ( 1 − β 2 t ) v_hat(t) = v(t) / (1 - β2^t) vh​at(t)=v(t)/(1−β2t) （修正二阶矩估计）

      θ ( t + 1 ) = θ ( t ) − ( α / ( s q r t ( v h a t ( t ) ) + ε ) ) ∗ m h a t ( t ) θ(t+1) = θ(t) - (α / (sqrt(v_hat(t)) + ε)) * m_hat(t) θ(t+1)=θ(t)−(α/(sqrt(vh​at(t))+ε))∗mh​at(t)

    其中：

    • ∇J(θ(t))是损失函数关于参数θ在第t次迭代的梯度（梯度向量）。
    • m(t)和v(t)分别表示一阶矩估计和二阶矩估计，它们初始化为0向量。
    • β1和β2是衰减系数，通常取值为0.9和0.999，分别用于控制一阶矩和二阶矩的衰减程度。
    • m_hat(t)和v_hat(t)是修正后的一阶矩估计和二阶矩估计，用于解决算法初期估计偏向0的问题。

  2. 优点：

    • 自适应学习率：Adam根据参数的一阶矩和二阶矩估计自适应地调整学习率，使得参数的学习过程更加平稳。
    • 鲁棒性：Adam对于稀疏梯度的处理较为优秀，使得算法在处理非平稳目标函数和大规模数据集时表现更好。

  3. 改进方法：

    • 学习率调整：可以使用学习率衰减技术逐渐减小学习率，以便在训练过程中更细调参数。
Adam数学公式：

假设我们有一个损失函数 J ( θ ) J(θ) J(θ)（参数θ表示模型的权重和偏置），其中 θ θ θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数 θ ∗ θ* θ∗。

  1. 损失函数： J ( θ ) J(θ) J(θ)

  2. 学习率： α α α

  3. 衰减系数： β 1 和 β 2 β1和β2 β1和β2

  4. 一阶矩估计（m）和二阶矩估计（v）：
    Adam算法为每个参数θ维护两个一阶矩估计和二阶矩估计，并使用它们来调整参数的学习率。

    在第t次迭代时，我们计算参数θ的梯度∇J(θ(t))，然后分别计算一阶矩估计m和二阶矩估计v：
    m ( t ) = β 1 ∗ m ( t − 1 ) + ( 1 − β 1 ) ∗ ∇ J ( θ ( t ) ) m(t) = β1 * m(t-1) + (1 - β1) * ∇J(θ(t)) m(t)=β1∗m(t−1)+(1−β1)∗∇J(θ(t))
    v ( t ) = β 2 ∗ v ( t − 1 ) + ( 1 − β 2 ) ∗ ( ∇ J ( θ ( t ) ) ) 2 v(t) = β2 * v(t-1) + (1 - β2) * (∇J(θ(t)))^2 v(t)=β2∗v(t−1)+(1−β2)∗(∇J(θ(t)))2

    其中：

    • ∇J(θ(t))是损失函数关于参数θ在第t次迭代的梯度（梯度向量）。
    • m(t)是一阶矩估计，它表示过去梯度的一阶矩（均值）。
    • v(t)是二阶矩估计，它表示过去梯度平方的二阶矩（平均平方）。
    • β1和β2是衰减系数，通常取值为0.9和0.999，分别用于控制一阶矩和二阶矩的衰减程度。

  5. 修正后的一阶矩估计（m_hat）和二阶矩估计（v_hat）：
    由于在算法初期估计偏向0，需要对一阶矩估计m和二阶矩估计v进行修正。

    m h a t ( t ) = m ( t ) / ( 1 − β 1 t ) m_hat(t) = m(t) / (1 - β1^t) mh​at(t)=m(t)/(1−β1t)
    v h a t ( t ) = v ( t ) / ( 1 − β 2 t ) v_hat(t) = v(t) / (1 - β2^t) vh​at(t)=v(t)/(1−β2t)

  6. 参数更新规则：
    使用修正后的一阶矩估计m_hat和二阶矩估计v_hat来更新参数θ。

    θ ( t + 1 ) = θ ( t ) − ( α / ( s q r t ( v h a t ( t ) ) + ε ) ) ∗ m h a t ( t ) θ(t+1) = θ(t) - (α / (sqrt(v_hat(t)) + ε)) * m_hat(t) θ(t+1)=θ(t)−(α/(sqrt(vh​at(t))+ε))∗mh​at(t)

    其中：

    • α是学习率，用于控制参数更新的步长。
    • ε是一个小的常数，通常取较小的值（例如1e-8）以防止除以0。
代码演示
#include <iostream>
#include <vector>
#include <cmath>

// Adam优化函数
void adamOptimization(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                      std::vector<double>& weights, double learning_rate, double beta1, double beta2, double epsilon, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    std::vector<double> m(num_features, 0.0); // 一阶矩估计
    std::vector<double> v(num_features, 0.0); // 二阶矩估计
    int t = 0; // 时间步数

    for (int epoch = 0; epoch < epochs; epoch++) {
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);

        // 初始化梯度
        std::vector<double> gradient(num_features, 0.0);

        // 计算梯度
        for (int i = 0; i < num_samples; i++) {
            for (int j = 0; j < num_features; j++) {
                gradient[j] += (y_pred[i] - labels[i]) * data[i][j];
            }
        }

        // 更新时间步数
        t++;

        // 更新一阶矩估计和二阶矩估计
        for (int j = 0; j < num_features; j++) {
            m[j] = beta1 * m[j] + (1 - beta1) * gradient[j];
            v[j] = beta2 * v[j] + (1 - beta2) * gradient[j] * gradient[j];
        }

        // 进行修正后的一阶矩估计和二阶矩估计
        std::vector<double> m_hat(num_features, 0.0);
        std::vector<double> v_hat(num_features, 0.0);
        for (int j = 0; j < num_features; j++) {
            m_hat[j] = m[j] / (1 - std::pow(beta1, t));
            v_hat[j] = v[j] / (1 - std::pow(beta2, t));
        }

        // 更新每个权重
        for (int j = 0; j < num_features; j++) {
            weights[j] -= (learning_rate / (std::sqrt(v_hat[j]) + epsilon)) * m_hat[j];
        }

        // 输出每次迭代的损失
        std::cout << "Epoch " << epoch + 1 << ", Loss: " << loss << std::endl;
    }
}


  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55

NAG （Nesterov Accelerated Gradient）

（Nesterov加速梯度法），简称NAG，是一种优化算法，用于训练神经网络和其他机器学习模型。Nesterov算法是梯度下降算法的一种变种，通过引入动量（momentum）的概念来加速收敛，并在损失函数梯度的计算中采用"look-ahead"策略来调整参数的更新方向，从而在训练过程中减少震荡和摆动。

Nesterov算法的特点在于在计算梯度时先对参数进行一次"look-ahead"更新，然后在该位置上计算梯度。这使得梯度计算的方向更加准确，能够更好地适应参数的变化情况。

以下是Nesterov算法的详细解释：

  1. 算法原理：

    • 假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。

    • Nesterov算法引入了动量（momentum）的概念。动量是过去梯度的加权平均，它在梯度的计算中增加了一个惯性项，从而加速收敛。

    • 参数更新规则：对于第t次迭代，学习率为α，动量系数为γ，参数θ的一阶梯度为∇J(θ)。

      v ( t ) = γ ∗ v ( t − 1 ) + α ∗ ∇ J ( θ − γ ∗ v ( t − 1 ) ) v(t) = γ * v(t-1) + α * ∇J(θ - γ * v(t-1)) v(t)=γ∗v(t−1)+α∗∇J(θ−γ∗v(t−1)) （计算动量）
      θ ( t + 1 ) = θ ( t ) − v ( t ) θ(t+1) = θ(t) - v(t) θ(t+1)=θ(t)−v(t) （更新参数）

    其中：

    • v(t)是动量的累积向量，它代表过去梯度的加权平均。
    • γ是动量系数，通常取值范围为0到1之间，用于控制动量的权重。较大的γ值会增加惯性，使得更新更加平滑，但可能导致震荡；较小的γ值会减小惯性，使得更新更加准确，但可能导致更新速度较慢。

  2. 优点：

    • 收敛加速：动量的引入使得参数更新更加平滑，从而加速收敛过程。
    • 减少震荡：Nesterov算法通过"look-ahead"策略调整参数的更新方向，减少了梯度下降过程中的震荡和摆动。

  3. 改进方法：

    • 学习率调整：可以使用学习率衰减技术逐渐减小学习率，以便在训练过程中更细调参数。
Nesterov加速梯度法数学公式：

假设我们有一个损失函数 J ( θ ) J(θ) J(θ)（参数θ表示模型的权重和偏置），其中 θ θ θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数 θ ∗ θ* θ∗。

  1. 损失函数： J ( θ ) J(θ) J(θ)

  2. 学习率： α α α

  3. 动量系数： γ γ γ

  4. 动量（momentum）的累积向量（v）：
    Nesterov算法引入了动量的概念，动量是过去梯度的加权平均。

    在第t次迭代时，我们首先进行动量的累积，然后计算梯度：
    v ( t ) = γ ∗ v ( t − 1 ) + α ∗ ∇ J ( θ − γ ∗ v ( t − 1 ) ) v(t) = γ * v(t-1) + α * ∇J(θ - γ * v(t-1)) v(t)=γ∗v(t−1)+α∗∇J(θ−γ∗v(t−1))

    其中：

    • v(t)是动量的累积向量，它代表过去梯度的加权平均。
    • γ是动量系数，通常取值范围为0到1之间，用于控制动量的权重。较大的γ值会增加惯性，使得更新更加平滑，但可能导致震荡；较小的γ值会减小惯性，使得更新更加准确，但可能导致更新速度较慢。

  5. 参数更新规则：
    使用动量的累积向量v来更新参数θ。

    θ ( t + 1 ) = θ ( t ) − v ( t ) θ(t+1) = θ(t) - v(t) θ(t+1)=θ(t)−v(t)

代码演示
#include <iostream>
#include <vector>
#include <cmath>


// 第一种写法-Nesterov算法优化函数
void nesterovOptimization(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                          std::vector<double>& weights, double learning_rate, double momentum, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    std::vector<double> v(num_features, 0.0); // 动量的累积向量

    for (int epoch = 0; epoch < epochs; epoch++) {
        // 提前计算"look-ahead"位置的参数更新
        std::vector<double> theta_ahead(num_features, 0.0);
        for (int j = 0; j < num_features; j++) {
            theta_ahead[j] = weights[j] - momentum * v[j];
        }

        // 计算"look-ahead"位置的梯度
        std::vector<double> gradient_ahead(num_features, 0.0);
        std::vector<double> y_pred_ahead = predict(data, theta_ahead);
        for (int i = 0; i < num_samples; i++) {
            for (int j = 0; j < num_features; j++) {
                gradient_ahead[j] += (y_pred_ahead[i] - labels[i]) * data[i][j];
            }
        }

        // 更新动量的累积向量
        for (int j = 0; j < num_features; j++) {
            v[j] = momentum * v[j] + learning_rate * gradient_ahead[j];
        }

        // 更新参数
        for (int j = 0; j < num_features; j++) {
            weights[j] -= v[j];
        }

        // 计算损失并输出
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);
        std::cout << "Epoch " << epoch + 1 << ", Loss: " << loss << std::endl;
    }
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
Nesterov第二种写法

在这里插入图片描述

在这里插入图片描述

代码演示2

//  第二种写法-Nesterov算法优化函数（推荐)
void nesterovOptimization(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                          std::vector<double>& weights, double learning_rate, double momentum, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    std::vector<double> v(num_features, 0.0); // 动量的累积向量

    for (int epoch = 0; epoch < epochs; epoch++) {
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);

        // 初始化梯度
        std::vector<double> gradient(num_features, 0.0);

        // 计算梯度
        for (int i = 0; i < num_samples; i++) {
            for (int j = 0; j < num_features; j++) {
                gradient[j] += (y_pred[i] - labels[i]) * data[i][j];
            }
        }

        // 更新动量的累积向量
        for (int j = 0; j < num_features; j++) {
            v[j] = momentum * v[j] + learning_rate * gradient_ahead[j];
        }

        // 更新参数
        for (int j = 0; j < num_features; j++) {
            weights[j] -= (momentum * v[j] + learning_rate * gradient_ahead[j]);
        }

        // 计算损失并输出
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);
        std::cout << "Epoch " << epoch + 1 << ", Loss: " << loss << std::endl;
    }
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39

Nadam（Nesterov-accelerated Adaptive Moment Estimation）

Nadam 是一种优化算法，结合了Nesterov Accelerated Gradient（NAG）和Adam两种优化算法的特点。Nadam在深度学习中广泛应用，是目前训练神经网络的优化算法之一。

Nadam算法在Adam的基础上进行了改进，主要是对Adam的动量部分进行了修改。Nadam的优点在于对于凸优化和非凸优化问题都具有较好的性能，并且对于稀疏梯度的处理也比较优秀。

以下是Nadam算法的详细解释：

  1. 算法原理：

    • 假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。

    • Nadam算法为每个参数θ维护两个一阶矩估计（first moment estimate）m和二阶矩估计（second moment estimate）v，并使用它们来调整参数的学习率。

    • 参数更新规则：对于第t次迭代，学习率为α，衰减系数为β1和β2，ε是一个小的常数（通常取较小的值，例如1e-8）以防止除以0，β1_t和β2_t是β1和β2的时间步数的衰减校正。

      m ( t ) = β 1 ∗ m ( t − 1 ) + ( 1 − β 1 ) ∗ ∇ J ( θ ( t ) ) m(t) = β1 * m(t-1) + (1 - β1) * ∇J(θ(t)) m(t)=β1∗m(t−1)+(1−β1)∗∇J(θ(t)) （一阶矩估计）
      v ( t ) = β 2 ∗ v ( t − 1 ) + ( 1 − β 2 ) ∗ ( ∇ J ( θ ( t ) ) ) 2 v(t) = β2 * v(t-1) + (1 - β2) * (∇J(θ(t)))^2 v(t)=β2∗v(t−1)+(1−β2)∗(∇J(θ(t)))2 （二阶矩估计）
      m h a t ( t ) = m ( t ) / ( 1 − β 1 t ) m_hat(t) = m(t) / (1 - β1^t) mh​at(t)=m(t)/(1−β1t) （修正一阶矩估计）
      v h a t ( t ) = v ( t ) / ( 1 − β 2 t ) v_hat(t) = v(t) / (1 - β2^t) vh​at(t)=v(t)/(1−β2t) （修正二阶矩估计）
      θ ( t + 1 ) = θ ( t ) − ( α / ( s q r t ( v h a t ( t ) ) + ε ) ) ∗ ( β 1 t ∗ m h a t ( t ) + ( 1 − β 1 t ) ∗ ∇ J ( θ ( t ) ) ) θ(t+1) = θ(t) - (α / (sqrt(v_hat(t)) + ε)) * (β1_t * m_hat(t) + (1 - β1_t) * ∇J(θ(t))) θ(t+1)=θ(t)−(α/(sqrt(vh​at(t))+ε))∗(β1t​∗mh​at(t)+(1−β1t​)∗∇J(θ(t)))

    其中：

    • ∇J(θ(t))是损失函数关于参数θ在第t次迭代的梯度（梯度向量）。
    • m(t)和v(t)分别表示一阶矩估计和二阶矩估计，它们初始化为0向量。
    • β1和β2是衰减系数，通常取值为0.9和0.999，分别用于控制一阶矩和二阶矩的衰减程度。
    • β1_t和β2_t是β1和β2的时间步数的衰减校正，它们用于修正动量的计算。
    • m_hat(t)和v_hat(t)是修正后的一阶矩估计和二阶矩估计，用于解决算法初期估计偏向0的问题。

  2. 优点：

    • 自适应学习率：Nadam根据参数的一阶矩和二阶矩估计自适应地调整学习率，使得参数的学习过程更加平稳。
    • 对凸优化和非凸优化都有效：Nadam在处理凸优化和非凸优化问题时都具有较好的性能。

  3. 改进方法：

    • 学习率调整：可以使用学习率衰减技术逐渐减小学习率，以便在训练过程中更细调参数。

Nadam算法在深度学习中广泛应用，特别适用于训练复杂的深度神经网络和处理大规模数据集。它是目前训练神经网络的优化算法之一，并且在很多实际任务中表现优秀。

Nadam算法数学公式：

假设我们有一个损失函数 J(θ)（参数θ表示模型的权重和偏置），其中θ是一个向量。我们的目标是最小化该损失函数，找到使损失函数最小化的最优参数θ*。

  1. 损失函数： J ( θ ) J(θ) J(θ)

  2. 学习率： α α α

  3. 衰减系数： β 1 和 β 2 β1和β2 β1和β2

  4. 一阶矩估计（m）和二阶矩估计（v）：
    Nadam算法为每个参数θ维护两个一阶矩估计和二阶矩估计，并使用它们来调整参数的学习率。

    在第t次迭代时，我们计算参数θ的梯度∇J(θ(t))，然后分别计算一阶矩估计m和二阶矩估计v：
    m ( t ) = β 1 ∗ m ( t − 1 ) + ( 1 − β 1 ) ∗ ∇ J ( θ ( t ) ) m(t) = β1 * m(t-1) + (1 - β1) * ∇J(θ(t)) m(t)=β1∗m(t−1)+(1−β1)∗∇J(θ(t))
    v ( t ) = β 2 ∗ v ( t − 1 ) + ( 1 − β 2 ) ∗ ( ∇ J ( θ ( t ) ) ) 2 v(t) = β2 * v(t-1) + (1 - β2) * (∇J(θ(t)))^2 v(t)=β2∗v(t−1)+(1−β2)∗(∇J(θ(t)))2

    其中：

    • ∇J(θ(t))是损失函数关于参数θ在第t次迭代的梯度（梯度向量）。
    • m(t)是一阶矩估计，它表示过去梯度的一阶矩（均值）。
    • v(t)是二阶矩估计，它表示过去梯度平方的二阶矩（平均平方）。
    • β1和β2是衰减系数，通常取值为0.9和0.999，分别用于控制一阶矩和二阶矩的衰减程度。

  5. 时间步数的衰减校正：
    Nadam算法引入了时间步数的衰减校正，用于修正动量的计算。

    β 1 t = β 1 ∗ ( 1 − 0.5 ∗ 0.9 6 ( t / 250 ) ) β1_t = β1 * (1 - 0.5 * 0.96^(t / 250)) β1t​=β1∗(1−0.5∗0.96(t/250))
    β 2 t = β 2 ∗ ( 1 − 0.9 9 t ) β2_t = β2 * (1 - 0.99^t) β2t​=β2∗(1−0.99t)

  6. 修正后的一阶矩估计（m_hat）和二阶矩估计（v_hat）：
    由于在算法初期估计偏向0，需要对一阶矩估计m和二阶矩估计v进行修正。

    m h a t ( t ) = m ( t ) / ( 1 − β 1 t ) m_hat(t) = m(t) / (1 - β1^t) mh​at(t)=m(t)/(1−β1t)
    v h a t ( t ) = v ( t ) / ( 1 − β 2 t ) v_hat(t) = v(t) / (1 - β2^t) vh​at(t)=v(t)/(1−β2t)

  7. 参数更新规则：
    使用修正后的一阶矩估计m_hat和二阶矩估计v_hat来更新参数θ。

θ ( t + 1 ) = θ ( t ) − ( α / ( s q r t ( v h a t ( t ) ) + ε ) ) ∗ ( β 1 t ∗ m h a t ( t ) + ( 1 − β 1 t ) ∗ ∇ J ( θ ( t ) ) ) θ(t+1) = θ(t) - (α / (sqrt(v_hat(t)) + ε)) * (β1_t * m_hat(t) + (1 - β1_t) * ∇J(θ(t))) θ(t+1)=θ(t)−(α/(sqrt(vh​at(t))+ε))∗(β1t​∗mh​at(t)+(1−β1t​)∗∇J(θ(t)))

其中：

  • α是学习率，用于控制参数更新的步长。
  • ε是一个小的常数，通常取较小的值（例如1e-8）以防止除以0。

Nadam算法通过引入Nesterov Accelerated Gradient（NAG）和Adam两种优化算法的特点，实现了对凸优化和非凸优化问题都有较好性能的优化算法。在深度学习中，Nadam广泛应用于训练复杂的深度神经网络和处理大规模数据集。

添加正则化

Nadam（Nesterov-accelerated Adaptive Moment Estimation）结合了Adam优化器的概念和Nesterov加速梯度的想法。在Nadam中添加正则化与在Adam中添加正则化非常相似，你只需要在计算梯度时包括正则化项。

以下是将L2正则化与Nadam结合使用的步骤：

  1. 计算损失函数的梯度（不包括正则化项）： ∇ J ( θ ( t ) ) \nabla J(\theta(t)) ∇J(θ(t))

  2. 计算正则化项的梯度： 2 λ θ ( t ) 2\lambda\theta(t) 2λθ(t)（对于L2正则化）

  3. 结合梯度： ∇ J ( θ ( t ) ) + 2 λ θ ( t ) \nabla J(\theta(t)) + 2\lambda\theta(t) ∇J(θ(t))+2λθ(t)

  4. 更新一阶矩估计：
    m ( t ) = β 1 m ( t − 1 ) + ( 1 − β 1 ) ( ∇ J ( θ ( t ) ) + 2 λ θ ( t ) ) m(t) = \beta_1 m(t-1) + (1-\beta_1)\left(\nabla J(\theta(t)) + 2\lambda\theta(t)\right) m(t)=β1​m(t−1)+(1−β1​)(∇J(θ(t))+2λθ(t))

  5. 更新二阶矩估计：
    v ( t ) = β 2 v ( t − 1 ) + ( 1 − β 2 ) ( ∇ J ( θ ( t ) ) + 2 λ θ ( t ) ) 2 v(t) = \beta_2 v(t-1) + (1-\beta_2)\left(\nabla J(\theta(t)) + 2\lambda\theta(t)\right)^2 v(t)=β2​v(t−1)+(1−β2​)(∇J(θ(t))+2λθ(t))2

  6. 修正一阶和二阶矩的偏差：
    m ^ ( t ) = m ( t ) 1 − β 1 t \hat{m}(t) = \frac{m(t)}{1-\beta_1^t} m^(t)=1−β1t​m(t)​
    v ^ ( t ) = v ( t ) 1 − β 2 t \hat{v}(t) = \frac{v(t)}{1-\beta_2^t} v^(t)=1−β2t​v(t)​

  7. 应用Nesterov修正：
    m Nesterov ( t ) = β 1 m ^ ( t ) + ( 1 − β 1 ) ( ∇ J ( θ ( t ) ) + 2 λ θ ( t ) ) m_{\text{Nesterov}}(t) = \beta_1 \hat{m}(t) + (1-\beta_1)\left(\nabla J(\theta(t)) + 2\lambda\theta(t)\right) mNesterov​(t)=β1​m^(t)+(1−β1​)(∇J(θ(t))+2λθ(t))

  8. 更新权重：
    θ ( t + 1 ) = θ ( t ) − α v ^ ( t ) + ϵ m Nesterov ( t ) \theta(t+1) = \theta(t) - \frac{\alpha}{\sqrt{\hat{v}(t)} + \epsilon} m_{\text{Nesterov}}(t) θ(t+1)=θ(t)−v^(t) ​+ϵα​mNesterov​(t)

代码实现与Adam类似，主要区别在于加入了Nesterov修正。你可以按照上述步骤编写代码来实现Nadam优化器，并包括你选择的正则化项。

注意：Nesterov修正为动量项增加了一种"预览"效果，以更准确地预测下一个参数更新的方向。与Adam相比，这可能会在某些情况下提供更好的训练性能。

代码演示
#include <iostream>
#include <vector>
#include <cmath>

// 定义损失函数（假设为均方误差）
double lossFunction(std::vector<double>& y_pred, std::vector<double>& y_actual) {
    double loss = 0.0;
    for (int i = 0; i < y_pred.size(); i++) {
        loss += 0.5 * std::pow(y_pred[i] - y_actual[i], 2);
    }
    return loss;
}

// 定义模型预测函数
std::vector<double> predict(std::vector<std::vector<double>>& data, std::vector<double>& weights) {
    std::vector<double> y_pred(data.size(), 0.0);
    for (int i = 0; i < data.size(); i++) {
        for (int j = 0; j < data[i].size(); j++) {
            y_pred[i] += data[i][j] * weights[j];
        }
    }
    return y_pred;
}

// Nadam优化函数
void nadamOptimization(std::vector<std::vector<double>>& data, std::vector<double>& labels,
                       std::vector<double>& weights, double learning_rate, double beta1, double beta2, double epsilon, int epochs) {
    int num_samples = data.size();
    int num_features = data[0].size();

    std::vector<double> m(num_features, 0.0); // 一阶矩估计
    std::vector<double> v(num_features, 0.0); // 二阶矩估计
    int t = 0; // 时间步数

    for (int epoch = 0; epoch < epochs; epoch++) {
        std::vector<double> y_pred = predict(data, weights);
        double loss = lossFunction(y_pred, labels);

        // 初始化梯度
        std::vector<double> gradient(num_features, 0.0);

        // 计算梯度
        for (int i = 0; i < num_samples; i++) {
            for (int j = 0; j < num_features; j++) {
                gradient[j] += (y_pred[i] - labels[i]) * data[i][j];
            }
        }

        // 更新时间步数
        t++;

        // 时间步数的衰减校正
        double beta1_t = beta1 * (1 - 0.5 * std::pow(0.96, t / 250));
        double beta2_t = beta2 * (1 - std::pow(0.99, t));

        // 更新一阶矩估计和二阶矩估计
        for (int j = 0; j < num_features; j++) {
            m[j] = beta1 * m[j] + (1 - beta1) * gradient[j];
            v[j] = beta2 * v[j] + (1 - beta2) * gradient[j] * gradient[j];
        }

        // 进行修正后的一阶矩估计和二阶矩估计
        std::vector<double> m_hat(num_features, 0.0);
        std::vector<double> v_hat(num_features, 0.0);
        for (int j = 0; j < num_features; j++) {
            m_hat[j] = m[j] / (1 - std::pow(beta1, t));
            v_hat[j] = v[j] / (1 - std::pow(beta2, t));
        }

        // 更新每个权重
        for (int j = 0; j < num_features; j++) {
            weights[j] -= (learning_rate / (std::sqrt(v_hat[j]) + epsilon)) * (beta1_t * m_hat[j] + (1 - beta1_t) * gradient[j]);
        }

        // 输出每次迭代的损失
        std::cout << "Epoch " << epoch + 1 << ", Loss: " << loss << std::endl;
    }
}

int main() {
    // 假设训练数据为2维特征
    std::vector<std::vector<double>> data = { {1.0, 2.0}, {2.0, 3.0}, {3.0, 4.0}, {4.0, 5.0}, {5.0, 6.0} };
    // 对应的标签
    std::vector<double> labels = {3.0, 4.0, 5.0, 6.0, 7.0};
    // 初始化权重
    std::vector<double> weights = {0.0, 0.0};

    double learning_rate = 0.1;
    double beta1 = 0.9;
    double beta2 = 0.999;
    double epsilon = 1e-8;
    int epochs = 1000;

    // 使用Nadam优化权重
    nadamOptimization(data, labels, weights, learning_rate, beta1, beta2, epsilon, epochs);

    // 打印最终学到的权重
    std::cout << "Weights: ";
    for (double w : weights) {
        std::cout << w << " ";
    }
    std::cout << std::endl;

    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
Nadam另一种算法：

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/羊村懒王/article/detail/144765
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号