devbox
羊村懒王
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

0-1背包问题&背包问题（动规/回溯/分支限界法&贪心）

作者：羊村懒王 | 2024-03-29 02:13:21

赞

踩

0-1背包问题

写在前面：仅为个人代码/总结，未必标准，仅供参考！如有错误，还望指出交流，共同进步！

（一）0-1背包问题

在这里插入图片描述

【动态规划法】

一、算法思路

0-1背包问题具有最优子结构性质和重叠子问题性质。
首先定义m(i,j)：从物品i、i+1、…、n-1、n中选择物品装入容量大小为j的背包，使该背包的总价值最大，最大值为m(i,j)，即最优值。
假设背包容量为c，物品总数n，物品i的重量表示wi，价值表示vi，于是0-1背包问题的最优值为m(1,c)。计算m(1,c)的值之前，先递归地定义最优值的计算方法：
（1）当背包剩余容量为j时，且j≥wi, m(i,j)= max{ m(i+1,j), m(i+1,j-wi)+vi)}。即当此时的背包剩余容量大于物品i的重量，于是在选取物品i和不选取物品i之中选择较大者。
（2）当背包剩余容量为j时，且0<j< wi, m(i,j)= m(i+1,j);。说明物品i的重量大于背包此时剩余容量，装不下，舍弃。
（3）最小的子问题，当背包剩余容量为j、且只有一个物品n供选择时，此时，若j≥wn, 则最大价值为vn，即 m(n,j)=vn；若j < wn, 则最大价值为0,即 m(n,j) = 0。

二、递归式

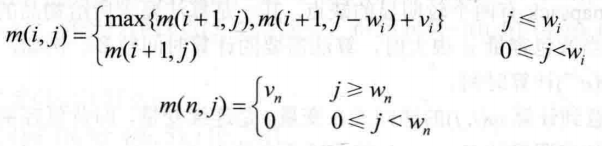
在这里插入图片描述

三、实现代码

#include <bits/stdc++.h>
using namespace std;
void getData(int* a,int* b,int n)
{
    srand(time(0));
    for(int i=1;i<=n;i++)
    {
        a[i]=rand()%15+1;
    }
    for(int i=1;i<=n;i++)
    {
        b[i]=rand()%15+1;
    }
}
void Knapsack(int* v,int* w, int c, int n,int (*m)[21])
{
    int jMax=min(w[n]-1,c);//首先处理第n个物品
    for(int j=0;j<=jMax;j++)//剩余容量＜物品n重量
    {
        m[n][j] = 0;
    }
    for(int j=w[n];j<=c;j++)//剩余容量≥物品n重量
    {
        m[n][j] = v[n];
    }
    for(int i=n-1;i>1;i--)
    {
        jMax=min(w[i]-1,c);
        for(int j=0;j<=jMax;j++)//当背包剩余容量为j时，且0<j<wi
            m[i][j] = m[i+1][j];
        for(int j=w[i];j<=c;j++)//当背包剩余容量为j时，且j≥wi
            m[i][j]=max(m[i+1][j],m[i+1][j-w[i]]+v[i]);
    }
    //处理第1个物品
    m[1][c]=m[2][c];
    if(c>=w[1])
        m[1][c]=max(m[1][c],m[2][c-w[1]]+v[1]);
}
void Traceback(int (*m)[21], int* w, int c, int n,int* x)
{
    for(int i=1;i<n;i++)
    {
        if(m[i][c]==m[i+1][c])
            x[i]=0;
        else
        {
            x[i]=1;
            c-=w[i];
        }
    }
    x[n]=(m[n][c])?1:0;
}
int main()
{
    cout<<"（每次随机生成的测试数据物品个数默认为10，背包容量默认为20，物品重量、价值为1-15的随机数）"<<endl;
    int w[11]={0};
    int v[11]={0};
    int x[11];
    getData(w,v,10);
    cout<<"物品重量为：";
    for(int i=1;i<=10;i++)
    {
        cout<<w[i]<<' ';
    }
    cout<<endl<<"物品价值为：";
    for(int i=1;i<=10;i++)
    {
        cout<<v[i]<<' ';
    }
    cout<<endl;
    int m[11][21];
    Knapsack(v,w,20,10,m);
    cout<<"装入背包物品最大总价值："<<m[1][20]<<endl;
    Traceback(m,w,20,10,x);
    cout<<"解向量为：";
    for(int i=1;i<=10;i++)
    {
        cout<<x[i]<<' ';
    }
    cout<<endl;
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82

四、算法效率

算法Knapsack需要O(nc)计算时间，算法Trackback需要O(n)计算时间。

【回溯法】

一、算法思想

首先明确0-1背包问题的解空间为子集树。对于每一个物品i，只有选与不选2个决策，总共有n个物品，可以顺序依次考虑每个物品，这样就形成了一棵二叉解空间树。
搜索状态空间树时，只要左子节点是可一个可行结点，搜索就进入其左子树。对于右子树时，先计算限界函数，以判断是否将其减去（剪枝），即当右子树中有可能包含最优解时才进入右子树，否则剪去右子树。
当限界函数Bound():当前价值cv+剩余容量可容纳的最大价值r<=当前最优价值bestv时，可剪去右子树。
为了更好地计算和运用上界函数剪枝，选择先将物品按照其单位重量价值从大到小排序，此后就按照该顺序考虑各个物品。

二、实现代码

#include <bits/stdc++.h>
using namespace std;
class Knap{
    friend int Knapsack(int*,int*,int,int,int[]);
private:
    int Bound(int i);
    void Backtrack(int i);
    int c;
    int n;
    int *x;
    int *bestx;
    int *w;
    int *p;
    int cw;
    int cp;
    int bestp;
};
class Object
{
    friend int Knapsack(int*,int*,int,int,int*);
public:
    int ID;
    float d;
};
bool cmp(Object A,Object B)
{
    return A.d>B.d;
}
int Knap::Bound(int i)
{
    int cleft=c-cw;
    int b=cp;
    while(i<=n&&w[i]<=cleft)
    {
        cleft-=w[i];
        b+=p[i];
        i++;
    }
    if(i<=n)
    {
        b+=p[i]*cleft/w[i];
    }
    return b;
}
void Knap::Backtrack(int i)
{
    if(i>n)//到达叶结点
    {
        for(int j=1;j<=n;j++)
        {
            bestx[j]=x[j];
        }
        bestp=cp;
        return;
    }
    if(cw+w[i]<=c)//进入左子树
    {
        x[i]=1;
        cw+=w[i];
        cp+=p[i];
        Backtrack(i+1);
        cw-=w[i];
        cp-=p[i];
        x[i]=0;
    }
    if(Bound(i+1)>bestp)//进入右子树
        Backtrack(i+1);
}
int Knapsack(int* p,int * w,int c,int n,int* bestx)
{
    int W=0;
    int P=0;
    Object *Q=new Object[n];
    for(int i=1;i<=n;i++)
    {
        Q[i-1].ID=i;
        Q[i-1].d=10*p[i]/w[i];
        P+=p[i];
        W+=w[i];
    }
    if(W<=c)
        return P;
    sort(Q+1,Q+n+1,cmp);
    Knap K;
    K.p=new int[n+1];
    K.w=new int[n+1];
    K.x=new int[n+1];
    for(int i=1;i<=n;i++)
    {
        K.p[i]=p[Q[i-1].ID];
        K.w[i]=w[Q[i-1].ID];
        K.x[i]=0;
    }
    K.cp=0;
    K.cw=0;
    K.c=c;
    K.n=n;
    K.bestp=0;
    K.bestx=bestx;
    K.Backtrack(1);
    for(int i=1;i<=n;i++)
    {
        K.x[i]=K.bestx[i];
    }
    for(int i=1;i<=n;i++)
    {
        K.bestx[Q[i-1].ID]=K.x[i];
    }
    delete []Q;
    delete []K.w;
    delete []K.p;
    delete []K.x;
    return K.bestp;
}
int main()
{
    int n,c;
    cin>>n>>c;
    int *p,*w,*bestx;
    p=new int[n+1];
    w=new int[n+1];
    bestx=new int[n+1];
    for(int i=1;i<=n;i++)
    {
        cin>>w[i];
    }
    for(int i=1;i<=n;i++)
    {
        cin>>p[i];
        bestx[i]=0;
    }
    int res=Knapsack(p,w,c,n,bestx);
    cout<<res<<endl;
    for(int i=1;i<=n;i++)
    {
        cout<<bestx[i]<<' ';
    }
    cout<<endl;
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140

三、算法效率

计算上界需要O(n)时间，最坏情况下有O(n2)个右儿子结点需要计算上界，而在遍历到叶结点时需要一次性更新最优解，计算时间为O(n)，故回溯算法Backtrack所需的计算时间为O(n22n)。

四、更新最优解算法改进

class Knap{
    friend int Knapsack(int*,int*,int,int,int[]);
private:
    int Bound(int i);
    void Backtrack(int i);
    int c;
    int n;
    int *x;
    int *bestx;
    int *w;
    int *p;
    int cw;
    int cp;
    int bestp;
    int ii;//增加最优解回溯标志
};
//每当算法回溯一层，将x[i]存入bestx[i]，在每个结点处更新bestx只需要O(1)时间
void Knap::Backtrack(int i)
{
    if(i>n)//到达叶结点
    {
        ii=n;
        bestp=cp;
        return;
    }
    if(cw+w[i]<=c)//进入左子树
    {
        x[i]=1;
        cw+=w[i];
        cp+=p[i];
        Backtrack(i+1);
        if(ii==i) {bestx[i]=1;ii--;}
        cw-=w[i];
        cp-=p[i];
        x[i]=0;
    }
    if(Bound(i+1)>bestp)//进入右子树
    {
        Backtrack(i+1);
        if(ii==i) {bestx[i]=0;ii--;}
    }
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42

【优先队列式分支限界法】

一、算法思想

分支限界法常以广度优先或最小耗费优先（最大效益优先）方式搜索问题的解空间树， 0-1背包问题的解空间树是一个颗子集树。
对于0-1背包问题中的每个活结点只有两个儿子结点，分别表示选取和不选取物品i；在判断儿子结点是否能加入到活结点表中，有两个函数条件需要满足，一个是约束函数，判断能否满足背包容量约束，另一个是限界函数，判断是否可能有最优解。
为了尽快找到0-1背包问题的解，每次选取下一个活结点成为扩展结点的判断依据是当前情况下最有可能找到最优解的下一个结点。因此，每次选择扩展结点的方法：当前情况下，在活结点表中选择活结点的上界uprofit（通过限界函数Bound求出）最大的活结点成为当前的扩展结点，即以uprofit为优先级将活结点插入到优先队列中，每一次选取优先级最高的结点作为当前拓展结点。 这一过程一直持续到找到所需的解或活结点表为空时为止。
为了在活结点表中选择拥有最大的上界uprofit的活结点，在活结点表上实现优先队列。

二、算法步骤

首先，根据每个物品的重量和价值计算出物品的单价，根据单价将物品进行排序，以下是优先队列式分支限界法的搜索过程：
①搜索解空间建立二叉树，从根结点开始。
②广度优先搜索二叉树，并用upfrofit表示活结点的优先级构建最大堆。
③选取优先级最高的活结点作为扩展结点，找出可行解。
④检查左儿子结点是否是可行结点（即上界大于当前最优值且加上该物品的重量不超过背包容量），如果是则将它加入到活结点优先队列中，而当前扩展结点的右儿子一定是可行结点，仅当右儿子满足上界约束时才将它加入到活结点优先队列中。
⑤维护堆结构，使得堆顶元素依然是优先级最高的结点。（构建优先队列可直接调用C++STL库中的priority_queue，插入活结点自动维护）
⑥重复③④⑤步骤直到优先队列为空。

三、实现代码

#include <bits/stdc++.h>
using namespace std;
typedef int Typew;
typedef int Typep;
//物品类
class Object{
	friend Typep Knapsack(Typew *, Typep *, Typew, int, int *);
public:
	int operator <= (Object a) const{
		return (d >= a.d);
	}
private:
	int ID; //物品编号
	float d; //单位重量价值
};
//树结点类
class bbnode{
	friend class Knap;
	friend Typep Knapsack(Typew *, Typep *, Typew, int, int *);
private:
	bbnode *parent; //指向父节点的指针
	int LChild; //左儿子结点标记
};
//堆结点类
class HeapNode{
	friend class Knap;
	friend class MaxHeap;
public:
	operator Typep()const{return uprofit;};
private:
	Typep uprofit, //结点的价值上界
		  profit; //结点所相应的价值
	Typew weight; //结点所相应的重量
	int level; //活结点在子集树中所处的层序号
	bbnode *elemPtr; //指向该活结点在子集树中相应结点的指针
};
//0-1背包问题的主类
class Knap{
	friend Typep Knapsack(Typew *, Typep *, Typew, int, int *);
public:
	Typep MaxKnapsack();
private:
	priority_queue<HeapNode> H;
	//限界函数：计算结点价值上界
	Typep Bound(int i);
	//将活结点插入子集树和优先队列中
	void AddLiveNode(Typep up, Typep cp, Typew cw, int ch, int level);
	bbnode *E; //指向扩展结点的指针
	Typew c; //背包容量
	int n; //物品总数
	Typew *w; //物品重量数组
	Typep *p; //物品价值数组
	Typew cw; //当前装包重量
	Typep cp; //当前装包价值
	int *bestx; //最优解
};

Typep Knap::MaxKnapsack()
{
	bestx = new int [n+1];
	int i = 1; //生成子集树中的第一层的结点
	E = 0; 
	cw = 0;
	cp = 0;
	Typep bestp = 0; //当前最优值
	Typep up = Bound(1); // 选取物品1之后的价值上界
	//当选择左儿子结点时，考虑约束函数
	//当选择右儿子结点时，考虑限界函数
	while (i != n+1)
	{
		//检查当前扩展结点的左儿子结点
		Typew wt = cw + w[i]; //当前选择物品i之后的总重量wt
		if(wt <= c) //左儿子结点可行
		{
			if(cp + p[i] > bestp)
				bestp = cp + p[i];
			AddLiveNode(up, cp + p[i], cw + w[i], 1, i);
		}
		//检查当前扩展结点的右儿子结点
		up = Bound(i + 1); //未选择物品i之后的价值上界
		if(up >= bestp)
			AddLiveNode(up, cp, cw, 0, i);
		//从优先队列中选择uprofit最大的结点成为扩展结点
		HeapNode N;
		N=H.top();
		H.pop();
		E = N.elemPtr;
		cw = N.weight;
		cp = N.profit;
		up = N.uprofit;
		i = N.level + 1; 
	}
	//从子集树中的某叶子结点开始构造当前最优解
	for (int i = n; i > 0; i--)
	{
		bestx[i] = E->LChild;
		E = E->parent;
	}
	return cp;
}
Typep Knap::Bound(int i)
{
	Typew cleft = c - cw;
	Typep b = cp;
	while (i<=n && w[i] <= cleft)
	{
		cleft -= w[i];
		b += p[i];
		i++;
	}
	if(i<=n) b += p[i]/w[i] * cleft;
	return b;
}
void Knap::AddLiveNode(Typep up, Typep cp, Typew cw, int ch, int level)
{
	bbnode *b=new bbnode;
    b->parent=E;
    b->LChild=ch;
	HeapNode N;
    N.uprofit=up;
    N.profit=cp;
    N.weight=cw;
    N.level=level;
	N.elemPtr=b;
	H.push(N);
}
Typep Knapsack(Typew *w, Typep *p, Typew c, int n, int *bestx)
{
	Typew W = 0;
	Typep P = 0;
	Object *Q = new Object[n];
	for(int i =1; i<=n; i++)
	{
		Q[i-1].ID = i;
		Q[i-1].d = 1.0*p[i]/w[i];
		P += p[i];
		W += w[i];
	}
	if (W <= c)
	{
		for(int i =1; i<=n; i++)
		{
			bestx[i] = p[i];
		}
		return P;
	}
	//采用简单冒泡排序，对物品以单位重量价值降序排序
	for(int i = 1; i<n; i++)
		for(int j = 1; j<= n-i; j++)
		{
			if(Q[j-1].d < Q[j].d)
			{
				Object temp = Q[j-1];
				Q[j-1] = Q[j];
				Q[j] = temp;
			}
		}
	Knap K;
	K.p = new Typep [n+1];
	K.w = new Typew [n+1];
	for(int i = 1; i<=n; i++)
	{
		K.p[i] = p[Q[i-1].ID];//以单位重量价值降序排序
		K.w[i] = w[Q[i-1].ID];//以单位重量价值降序排序
	}
	K.cp = 0;
	K.cw = 0;
	K.c = c;
	K.n = n;
	Typep bestp = K.MaxKnapsack();
	for(int i = 1; i<=n; i++)
	{
		bestx[Q[i-1].ID] = K.bestx[i];
	}
	delete [] Q;
	delete [] K.w;
	delete [] K.p;
	delete [] K.bestx;
	return bestp;
}
Typep p[10001];
Typew w[10001];
int bestx[10001];
int main()
{
        int N;
        Typew c; //背包容量
        int bestp; //最优值
        cin>>N>>c;
        for(int i=1;i<=N;i++)
        {
            cin>>w[i]>>p[i];
        }
        bestp = Knapsack(w, p, c, N, bestx);
        for(int i = 1; i <= N; i++)
        {
            if(i ==1 ) cout<<"解向量：";
            cout<<bestx[i];
            if(i != N) cout<<",";
            else
                cout<<endl;
        }
        cout<<"背包最优价值："<<bestp<<endl;
    }
	return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72
  • 73
  • 74
  • 75
  • 76
  • 77
  • 78
  • 79
  • 80
  • 81
  • 82
  • 83
  • 84
  • 85
  • 86
  • 87
  • 88
  • 89
  • 90
  • 91
  • 92
  • 93
  • 94
  • 95
  • 96
  • 97
  • 98
  • 99
  • 100
  • 101
  • 102
  • 103
  • 104
  • 105
  • 106
  • 107
  • 108
  • 109
  • 110
  • 111
  • 112
  • 113
  • 114
  • 115
  • 116
  • 117
  • 118
  • 119
  • 120
  • 121
  • 122
  • 123
  • 124
  • 125
  • 126
  • 127
  • 128
  • 129
  • 130
  • 131
  • 132
  • 133
  • 134
  • 135
  • 136
  • 137
  • 138
  • 139
  • 140
  • 141
  • 142
  • 143
  • 144
  • 145
  • 146
  • 147
  • 148
  • 149
  • 150
  • 151
  • 152
  • 153
  • 154
  • 155
  • 156
  • 157
  • 158
  • 159
  • 160
  • 161
  • 162
  • 163
  • 164
  • 165
  • 166
  • 167
  • 168
  • 169
  • 170
  • 171
  • 172
  • 173
  • 174
  • 175
  • 176
  • 177
  • 178
  • 179
  • 180
  • 181
  • 182
  • 183
  • 184
  • 185
  • 186
  • 187
  • 188
  • 189
  • 190
  • 191
  • 192
  • 193
  • 194
  • 195
  • 196
  • 197
  • 198
  • 199
  • 200
  • 201
  • 202
  • 203
  • 204
  • 205
  • 206

（二）背包问题

与0-1背包问题类似，所不同的是在选择物品i装入背包时，可以选择物品i的一部分而不一定要全部装入背包（1≤i≤n），使得背包价值最大。

【贪心算法】

一、算法思路

为了尽可能的得到最优解,选择物品时,总是选择v[i]/w[i]最大的物品装进去。所以在程序的开始，首先定义物品结构体，结构体包含物品的序号、重量、价值、是否放进背包的信息，然后对物品按照v[i]/w[i]即单位重量价值从大到小进行排序,再调用Knapsack函数根据性价比将物品放进背包，最后放不下某个物品时将该物品的一部分装进背包直至背包被装满，完成后对物品按序号从小到大排序，调用Traceback函数输出相应序号的物品是否被放进背包、放进了多少。

二、实现代码

#include<bits/stdc++.h>
using namespace std;
struct object
{
    int num;
    float value;
    float weight;
    float flag;
};
bool cmp1(object A,object B)
{
    float u=B.weight,v=A.weight;
    return (A.value*u)>(B.value*v);
}
bool cmp2(object A,object B)
{
    return A.num<B.num;
}
float Knapsack(object* O,float c,int n)
{
    float curweight=0,curvalue=0;
    for(int i=0;i<n;i++)
    {
        if((O[i].weight+curweight)<=c)
        {
            curvalue+=O[i].value;
            curweight+=O[i].weight;
            O[i].flag=1.0;
        }
        else if(c-curweight>0)
        {
            O[i].flag=(c-curweight)/O[i].weight;
            curvalue+=O[i].flag*O[i].value;
            curweight=c;
        }
        else
        {
            O[i].flag=0;
        }
    }
    return curvalue;
}
void Traceback(object* O,int n)
{
    for(int i=0;i<n;i++)
    {
        cout<<O[i].flag<<' ';
    }
    cout<<endl;
}
int main()
{
    cout<<"请输入物品数量:";
    int n;
    cin>>n;
    object O[n];
    for(int i=0;i<n;i++)
    {
        cout<<"请输入第"<<i+1<<"个物品的重量和价值:";
        cin>>O[i].weight>>O[i].value;
        O[i].num=i+1;
    }
    cout<<"请输入背包的容量:";
    float c;
    cin>>c;
    sort(O,O+n,cmp1);
    float res=Knapsack(O,c,n);
    cout<<res<<endl;
    sort(O,O+n,cmp2);
    Traceback(O,n);
    return 0;
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27
  • 28
  • 29
  • 30
  • 31
  • 32
  • 33
  • 34
  • 35
  • 36
  • 37
  • 38
  • 39
  • 40
  • 41
  • 42
  • 43
  • 44
  • 45
  • 46
  • 47
  • 48
  • 49
  • 50
  • 51
  • 52
  • 53
  • 54
  • 55
  • 56
  • 57
  • 58
  • 59
  • 60
  • 61
  • 62
  • 63
  • 64
  • 65
  • 66
  • 67
  • 68
  • 69
  • 70
  • 71
  • 72

（三）0-1背包问题的拓展——考虑容积

在这里插入图片描述

【动态规划法】

一、算法思路

该问题是原0-1背包问题的拓展，增加了容积这一限制条件，因此将原来的二维数组m(i,j)增加一维变为m(i,j,k)，定义m(i,j,k)为从物品0、1、…、i-1、i中选择物品装入容量大小为j、容积为k的背包，使该背包的总价值最大，最大值为m(i,j,k)，算法思路和原0-1背包问题的动态规划法思路一致。

二、递归式

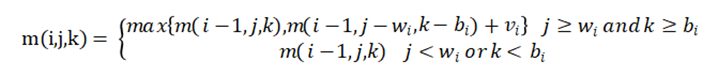
在这里插入图片描述

三、实现代码

int m[n][c+1][d+1]={0};
void Knapsack(int* v,int* w,int* b,int c,int d,int n)
{
	for(int j=0;i<=c;j++)
	{
		for(int k=0;k<=d;k++)
		{
			if(w[0]<=j&&b[0]<=k)
				m[0][j][k]=v[0];
			else
				m[0][j][k]=0;
		}
	}
	for(int i=1;i<n;i++)
	{
		for(int j=1;j<=c;j++)
		{
			for(int k=1;k<=d;k++)
			{
				if(w[i]<=j&&b[i]<=k)
					m[i][j][k]=max(m[i-1][j][k],m[i-1][j-w[i]][k-b[i]]+v[i]);
				else
					m[i][j][k]=m[i-1][j][k];
			}
		}
	}
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
  • 14
  • 15
  • 16
  • 17
  • 18
  • 19
  • 20
  • 21
  • 22
  • 23
  • 24
  • 25
  • 26
  • 27

（四）完全背包问题、多重背包问题

一、完全背包问题：每一种物品有无限个，因此不需要考虑每件物品是否已经被取。

int m[c+1]={0};
for(int i=1;i<=n;i++) 
{
    for(int j=w[i];j<=c;j++) 
    {
        m[j] = max(m[j], m[j - w[i]] + v[i]);
    }
}

  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8

二、多重背包问题：限定每一种物品的个数，解决多重背包问题可将其转化为0-1背包问题求解。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/羊村懒王/article/detail/333099
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号