矩阵的对数运算公式_考研竞赛数学|公式

考研竞赛数学|公式

高等数学（篇一）

（一）基础公式

「初等函数」

• 对数函数

对数运算法则

对数恒等式

换底公式

• 三角函数

加法公式

倍角公式

半角公式

和差化积公式：

❝ 记忆口诀：正加正，正在前.余加余，余并肩.正减正，余在前.余减余，负正弦.前角用和后角差，二倍二分作乘法.
❞

积化和差公式：

❝ 记忆口诀：正余二分正弦和，余正二分正弦差，余余二分余弦和，正正负半余弦差，前角用和后角差.
❞

诱导公式

❝ 记忆口诀：奇变偶不变，符号看象限.（或者分变整不变，符合看象限.）
❞

正弦定理：

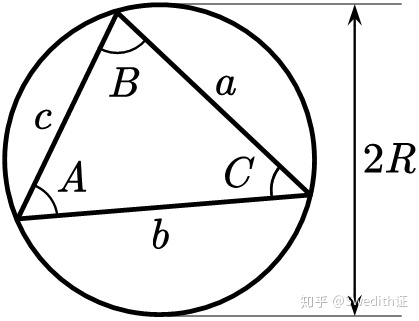
余弦定理：

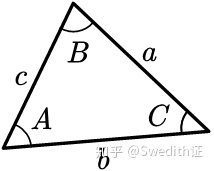
辅助角公式

❝ 记忆：很多人在利用辅助角公式时，经常忘记反正切到底是

还是

，导致做题出错。其实有一个很方便的记忆技巧，就是不管用正弦还是余弦来表示

，分母的位置永远是你用来表示函数名称的系数。 例如用正弦来表示

，则反正切就是

（即正弦的系数

在分母）。如果用余弦来表示,那反正切就要变成

（余弦的系数

在分母）。——百度

❞

三角恒等式

「代数」

不等式

更一般的还有如下关系：

乘法与因式分解

部分分式

经过有理式的恒等变形，任何有理式总能化为某个既约分式。如果既约分式是只含有一个自变数的真分式，还可进一步化为若干个既约真分式之和。这几个分式便称为原来那个既约分式的部分分式。

式中

式中

式中

式中

多项式定理

二项式定理

多项式定理

排列与组合

组合公式：

比例公式

等比定理：

阶乘

阶乘定义类公式

斯特林公式

阶乘有限和公式

特殊数列前n项的和