【数据分析】初识 AB 测试_同一个群体可以近乎同时进行多个ab测试吗

1.简述 AB 测试

AB 测试是指为了评估模型 / 项目的效果，在 APP / PC 端同时设计多个版本，在同一时间维度下，分别让组成成分相同（相似）的访客群组随机访问这些版本，收集各群组的用户体验数据和业务数据，最后分析评估出最好的版本正式采用。

AB 测试的整个过程分为三个部分：试验分组、进行试验、分析结果。其中分组是最重要的一个环节，如果分组不合理，之后的实验都是徒劳的。

2.介绍常用的 AB 测试的分组方法

• 基于设备号、用户唯一标识（如用户 ID 等）的尾号或者其他指标进行分组，如按照尾号为奇数或者偶数分为两组，在分组过程中不需要对这些唯一标识进行处理。

• 基于唯一标识，通过一个固定的哈希函数对用户唯一标识进行哈希取模、分桶。将用户均匀的分配至若干个实验桶中，可以将桶简单的理解为小组。相比于直接基于唯一标识进行分组，这种方法能够进一步将用户打散，提高分组的效果。

3.面对多个实验并行的情况，如何保证分组的合理性？

在实际工作中，通常会出现多个实验并行的情况，并且由于网站或者 APP 的流量是有限的，同一批用户可能会同时作为多个实验的数据源，此时进行分组就要全方位地考虑目前正在进行的实验情况。

这里需要引入 域 的概念。对于所有的用户，需要在所有实验开始前将其划分为不同的域，不同域之间的用户相互独立，交集为空。对于一些比较重要的实验，可以专门为其划分出一部分用户，在该实验进行期间，不会针对这些用户进行其他实验。这称为 独占域。在进行实验时，只需要基于这些用户的哈希值分组即可。

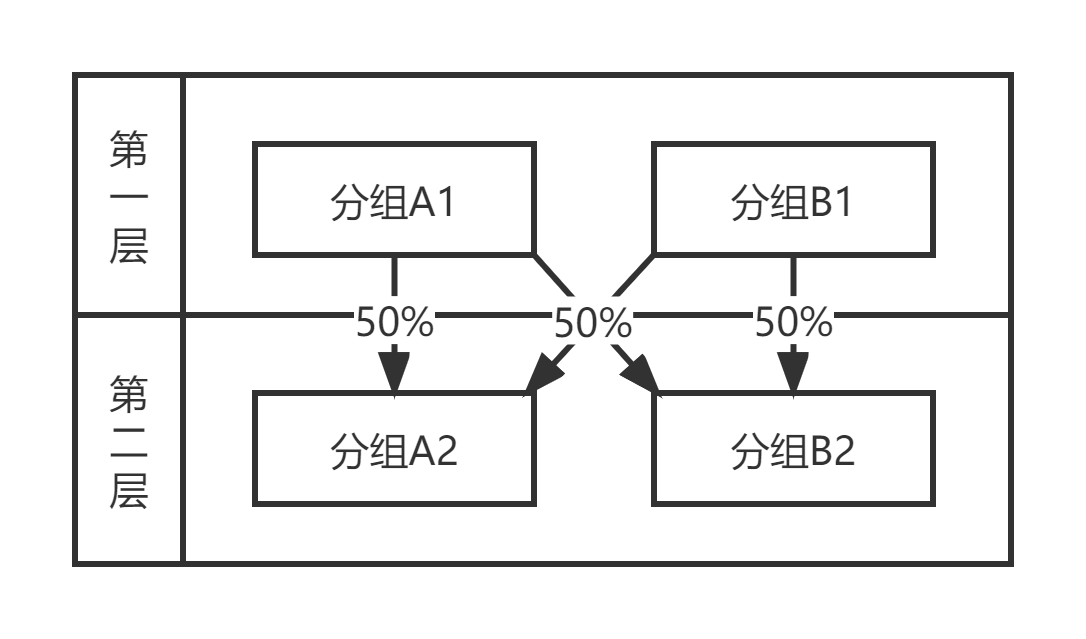
与独占域对应的是 共享域，即针对域中的用户同时进行多组 AB 测试。此时在分组的时候就要考虑分层。为了方便理解，这里将每一个实验作为单独的一层，根据实验开始的时间，将实验按照从上层到下层的顺序进行排列，下一层实验进行分组时，需要将上一层实验各个分组打散。

需要注意的是，在同一个共享域不可以同时进行过多的实验，即使基于正交的方法可以保证随机性，但通常最多也不要超过 7 个实验同时进行，同时也要思考是否有办法验证分组的随机性。

4.如何充分证明 AB 测试分组的随机性？

理论上，通过基于正交的方法，可以保证用户分组的随机性，但是为了防止意外情况发生，还需要引入 AA 测试 的概念，进一步保证分组的随机性。

假设 A 版本表示老版本，B 版本表示新版本。按照 6:4 的比例进行划分，同时从 A 版本中划分 20% 的用户进行 AA 测试。最终验证结果时，首先要保证 AA 测试通过，确保分组的合理性。然后再看 AB 测试是否通过。

当然对于在进行 AB 测试之前，是否要进行 AA 测试，仍然是一个具有争议的问题。

5.简述 AB 测试背后的理论支撑

根据中心极限定理，当数据量足够大时，可以认为样本均值近似服从正态分布。然后结合假设检验的内容，推翻或接受原假设。

6.如何通过 AB 测试证明新版本用户的转化率高于老版本用户的转化率？

• 将新版本用户是否下单的样本记为 $x_1,x_2,...,x_n$，将老版本用户是否下单的样本记为 $y_1,y_2,...,y_n$，最终下单记为 1，否则记为 0。

• 随着样本量的增加，$\overline{X}$ 趋近于 $N({\mu }_x,\frac{{\sigma }_x^2}{n})$、$\overline{Y}$ 趋近于 $N({\mu }_y,\frac{{\sigma }_y^2}{n})$。其中 $\mu$、$\sigma$ 参数可以用无偏统计量 $\overline{x}=\frac{{\sum }_{i=1}^n{x}_i}{n}$，$s^2=\frac{{\sum }_{i=1}^n(x_i-\overline{x}{)}^2}{n-1}$ 代替，于是有 $\overline{X}\sim N(\overline{x},\frac{s_x^2}{n})$，$\overline{Y}\sim N(\overline{y},\frac{s_y^2}{n})$。而在分组中已经保证了 $\overline{X}$ 、$\overline{Y}$ 相互的独立性，因此 $\overline{X}-\overline{Y}\sim N(\overline{x}-\overline{y},\frac{{\sigma }_x^2}{n}+\frac{{\sigma }_y^2}{n})$

• $\overline{X}$ 、$\overline{Y}$ 分别代表新老版本用户的转化率，现在要证明新版本用户的转化率高于老版本用户的转化率。
  原假设 $H_0$：新版本用户的转化率低于或等于老版本用户的转化率。
  备择假设 $H_1$：新版本用户的转化率高于老版本用户的转化率。
  通过拒绝 $H_0$、接受 $H_1$，证明新版本用户的转化率高于老版本用户的转化率。

参考：《数据分析师求职面试指南》，徐麟