羊村懒王

这个屌丝很懒，什么也没留下！

热门标签

NLP： LDA主题模型

作者：羊村懒王 | 2024-04-04 20:47:25

踩

lda主题模型

Essence本质：LDA模型主要包括主题分布θ和词语分布 $\Phi$ ，

主题分布：各个主题在文档中出现的概率分布。
词语分布：各个词语在某个主题下出现的概率分布。

pLSA模型中这两个分布是固定的，由期望最大化EM(Expectation Maximization)算法求参；

而LDA模型中这两个分布是随机的，由Dirichlet分布生成，而Dirichlet分布的参数α和β由Gibbs采样生成。

1. 简介

1.1 LDA overall framework

2.3 二项分布Binomial Distribution

2.4 多项分布Multinomial Distribution

2.5 Beta分布，二项分布的共轭先验分布

2.6 Dirichlet分布，多项分布的共轭先验分布

3.2.1 Unigram model一元模型

3.2.2 Mixture of unigrams model

3.3 pLSA模型(Probabilistic latent semantic analysis)

3.3.1 steps: pLSA得到"文档-词项"生成模型的步骤

3.3.2 example: pLSA模型生成文档

3.3.3 Problem: 词袋模型，未关注词与词之间的顺序

3.3.4 Understanding: pLSA模型

4.1 LDA implementation 1

4.2 LDA implementation 2

4.3 Ida2vec implementation

1. 简介

1.1 LDA overall framework

(1) 一个函数：gamma函数

(2) 四个分布：二项分布、多项分布、beta分布、Dirichlet分布

(3) 一个概念和一个理念：共轭先验、贝叶斯框架

(4) 两个模型：pLSA和LDA

(5) 一个采样：Gibbs采样

1.2 Concept

LDA(Latent Dirichlet Allocation)主题模型，它可以将文档集中每篇文档的主题以概率分布的形式给出。

1.3 对比：词袋模型和LDA模型

词袋模型：推测一篇文章是如何生成的

以一定的概率选取某个主题，再以一定的概率选取那个主题下的某个单词，不断重复这两步，最终生成一篇文档。(其中不同颜色的词语分别对应上图中不同主题)

LDA模型：根据给定的training文档，反推其主题分布。

各篇文章分别都写了些啥主题，且各篇文章中各个主题出现的概率大小(主题分布)是啥

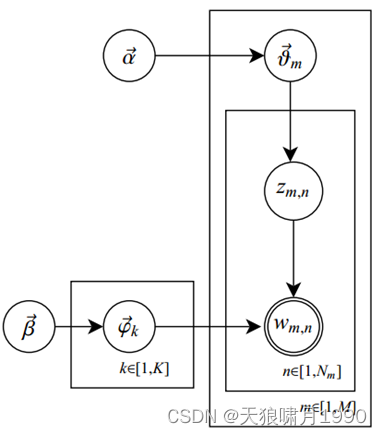
1.4 LDA模型生成文档过程

在LDA topic model中，文档生成方式如下：

1) 从Dirichlet分布α中取样生成文档i的主题分布θi；

2) 从主题多项分布θi中取样生成文档第j个词的主题Zi,j

3) 根据主题Zi,j，从Dirichlet分布β中取样生成主题Zi,j对应的词语分布 $\Phi z_{i,j}$

4) 从词语多项分布 $\Phi z_{i,j}$ 中采样最终生成词语Wi,j

其中，Beta分布是二项分布的共轭先验概率分布，而Dirichlet分布是多项式分布的共轭先验概率分布。

2. LDA基础知识

2.1 Gamma函数

$\Gamma (x) = \int_{0}^{\infty } t^{x-1}e^{-t}dt$

2.2 伯努利分布

伯努利分布就是最简单的0-1分布，搞科学的这群人就喜欢炒概念！！！

p(x=0)=p; p(x=1)=1-p

2.3 二项分布Binomial Distribution

$C_{n}^{k}p^{k}(1-p)^{n-k}$

2.4 多项分布Multinomial Distribution

二维分布扩展到多维的情况

$p(x_{1}, x_{2}, ...,x_{k}; n, p_{1}, p_{2}, ...,p_{k}) = \frac{n!}{x_{1}!x_{2}!...x_{k}!} p_{1}^{x_{1}}p_{2}^{x_{2}}...p_{k}^{x_{k}}$

2.5 Beta分布，二项分布的共轭先验分布

给定参数α>0和β>0，取值范围为[0,1]的随机变量x的概率密度函数：

$f(x; \alpha ,\beta ) = \frac{1}{B(\alpha, \beta)} x^{\alpha-1} (1-x)^{\beta-1}$

其中， $\frac{1}{B(\alpha, \beta)} = \frac{\Gamma(\alpha + \beta)}{\Gamma(\alpha)\Gamma(\beta)}$ , $\Gamma(x)$ 是gamma函数

2.6 Dirichlet分布，多项分布的共轭先验分布

Dirichlet分布是Beta分布在高维上的推广

$f(x_{1},x_{2},...,x_{k}; \alpha_{1}, \alpha_{2},..., \alpha_{k}) = \frac{1}{B(x)}\prod _{i=1}^{k}x_{i}^{\alpha _{i}-1}$

2.7 先验分布与后验分布

先验分布：即根据已有数组的概率分布，推测未发生事件的概率。e.g. 已有天气数据，推测明天是否下雨。
后验分布：即根据预测事件发生概率，分析已有数据的概率分布。e.g. 已经天气预报数据因为涂鸦丢失而损坏了一部分，只能得到部分概率分布，这时根据明天下雨事件的概率，推测已有天气数据的概率分布。

3. LDA主题模型

3.1 频率派与贝叶斯派

频率派：把需要推断的参数θ看作是固定的未知数。即概率θ是未知的，但最起码是确定的一个值，同时，样本x是随机的，所以频率派重点研究样本空间，大部分的概率计算都是针对样本x的分布。
贝叶斯派：待估计的参数θ是随机的，服从一定的分布，而样本x是固定的，由于样本是固定的，所以他们重点研究的是参数θ的分布。

3.2 LDA基础模型

w, 表示词语。V表示所有单词的个数(固定值)

z, 表示主题。K是主题的个数(预先设定的固定值)

D=(d1,d2,...,dm)表示语料库。其中m是语料库中的文档数

d=(w1,w2,...,wn)表示文档。其中n表示一篇文档中单词数(随机变量)

3.2.1 Unigram model一元模型

Unigram model假设文本中的词服从Multinomial分布

对于文档d=(w1,w2,...,wn)，用p(wn)表示词wn的先验概率，生成文档d的概率：

$p(d)=\prod _{n=1}^{N}p(w_{n})$

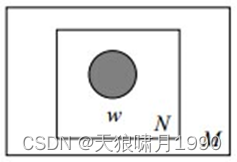
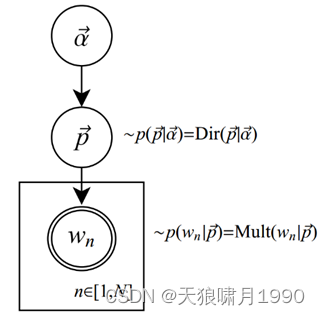
p是词服从Multinomial分布的参数

α是Dirichlet分布(即Multinomial分布的先验分布)的参数

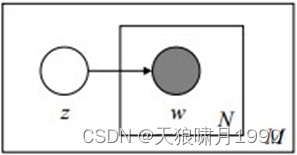
3.2.2 Mixture of unigrams model

该模型的生成过程：给某个文档选择一个主题z，再根据该主题生成文档，该文档中的所有词都来自一个主题。假设主题有z1,z2,...,zk，生成文档d的概率为：

$p(d)=p(z_{1}) \prod_{n=1}^{N}p(w_{n}|z_{1})+...+p(z_{k}) \prod_{n=1}^{N}p(w_{n}|z_{k}) \\ =\sum_{z}p(z)\prod_{n=1}^{N}p(w_{n}|z)$

3.3 pLSA模型(Probabilistic latent semantic analysis)

3.3.1 steps: pLSA得到"文档-词项"生成模型的步骤

p(di})--表示海量文档中某篇文档被选中的概率

p(wj|di)--表示词wj在给定文档di中出现的概率

p(zk|di)--表示某个主题zk在给定文档di下出现的概率

p(wj|zk)--表示具体某个词wj在给定主题zk下出现的概率，与主题关系越密切的词，其条件概率p(wj|zk)越大。

(1) 按照概率p(di)选择一篇文档di

(2) 选定文档di后，从主题分布中按照概率p(zk|di)选择一个隐含的主题类别zk

(3)选定zk后，从词语分布中按照概率p(wj|zk)选择一个词wj。

3.3.2 example: pLSA模型生成文档

requirement: 你要写M篇文档，每篇文档由不同的词组成。

condition: 由K个可供选择的主题，由V个可选的词。

(1)每写一篇文档，就制作一颗K面的"文档-主题"骰子，和K个V面的"主题-词项"骰子。比如：令K=3，V=3，得到

(2) 每写一个词，先扔该"文档-主题"骰子选择主题，得到主题结果后，使用和主题对应的那颗"主题-词项"骰子，扔该骰子选择要写的词。

主题分布：各个主题在文档d中出现的概率分布，比如{教育:0.5，经济:0.3，交通:0.2}，这是一个多项分布multi-nomial。

同理，词项分布也是一个多项分布。先从主题分布{教育：0.5，经济：0.3，交通：0.2}中抽取出主题：教育，然后从该教育主题对应的词分布{大学：0.5，老师：0.3，课程：0.2}中抽取出词：大学。

(3) 最后，重复扔"文档-主题"骰子和"主题-词项"骰子，重复N次(产生N个词)，完成一篇文档，重复这产生一篇文档的方法M词，就完成M篇文档。

3.3.3 Problem: 词袋模型，未关注词与词之间的顺序

3.3.4 Understanding: pLSA模型

pLSA模型假设一组共现(co-occurrence)词项关联着一个隐含的主题类别zk∈{z1,z2,...,zk}。即假定某个主题zk下单词wi容易和某个单词wj共同作用，形成共现，e.g. 小米加步枪。

3.3.5 根据文档反推其主题分布

这是主题建模的目的：自动地发现文档training set中的主题分布。

$p(wj|di) = \sum_{k=1}^{K}p(w_{j}|z_{k})p(z_{k}|d_{i})$

$p(d_{i}, w_{j}) = p(d_{i})p(w_{j}|d_{i}) \\ =p(d_{i})\sum_{k=1}^{K}p(w_{j}|z_{k})p(z_{k}|d_{i})$

由于p(di)和p(wj|di)可以事先算出，用EM算法估计pLSA模型的两个位置参数p(wj|zk)和p(zk|di)。

3.3.6 EM算法

Essence本质：先随机设置初始概率，然后通过期望求出贡献，用极大似然估计新的概率，最终在反复迭代后，概率值极大逼近真实概率。

EM算法的思想非常简单，分为两步：Expection-Step和Maximization-Step。

E-step主要通过观察数据和现有模型来估计参数，然后用这个估计的参数值来计算似然函数的期望。
M-step是寻找似然函数最大化时对应的参数。

由于EM算法保证在每次迭代之后似然函数都会增加，所以函数最终会收敛。

Example：假设有两枚硬币A和B，它们的随机抛掷结果如下如所示：

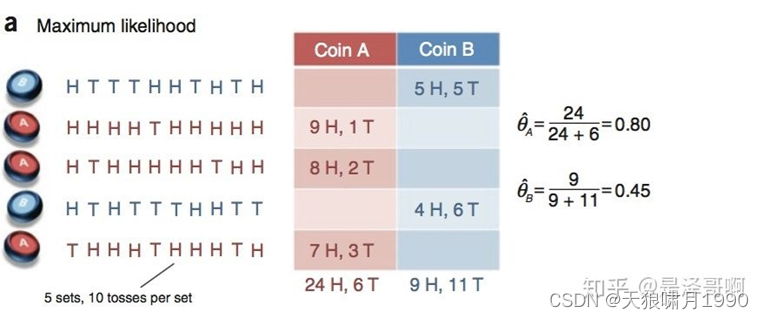
我们很容易估计出两枚硬币抛出正面的概率：

θA=0.8；θB=0.45

现在我们加入隐变量，抹去每轮投掷的硬币标记：

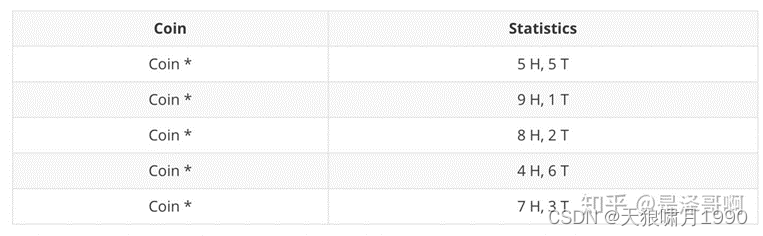
碰到这种情况，我们该如何估计θA和θB的值？

我们多了一个隐变量Z=(z1,z2,z3,z4,z5)，代表每一轮所使用的硬币，我们需要知道每一轮抛掷所使用的硬币这样才能估计θA和θB的值，但估计隐变量Z我们又需要知道θA和θB的值，才能用极大似然估计法去估计出Z。这样就陷入了一个鸡生蛋还是蛋生鸡的问题。

Solution：其解决办法就是先随机初始化θA和θB，然后用去估计Z，然后基于Z按照最大似然概率去估计新的θA和θB，循环至收敛。

随机初始化θA=0.6，θB=0.5。

对于第一轮来说，如果是硬币A，得出5正5反的概率为 $0.6^{5}*0.4^{5}$ ；如果是硬币B，得到 5 正 5 反的概率为： $0.5^{5}*0.5^{5}$ 。我们可以算出使用硬币A和使用硬币B的概率分别为：

$p_{A}=\frac{0.6^{5}*0.4^{5}}{(0.6^{5}*0.4^{5})+(0.5^{5}+0.5^{5})}=0.45$

$p_{B}=\frac{0.5^{5}+0.5^{5}}{(0.6^{5}+0.4^{5})+(0.5^{5}+0.5^{5})}=0.55$

3.3.6.1 E-step

从期望的角度来看，对于第一轮抛掷，使用硬币A的概率是0.45，使用硬币B的概率是0.55。同理其他轮。这一步我们实际上是估计出了Z的概率分布，这就是E-step。

结合硬币A的概率和上一张投掷结果，我们利用期望可以求出硬币A和硬币B的贡献。

H: 0.8*9=7.2

T: 0.8*1=0.8

3.3.6.2 M-step

然后用极大似然估计来估计新的θA 和θB。

$\theta'_{A}=\frac{21.3}{21.3+8.6}=0.71$

$\theta'_{B}=\frac{11.7}{11.7+8.4}=0.58$

这步就对应了M-step，重新估计出了参数值。

如此反复迭代，我们就可以算出最终的参数值。

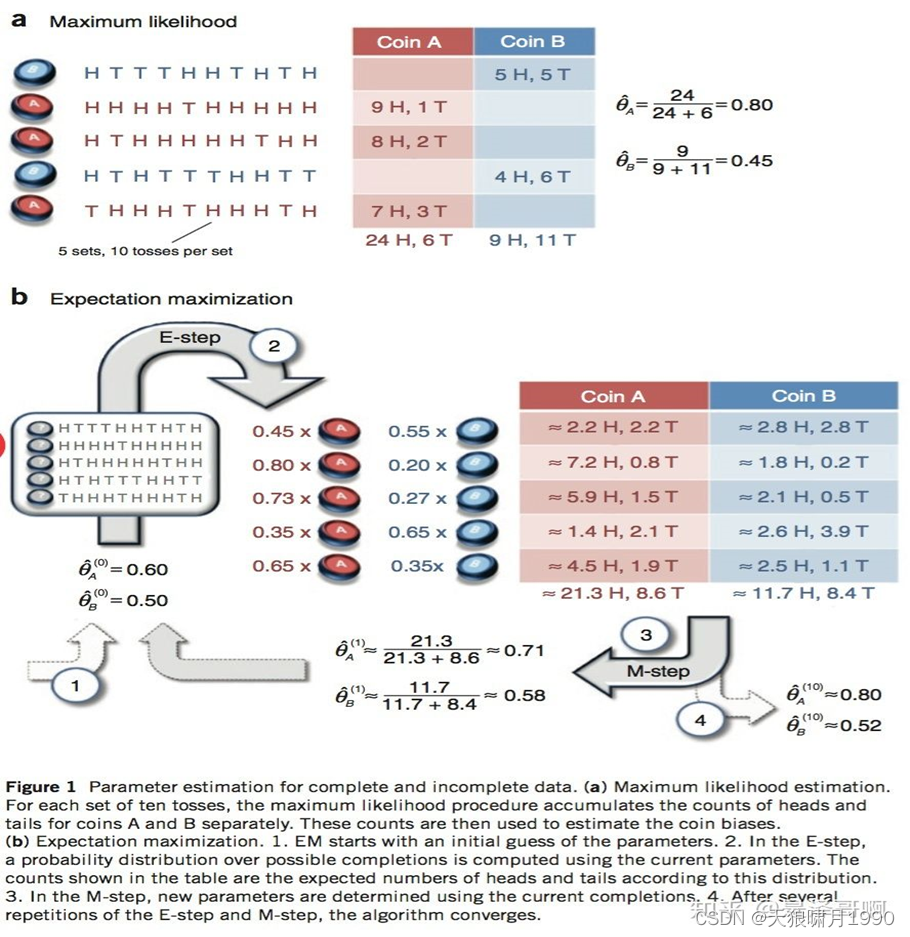
3.4 LDA模型生成文档过程

LDA就是在pLSA基础上加层贝叶斯框架，文档生成过程如下：

(1) 按照先验概率p(di)选择一篇文档。

(2) 从Dirichlet分布α中取样生成文档di的主题分布θi，即主题分布θi是由超参数α的Dirichlet分布生成的。

(3)从主题的多项式分布θi中取样生成文档di第j个词的主题Zi,j

(4) 从Dirichlet分布β中取样生成主题Zi,j对应的词语分布 $\Phi_{zi,j}$

(5) 从词语的多项式 $\Phi_{zi,j}$ 分布中采样最终生成词语Wi,j。

3.5 pLSA与LDA区别

(1) 生成文档过程不同

在pLSA中，主题分布和词分布是唯一确定的。{教育:0.5，交通:0.3}

在LDA中，主题分布和词分布不再是唯一确定的，而是由Dirichlet先验随机确定。可能是{教育:0.5，交通:0.3}，也可能是{教育:0.4，交通:0.4}

(2) 反推 -> 估计未知参数的方式不同

pLSA模型：EM算法

LDA：Gibbs采样

3.6 Gibbs采样

Essence本质：以条件概率 -> 模拟联合概率分布

条件：需要知道条件概率
思想：Gibbs采样是Markov Chain Monte Carlo(MCMC)的一种算法，MCMC借助Markov链的平稳分布特征模拟高维概率分布！

Gibbs采样是通过条件分布采样模拟联合分布，再通过模拟的联合分布直接推导出条件分布，以此循环。当Markov链经过burn-in阶段，消除初始参数的影响，到达平稳状态后，每一次状态转移都可以生成待模拟分布的一个样本。

e.g. 跳过初始的一定数量的单元(比如100个)，然后隔一定的数量取一个单元(比如隔20个取一个)，这样sample的单元是逼近联合分布的。

意义：多维/高维(2维以上)积分、期望或联合分布是很难计算的，这时才需要Gibbs采样，得到近似解！
例子：

甲只能；E：吃饭、学习、打球，
时间；T：上午、下午、晚上，
天气；W：晴朗、刮风、下雨。
现在要一个sample，这个sample可以是：打球+下午+晴朗。

Condition：p(E|T,W),p(T|E,W),p(W|E,T)。现在要做的就是通过这三个已知的条件分布，再用gibbs sampling的方法，得到联合分布。

首先随便初始化一个组合,i.e. 学习+晚上+刮风，
然后依条件概率改变其中的一个变量。
具体说，假设我们知道晚上+刮风，我们给E生成一个变量，比如，学习-》吃饭。我们再依条件概率改下一个变量，根据学习+刮风，把晚上变成上午。类似地，把刮风变成刮风（当然可以变成相同的变量）。这样学习+晚上+刮风->吃饭+上午+刮风。

同样的方法，得到一个序列，每个单元包含三个变量，也就是一个马尔可夫链。然后跳过初始的一定数量的单元（比如100个），然后隔一定的数量取一个单元（比如隔20个取1个）。这样sample到的单元，是逼近联合分布的。

4. LDA codes

4.1 LDA implementation 1

github address: topic_models/LDA-demo at master · laserwave/topic_models · GitHub

python-codes package编解码包

codes.encode(obj, encoding='utf-8', errors='strict')，使用encoding指定的编解码器对obj进行编码，类似str.encode()方法

codes.decode(obj, encoding='utf-8', errors='strict')，使用encoding指定的编解码器对obj进行解码，类似str.decode()方法

4.2 LDA implementation 2

github address: git@github.com:DengYangyong/LDA_gensim.git

常用函数：

genism.doc2bow()方法，转化为单一向量。该方法只考虑词频，不考虑词语间的位置关系。

(1) slice。将分词后的字符串文档切分成词语列表。

(2) 构建词典dictionary。词典是所有文档所有单词的集合，并且记录了各词的出现次数。 <- 将词语映射到数字+只考虑词频。

Dictionary = corpora.Dictionary(text)

(3) 生成词典后，将其转化为向量形式。

Corpus = [dictionary.doc2bow(text) for text in texts]

<- genism内部用稀疏矩阵表示。因为单词总量极大，而一篇文档单词数有限，用密集矩阵来表示的话造成内存浪费。

4.3 Ida2vec implementation

essence本质：word2vec + document representation vector(来自于LDA而非paragraph vector)

LDA: topic distribution * each document's topic probability =each document representation vector

each topic vector is similar to word vectors in the same space

document vector is a weighted sum of topic vectors

lda2vec {word2vec: model word-to-word relationships

{LDA: model document-to-word relationships

Reference: GitHub - cemoody/lda2vec

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/羊村懒王/article/detail/361009