动力学约束下的运动规划算法——Kinodynamic RRT*算法

   为了更好的理解Kinodynamic RRT*算法，我们先来回顾一下RRT * 算法

---

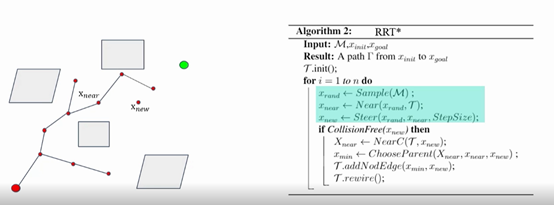
   RRT * 先通过Sample函数随机选取一个点Xrand，然后通过Near函数找到当前树上距离Xrand最近的一个点Xnear，再通过Steer函数，沿着从Xnear到Xrand的方向走一步，步长为Stepsize，得到一个点Xnew

   与RRT不同的是，在得到Xnew后不是直接将Xnew与Xnear连起来，而是通过NearC函数在以Xnew为圆心的，R为半径的圆的区域内去找到Xnew附近的一些节点，如上图中的Xnear、X1、X2

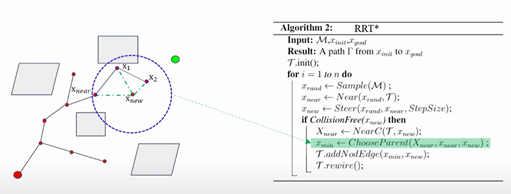
   然后通过ChooseParent函数，将Xnew将这些点连接起来，分别计算从起点到Xnew的这三条路径哪一个花费是比较小的，这里的花费可以选为路径最短，也可以选择其他标准，上图中的例子中通过Xnear到达Xnew的那条路是最短的，这个时候Xnear就被选作了Xnew的父节点，如下图所示

   然后通过rewire函数去优化路径，将X1和X2分别与Xnew相连，去判断原来从起始点到X1的路更好，还是现在经过Xnew到X1的路更好，这里采用的衡量标准是路径长度，显然对于X1而言，是原来的路更短，不做处理，对于X2而言，显然是经过Xnew的路更短，因此将X2的父节点更改为Xnew，如下图所示：

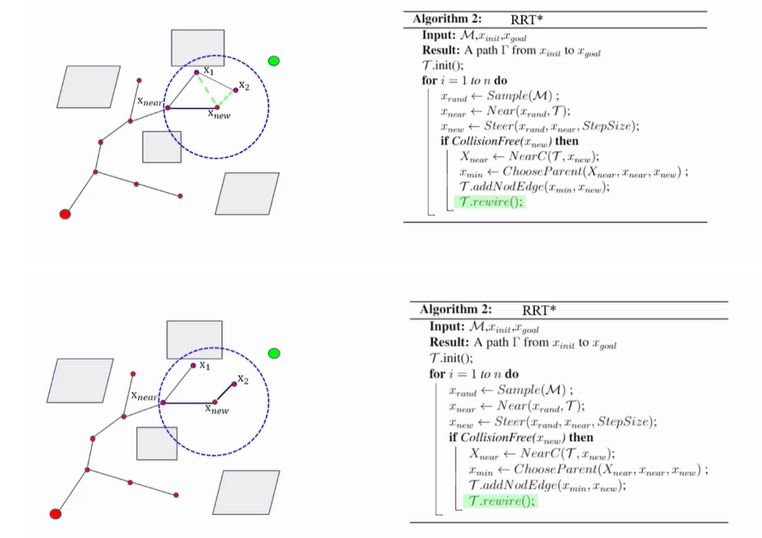
   除此之外，相对于RRT算法，RRT*在找到一条从起点到终点的路径后并没有停止，而是不断的优化，所以说RRT * 是一种渐进最优的算法，而RRT是一种非最优的算法

---

   基于上面对RRT * 算法的回顾，接下来我们来看一下Kinodynamic RRT * 算法与传统的RRT * 算法有哪些不同

---

   1、采样——Sample

   传统的RRT * 算法在采样时在欧几里德空间中仅对位置进行采样，而Kinodynamic RRT * 算法是在全状态空间中采样。比如，针对位置、速度进行采样。

---

   2、寻找RRT树上最"邻近"节点——Near

   与传统的RRT * 算法不同，Kinodynamic RRT*算法在寻找最"邻近"节点时，不能仅考虑位置上最接近，而是需要考虑动力学约束，所以个人认为这里的最“邻近”节点，可以理解成到新节点连接代价值最小的节点。

   上述过程中需要求解两个节点间的轨迹，即两点边界值问题BVP、或最优两点边界值问题OBVP。该问题可以通过前文介绍的庞特里亚金最小值原理进行求解，链接如下：

   动力学约束下的运动规划算法——两点边界值最优控制问题 OBVP

   提出Kinodynamic RRT*算法的作者在论文中给出了另一种求解该问题的方法，下面对该方法进行介绍。若不关心该方法，可略过该部分，直接跳到第3条

   如果引入最优控制，我们可以定义如下的状态转移代价函数(通常采用二次型的时间-能量最优，即希望能量花费最小，并且耗费的时间要尽可能的小)
   $$c[\pi ]={\int }_0^{\tau }\left(1+u(t{)}^{T}Ru(t)\right)dt$$

   如果从一种状态转移到另一种状态的成本很小，那么两种状态就很接近。(注意，如果反向转移，费用可能不同)

   如果已知转移的到达时间τ和转移的控制策略u(t)，就可以计算出转移的成本，这是经典的最优控制解(OBVP)

   （1）情况1：固定的最终状态x1，固定的最终时间τ

   此时，最优控制策略$u^{\ast }(t)$如下所示：

   $$u^{\ast }(t)=R^{-1}{B}^T\exp [A^T(\tau -t)]G(\tau {)}^{-1}[x_1-\bar{x}(\tau )].$$
   其中，