【强化学习】常用算法之一 “DQN”_dqn公式
赞
踩
持续分享：机器学习、深度学习、python相关内容、日常BUG解决方法及Windows&Linux实践小技巧。
如发现文章有误，麻烦请指出，我会及时去纠正。有其他需要可以私信我或者发我邮箱:zhilong666@foxmail.com
强化学习是机器学习中的一大分支，通过与环境的交互，通过不断试错来学习如何做出最优决策。Deep Q-Network(DQN)算法是强化学习中的经典算法之一，它结合了深度学习和Q-learning算法，可以在宽泛的任务领域中学习和解决问题。
本文将详细讲解强化学习常用算法之一“DQN”
目录
一、简介
DQN算法是深度学习领域首次广泛应用于强化学习的算法模型之一。它于2013年由DeepMind公司的研究团队提出，通过将深度神经网络与经典的强化学习算法Q-learning结合，实现了对高维、连续状态空间的处理，具备了学习与规划的能力。
二、发展史
在DQN算法提出之前，强化学习中的经典算法主要是基于表格的Q学习算法。这些算法在处理简单的低维问题时表现出色，但随着状态和动作空间的增加，表格表示的存储和计算复杂度呈指数级增长。为了解决这个问题，研究人员开始探索使用函数逼近的方法，即使用参数化的函数代替表格。
之后，逐步发展出了一系列将深度学习应用于强化学习的算法。DQN算法是其中的一种。它是由Alex Krizhevsky等人在2013年提出的，是首个将深度学习与强化学习相结合的算法。DQN算法引入了经验回放和固定Q目标网络等技术，极大地提升了深度神经网络在强化学习中的性能。随后，DQN算法在Atari游戏中取得了比人类玩家更好的成绩，引起了广泛的关注和研究。
-
Q-learning：Q-learning是强化学习中的经典算法，由Watkins等人在1989年提出。它使用一个Q表格来存储状态和动作的价值，通过不断更新和探索来学习最优策略。然而，Q-learning算法在面对大规模状态空间时，无法扩展。
-
Deep Q-Network(DQN)：DQN算法在2013年由DeepMind团队提出，通过使用深度神经网络来逼近Q函数的值，解决了状态空间规模大的问题。该算法采用了两个关键技术：经验回放和固定Q目标网络。
-
经验回放：经验回放是DQN算法的核心思想之一，它的基本原理是将智能体的经验存储在一个回放记忆库中，然后随机从中抽样，利用这些经验进行模型更新。这样做的好处是避免了样本间的相关性，提高了模型的稳定性和收敛速度。
-
固定Q目标网络：DQN算法使用两个神经网络，一个是主网络(online network)，用于选择动作，并进行模型更新；另一个是目标网络(target network)，用于计算目标Q值。目标网络的参数固定一段时间，这样可以减少目标的波动，提高模型的稳定性。
三、算法公式
DQN算法的核心是Q-learning算法和深度神经网络的结合。
1. Q-learning算法公式：
Q-learning算法通过不断更新Q值来学习最优策略，其更新公式如下：
其中，s_t表示当前状态，a_t表示选择的动作，r_t表示立即回报，s_t+1表示下一个状态，α是学习率，γ是折扣因子。
2. 深度神经网络：
DQN算法使用深度神经网络拟合Q函数的值。输入是状态s，输出是不同动作的Q值。常用的神经网络结构是多层感知机(MLP)或卷积神经网络(CNN)，通过训练来优化网络参数。网络的输出大小与动作空间的维度相同。
3. DQN算法公式：
DQN算法通过最小化Q函数的均方差损失来进行模型更新。其更新公式如下：
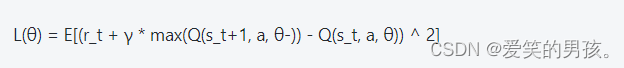
其中，θ是网络参数，Q(s_t, a, θ-)表示目标网络的输出。
四、算法原理
DQN算法的原理是通过利用深度神经网络逼近Q函数的值，实现对高维、连续状态空间的处理。其核心思想是通过不断更新神经网络的参数，使其的输出Q值逼近真实的Q值，从而学习最优策略。
DQN算法的工作原理如下：
-
初始化：初始化主网络和目标网络的参数。
-
选择动作：根据当前状态s，使用ε-greedy策略选择动作a。
-
执行动作并观察回报：采取动作a，与环境交互，观察下一个状态s’和立即回报r。
-
存储经验：将(s, a, r, s’)存储到经验回放记忆库中。
-
从经验回放记忆库中随机抽样：从记忆库中随机抽样一批经验。
-
计算目标Q值：使用目标网络计算目标Q值，即max(Q(s’, a, θ-))。
-
更新主网络：根据损失函数L(θ)进行模型参数更新。
-
更新目标网络：定期更新目标网络的参数。
-
重复步骤2-8，直到达到终止条件。
五、算法功能
DQN算法具有以下功能：
-
处理高维、连续状态空间：通过深度神经网络的逼近能力，可以处理高维、连续状态空间的问题。
-
学习和规划能力：通过与环境的交互和不断试错，DQN算法可以学习到最优策略，并具备一定的规划能力。
-
稳定性和收敛速度高：DQN算法通过经验回放和固定Q目标网络等技术，提高了模型的稳定性和收敛速度。
六、示例代码
以下是一个使用DQN算法解决经典的CartPole问题的示例代码：
- # -*- coding: utf-8 -*-
- import gym
- import numpy as np
- from tensorflow.keras.models import Sequential
- from tensorflow.keras.layers import Dense
- from tensorflow.keras.optimizers import Adam
-
- env = gym.make('CartPole-v0')
- n_actions = env.action_space.n
- n_states = env.observation_space.shape[0]
-
- def create_dqn_model():
- model = Sequential()
- model.add(Dense(32, input_shape=(n_states,), activation='relu'))
- model.add(Dense(32, activation='relu'))
- model.add(Dense(n_actions, activation='linear'))
- model.compile(loss='mse', optimizer=Adam(lr=0.001))
- return model
-
- def choose_action(state, epsilon):
- if np.random.rand() < epsilon:
- return np.random.choice(n_actions)
- else:
- q_values = model.predict(state)
- return np.argmax(q_values[0])
-
- def train_dqn():
- epsilon = 1.0
- epsilon_min = 0.01
- epsilon_decay = 0.995
- batch_size = 32
- replay_memory = []
- for episode in range(500):
- state = env.reset()
- state = np.reshape(state, [1, n_states])
- done = False
- steps = 0
-
- while not done:
- env.render()
- action = choose_action(state, epsilon)
- next_state, reward, done, _ = env.step(action)
- next_state = np.reshape(next_state, [1, n_states])
- replay_memory.append((state, action, reward, next_state, done))
- state = next_state
- steps += 1
-
- if done:
- print("Episode: %d, Steps: %d" % (episode, steps))
- break
- if len(replay_memory) > batch_size:
- minibatch = np.random.choice(replay_memory, batch_size, replace=False)
- states_mb = np.concatenate([mb[0] for mb in minibatch])
- actions_mb = np.array([mb[1] for mb in minibatch])
- rewards_mb = np.array([mb[2] for mb in minibatch])
- next_states_mb = np.concatenate([mb[3] for mb in minibatch])
- dones_mb = np.array([mb[4] for mb in minibatch])
-
- targets = rewards_mb + 0.99 * (np.amax(model.predict_on_batch(next_states_mb), axis=1)) * (1 - dones_mb)
- targets_full = model.predict_on_batch(states_mb)
- ind = np.array([i for i in range(batch_size)])
- targets_full[[ind], [actions_mb]] = targets
-
- model.fit(states_mb, targets_full, epochs=1, verbose=0)
-
- if epsilon > epsilon_min:
- epsilon *= epsilon_decay
-
- env.close()
-
- if __name__ == '__main__':
-
- model = create_dqn_model()
-
- train_dqn()
运行结果：
Episode: 0, Steps: 14
Episode: 1, Steps: 26
Episode: 2, Steps: 16
Episode: 3, Steps: 12
Episode: 4, Steps: 12
...
Episode: 498, Steps: 160
Episode: 499, Steps: 200
通过运行以上代码，可以看到DQN算法在解决CartPole问题上的表现。在经过多个episode的训练后，算法可以在游戏中坚持更久的时间，最终取得较高的得分。
七、总结
本文对DQN算法进行了详细的讲解，包括发展史、算法公式和原理、功能、示例代码以及如何使用。DQN算法通过结合深度学习和Q-learning算法，实现了对高维、连续状态空间的处理，具备了学习和规划的能力。通过示例代码的运行结果，我们可以看到DQN算法在解决CartPole问题上取得了较好的效果。然而，DQN算法也存在一些局限性，比如训练不稳定、样本相关性等问题。未来的研究可以进一步改进算法，并将其应用于更广泛的任务领域。
