【C语言 - 哈希表 - 力扣 - 相交链表】_相交链表输入案例

相交链表题目描述

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表不存在相交节点，返回 null 。
图示两个链表在节点 c1 开始相交：

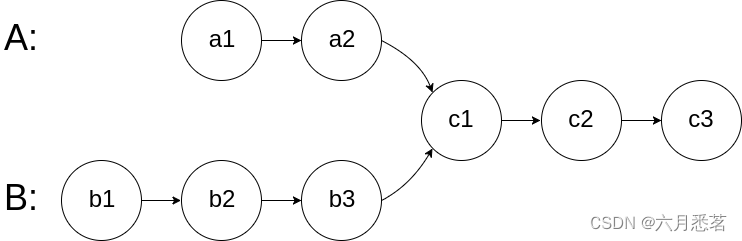
题目数据 保证 整个链式结构中不存在环。

注意，函数返回结果后，链表必须 保持其原始结构 。

自定义评测：
评测系统 的输入如下（你设计的程序 不适用 此输入）：

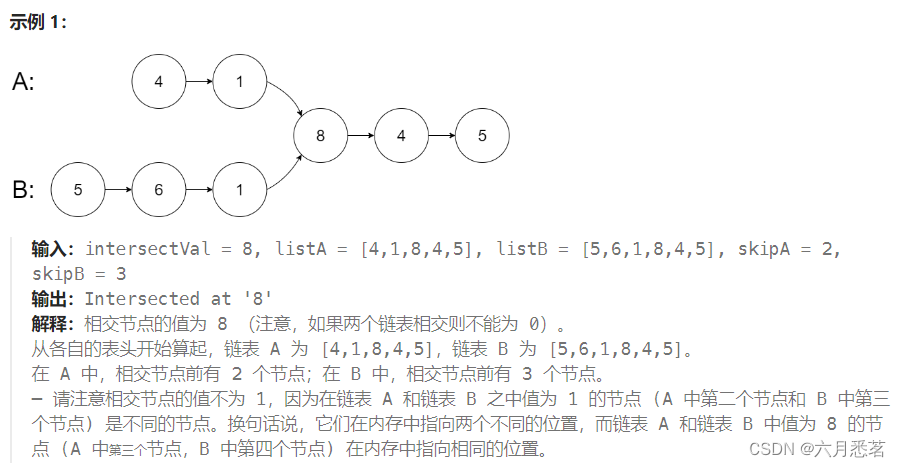
intersectVal - 相交的起始节点的值。如果不存在相交节点，这一值为 0
listA - 第一个链表
listB - 第二个链表
skipA - 在 listA 中（从头节点开始）跳到交叉节点的节点数
skipB - 在 listB 中（从头节点开始）跳到交叉节点的节点数
评测系统将根据这些输入创建链式数据结构，并将两个头节点 headA 和 headB 传递给你的程序。如果程序能够正确返回相交节点，那么你的解决方案将被 视作正确答案 。

题解

方法一：哈希集合

判断两个链表是否相交，可以使用哈希集合存储链表节点。

首先遍历链表 headA，并将链表 headA 中的每个节点加入哈希集合中。然后遍历链表 headB，对于遍历到的每个节点，判断该节点是否在哈希集合中：

如果当前节点不在哈希集合中，则继续遍历下一个节点；

如果当前节点在哈希集合中，则后面的节点都在哈希集合中，即从当前节点开始的所有节点都在两个链表的相交部分，因此在链表 headB 中遍历到的第一个在哈希集合中的节点就是两个链表相交的节点，返回该节点。

如果链表 headB 中的所有节点都不在哈希集合中，则两个链表不相交，返回 null。

// 定义哈希表结构体
struct HashTable {
    struct ListNode *key; // 哈希表的键，指向链表节点
    UT_hash_handle hh;    // 哈希表的特殊域，用于管理哈希表
};

// 函数：获取两个链表的交点
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    // 初始化哈希表
    struct HashTable *hashTable = NULL;
    // 遍历链表 headA，将节点添加到哈希表中
    struct ListNode *temp = headA;
    while (temp != NULL) {
        // 临时指针
        struct HashTable *tmp;
        // 在哈希表中查找当前节点是否存在
        HASH_FIND(hh, hashTable, &temp, sizeof(struct HashTable *), tmp);
        // 如果节点不存在于哈希表中，则将其加入哈希表
        if (tmp == NULL) {
            tmp = malloc(sizeof(struct HashTable));
            tmp->key = temp;
            HASH_ADD(hh, hashTable, key, sizeof(struct HashTable *), tmp);
        }
        // 继续遍历下一个节点
        temp = temp->next;
    }
    // 遍历链表 headB，查找是否存在于哈希表中的节点
    temp = headB;
    while (temp != NULL) {
        // 临时指针
        struct HashTable *tmp;
        // 在哈希表中查找当前节点是否存在
        HASH_FIND(hh, hashTable, &temp, sizeof(struct HashTable *), tmp);
        // 如果找到了交点，则直接返回该节点
        if (tmp != NULL) {
            return temp;
        }
        // 继续遍历下一个节点
        temp = temp->next;
    }
    // 如果遍历完链表 headB 都没有找到交点，则返回 NULL
    return NULL;
    // 这种方法利用了哈希表的快速查找特性，将时间复杂度从线性降低到了接近常数级别。
    // 总体而言，这段代码展示了哈希表在解决链表相关问题中的应用，特别是在寻找交点等场景下能够提供高效的解决方案。
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46

哈希表

哈希表（Hash Table），也称为散列表，是一种常用的数据结构，用于实现关联数组。它通过将键（key）映射到数组（Array）的特定位置来实现快速的数据检索。哈希表的主要思想是利用哈希函数将键转换为数组索引，然后将值存储在该索引位置的数组中。

哈希表的基本结构包括以下几个重要组成部分：

1. 哈希函数（Hash Function）：哈希函数是哈希表的核心，它负责将键映射到数组的特定位置。良好的哈希函数应该具有以下特性：

   • 易于计算：哈希函数应该能够快速计算出哈希值。
   • 均匀分布：哈希函数应该能够将键均匀地分布在数组中，以减少冲突的发生。
   • 最小冲突：哈希函数应该能够尽量减少键的冲突，即不同的键映射到相同的数组索引的情况。

2. 数组（Array）：哈希表使用数组来存储键值对。每个数组位置称为“桶”（Bucket），一个桶可以存储一个或多个键值对。当发生哈希冲突时，通常使用一种解决冲突的方法来处理，比如链地址法或开放地址法。

3. 解决冲突的方法：由于不同的键可能会映射到相同的数组索引位置，所以哈希表需要一种解决冲突的方法。常见的方法包括：

   • 链地址法（Chaining）：将具有相同哈希值的键值对存储在同一个桶中的链表或其他数据结构中。
   • 开放地址法（Open Addressing）：当发生冲突时，通过探查数组中的其他位置来寻找空闲的位置，并将键值对插入到空闲位置中。

哈希表的时间复杂度取决于哈希函数的性能和冲突解决方法的效率。在理想情况下，哈希表可以实现常数时间复杂度的查找、插入和删除操作（O(1)），但在最坏情况下，可能会退化到线性时间复杂度（O(n)）。

哈希表被广泛应用于各种编程语言的标准库中，用于实现诸如字典（Dictionary）、集合（Set）等数据结构，以及在数据库中用于加快数据检索速度等场景。

方法二：双指针

思路和算法

使用双指针的方法，可以将空间复杂度降至 O(1)。

只有当链表 headA 和 headB 都不为空时，两个链表才可能相交。因此首先判断链表 headA 和 headB 是否为空，如果其中至少有一个链表为空，则两个链表一定不相交，返回 null。

当链表 headA 和 headB 都不为空时，创建两个指针 pA 和 pB，初始时分别指向两个链表的头节点 headA 和 headB，然后将两个指针依次遍历两个链表的每个节点。具体做法如下：

每步操作需要同时更新指针 pA 和 pB。

如果指针 pA 不为空，则将指针 pA 移到下一个节点；如果指针 pB 不为空，则将指针 pB 移到下一个节点。

如果指针 pA 为空，则将指针 pA 移到链表 headB 的头节点；如果指针 pB 为空，则将指针 pB 移到链表 headA 的头节点。

当指针 pA 和 pB 指向同一个节点或者都为空时，返回它们指向的节点或者 null。

证明

下面提供双指针方法的正确性证明。考虑两种情况，第一种情况是两个链表相交，第二种情况是两个链表不相交。

情况一：两个链表相交

链表headA 和 headB 的长度分别是 m 和 n。假设链表 headA 的不相交部分有 a 个节点，链表 headB 的不相交部分有 b 个节点，两个链表相交的部分有 c 个节点，则有 a+c=m，b+c=n。

如果 a=b，则两个指针会同时到达两个链表相交的节点，此时返回相交的节点；

如果 a≠b，则指针 pA 会遍历完链表 headA，指针 pB 会遍历完链表 headB，两个指针不会同时到达链表的尾节点，然后指针 pA 移到链表 headB 的头节点，指针 pB 移到链表 headA 的头节点，然后两个指针继续移动，在指针 pA 移动了 a+c+b 次、指针 pB 移动了 b+c+a 次之后，两个指针会同时到达两个链表相交的节点，该节点也是两个指针第一次同时指向的节点，此时返回相交的节点。

情况二：两个链表不相交

链表 headA 和 headB 的长度分别是 m 和 n。考虑当 m=n 和 m≠n 时，两个指针分别会如何移动：

如果 m=n，则两个指针会同时到达两个链表的尾节点，然后同时变成空值 null，此时返回 null；

如果 m≠n，则由于两个链表没有公共节点，两个指针也不会同时到达两个链表的尾节点，因此两个指针都会遍历完两个链表，在指针 pA 移动了 m+n 次、指针 pB 移动了 n+m 次之后，两个指针会同时变成空值 null，此时返回 null。

// 函数：获取两个链表的交点
struct ListNode *getIntersectionNode(struct ListNode *headA, struct ListNode *headB) {
    // 如果其中一个链表为空，则直接返回 NULL，因为没有交点
    if (headA == NULL || headB == NULL) {
        return NULL;
    }
    // 初始化两个指针 pA 和 pB 分别指向链表 headA 和 headB 的头节点
    struct ListNode *pA = headA, *pB = headB;
    // 当 pA 不等于 pB 时循环，即两个指针没有相遇
    while (pA != pB) {
        // 如果 pA 到达了链表 headA 的末尾，则将 pA 指向链表 headB 的头节点
        pA = pA == NULL ? headB : pA->next;
        // 如果 pB 到达了链表 headB 的末尾，则将 pB 指向链表 headA 的头节点
        pB = pB == NULL ? headA : pB->next;
    }
    // 返回 pA（或 pB），即两个链表的交点，如果没有交点则返回 NULL
    return pA;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

帮助理解

将2个链表在末尾加上对方，碰到第一个相同的点，要么是交点，要么是末尾

situation 1

A: 1 -> 2 -> 3 -> C -> 4 -> 5 -> null

B: 6 -> 7 -> C -> 4 -> 5 -> null

A + B: 1 -> 2 -> 3 -> C -> 4 -> 5 -> 6 -> 7 -> C -> 4 -> 5 -> null

B + A: 6 -> 7 -> C -> 4 -> 5 -> 1 -> 2 -> 3 -> C -> 4 -> 5 -> null

situation 2

A: 1 -> 2 -> 3 -> 4 -> 5 -> null

B: 6 -> 7 -> 8 -> 3 -> null

A + B: 1 -> 2 -> 3 -> 4 -> 5 -> 6 -> 7 -> 8 -> 3 -> null

B + A: 6 -> 7 -> 8 -> 3 -> 1 -> 2 -> 3 -> 4 -> 5 -> null

作者：力扣官方题解
链接：https://leetcode.cn/problems/intersection-of-two-linked-lists/solutions/811625/xiang-jiao-lian-biao-by-leetcode-solutio-a8jn/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。