智能优化算法--差分进化算法_差分进化算法原理

1、算法简介

在遗传、选择和变异的作用下，自然界生物体优胜劣汰，不断由低级向高级进化和发展。基于这个原理，人们提出了差分进化算法。

差分进化算法基于群体智能理论，是通过群体内个体间的合作与竞争而产生的智能优化搜索算法。

差分进化算法特点：

（1）结构简单，容易使用。主要通过差分变异算子来进行遗传操作。

（2）性能优越。具有较好的可靠性，鲁棒性，高效性。

（3）自适应性。差分变异算子可以是一个常数，也可以是一个具有变异步长和搜索方向的自适应能力。

（4）具有内在并行性，可协同搜索。在同一要求下，差分进化算法拥有更快的收敛速度。

2、算法原理

基本差分进化算法的操作程序如下：

（1）初始化；

（2）变异；

（3）交叉；

（4）选择；

（5）边界条件处理。

（1）初始化

差分进化算法利用 $N_p$ 个维数为 D 的实数值参数向量，将它们作为每一代的种群，每个个体表示为

$${\mathbf{x}}_{i,G}\left(i=1,2,\cdots ,N_{\mathrm{P}}\right)$$

一般假定所有随机初始化种群均符合均匀概率分布，设参数变量的界限为，

$$x_j^{(L)}<x_j<x_j^{(U)}$$
则

$$x_{ji,0}=\mathrm{rand}[0,1]\cdot \left(x_j^{(U)}-x_j^{(L)}\right)+x_j^{(L)}\left(i=1,2,\cdots ,N_{\mathrm{P}};j=1,2,\cdots ,D\right)$$

（2）变异

对于每个目标向量 ${\mathbf{x}}_{i,G}\left(i=1,2,\cdots ,N_{\mathrm{P}}\right)$ ，基本差分进化算法的变异向量由下式产生：

$${\mathbf{v}}_{i,G+1}={\mathbf{x}}_{r_1,G}+F\cdot \left({\mathbf{x}}_{r_2,G}-{\mathbf{x}}_{r_3,G}\right)$$
式中：

随机选择的序号r1、r2和r3互不相同，且r1、r2和r3与目标向量序号 i 也应不同，即 r1、r2、r3、i 互不相等。

变异算子 F∈［0，2］是一个实常数因数，

（3）交叉

为了增加干扰参数向量的多样性，引入交叉操作，则试验向量变为

u i , j + 1 = ( u 1 i , G + 1 , u 2 i , G + 1 , … , u D i , G + 1 ) u j i , G + 1 = { v j i , G + 1 ,  if  randb ⁡ ( j ) ≤ C R  or  j = rnbr ⁡ ( i ) u j i , G + 1 ,  else  i = 1 , 2 , … , N P ; j = 1 , 2 , … , D

$$\begin{aligned} &u_{i, j+1}=\left(u_{1 i, G+1}, u_{2 i, G+1}, \ldots, u_{D i, G+1}\right) \\ &u_{j i, G+1}=\left\{\begin{array}{l} v_{j i, G+1}, \text { if } \operatorname{randb}(j) \leq CR \text { or } j=\operatorname{rnbr}(i) \\ u_{j i, G+1}, \text { else } \end{array}\right. \\ &i=1,2, \ldots, N_P ; j=1,2, \ldots, D \end{aligned}$$ ​ui,j+1​=(u1i,G+1​,u2i,G+1​,…,uDi,G+1​)uji,G+1​={vji,G+1​, if randb(j)≤CR or j=rnbr(i)uji,G+1​, else ​i=1,2,…,NP​;j=1,2,…,D​
randb(j)表示产生[0,1]之间随机数第 j 个估计值；rnbr 表示一个随机选择的序列，范围是 0 ~ D；CR ∈［0，1]是交叉算子。

通俗理解就是如果随机产生的 randb(j) 小于 CR 或者 j=r ,那么就将变异后的种群放入选择群体中，如果不是就就将原来的种群放入选择种群中。

（4）选择

为决定试验向量 $u_{i,G+1}$ 是否会成为下一代中的成员，差分进化算法按照贪婪准则将试验向量与当前种群中的目标向量 $x_{i,G+1}$ 进行比较。如果目标函数要被最小化，那么具有较小目标函数值的向量将在下一代种群中出现。下一代中的所有个体都比当前种群的对应个体更佳或者至少一样好。

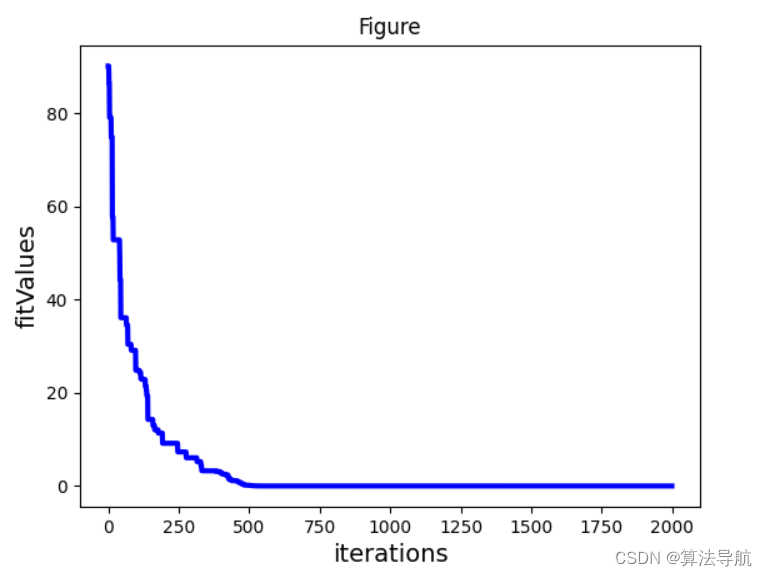
3、仿真实例

计算 $f(x)={\sum }_{i=1}^n{x}_i^2-10cos(2\pi x_i)+10$ 最小值

# @Time : 2021/11/18 10:20
# @Author : xiao cong
# @Function :
"""
基本差分进化算法的操作程序如下：
（1）初始化；
（2）变异；
（3）交叉；
（4）选择；
（5）边界条件处理。
"""
import numpy as np
import matplotlib.pyplot as plt


class DE:

    # 初始化变量
    def __init__(self, pN, dim, generation):
        self.pN = pN  # 种群大小
        self.F = 0.6
        self.CR = 0.7
        self.generation = generation  # 迭代次数
        self.dim = dim  # 维度
        self.valueDownRange = -5.12  # 下界
        self.valueUpRange = 5.12
        self.X = np.random.uniform(self.valueDownRange, self.valueUpRange, size=(self.pN, self.dim))  # 初始化目标种群
        self.V = np.zeros((self.pN, self.dim))  # 变异种群
        self.U = np.zeros((self.pN, self.dim))  # 试验种群

    # 目标函数
    def function(self, x_list):
        f = 0.0
        for i in range(len(x_list)):
            f = f + x_list[i] ** 2 - 10 * np.cos(2 * np.pi * x_list[i]) + 10
        return np.float(f)

    # 变异
    def mutation(self):
        for i in range(self.pN):
            r1, r2, r3 = 0, 0, 0
            while r1 == r2 or r2 == r3 or r3 == r1 or r1 == i or r2 == i or r3 == i:
                r1 = np.random.randint(0, self.pN)
                r2 = np.random.randint(0, self.pN)
                r3 = np.random.randint(0, self.pN)
            self.V[i] = self.X[r1, :] + self.F * (self.X[r2, :] - self.X[r3, :])

        return self.V

    # 交叉
    def crossover(self):
        for i in range(self.pN):
            jrand = np.random.randint(0, self.dim)
            r = np.random.random()

            for j in range(self.dim):
                if r <= self.CR or j == jrand:
                    self.U[i][j] = self.V[i][j]
                else:
                    self.U[i][j] = self.X[i][j]

        return self.U

    # 选择
    def selection(self):
        for i in range(self.pN):
            if self.function(self.U[i]) <= self.function(self.X[i]):
                self.X[i] = self.U[i]

        return self.X

    # 迭代
    def run(self):
        fitValues = []
        fitX = []

        for i in range(self.generation):
            self.mutation()
            self.crossover()
            self.selection()

            values = []
            for n in range(self.pN):
                values.append(self.function(self.X[n, :]))
            fitValues.append(min(values))  # 记录每次迭代适应度
            fitX.append(self.X[np.array(values).argmin()])  # 记录取最值时的变量值

        return fitX, fitValues


myDE = DE(pN=100, dim=10, generation=2000)
fitX, fitValues = myDE.run()


print("最终迭代值 = ", fitValues[-1])
print("此时自变量值为", fitX[-1])

# 绘图
iterations = np.arange(0, 2000)
plt.plot(iterations, fitValues, color='b', linewidth=3)
plt.title("Figure")
plt.xlabel("iterations", size=14)
plt.ylabel("fitValues", size=14)
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104