深入浅出Transformer(一)_transformer模型 深入浅出

引言

Transformer的重要性不用多说了吧，NLP现在最火了两个模型——BERT和GPT，一个是基于它的编码器实现的，另一个是基于它的解码器实现的。

凡是我不能创造的，我都不能理解。

为了更好的理解Transformer¹模型，我们需要知道它的实现细节。本文我们就如庖丁解牛一般，剖析它的原理与实现细节——通过Pytorch实现。

为了更好的理解Transformer，英文阅读能力好的建议先看一下它的原始论文¹,以及两篇非常好的解释文章(这里和这里)。本文会结合这些文章的内容，争取阐述清楚每个知识点。由于内容有点多，可能会分成三篇文章。

为了方便，本文把原文的翻译结果也贴出来，翻译放到引用内。

背景

$这是原文翻译$ 循环神经网络，尤其是LSTM和GRU，一直以来都在序列建模和转导问题(比如语言模型和机器翻译)上保持统治地位。此后，人们不断努力提升循环网络语言模型和编码器-解码器结构的瓶颈。

循环模型通常是对输入和输出序列的符号位置进行因子计算。在计算期间对齐位置和时间步，基于前一时间步的隐藏状态$h_{t-1}$和当前时间步$t$的输入，循环生成了一系列隐藏状态$h_t$。这种固有的顺序特性排除了训练的并行化，这在更长的序列中成为重要问题，因为有限的内存限制了长样本的批次化。虽然最近有学者通过因子分解和条件计算技巧重大的提升了计算效率，同时提升了模型的表现。但是序列计算的基本限制仍然存在。

注意力机制已经变成了序列建模和各种任务中的转导模型的必备成分，允许为依赖建模而不必考虑输入和输出序列中的距离远近。除了少数情况外，这种注意力机制都与循环神经网路结合使用。

本文我们提出了Transformer，一个移除循环网络、完全基于注意力机制来为输入和输出的全局依赖建模的模型。Transformer 允许更多的并行化，并且翻译质量可以达到最牛逼水平，只需要在8个P100 GPU上训练12个小时。

模型架构

Transformer模型抛弃了RNN和CNN，是一个完全利用自注意去计算输入和输出的编码器-解码器模型。并且它还可以并行计算，同时计算效率也很高。

模型整体架构如图1所示。

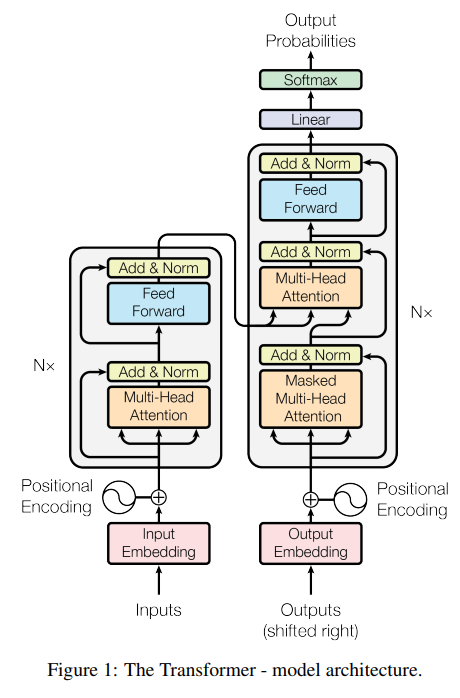
大部分有竞争力的神经网络序列转导模型都有一个编码器-解码器(Encoder-Decoder)结构。编码器映射一个用符号表示的输入序列$(x_1,\cdots ,x_n)$到一个连续的序列表示$z=(z_1,\cdots ,z_n)$。给定$z$，解码器生成符号的一个输出序列$(y_1,\cdots ,y_m)$，一次生成一个元素。在每个时间步，模型是自回归(auto-regressive)的，在生成下个输出时消耗上一次生成的符号作为附加的输入。

Transformer沿用该结构并在编码器和解码器中都使用叠加的自注意和基于位置的全连接网络，分别对应图1左半部和右半部。

我们先来看左边编码器部分。

编码器

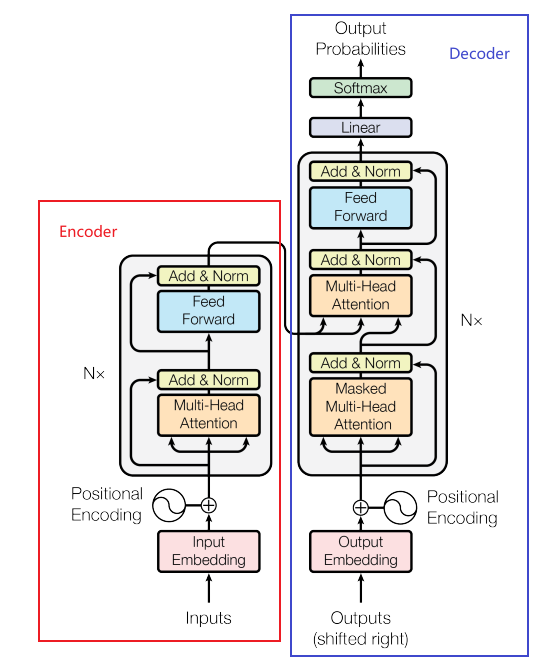
编码器是上图左边红色部分，解码器是上图右边蓝色部分。

编码器： 编码器是由$N=6$个相同的层(参数独立)堆叠而成的。

上图中的$N\times$是叠加$N$次的意思，原文中编码器是由6个相同的层堆叠而成的。如下图所示：

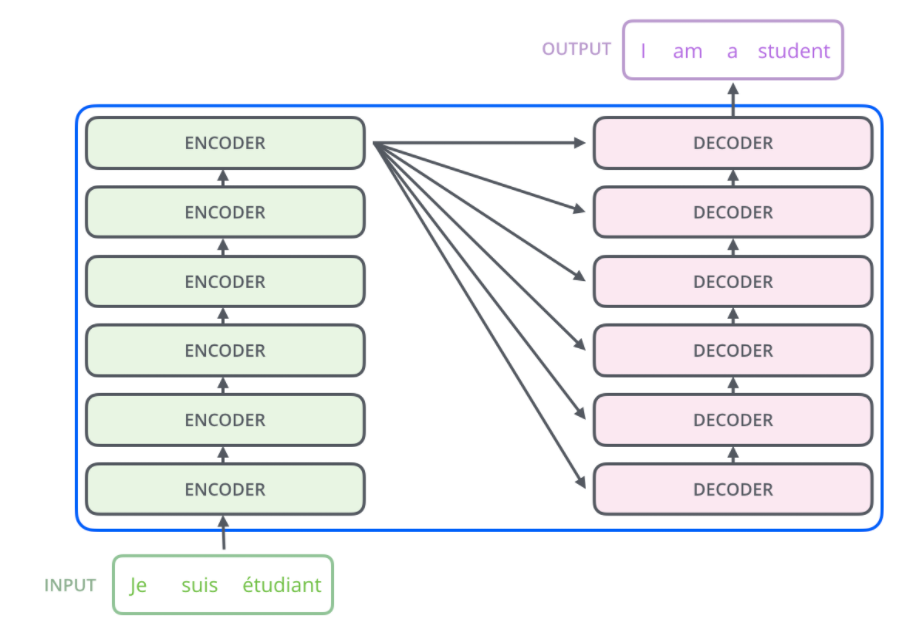
低层编码器的输出作为上一层编码器的输入。

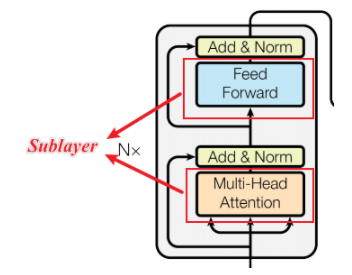
每层都有两个子层(sub-layer)，第一个子层是多头注意力层(Multi-Head Attention)，第二个是简单的基于位置的全连接前馈神经网络(positionwise fully connected feed-forward network)。

意思是每个编码器层都是由两个子层组成，第一个是论文中提出的多头注意力，这个比较重要，可以说是该篇论文的核心，理解了多头注意力整篇论文就理解的差不多了。后面会详细探讨。 经过多头注意力之后先进行残差连接，再做层归一化。

我们在两个子层周围先进行残差连接，然后进行层归一化(Layer Normalization)。这样，我们每个子层的输出是$LayerNorm(x+Sublayer(x))$，其中$Sublayer(x)$是子层自己实现的函数。为了利用残差连接，该模型中的所有子层和嵌入层，输出的维度都统一为$d_{model}=512$。

残差连接体现在上图的Add，层归一化就是上图的Norm。残差连接名字很唬人，其实原理非常简单，如下图：

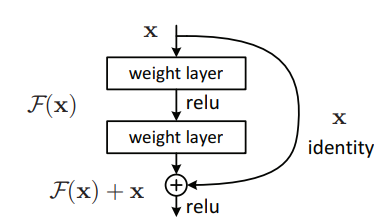
假设网络中某层输入$x$后的输出为$F(x)$，不管激活函数是什么，经过深层网络都可能导致梯度消失的情况。增加残差连接，相当于某层输入$x$后的输出为$F(x)+x$。最坏的情况相当于没有经过$F(x)$这一层，直接输入到高层，这样高层的表现至少能和低层一样好。

而层归一化针对每个输入的每个维度进行归一化操作。假设有$H$个维度，$x=(x_1,x_2,\cdots ,x_H)$，层归一化首先计算这$H$个维度的均值和方差，然后进行归一化得到$N(x)$，接着做一个缩放，类似批归一化。

$$\mu =\frac{1}{H}\sum _{i=1}^H{x}_i,\sigma =\sqrt{\frac{1}{H}\sum _{i=1}^H(x_i-\mu {)}^2},N(x)=\frac{x-\mu }{\sigma },h=g\odot N(x)+b\text{\hspace{1em}(1)}$$
其中$h$就是LN层的输出，$\odot$是点乘操作，$\mu$和$\sigma$是输入各个维度的均值和方差，$g$和$b$是两个可学习的参数，和$h$的维度相同。

Transformer中输入的维度$H=512$。

下面我们通过Pytorch实现上面编码器中介绍的部分，Pytorch版的Transformer依据的是另一个神作²，也是一篇论文，里面完整的实现了Transformer。本文的实现也是根据这篇论文来的，他们的代码写得非常优雅，从可重用性和抽象性来看，体现了非常高的技术，值得仔细研究学习。

import numpy as np
import torch
import torch.nn as nn
import math, copy, time
from torch.autograd import Variable
import matplotlib.pyplot as plt
import seaborn # # seaborn在可视化self-attention的时候用的到
seaborn.set_context(context="talk") 

# 防止jupyter plt.show崩溃
import os    
os.environ['KMP_DUPLICATE_LIB_OK']='True'
1
2
3
4
5
6
7
8
9
10
11
12

首先导入所有需要的包。然后我们定义一个克隆函数，Transformer中多处用到了叠加，叠加就可以通过克隆来实现。

def clones(module, N):
    '''
    生成N个相同的层
    '''
    # 每个进行的都是深克隆
    return nn.ModuleList([copy.deepcopy(module) for _ in range(N)])
1
2
3
4
5
6

ModuleList可以和Python普通列表一样进行索引，但是里面的模型会被合理的注册到网络中，这样里面模型的参数在梯度下降的时候进行更新。下面来看编码器的代码实现。

class Encoder(nn.Module):
    '''
    Encoder堆叠了N个相同的层，下层的输出当成上层的输入
    '''

    def __init__(self, layer, N):
        super(Encoder, self).__init__()

        self.layers = clones(layer, N)
        self.norm = LayerNorm(layer.size)

    def forward(self, x, mask):
        '''
        依次将输入和mask传递到每层
        :param x: [batch_size, input_len, emb_size]
        '''
        for layer in self.layers:
            # 下层的输出当成上层的输入
            x = layer(x, mask)
        # 最后进行层归一化
        return self.norm(x)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

编码器的输入是前文中提到的子层(sub-layer)，因此这里克隆了$N$份子层，由于用的是深克隆，虽然模型是一模一样的，但是每个模型学到的参数肯定是不同的。

注意这里输入mask的作用，编码器输入mask一般是在进行批处理时，由于每个句子的长度可能不等，因此对于过短的句子，需要填充<pad>字符，一般用$0$表示，而这里的mask就能标出哪些字符为填充字符，这样可以不需要进行计算，以提高效率。

注意这里用到的的层归一化，是对整个编码器的输出进行层归一化，即在编码器最终结果输出到解码器之前，做的层归一化。

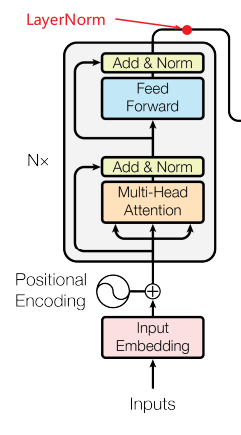
下面看一下层归一化LayerNorm的实现。

class LayerNorm(nn.Module):
    '''
    构建一个层归一化模块
    '''

    def __init__(self, features, eps=1e-6):
        super(LayerNorm, self).__init__()
        self.a_2 = nn.Parameter(torch.ones(features))
        self.b_2 = nn.Parameter(torch.zeros(features))
        self.eps = eps

    def forward(self, x):
        '''
        :param x: [batch_size, input_len, emb_size]
        '''
        # 计算最后一个维度的均值和方差
        mean = x.mean(-1, keepdim=True)
        std = x.std(-1, keepdim=True)
        return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

我们注意输入$x$的维度，最后一个维度就是嵌入层的大小，我们就是对该维度进行归一化。这里还有一点需要补充的就是，层归一化要学习的参数只有两个，上文公式$(1)$中的$g$和$h$，这里分别对应$a_2$和$b_2$。所以通过nn.Parameter去构造这两个参数，这样这两个参数会出现在该模型的parameters()方法中，并且可以注册到模型中。

由于层数较深，为了防止模型过拟合，故增加了Dropout。

我们应用dropout到每个子层的输出，在它被加到子层的输入(残差连接)和层归一化之前。此外，我们将dropout应用于编码器和解码器栈中的嵌入和位置编码的和。对于基本模型，我们使用dropout比率为$P_{drop}=0.1$。

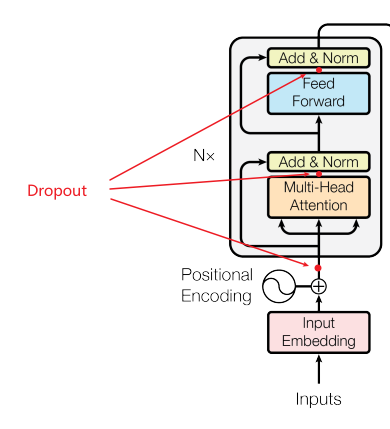
第一个应用Dropout的位置就是加入位置编码的词嵌入，后文会探讨。然后就是多头注意力层和全连接层的输出位置。

这里将上图中的Dropout、Add和Norm也设计成了一个模型(nn.Module)：

class SublayerConnection(nn.Module):
    '''
    残差连接然后接层归一化
    为了简化代码，先进行层归一化
    '''

    def __init__(self, size, dropout):
        '''
        :param size: 模型的维度，原文中统一为512
        :param dropout: Dropout的比率，原文中为0.1
        '''
        super(SublayerConnection, self).__init__()
        self.norm = LayerNorm(size)
        self.dropout = nn.Dropout(dropout)

    def forward(self, x, sublayer):
        '''
        应用残差连接到任何同样大小的子层
        '''
        return x + self.dropout(sublayer(self.norm(x)))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

这样，我们个子层的输出是$LayerNorm(x+Sublayer(x))$，其中$Sublayer(x)$是一个子层自己实现的函数。我们对每个子层的输出应用Dropout ，在其添加到(高层)子层输入并进行层归一化之前。

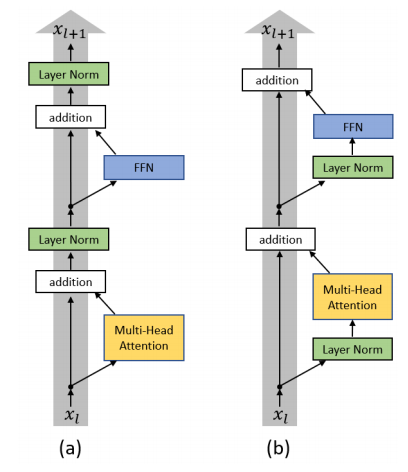
注意这里代码实现和原文中说的有点不同，主要是层归一化的位置，原文如上图$(a)$所示，叫Post-LN；这里的实现其实是上图$(b)$所示，叫做 Pre-LN。有人³ 证明Pre-LN这种方式效果更好。

我们知道编码器叠加了$N$层(EncoderLayer)，每层有两个子层，第一个是多头注意力层，第二个是一个简单的基于位置的全连接神经网络。

每个子层接了一个上面实现的SublayerConnection。

class EncoderLayer(nn.Module):
    '''
    编码器是由self-attention和FFN(全连接层神经网络)组成，其中self-attention和FNN分别用SublayerConnection封装
    '''

    def __init__(self, size, self_attn, feed_forward, dropout):
        '''
        :param: size: 模型的大小
        :param: self_attn: 注意力层
        :param: feed_forward: 全连接层
        '''
        super(EncoderLayer, self).__init__()
        self.self_attn = self_attn
        self.feed_forward = feed_forward
        # 编码器层共有两个子层
        self.sublayer = clones(SublayerConnection(size, dropout), 2) 
        self.size = size

    def forward(self, x, mask):
        x = self.sublayer[0](x, lambda x: self.self_attn(x, x, x, mask))
        return self.sublayer[1](x, self.feed_forward)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

其中sublayer[0]就是第一个子层连接，其中封装了第一个子层，即多头注意力层，我们上面已经知道它会对立面的网络层的输出进行残差连接和Dropout等操作。这里的多头注意层通过lambda表达式调用了self.self_attn，因为注意力层有三个输入和一个mask。

然后输入到第二个子层连接，其中封装的是基于位置的全连接层。

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/羊村懒王/article/detail/652783