- 1Flink集群安装和部署_flink 集群安装部署
- 2jenkins自动化部署(node服务器)_jenkins配置node
- 3【包邮送书】你好!Python_你好!python 全彩印刷
- 4从gitee上拉取项目至本地、本地项目上传gitee_gitee拉取的项目不会加载本地仓库
- 52024年春国家开放大学《马克思主义基本原理概论-试卷C》大作业答案
- 6OpenStack云计算基础架构平台搭建(国基北盛):第一篇_openstack云平台搭建
- 7SystemVerilog学习(0)——目录与传送门_systemverilog目录
- 8苹果电脑打不开U盘 苹果电脑不显示u盘怎么回事 mac优惠代码2020_mac u盘显示
- 9用Python历时十多天完成的全国所有区县经纬度采集_沿路采集经纬度
- 10【Leetcode栈与队列 232. 用栈实现队列】C++ 「重要基础」
常见排序算法汇总_常见的排序算法
赞
踩
一、选择排序
选择排序是最简单直观的排序算法。它的原理是对未排好序的数据进行循环遍历,每一轮遍历找出最小的元素,将其放到已排好序的序列末尾。无论输入的数据状况如何,都需要进行N轮遍历,因此时间复杂度是固定的 O ( N 2 ) O(N^2) O(N2)。优点是只需要申请有限的几个变量,空间复杂度为 O ( 1 ) O(1) O(1)。
代码如下:
/** * 选择排序 * @param arr */ private static void selectionSort(int arr[]){ for (int i = 0; i < arr.length-1; i++) { for (int j = i+1; j < arr.length; j++) { if(arr[j] < arr[i]){ // 交换 int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
二、插入排序
插入排序的基本思想是将一个新的元素插入到已经排好序的序列中。类似于我们打扑克时不断摸牌插入手牌的过程。
它的排序过程如下:
遍历数组,假设当前到达第 K 个元素,此时前面 0~K-1 个元素是已经排好序的,因此只需要比较第 K 个元素和第 K-1 个元素,如果前者比后者小,则交换两个元素,继续向前遍历,直到找到前者比后者大的数。
代码如下:
/** * 插入排序 * @param arr */ private static void insertionSort(int arr[]){ for (int i = 0; i < arr.length; i++) { for (int j = i-1; j >=0 ; j--) { // 0~n 时,如果arr[n-1]>arr[n],则交换 if(arr[j]>arr[j+1]){ arr[j] = arr[j] ^ arr[j+1]; arr[j+1] = arr[j] ^ arr[j+1]; arr[j] = arr[j] ^ arr[j+1]; } else { break; } } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
插入排序的时间复杂度在输入数据有序时,时间复杂度是 O ( N ) O(N) O(N),但平均和最坏情况下仍然是 O ( N 2 ) O(N^2) O(N2)。它的空间复杂度同样为 O ( 1 ) O(1) O(1)。
三、冒泡排序
对序列中的元素两两进行排序,在一次次遍历过程中,较小的元素会像水中的气泡一样慢慢上浮。
代码如下:
/**
* 冒泡排序
* @param arr
*/
private static void bubbleSort(int arr[]){
for (int i = 0; i < arr.length; i++) {
for (int j = 0; j < arr.length-1-i; j++) {
if(arr[j] > arr[j+1]){
int temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
四、归并排序
归并排序是分治算法的一种典型应用。它的基本思想是将原本的序列拆分成一个个小的片段,先对小的片段进行排序,然后片段之间组合,再进行排序。实际上就是从局部有序到整体有序的过程。
下面通过一个具体的例子展示其具体过程:

代码如下:
/** * 归并排序 * @param arr 输入数据 * @param L 左指针 * @param R 右指针 */ private static void process(int arr[],int L,int R){ // base case if(L==R){ return; } // 求出中点(其实就是(L+R)/2,先减后加防止溢出) int mid = L+((R-L)>>1); // 对左侧排序 process(arr,L,mid); // 对右侧排序 process(arr,mid+1,R); // 合并两边的子数组 merge(arr,L,mid,R); } /** * 合并方法 */ private static void merge(int arr[],int L,int M,int R){ // 临时数组,用来存储排好序的一段数组元素,最后会拷贝回原数组 int temp[] = new int[R-L+1]; // 临时数组的指针 int i = 0; // 左侧指针 int p1 = L; // 右侧指针 int p2 = M+1; // 左右两个指针所指元素进行比较,小的元素存入temp,它的指针向后移动 while(p1<=M && p2<=R){ temp[i++] = arr[p1]>arr[p2] ? arr[p2++]:arr[p1++]; } // 当其中一个指针已经走完,说明另一半数组剩余的元素都比当前元素大 // 所以将剩余的元素直接拷贝到临时数组 while(p1<=M){ temp[i++] = arr[p1++]; } while(p2<=R){ temp[i++] = arr[p2++]; } // 最后再将临时数组拷贝回原数组 for (int j = 0; j < temp.length; j++) { arr[L+j] = temp[j]; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
根据Master公式 T ( N ) = a ∗ T ( N / b ) + O ( N d ) T(N) = a*T(N/b) + O(N^d) T(N)=a∗T(N/b)+O(Nd)可以计算出归并排序的时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN)。
五、快速排序
快速排序也是分治算法的典型应用。我们可以通过一个例题来引出快速排序的基本思想:
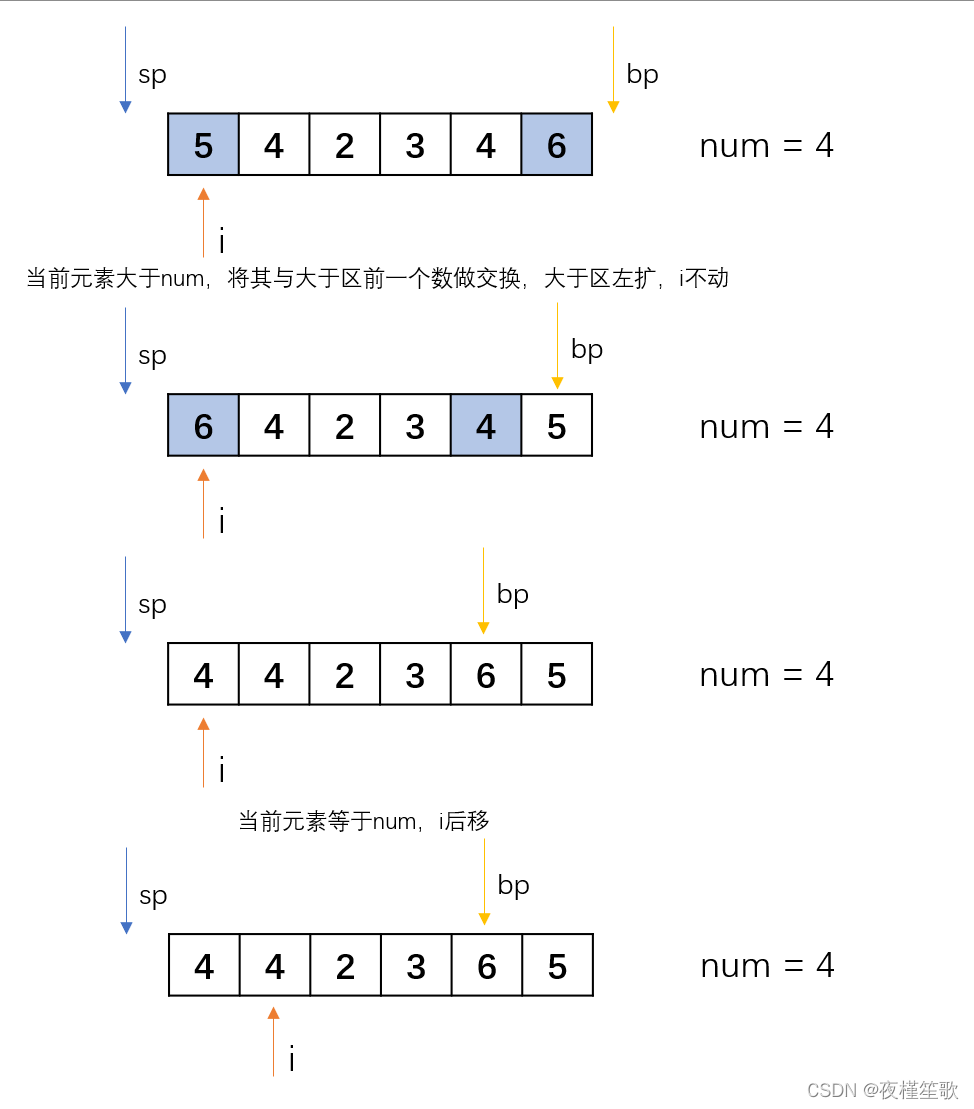
给定一个数组,和一个数num,要求将数组划分为左侧小于num,中间等于num和右侧大于num。
要求时间复杂度为O(N),空间复杂度为O(1)。
- 1
- 2
由于要求时间复杂度为 O ( N ) O(N) O(N),所以需要在有限次遍历中完成数组的划分。可以考虑维护两个指针,将数组划分为大于区、等于区和小于区。在遍历的过程中,两个指针的移动代表着大于区和小于区的边界的变化。通过这两个指针我们就可以了解当前已经排好序的元素有哪些,还没有排好序的元素有哪些。
下面通过一个例子展示其具体过程:

代码如下:
/** * 荷兰国旗问题 * @param arr 原数组 * @param num 基准值 */ private static void partition(int arr[],int num){ int i = 0; // 小于区指针 int smallPoint = -1; // 大于区指针 int bigPoint = arr.length; while(i<bigPoint){ // 小于时,当前元素与小于区下一个元素交换,小于区右扩 if(arr[i] < num){ int a = arr[smallPoint + 1]; arr[smallPoint + 1] = arr[i]; arr[i] = a; i++; smallPoint++; }else if(arr[i] == num){ // 等于时,只动指针 i++; }else{ // 大于时,大于区前一个元素与当前元素互换,大于区左扩 int a = arr[bigPoint - 1]; arr[bigPoint - 1] = arr[i]; arr[i] = a; bigPoint--; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
通过上面的例题我们可以发现,经过一轮partition处理,序列中等于区的元素已经被排好了位置,即前面的元素都小于等于区的元素,后面的元素都大于等于区的元素。那么如果对大于区和小于区分别进行上述处理,并依次递归下去,到最后我们不就能得到一串有序的序列了?其实这就是快速排序的基本思想。

快速排序采用了与归并排序类似的递归策略,因此时间复杂度也可以由Master公式得出为
O
(
N
l
o
g
N
)
O(NlogN)
O(NlogN),同时,快速排序在常数项上的时间复杂度要小很多,因此在一般情况下,快排的时间复杂度要优于归并排序。
但上述版本的快速排序存在一个问题,当面对本身顺序性较强的序列时,每次选择固定位置的基准数就会造成partition时只有大于区和等于区或只有小于区和等于区的情况:

相当于每轮遍历只排好了一个元素,所以此时时间复杂度为
O
(
N
2
)
O(N^2)
O(N2)。
为了优化最差情况下快排的性能,我们可以将“每次选择固定位置元素作为基准数”改为“每次选择随机位置的元素作为基准数”,这样虽然在每轮partition过程中的时间复杂度是不确定的,但总体上时间复杂度的期望值就是
O
(
N
l
o
g
N
)
O(NlogN)
O(NlogN)。
代码如下:
/** * 快速排序 * * @param arr 待排序数组 * @param L 左边界 * @param R 右边界 */ private static void process(int arr[], int L, int R) { if (L >= R) { return; } // 随机位置的元素与最后一位元素交换 swap(arr, (int) (L + Math.random() * (R - L + 1)), R); // 对当前序列进行划分 int a[] = partition(arr, L, R); // 对大于区和小于区进行排序 process(arr, L, a[0]); process(arr, a[1], R); } /** * 交换 */ private static void swap(int arr[], int index1, int index2) { int a = arr[index1]; arr[index1] = arr[index2]; arr[index2] = a; } /** * 划分 * * @param arr 要划分的数组 * @param L 左边界 * @param R 右边界 * @return 小于区最后一个元素和大于区第一个元素 */ private static int[] partition(int arr[], int L, int R) { // 小于区指针 int smallPoint = L - 1; // 大于区指针 int bigPoint = R; while (L < bigPoint) { // 当前数小于划分值,小于区下一个数与当前数交换,小于区右扩,L++ if (arr[L] < arr[R]) { swap(arr, ++smallPoint, L++); } else if (arr[L] > arr[R]) { // 当前数大于划分值,大于区上一个数与当前数交换,大于区左扩 swap(arr, --bigPoint, L); } else { // 当前数等于划分值,L++ L++; } } // 最后,将划分值与大于区第一位元素交换 swap(arr, R, bigPoint++); // 返回小于区末尾和大于区第一个元素 return new int[]{smallPoint, bigPoint}; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
六、堆排序
堆排序就是利用了堆这种数据结构进行排序的算法。主要使用以下两种堆:
大根堆:每个节点都比它的子节点大的完全二叉树。
小根堆:每个节点都比它的子节点小的完全二叉树。

那么堆是如何生成的呢?下面以大根堆为例进行讲解:
虽然堆是树形结构,但我们可以使用数组进行存储,以提高其读取的性能;同时,通过父子节点之间的位置关系计算,也可以以较小的时间复杂度实现新增和删除操作。堆结构主要有如下两种操作:
(1)上浮操作
当我们往堆中插入一个元素时,往往将其插入到最后一个位置,此时的堆有可能不再满足大根堆的特性,因此可以对新来的节点进行上浮操作,直到将堆调整回大根堆的状态。根据大根堆的特性——根节点比所有子节点大,我们在调整时只需要让新节点与自己的父节点进行比较,如果比父节点大则交换两个节点,直到遇到比自己大的父节点即停止。当前节点
i
i
i 的父节点位置也只需要通过计算获得:
(
i
−
1
)
/
2
(i-1)/2
(i−1)/2。


代码如下:
/**
* 上浮操作
* @param arr 堆数组
* @param index 要操作的元素下标
*/
private static void heapInsert(int arr[],int index){
// 当前节点比父节点大,交换两者位置
while(arr[index] > arr[(index-1)/2]){
swap(arr,index,(index-1)/2);
index = (index-1)/2;
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
(2)下沉操作
当我们要删除堆元素时,可以将堆最后一个元素补到堆顶(一般堆只会删除堆顶元素,删除其他元素没有意义),此时堆可能失去了大根堆的特性,因此我们要对新的堆顶节点进行下沉操作。只需要将其与自己较大的孩子进行比较,如果比它小,则交换位置,直到遇到比自己小的孩子节点。


代码如下:
/** * 下沉操作 * @param arr 堆数组 * @param index 要操作的元素下标 * @param heapSize 堆大小 */ private static void heapify(int arr[],int index,int heapSize){ // 先拿到左孩子节点 int left = index*2 + 1; while(left < heapSize){ // 找到最大的孩子节点 int largest = left+1 < heapSize && arr[left+1] > arr[left] ? left+1 : left; // 比较父节点与子节点 largest = arr[index] > arr[largest] ? index : largest; // 如果父节点更大,退出循环 if(largest == index){ break; } // 子节点大,则交换父节点与子节点 swap(arr,largest,index); // 继续向下寻找子节点 index = largest; left = index*2+1; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
掌握了上述两种堆的调整方法,堆排序就异常简单了,只需要将原序列一个一个插入(heapInsert)堆中,然后取出根节点,再对剩余的堆进行调整(heapify),循环往复,直到堆中的数据被取完。
代码如下:
/** * 堆排序 * @param arr 原数组 */ private static void heapSort(int arr[]){ // 转换成大根堆 for (int i = 0; i < arr.length; i++) { heapInsert(arr,i); } // 堆大小 int heapSize = arr.length; while(heapSize > 0){ // 交换首尾元素,并断开尾元素与堆的链接 swap(arr,0,--heapSize); // 对首元素进行下沉操作 heapify(arr,0,heapSize); } } /** * 交换 */ private static void swap(int arr[],int index1,int index2){ int a = arr[index1]; arr[index1] = arr[index2]; arr[index2] = a; }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
因为不管是heapify还是heapInsert操作,都只需要遍历堆的高度次,因此时间复杂度都是 O ( l o g N ) O(logN) O(logN)。在排序过程中需要对堆中的每个元素进行遍历,每遍历一个元素就会进行一次heapify操作,因此堆排序的时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN)。
七、 总结
排序的稳定性: 指进行一次排序后,原本相等的两个元素仍然保持着原本的顺序。因为在实际生产中,影响数据顺序的维度不止一个,经常遇到待排序属性相同,但不希望改变原输入顺序的情况,因此在某些情况下,排序算法是否具有稳定性也是纳入参考的标准之一。
稳定的排序算法:冒泡排序(相等时不进行交换)、插入排序(相等时不进行交换)、归并排序(相等时先挪动左指针)
不稳定的排序算法:选择排序、快速排序、堆排序
最后总结一下各个算法的时间、空间复杂度及稳定性:
| 时间复杂度 | 空间复杂度 | 稳定性 | |
|---|---|---|---|
| 选择排序 | O ( N 2 ) O(N^2) O(N2) | O ( 1 ) O(1) O(1) | 不稳定 |
| 冒泡排序 | O ( N 2 ) O(N^2) O(N2) | O ( 1 ) O(1) O(1) | 稳定 |
| 插入排序 | O ( N 2 ) O(N^2) O(N2) | O ( 1 ) O(1) O(1) | 稳定 |
| 归并排序 | O ( N l o g N ) O(NlogN) O(NlogN) | O ( N ) O(N) O(N) | 稳定 |
| 快速排序 | O ( N l o g N ) O(NlogN) O(NlogN) | O ( l o g N ) O(logN) O(logN) | 不稳定 |
| 堆排序 | O ( N l o g N ) O(NlogN) O(NlogN) | O ( 1 ) O(1) O(1) | 不稳定 |



