C语言——快速排序算法——堆排序_c语言堆排序算法

堆排序介绍

堆的概念

堆是一个完全二叉树（Complete Binary Tree），其中每个节点的值都大于等于（或小于等于）其子节点的值，这被称为堆的性质。具体来说，如果每个节点的值都大于等于其子节点的值，我们称之为 “最大堆”（Max Heap） ；如果每个节点的值都小于等于其子节点的值，我们称之为 “最小堆”（Min Heap）。

例如一个最大堆：

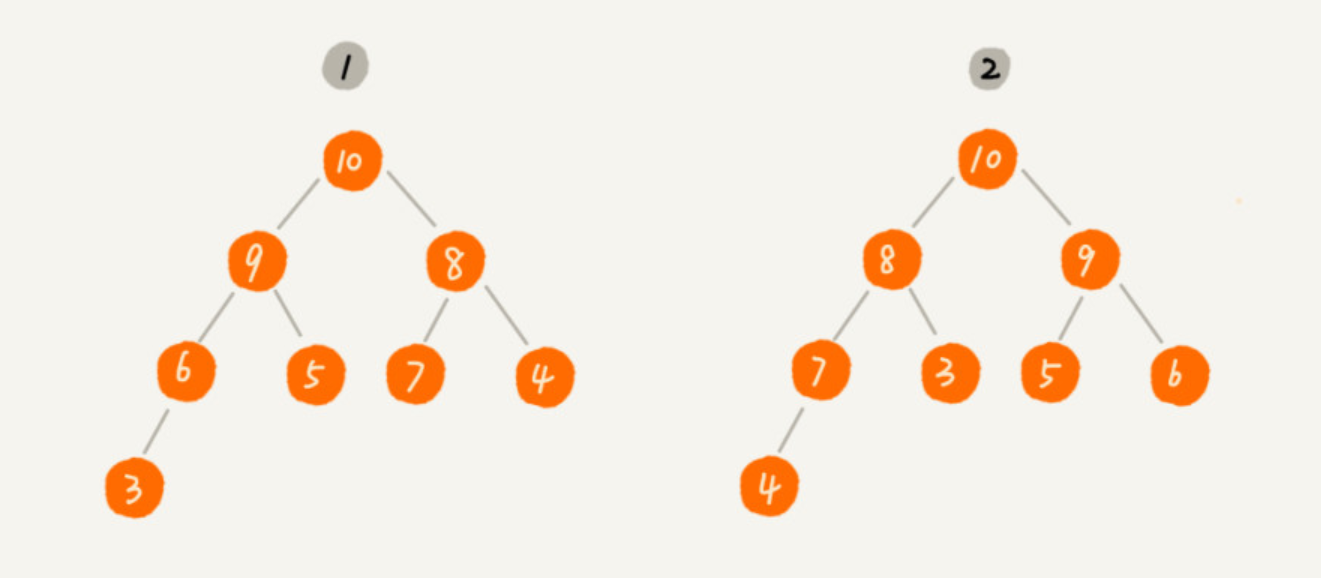
堆通常使用数组来实现，其中每个元素对应堆中的一个节点。通过索引关系可以方便地找到父节点、左孩子和右孩子。

堆的用处

1，实现优先队列：堆可以用来实现高效的优先队列。优先队列是一种数据结构，其中每个元素都关联有一个优先级，可以快速获取最高（或最低）优先级的元素。通过使用堆作为底层数据结构，可以实现在O(logn)的时间复杂度内插入和删除具有最高（或最低）优先级的元素，并在O(1)时间内访问堆顶元素。

2，排序算法：堆排序是一种基于堆的排序算法，它具有稳定的平均时间复杂度O(nlogn)，并且不需要额外的存储空间。堆排序利用了堆的性质，在建堆和调整堆的过程中完成排序操作。

3，图算法：在图算法中，堆被广泛应用于Dijkstra算法、Prim算法等最短路径和最小生成树的问题中。通过使用堆来维护节点的优先级，可以高效地选择下一个要处理的节点。

4，调度算法：在系统调度和任务调度的场景中，堆被用来管理和调度待执行的任务或进程。通过设置合适的优先级规则，并使用堆来维护任务的优先级顺序，可以实现高效的调度策略。

一个数组最大堆：

int arr[] = {12,10,5,9,8,3,2,4,1,7,6};
1

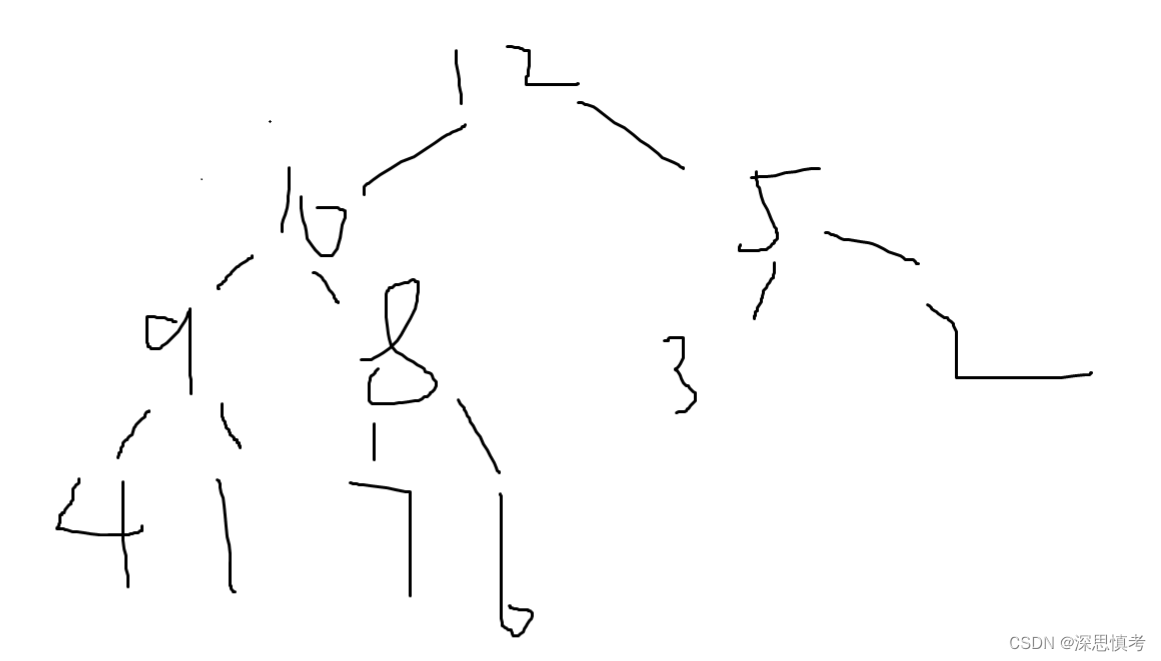
学习堆所需要的知识

1，基本输入与输出，分至于循环语句的掌握。

2,函数与指针的掌握，略微了解也可以。

3，对二叉树的理解，不懂也勉强可以试试学着看看。

向下调整算法

导言：

1，了解了堆的概念后的首个问题来了，如何建立一个堆呢？如果你遍历的话复杂度就高了，就算不上快速排序了，我们需要的是用尽量少的次数实现它，所以这里就要引入一个算法：向下调整算法。

2，有向下自然有向上，不过原理是差不多的，换了个顺序罢了，这里就不多赘述了，读者可以自己试试。

向下调整算法的介绍

1，概念：向下调整算法（也称为堆化算法或下沉操作）是在堆排序和优先队列等算法中使用的一种重要操作。它用于将一个节点下沉到合适的位置，以维持堆的性质。

ps:使用向下调整算法的要求它的根节点也就是第一个节点两边的字节点已经是最大堆或者最小堆了。

举个例子（最大堆）：

节点5就是需要调整的数字，我们需要将它下沉到合适的位置。

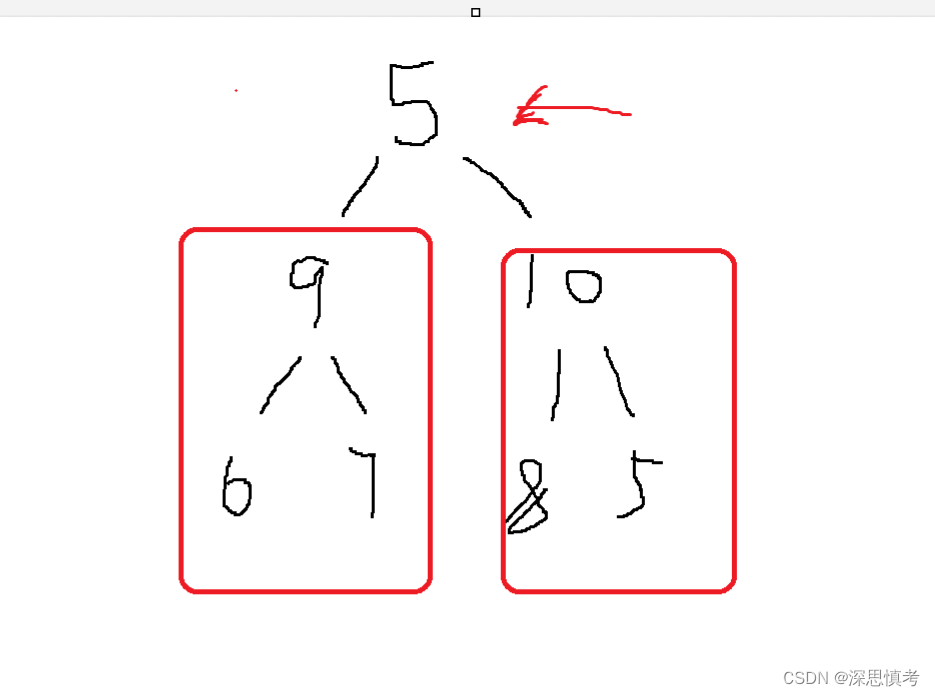
先提知识点

1，完全二叉树是数组的逻辑结构，便于我们理解的。每一层的节点数量是2^(h - 1)。

2，以此我们可以推出一个父节点的子节点的下标是 par * 2 + 1 和par * 2 + 2, par代表父节点的下标。

3，同理的，知道一个子节点我们也可以算出它的父节点的下标，公式如下： （kid - 1）/ 2 。

不信可以拿如下数组试试：

int arr[] = {1,2,3,4,5,6,7,8,9,10,11,12};
1

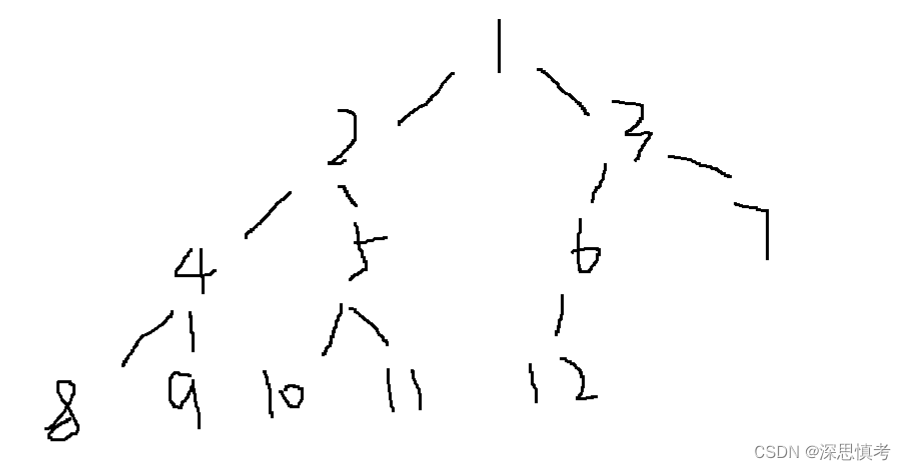
向下调整算法代码实现：

void swap(int* a, int* b)
{
	*a ^= *b;
	*b ^= *a;
	*a ^= *b;
}
//用位运算进行交换位置，不会这个也可以用别的算法
void Adjustdown(int* arr, int par, int end)
{
	//par为父节点，即要调整的节点。end是要调整的最后一个位置的索引。
	if (arr == NULL || par >= end)
	{
		return;  // 条件不对则直接返回停止函数
	}
	int kid = par * 2 + 1; // 父节点的左字节点
	while ( kid <= end && par <= end)
	{
		//进入循环不断向下调整，子节点和父节点都要小于等于结尾节点
		if (kid + 1 <= end && arr[kid] < arr[kid + 1])
		{
			kid++; // 比较两个子节点的大小，选出更大的在与父节点比较
		}
		if (arr[par] < arr[kid])
		{
			swap(&arr[par], &arr[kid]); // 如果父节点更小则交换位置下沉
			par = kid;
			kid = par * 2 + 1;    //更新父节点与子节点为下一个位置继续向下调整
		}
		else
		{
			break;   //如果不满足条件则不用调整直接结束
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35

如何建立堆

思考：

1，向下调整有了，但是有先提条件的，这样如何建立堆呢，我们建立一个数组刚开始的数据可不太可能根节点下面已经是堆了。

2，从上面不行我们可以从下面开始向上调整,我们也不用从最后一个数开始往上，我们从最后一个数的父节点开始调整，前面我们已经介绍过父节点的求发了，父节点：(end - 1) / 2开始调整，每次递减一个位置逐渐向上调整建立堆。

3，图解如下：

//随机建立一个数组
int arr[10] = {9,5,1,2,3,6,8,7,4,10};
1
2

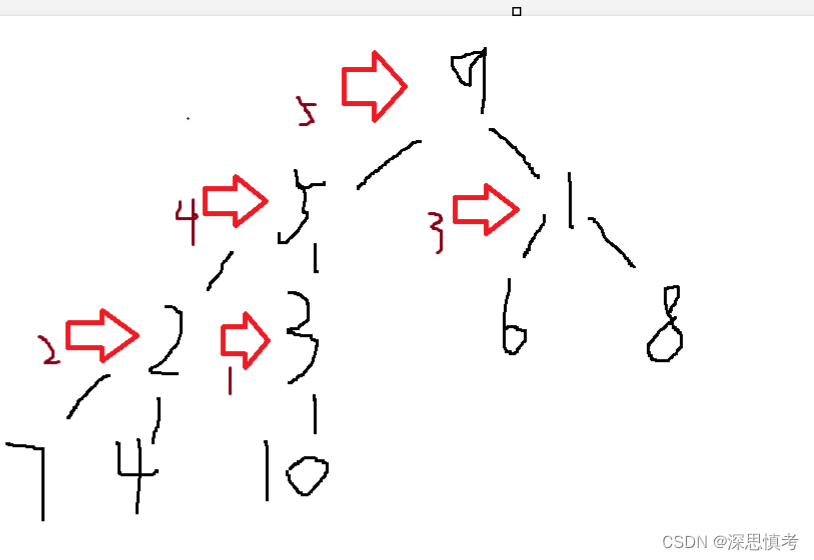
调整后：

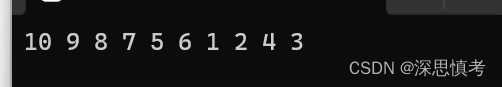
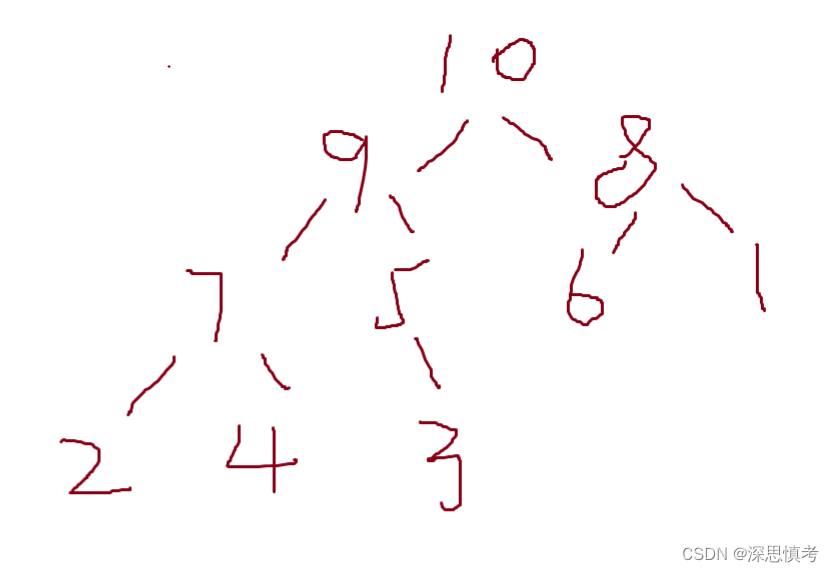
建立堆的代码实现

void heap(int* arr, int par, int end)
{
	int tail = (end - par - 1) / 2; //尾节点的父节点
	if (tail <= par)
	{
		//防止数组太小比如只有一两个数
		Adjustdown(arr, par, end);
	}
	else
	{
		while (tail >= par)
		{
			//开始调整
			Adjustdown(arr, tail, end);
			tail--;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

使用堆进行堆排序

进行从小到大的排序

1，建立最大堆进行由小到大的排序，为什么不是最小堆呢？

2，因为如果使用最小堆拿走第一个最小的下面的堆顺序就乱了要重新排序，复杂度提升了，而使用最大堆只需要把顶上最大的和结尾的数据交换一下，把结尾减一，在调整一次就可以继续了。

堆排序实现代码

void heapsort(int* arr, int par, int end)
{
	int tail = (end - par - 1) / 2;
	while (tail >= par)
	{
		Adjustdown(arr, tail, end);
		tail--;
	}
	 
	while (par < end)
	{
		//限制条件是父节点小于终止节点
		swap(&arr[par], &arr[end]); //交换首位，使最大数字移动到数组最后
		end--;   //结尾数字不需要在动，减一
		Adjustdown(arr, par, end);  //调整堆
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

总结

1，堆排序的效率是很高的，适合大数据的排序。平均复杂度为O（NlogN）。

2，这里只是简单的数组排序，读者可以试试使用结构体进行更复杂的插入，删除等操作。

如果有所收获就请点个小小的赞吧！