机器学习中为什么需要梯度下降?梯度下降算法缺点?_【机器学习-回归】梯度下降(SGD/BGD/MBGD)...

上一节讲完线性回归的模型思路与损失函数，我们的目的当然是求解参数

那么下面如何操作可以寻找到这个最值点呢？答：梯度下降。

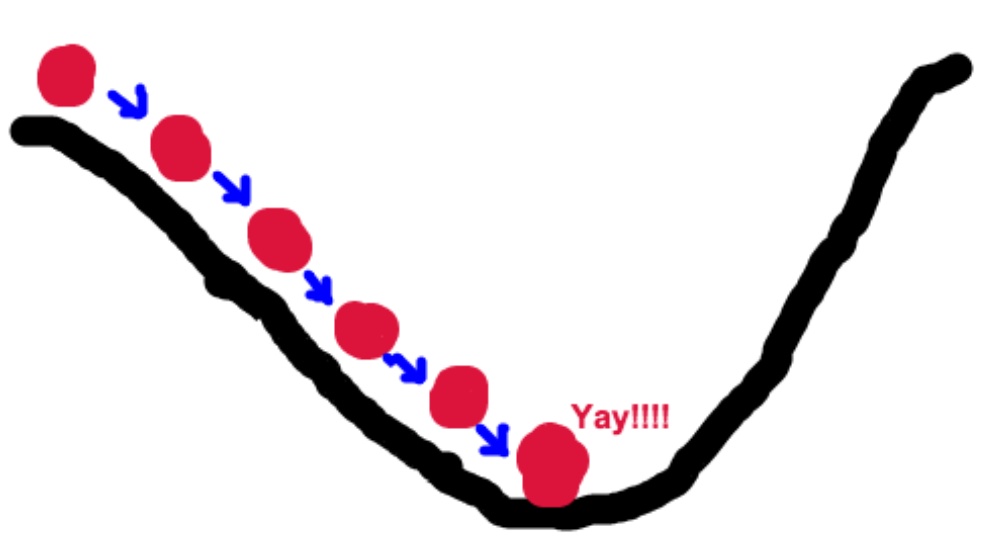
梯度下降法目的是寻找极值点，其本质可以类比为一个下山的过程。假设这样一个场景：一个人被困在山上，需要找到山谷。但由于视野等原因，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，朝着山的高度下降的地方走，然后不断调整方向。同理，如果我们的目标是上山，也就是爬到山顶，那么此时应该是朝着最陡峭的方向往上走。然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

鉴于此思想，可以得到由梯度下降的基本公式：

这里

结合前一篇文章线性回归(附链接)：

不愿露名的笨马：【机器学习-回归】线性回归​zhuanlan.zhihu.com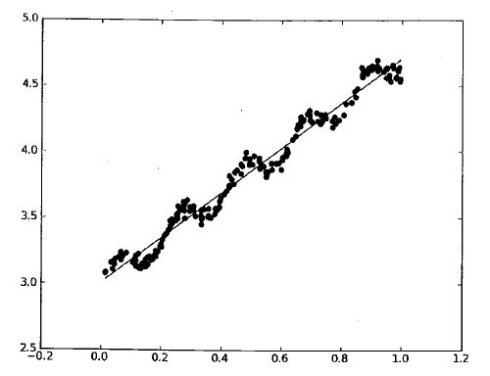

由于最终模型有形式：

且损失函数为：

则结合(1)式，可通过对

还有最后一个问题，根据怎样的样本确认梯度更新呢？这样就引出了以下三个概念：

1. 随机梯度下降 (Stochastic Gradient Descent,SGD):每次迭代使用一个样本对梯度更新。
2. 批量梯度下降(Batch Gradient Descent,BGD)：每次迭代时使用全部样本进行梯度更新。
3. 小批量梯度下降(Mini-Batch Gradient Descent,MBGD):每次迭代时使用若干样本进行梯度更新。

可以看出，MBGD可以看做SGD与BGD的折中办法，这里我们对比SGD与BGD的算法与优缺点。

随机梯度(SGD)

单样本损失函数：

对损失函数求偏导：

参数更新：

优势

1. 由于每次迭代所选取的样本少，在每轮迭代中，只随机优化某一条训练数据上的损失函数，使得每轮参数更新速度大大加快。

劣势

1. 同样由于每次迭代选取的样本少，梯度更新方向无法顾及到其余样本，因而准确性较低。
2. 同样的原因，容易收敛到局部最优解而非全局最优解(即使损失函数为凸)。
3. 难以并行。

批量梯度(BGD)

全体样本损失函数：

对损失函数求偏导：

参数更新：

优势

1. 每次迭代对全部样本计算，利用矩阵，可以并行计算。
2. 损失函数为凸时，可以得到全局最优解。

劣势

1. 训练速度慢。

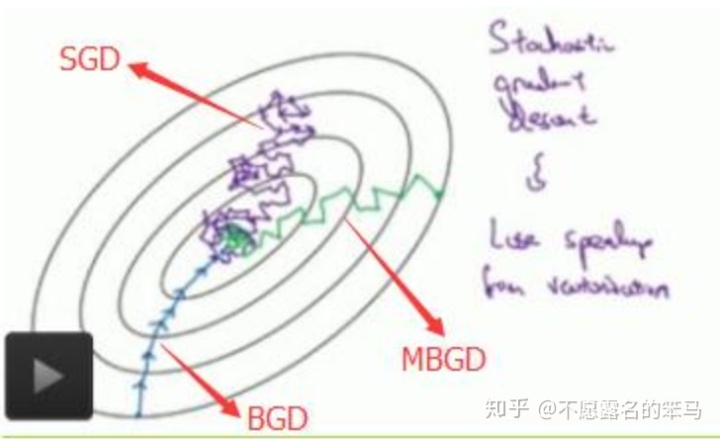
最后附一张SGD、BGD与MBGD之间的对照图。