【推荐收藏】三万字详解 TensorFlow 深度学习必备知识点（上）_学习 tensortflow需要用到哪些知识

各位同学大家好，想要学好深度学习，要么会 Pytorch，要么会 TensorFlow。

今天和大家分享一下 TensorFlow2.0 深度学习中的必备知识点。

解惑答疑

学了忘了、技术点不能吃透，可以加入技术交流，添加时最好的备注方式为：来源+兴趣方向，方便找到志同道合的朋友

方式①、添加微信号：mlc2060，备注：来自CSDN+加群
方式②、微信搜索公众号：机器学习社区，后台回复：加群

前向传播

1、数据获取

首先，我们导入需要用到的库文件和数据集。导入的x和y数据是数组类型，需要转换成tensor类型tf.convert_to_tensor()，再查看一下我们读入的数据有没有问题。

import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets # 数据集工具
import os  # 设置一下输出框打印的内容
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # '2'输出栏只打印error信息，其他乱七八糟的信息不打印

#（1）获取mnist数据集
(x,y),_ = datasets.mnist.load_data() 
#（2）转换成tensor类型，x数据类型一般为float32，y存放的是图片属于哪种具体类型，属于整型
x = tf.convert_to_tensor(x,dtype=tf.float32)
y = tf.convert_to_tensor(y,dtype=tf.int32)
#（3）查看数据内容
print('shape：',x.shape,y.shape,'\ndtype：',x.dtype,y.dtype)  #查看shape和数据类型
print('x的最小值：',tf.reduce_min(x),'\nx的最大值：',tf.reduce_max(x))  #查看x的数据范围
print('y的最小值：',tf.reduce_min(y),'\ny的最大值：',tf.reduce_max(y))  #查看y的数据范围
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

# 打印的结果如下
shape： (60000, 28, 28) (60000,) 
dtype： <dtype: 'float32'> <dtype: 'int32'>
x的最小值： tf.Tensor(0.0, shape=(), dtype=float32) 
x的最大值： tf.Tensor(255.0, shape=(), dtype=float32)
y的最小值： tf.Tensor(0, shape=(), dtype=int32) 
y的最大值： tf.Tensor(9, shape=(), dtype=int32)
1
2
3
4
5
6
7

2、数据预处理

首先对x数据进行归一化处理，原来x的每个像素值在[0,255]之间，现在转变成**[0,1]之间。刚导入的y数据的shape是[6000]，一维，存放分类数，为了和最后的预测结果比较，对它one-hot编码**，shape变为[6000,10]。存放每张图属于每一个分类的概率。y.numpy()[0]表示第0张图像属于第5个分类的概率是1，属于其他分类的概率是0。再设置一个学习率lr，用于每次迭代完成后更新神经网络权重参数，初始学习率以 0.01 ~ 0.001 为宜。

#（4）预处理
x = x/255.  # 归一化处理，将x数据的范围从[0,255]变成[0,1]
y = tf.one_hot(y,depth=10) # y是分类数值，对它进行one-hot编码，shape变为[b,10]
y.numpy()[0]  # 查看编码后的y的数据
# array([0., 0., 0., 0., 0., 1., 0., 0., 0., 0.], dtype=float32)

lr = 1e-3 # 学习率，设置过大，会导致loss震荡，学习难以收敛；设置过小，那么训练的过程将大大增加
1
2
3
4
5
6
7

加载数据集tf.data.Dataset.from_tensor_slices()，**生成迭代器的 **iter()，返回迭代器的下一个项目next()

#（5）指定一个选取数据的batch，一次取128个数据
train_db = tf.data.Dataset.from_tensor_slices((x,y)).batch(128)
train_iter = iter(train_db) # 指定迭代器
sample = next(train_iter) # 存放的每一个batch
# sample[0]存放x数据，sample[1]存放y数据，每个sample有128组图片
print('batch:',sample[0].shape,sample[1].shape)
# 打印结果： batch: (128, 28, 28) (128, 10)
1
2
3
4
5
6
7

3、构建网络

输入特征x的shape为[128,28,28]，即输入层有28*28个神经元，自定义隐含层1有256个神经元，隐含层2有128个神经元，最终输出结果是固定的10个分类。

根据每一层神经元的个数来确定每个连接层的shape，使用随机的截断高斯分布来初始化各个权重参数，将定义的变量从tensor类型，转变为神经网络类型variable类型。

#（6）构建网络
# 输入层由输入多少个特征点决定，输出层根据有多少个分类决定
# 输入层shape[b,784]，输出层shape[b,10]
# 构建网络，自定义中间层的神经元个数
# [b,784] => [b,256] => [b,128] => [b,10]

# 第一个连接层的权重和偏置，都变成tf.Variable类型，这样tf.GradientTape才能记录梯度信息
w1 = tf.Variable(tf.random.truncated_normal([784,256], stddev=0.1)) # 截断正态分布，标准差调小一点防止梯度爆炸
b1 = tf.Variable(tf.zeros([256])) #维度为[dim_out]
# 第二个连接层的权重和偏置
w2 = tf.Variable(tf.random.truncated_normal([256,128], stddev=0.1)) # 截断正态分布，维度为[dim_in, dim_out]
b2 = tf.Variable(tf.zeros([128])) #维度为[dim_out]
# 第三个连接层的权重和偏置
w3 = tf.Variable(tf.random.truncated_normal([128,10], stddev=0.1)) # 截断正态分布，维度为[dim_in, dim_out]
b3 = tf.Variable(tf.zeros([10])) #维度为[dim_out]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

4、前向传播运算

每一次迭代从train_db中取出128个样本数据，由于取出的 x数据的shape是[128,28,28]，需要将它的形状转变成 [128,28*28] 才能传入输入层 tf.reshape()。h = x @ w + b**，本层的特征向量和权重做内积，再加上偏置，将计算结果放入激活函数tf.nn.relu()，得到下一层的输入特征向量。最终得到的输出结果out**中存放的是每张图片属于每个分类的概率。

#（7）前向传播运算
for i in range(10):  #对整个数据集迭代10次
    # 对数据集的所有batch迭代一次
    # x为输入的特征项，shape为[128,28,28]，y为分类结果，shape为[128,10]
    for step,(x,y) in enumerate(train_db): # 返回下标和对应的值
        # 这里的x的shape为[b,28*28]，从[b,w,h]变成[b,w*h]
        x = tf.reshape(x,[-1,28*28]) #对输入特征项的维度变换，-1会自动计算b
    
        with tf.GradientTape() as tape: # 自动求导计算梯度，只会跟踪tf.Variable类型数据
            # ==1== 从输入层到隐含层1的计算方法为：h1 = w1 @ x1 + b1   
            # [b,784] @ [784,256] + [b,256] = [b,256]
            h1 = x @ w1 + b1  # 相加时会自动广播，改变b的shape，自动进行tf.broadcast_to(b1,[x.shape[0],256])
            # 激活函数，relu函数
            h1 = tf.nn.relu(h1)
            # ==2== 从隐含层1到隐含层2，[b,256] @ [256,128] + [b,128] = [b,128]
            h2 = h1 @ w2 + b2
            h2 = tf.nn.relu(h2)
            # ==3== 从隐含层2到输出层，[b,128] @ [128,10] + [b,10] = [b,10]
            out = h2 @ w3 + b3 # shape为[b,10]
            
            #（8）计算误差，输出值out的shape为[b,10]，onehot编码后真实值y的shape为[b,10]
            # 计算均方差 mse = mean(sum((y-out)^2)
            loss_square = tf.square(y-out)  # shape为[b,10]
            loss = tf.reduce_mean(loss_square) # 得到一个标量
            
        # 梯度计算
        grads = tape.gradient(loss,[w1,b1,w2,b2,w3,b3])
        
        # 注意：下面的方法，运算返回值是tf.tensor类型，在下一次运算会出现错误
        # w1 = w1 - lr * grads[0] # grads[0]值梯度计算返回的w1，是grad的第0个元素

        # 权重更新，lr为学习率，梯度每次下降多少
        # 因此需要原地更新函数，保证更新后的数据类型不变tf.Variable
        w1.assign_sub(lr * grads[0])
        b1.assign_sub(lr * grads[1])    
        w2.assign_sub(lr * grads[2])  
        b2.assign_sub(lr * grads[3]) 
        w3.assign_sub(lr * grads[4])    
        b3.assign_sub(lr * grads[5]) 
        
        if step % 100 == 0: #每100次显示一次数据
            print(f"第{step+1}次迭代，loss为{np.float(loss)}") #loss是tensor变量
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

计算输出结果和真实结果之间的均方差作为模型损失。使用tf.GradientTape()中的梯度计算方法tape.gradient()，用于更新下一次迭代的权重参数。公式为w1 = w1 - lr * grads[n]，但由于该公式返回的是tensor类型的变量，而tf.GradientTape()梯度计算方法，只能跟踪计算tf.variable类型的数据。因此需要使用**assign_sub()**函数原地更新权重参数，不造成变量类型改变。

# 最后一次循环循环，loss的输出结果为：
第1次迭代，loss为0.08258605003356934
第101次迭代，loss为0.09005936980247498
第201次迭代，loss为0.0828738585114479
第301次迭代，loss为0.0822446346282959
第401次迭代，loss为0.08802710473537445
1
2
3
4
5
6

前向传播 2

生成数据集： tf.data.Dataset.from_tensor_slices(tensor变量)

创建一个数据集，其元素是给定张量的切片

生成迭代器： next(iter())

---

next() 返回迭代器的下一个项目，iter() 获取可迭代对象的迭代器

# 返回2项数据，图像x_test，目标y_test
db = tf.data.Dataset.from_tensor_slices((x_test,y_test))
# 迭代器得到的第0个元素是图像，第1个元素是目标
next(iter(db))[0].shape  # TensorShape([32, 32, 3])
next(iter(db))[1].shape  # TensorShape([])
1
2
3
4
5

重新洗牌： .shuffle(buffer_size)

---

将序列的所有元素随机排序，不打散x和y之间的相互对应关系。维持一个buffer_size大小的缓存，每次都会随机在这个缓存区抽取一定数量的数据

调用函数： .map(func)

---

将func函数作用于dataset中的每一个元素

def preprocess(x,y):
    x = tf.cast(x, dtype=tf.float32)/255
    y = tf.cast(y, dtype=tf.int32)
    y = tf.one_hot(y,depth=10)
    return(x,y)
# 对Dataset中的数据进行函数所指定的预处理操作
db2 = db.map(preprocess)
# 生成迭代器
res = next(iter(db2))
# 查看数据
print(res[0].shape,res[1])
1
2
3
4
5
6
7
8
9
10
11

生成对列： .batch(batch_size)

---

tensor队列生成器，作用是按照给定的tensor顺序，把batch_size个tensor推送到文件队列，作为训练一个batch的数据，等待tensor出队执行计算

#（5）.batch 一次读取读取n张图片
db3 = db2.batch(32) # 每次读取32张图片
res = next(iter(db3)) # 生成迭代器，每次取出32张
print(res[0].shape,res[1].shape) #res[0]代表图像数据，res[1]代表目标
# (32, 32, 32, 3) (32, 10)
1
2
3
4
5

重复迭代： .repeat(count)

将数据重复count次，相当于我们训练时的epoch

db = tf.data.Dataset.from_tensor_slices((x_test,y_test))
db = db.repeat(2) # 迭代两次
db = db.repeat() # 永远不会退出
1
2
3

实例展示

只需要对训练数据y进行one-hot编码，因为训练集的y要和网络输出结果求损失。网络输出层得到的是每张图片属于每个分类的概率，是一个二维tensor，因此训练集的y也需要是一个二维tensor，才能做比较。而在测试过程中。预测出的结果是一个值，该图片属于哪个，真实值y_test也是一个值，只需要比较两个值是不是相同即可，不需要one-hot编码。

#（1）加载数据集，(x,y)存放训练数据，(x_test,y_test)存放测试数据
(x,y),(x_test,y_test) = datasets.fashion_mnist.load_data()
# 查看数据集信息
print('x-min:',x.min(),' x-max:',x.max(),' x-mean',x.mean())
print('x-shape:',x.shape,'\ny-shape:',y.shape)
print('x_test-shape:',x_test.shape,'\ny_test-shape:',y_test.shape)
print('y[:4]:',y[:4])  # 查看前4个y值

#（2）定义预处理函数
y = tf.one_hot(y,depth=10)  # one-hot编码，转换成长度为10的向量，对应索引的值变为1

def processing(x,y):
    x = tf.cast(x,tf.float32)/255.0  # x数据改变数据类型，并归一化
    y = tf.cast(y,tf.int32)  # 对目标y改变数据类型
    return(x,y)

#（3）生成训练集的Dataset
ds = tf.data.Dataset.from_tensor_slices((x,y))
# 对训练数据预处理
ds = ds.map(processing)
# 重新洗牌，每次迭代读取100张图片
ds = ds.shuffle(1000).batch(100)

#（4）生成测试集的Dataset
ds_tes = tf.data.Dataset.from_tensor_slices((x_test,y_test))
# 测试数据预处理
ds_tes = ds_tes.map(processing)
# 洗牌、确定batch
ds_tes = ds_tes.shuffle(1000).batch(100)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

# 前向传播
import numpy as np
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets # 数据集工具
import os  # 设置一下输出框打印的内容
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # '2'输出栏只打印error信息，其他乱七八糟的信息不打印

#（1）获取mnist数据集
(x,y),(x_test,y_test) = datasets.mnist.load_data() 

#（2）转换成tensor类型，x数据类型一般为float32，y存放的是图片属于哪种具体类型，属于整型
x = tf.convert_to_tensor(x,dtype=tf.float32)/255.0
y = tf.convert_to_tensor(y,dtype=tf.int32)

x_test = tf.convert_to_tensor(x_test,dtype=tf.float32)/255.0
y_test = tf.convert_to_tensor(y_test,dtype=tf.int32)

#（3）查看数据内容
print('shape：',x.shape,y.shape,'\ndtype：',x.dtype,y.dtype)  #查看shape和数据类型
print('x的最小值：',tf.reduce_min(x),'\nx的最大值：',tf.reduce_max(x))  #查看x的数据范围
print('y的最小值：',tf.reduce_min(y),'\ny的最大值：',tf.reduce_max(y))  #查看y的数据范围

#（4）预处理
y = tf.one_hot(y,depth=10) # 对训练数据的目标集的数值编码，变为长度为10的向量，对应索引的值变为1
lr = 1e-3 # 指定学习率

#（5）指定一个选取数据的batch，一次取128个数据
train_db = tf.data.Dataset.from_tensor_slices((x,y)).batch(128)
test_db = tf.data.Dataset.from_tensor_slices((x_test,y_test)).batch(128)

#（6）构建网络
# 构建网络，自定义中间层的神经元个数
# [b,784] => [b,256] => [b,128] => [b,10]

# 第一个连接层的权重和偏置，都变成tf.Variable类型，这样tf.GradientTape才能记录梯度信息
w1 = tf.Variable(tf.random.truncated_normal([784,256], stddev=0.1)) # 截断正态分布，标准差调小一点防止梯度爆炸
b1 = tf.Variable(tf.zeros([256])) #维度为[dim_out]
# 第二个连接层的权重和偏置
w2 = tf.Variable(tf.random.truncated_normal([256,128], stddev=0.1)) # 截断正态分布，维度为[dim_in, dim_out]
b2 = tf.Variable(tf.zeros([128])) #维度为[dim_out]
# 第三个连接层的权重和偏置
w3 = tf.Variable(tf.random.truncated_normal([128,10], stddev=0.1)) # 截断正态分布，维度为[dim_in, dim_out]
b3 = tf.Variable(tf.zeros([10])) #维度为[dim_out]

#（7）前向传播运算
for i in range(50):  #对整个数据集迭代10次
    # 对数据集的所有batch迭代一次
    # x为输入的特征项，shape为[128,28,28]，y为分类结果，shape为[128]
    for step,(x,y) in enumerate(train_db): # 返回下标和对应的值
        # 这里的x的shape为[b,28*28]，从[b,w,h]变成[b,w*h]
        x = tf.reshape(x,[-1,28*28]) #对输入特征项的维度变换，-1会自动计算b
    
        with tf.GradientTape() as tape: # 自动求导计算梯度，只会跟踪tf.Variable类型数据
            # ==1== 从输入层到隐含层1的计算方法为：h1 = w1 @ x1 + b1   
            # [b,784] @ [784,256] + [b,256] = [b,256]
            h1 = x @ w1 + b1  # 相加时会自动广播，改变b的shape，自动进行tf.broadcast_to(b1,[x.shape[0],256])
            # 激活函数，relu函数
            h1 = tf.nn.relu(h1)
            # ==2== 从隐含层1到隐含层2，[b,256] @ [256,128] + [b,128] = [b,128]
            h2 = h1 @ w2 + b2
            h2 = tf.nn.relu(h2)
            # ==3== 从隐含层2到输出层，[b,128] @ [128,10] + [b,10] = [b,10]
            out = h2 @ w3 + b3 # shape为[b,10]
            
            #（8）计算误差，输出值out的shape为[b,10]，onehot编码后真实值y的shape为[b,10]
            # 计算均方差 mse = mean(sum((y-out)^2)
            loss_square = tf.square(y-out)  # shape为[b,10]
            loss = tf.reduce_mean(loss_square) # 得到一个标量
            
        # 梯度计算
        grads = tape.gradient(loss,[w1,b1,w2,b2,w3,b3])
        # 权重更新，lr为学习率，梯度每次下降多少
        
        # 注意：下面的方法，运算返回值是tf.tensor类型，在下一次运算会出现错误
        # w1 = w1 - lr * grads[0] # 返回的w1在grad的第0个元素
        
        # 因此需要原地更新函数，保证更新后的数据类型不变tf.Variable
        w1.assign_sub(lr * grads[0])
        b1.assign_sub(lr * grads[1])    
        w2.assign_sub(lr * grads[2])  
        b2.assign_sub(lr * grads[3]) 
        w3.assign_sub(lr * grads[4])    
        b3.assign_sub(lr * grads[5]) 
        
        if step % 100 == 0: #每100次显示一次数据
            print(f"第{step+1}次迭代，loss为{np.float(loss)}") #loss是tensor变量
            # loss为nan，出现梯度爆炸的情况，初始化权重的时候变小一点
    
    #（9）网络测试
    # total_correct统计预测对了的个数，total_num统计参与测试的个数
    total_correct, total_num = 0, 0
    # 对网络测试，test必须要使用当前阶段的权重w和偏置b，测试当前阶段的计算精度
    for step,(x,y) in enumerate(test_db):
        x = tf.reshape(x,[-1,28*28])
        # 对测试数据进行前向传播
        # 输入层[b,784] => [b,256] => [b,128] => 输出层[b,10]
        h1 = x @ w1 + b1 # 输入特征和第一层权重做内积，结果加上偏置
        h1 = tf.nn.relu(h1) # 计算后的结果放入激活函数中计算，得到下一层的输入
        # 隐含层1=>隐含层2
        h2 = tf.nn.relu(h1 @ w2 + b2)  # [b,256] => [b,128]
        # 隐含层2=>输出层
        out = h2 @ w3 + b3  # [b,128] => 输出层[b,10]
        
        #（10）输出概率计算
        # 计算概率，out：shape为[b,10]，属于实数；prob：shape为[b,10]，属于[0,1]之间
        # 使用softmax()函数，使实数out映射到[0,1]的范围
        prob = tf.nn.softmax(out,axis=1) # out是二维的，在第1个轴上映射，即把某张图片属于某个类的值变成概率
        # 概率最大的值所在的位置索引是预测结果，即属于第几个分类
        predict = tf.argmax(prob, axis=1,output_type=tf.int32) # 每张图片的概率最大值所在位置，shape[b,10]，10所在的维度
        # 测试集的y不需要转换成one-hot，真实值y是一个数值，predict也是一个数值，两两相比较
        correct = tf.equal(predict, y) # 比较，返回布尔类型，相同为True，不同为False
        correct = tf.cast(correct,dtype=tf.int32) # 将布尔类型转换为int32类型
        correct = tf.reduce_sum(correct) # 每次取出的batch中，有多少张图片是预测对的
        # 1代表预测对了，0代表预测错了
        total_correct += int(correct)  # 统计对的个数，correct是tensor类型
        total_num += x.shape[0]  # 统计一共有多少组参与测试，x.shape=[128,28*28]，x.shape[0]有128张图片
        
    # 数据集整体完成一次迭代后
    accuracy = total_correct / total_num # 计算每一轮循环的准确率
    print(f'accuracy={accuracy}')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121

迭代50轮，结果如下。

第50个循环
第1次迭代，loss为0.04710124433040619
第101次迭代，loss为0.05284833908081055
第201次迭代，loss为0.050228558480739594
第301次迭代，loss为0.052753616124391556
第401次迭代，loss为0.05572255700826645
accuracy=0.7847
1
2
3
4
5
6
7

全连接层、激活函数

分享一下tensorflow2.0深度学习中的相关操作。内容有：

• (1) 全连接层创建：tf.keras.Sequential()，tf.keras.layers.Dense()

• (2) 输出方式： tf.sigmoid()，tf.softmax()，tf.tanh()，tf.nn.relu()，tf.nn.leaky_relu()

1、全连接层

全连接层在整个网络卷积神经网络中起到特征提取器的作用。全连接层将学到的特征表示映射到样本的标记空间。

（1）在全连接层中创建一层：tf.keras.layers.Dense()

units： 正整数，输出空间的维数

activation=None： 激活函数，不指定则没有

use_bias=True： 布尔值，是否使用偏移向量

kernel_initializer=‘glorot_uniform’： 核权重矩阵的初始值设定项

bias_initializer=‘zeros’： 偏差向量的初始值设定项

kernel_regularizer=None： 正则化函数应用于核权矩阵

bias_regularizer=None： 应用于偏差向量的正则化函数

kernel_constraint=None： 对权重矩阵约束

bias_constraint=None： 对偏置向量约束

（2）堆层构建全连接层：tf.keras.Sequential([layer1,layer2,layer3])

通过组合层来构建模型，直接堆叠各个层

1.1 创建单个连接层

首先构造一个shape为[4,478]的随机正态分布，构造一个连接层tf.keras.layers.Dense()，输出512个特征，shape为[4,512]。将输入层放入连接层自动调用 build() 函数创建权重w和偏置b，将计算结果返回给out。

# 创建单个连接层
import tensorflow as tf
# 构建输入
x = tf.random.normal([4,478])
# 输入的shape不需要指定，可以自动的根据输入的特征生成对应的权值
net = tf.keras.layers.Dense(512)
# 输出结果
out = net(x)
out.shape  # 输出结果的shape[4,512]
net.kernel.shape # 权值W的形状，W的shape为[478,512]
net.bias.shape # 偏置b的形状，X的shape为[4,478]
# 调用net函数时，自动判断，如果当前没有创建w和b，自动调用build函数
1
2
3
4
5
6
7
8
9
10
11
12

1.2 创建多个连接层

使用tf.keras.Sequential()堆叠构建全连接层；使用tf.keras.layers.Dense()创建每一个全连接层；使用build()构建输入层。网络结构为[b,10]=>[b,16]=>[b,32]=>[b,8]；通过summary()查看整体网络架构。通过model.trainable_variables查看网络的所有的权重和偏置。

#（4）创建多个全连接层
# 将所有连接层组成一个列表放入
from tensorflow import keras
# 构建全连接层
model = keras.Sequential([
    keras.layers.Dense(16, activation='relu'), #w的shape为[10,16]，b的shape为[16]，共10*16+16=176个参数  
    keras.layers.Dense(32, activation='relu'), #w的shape为[16,32]，b的shape为[32]
    keras.layers.Dense(8)])  #w的shape为[32,8]，b的shape为[8]

model.build(input_shape=[None,10]) #输入层10个特征
model.summary()  # 查看网络结构
# 查看网络所有的权重w和偏置b
for p in model.trainable_variables:
    print(p.name,p.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14

整体网络构架如下： 对于第一层，w的shape为[10,16]，b的shape为[16]，共10*16+16=176个参数 ，下面几层的参数个数同理

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense (Dense)               (None, 16)                176       
                                                                 
 dense_1 (Dense)             (None, 32)                544       
                                                                 
 dense_2 (Dense)             (None, 8)                 264       
                                                                 
=================================================================
Total params: 984
Trainable params: 984
Non-trainable params: 0
_________________________________________________________________
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

---

2、输出映射方式

2.1 sigmoid函数

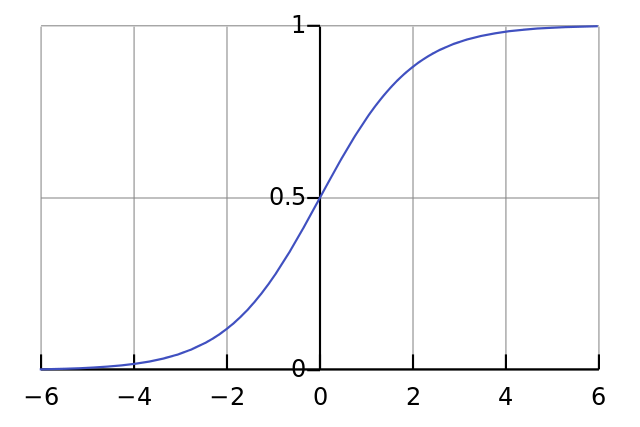
sigmoid函数：tf.sigmoid(tensor)

把输出结果的范围映射到(0,1)之间，计算公式：

sigmoid只能保证单个数值的范围在0-1之间

a = tf.linspace(-6,6,10) #-6到6的长度为10的向量
# sigmoid函数将其映射到0-1
tf.sigmoid(a)
# 输入数据：array([-6.        , -4.66666667, -3.33333333, -2.        , -0.66666667,0.66666667,  2.        ,  3.33333333,  4.66666667,  6.   
# 输出结果：array([0.00247262, 0.00931596, 0.0344452 , 0.11920292, 0.33924363,0.66075637, 0.88079708, 0.9655548 , 0.99068404, 0.99752738])
1
2
3
4
5

---

2.2 softmax函数

对于分类问题，需要每一个概率在0-1之间，且总的概率和为1。

softmax函数：tf.softmax(logits, axis)

logits：一个非空的Tensor。必须是下列类型之一：half， float32，float64。

axis：将在其上执行维度softmax。默认值为-1，表示最后一个维度。

公式为：

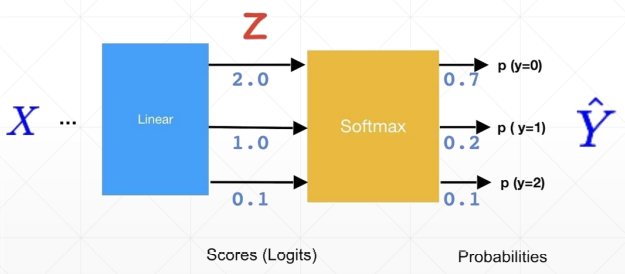
一般将没有加激活函数的称为Logits，加了softmax后称为Probabilities，经过softmax后，有把最大值放大的过程，相当于把强的变得更强，把弱的变得更弱。

logits = tf.random.uniform([1,10],minval=-2,maxval=2)
# 使用softmax
prob = tf.nn.softmax(logits,axis=1) #对整个列表的值求softmax
# 求和
tf.reduce_sum(prob,axis=1)

# logits：array([[-0.80400324,  1.1189251 ,  1.7390656 ,  0.8317995 , -1.1970901 ,-0.48806524, -1.1161256 , -0.35890388,  0.765254  , -1.8393846 ]],dtype=float32)>
# prob：array([[0.02841684, 0.19439851, 0.3614236 , 0.14588003, 0.01918051,0.03897498, 0.02079806, 0.0443486 , 0.13648833, 0.01009056]],dtype=float32)>
# sum：<tf.Tensor: shape=(1,), dtype=float32, numpy=array([1.], dtype=float32)>
1
2
3
4
5
6
7
8
9

---

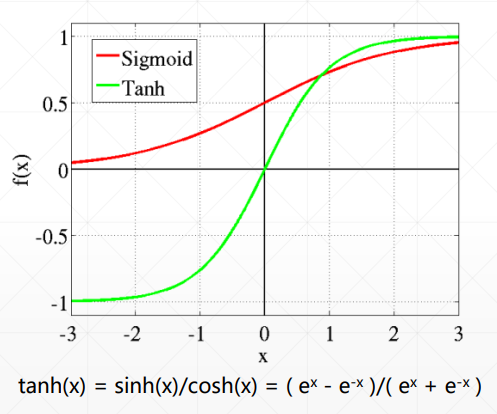
2.3 tanh函数

tanh是通过sigmoid函数放大平移得到，输出结果在(-1,1)之间

tanh函数： tf.tanh(tensor)

a = tf.linspace(-2, 2, 5)  # -2到2的长度为5的向量
# 结果映射到(-1,1)
tf.tanh(a)
# 输入：<tf.Tensor: shape=(5,), dtype=float64, numpy=array([-2., -1.,  0.,  1.,  2.])>
# 输出：<tf.Tensor: shape=(5,), dtype=float64, numpy=array([-0.96402758, -0.76159416,  0.        ,  0.76159416,  0.96402758])>
1
2
3
4
5

2.4 relu函数

将输入小于0的值都变成0，大于0的值保持不变。

relu激活函数：tf.nn.relu(features)

公式为：

# relu函数，x小于0，梯度0，x大于0梯度1
a = tf.linspace(-1,1,10) # -1到1，长度为10的向量
tf.nn.relu(a)

# 输入为：array([-1.        , -0.77777778, -0.55555556, -0.33333333, -0.11111111,        0.11111111,  0.33333333,  0.55555556,  0.77777778,  1.        ])>
# 输出为：array([0.        , 0.        , 0.        , 0.        , 0.        ,       0.11111111, 0.33333333, 0.55555556, 0.77777778, 1.        ])>
1
2
3
4
5
6

---

2.5 leaky_relu函数

---

非饱和激活函数： tf.nn.leaky_relu( features, alpha=0.2 )

features： tensor类型，表示预激活值，必须是下列类型之一：float16,float32,float64,int32,int64.

alpha： x <0时激活函数的斜率.

由于relu函数对于小于0的值，这个神经元的梯度永远都会是0，在实际操作中，如果数据很大，很可能网络中较多的神经元都死了。这时需要leaky_relu函数：

公式：y = max(0, x) + leak*min(0,x)

leak是一个很小的常数，这样保留了一些负轴的值，使得负轴的信息不会全部丢失

a = tf.linspace(-1,1,10)
# tf.nn.leaky_rulu() ，x小于0y也小于0但接近0
tf.nn.leaky_relu(a)

# 输入：array([-1.        , -0.77777778, -0.55555556, -0.33333333, -0.11111111,        0.11111111,  0.33333333,  0.55555556,  0.77777778,  1.        ])>
# 输出：array([-0.2       , -0.15555556, -0.11111111, -0.06666667, -0.02222222,        0.11111111,  0.33333333,  0.55555556,  0.77777778,  1.        ])>
1
2
3
4
5
6

梯度下降、损失函数

介绍一下TensorFlow2.0中的梯度下降、激活函数及其梯度、损失函数及其梯度。

• (1) 梯度计算：GradientTape()，tape.watch()，tape.gradient()

• (2) 损失函数及其梯度：MSE：tf.reduce_mean(tf.losses.MSE())，交叉熵：tf.losses.categorical_crossentropy()

---

1、梯度下降

---

1.1 自动求导函数：

GradientTape(persistent=False, watch_accessed_variables=True)

persistent： 布尔值，用来指定新创建的gradient tape是否是可持续性的。默认是False，意味着只能够调用一次GradientTape()函数。

watch_accessed_variables： 布尔值，表明GradientTape()函数是否会自动追踪任何能被训练的变量。默认是True。要是为False的话，意味着你需要手动去指定你想追踪的那些变量。

1.2 监视非Variable变量

tape.watch(tensor)

tape.watch()用于跟踪指定的tensor变量。由于GradientTape()默认只对tf.Variable类型的变量进行监控。如果需要监控的变量是tensor类型，则需要**tape.watch()**来监控，若是没有watch函数则梯度计算结果会是None。 如果指定跟踪的是tf.Variable类型，这一句就不用写了。

1.3 梯度计算

tape.gradient(target, sources, unconnected_gradients)

根据指定监视的变量来计算梯度

target： 求导的因变量

sources： 求导的自变量

unconnected_gradients： 无法求导时，返回的值，有两个可选值[none, zero]，默认none。

import tensorflow as tf
w = tf.constant(1.) # 创建全连接层
x = tf.constant(2.) # 创建输入特征
# 自动求导
with tf.GradientTape() as tape:
    tape.watch([w]) # 监视w
    y = x*w 
# 计算梯度，因变量y，自变量w
grad1 = tape.gradient(y,[w])
# 结果为： [<tf.Tensor: shape=(), dtype=float32, numpy=2.0>]
1
2
3
4
5
6
7
8
9
10

创建的权重w是tensor类型，需要tape.watch()函数，如果改成w = tf.Variable(tf.constant(1.))，将w变成Variable类型，就不需要tape.watch()函数来监视w。y=x*w，y对w求导结果为x，即为2.0。

2、损失函数及其梯度

2.1 均方误差MSE

计算公式：

y代表训练集的真实值，pred代表训练输出的预测结果，N通常指的是batch_size，也有时候是指特征属性个数。

MSE函数表示：

(1)tf.reduce_mean(tf.square(y - pred))

(2)tf.reduce_mean(tf.losses.MSE(y, pred))

一般而言，均方误差损失函数比较适用于****回归问题中，对于分类问题，特别是目标输出为One-hot向量的分类任务中，交叉熵损失函数要合适的多。

import tensorflow as tf
# 设有一组训练集的目标值
y = tf.constant([1,2,3,0,2]) 
y = tf.one_hot(y, depth=4) # 目标为四种分类
y = tf.cast(y,dtype=tf.float32)
# 设有一组模型输出的预测结果数据
out = tf.random.normal([5,4])
# 三种方法计算，预测结果out和真实值y之间的损失MSE
loss1 = tf.reduce_mean(tf.square(y-out))  # 1.2804947
loss2 = tf.square(tf.norm(y-out))/(5*4) # 1.2804947  #二范数方法
loss3 = tf.reduce_mean(tf.losses.MSE(y,out)) # 1.2804947
# 返回shape为[b]的tensor
1
2
3
4
5
6
7
8
9
10
11
12

2.2 MSE的梯度

使用tf.reduce_mean(tf.losses.MSE())计算真实值和预测结果的均方差，需要对真实值y进行one-hot编码tf.one_hot()，对应索引位置的值为1，分成三个类别depth=3。prob输出的也是图片属于三种分类的概率。使用**tape.gradient()**函数对跟踪的变量求梯度，grads[0]因变量为loss，自变量为w。

import tensorflow as tf
#（1）均方差MSE
x = tf.random.normal([2,4]) # 创建输入层，2张图片，各有4个特征
w = tf.random.normal([4,3]) #一层全连接层，输出每张图片属于3个分类的结果
b = tf.zeros([3]) # 三个偏置
y = tf.constant([2,0]) # 真实值，第一个样本属于2类别，第2个样本属于0类别
#梯度计算
with tf.GradientTape() as tape:
    tape.watch([w,b]) # 指定观测w和b，如果w和b时variable类型，就不需要watch了
    prob = tf.nn.softmax(x@w+b, axis=1) #将实数转为概率，得到属于3个节点的概率
    # 计算两个样本损失函数的均方差
    loss = tf.reduce_mean(tf.losses.MSE(tf.one_hot(y,depth=3),prob))
# 求梯度
grads = tape.gradient(loss,[w,b])
grads[0] # loss对w的梯度
grads[1] # loss对b的梯度
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

---

2.3 交叉熵

交叉熵（Cross Entropy）主要用于度量两个概率分布间的差异性信息，交叉熵越小，两者之间差异越小，当交叉熵等于0时达到最佳状态，也即是预测值与真实值完全吻合。

公式为：

式中，**p(x)**是真实分布的概率，**q(x)**是模型输出的预测概率。log的底数为2。

(1) 多分类问题交叉熵

tf.losses.categorical_crossentropy(y_true, y_pred, from_logits=False)

y_true： 真实值，需要one-hot编码

y_pred： 预测值，模型输出结果

from_logits： 为True时，会使用softmax函数将y_pred从实数转化为概率值，通常情况下用True结果更稳定

# 多分类
# 真实值和预测概率，预测结果均匀，交叉熵1.38很大
tf.losses.categorical_crossentropy([0,1,0,0],[0.25,0.25,0.25,0.25])
# 预测错了，交叉熵2.3
tf.losses.categorical_crossentropy([0,1,0,0],[0.1,0.1,0.7,0.1])
# 预测对了，交叉熵为0.35
tf.losses.categorical_crossentropy([0,1,0,0],[0.1,0.7,0.1,0.1])
1
2
3
4
5
6
7

(2) 二分类问题交叉熵

tf.losses.binary_crossentropy()

# 二分类
# 预测对了，0.1
tf.losses.binary_crossentropy([1,0],[0.9,0.1])
# 预测错了，2.3
tf.losses.categorical_crossentropy([1,0],[0.1,0.9])
1
2
3
4
5

(3) logits层直接计算交叉熵

模型的输出结果可能不是概率形式，通过softmax函数转换为概率形式，然后计算交叉熵，但有时候会出现数据不稳定的情况，即输出结果是NAN或者inf。

这种情况下可以通过logits层直接计算交叉熵，不过要给categorical_crossentropy()方法传递一个from_logits=True参数。

# 计算网络损失时，一定要加数值稳定处理参数from_logits=True，防止softmax和crossentropy之间的数值不稳定
import tensorflow as tf
x = tf.random.normal([1,784]) # 1张图片784个特征
w = tf.random.normal([784,2]) # 全连接层，分为2类
b = tf.zeros([2]) # 2个偏置

logits = x@w + b # 计算logits层

# 不推荐使用下面这种，会出现数值不稳定
# 输出结果映射到0-1，且概率和为1，(这一步由from_logits=True代替)
# prob = tf.math.softmax(logits,axis=1)
# tf.losses.categorical_crossentropy([[0,1]],prob)

# 计算交叉熵，一定要对y_true进行onehot编码
tf.losses.categorical_crossentropy([[0,1]],logits,from_logits=True)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

---

2.4 交叉熵的梯度

损失函数为计算交叉熵的平均值，一定要对训练集真实值y_true进行one-hot编码，分三类，tf.one_hot(y,depth=3)，跟踪权重w和偏置b，grads[0]为以loss为因变量，w为自变量计算梯度。grads[1]为以loss为因变量，b为自变量计算梯度

#（2）交叉熵cross entropy
# softmax，使logits数值最大的所在的所有作为预测结果的label
x = tf.random.normal([2,4]) # 输入层，2张图片，4个特征
w = tf.random.normal([4,3]) # 一层全连接层，输出三个分类
b = tf.zeros([3]) # 三个偏置
y = tf.constant([2,0]) # 第一个样本属于2类别，第2个样本属于0类别
# 梯度计算
with tf.GradientTape() as tape:
    tape.watch([w,b]) # 跟踪w和b的梯度
    logits = x @ w + b # 计算logits层
    # 计算损失，不要先softmax再使用交叉熵，会导致数据不稳定，categorical_crossentropy会自动执行softmax操作再计算损失
    loss = tf.reduce_mean(tf.losses.categorical_crossentropy(tf.one_hot(y,depth=3),logits,from_logits=True))
# 计算损失函数梯度
grads = tape.gradient(loss,[w,b])
grads[0] #shape为[4,3]
grads[1] #shape为[3]


# 结果为grads[0]：
array([[ 0.05101332,  0.08121025, -0.13222364],
       [ 0.1871956 , -0.02524163, -0.16195397],
       [-1.6817021 ,  0.17055441,  1.5111479 ],
       [-0.08085182,  0.06344394,  0.01740783]], dtype=float32)>
# grads[1]：
<tf.Tensor: shape=(3,), dtype=float32, numpy=array([-0.12239906,  0.08427953,  0.03811949], dtype=float32)>
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

案例

1、数据获取

使用系统内部的服装数据集构建神经网络。首先导入需要的库文件，x和y中保存训练集的图像和目标。x_test和y_test中保存测试集需要的图像和目标。(x, y)及(x_test, y_test)都是数组类型。

# keras层方式做前向传播，服装图片分类每一张图片28*28
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets,layers,optimizers,Sequential,metrics
# 导入数据集管理库，层级，优化器，全连接层容器，测试度量器
import os  # 设置一下输出框打印的内容
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # '2'输出栏只打印error信息，其他乱七八糟的信息不打印

#（1）导入数据集，数组类型
(x,y),(x_test,y_test) = datasets.fashion_mnist.load_data()
# 查看数据集信息
print(f'x.shape={x.shape}，y.shape={y.shape}') # 查看训练集xy的大小
print(f'x_test.shape={x_test.shape}，y_test.shape={y_test.shape}') #查看测试集的大小
print(f'y[:5]={y[:5]}') # 查看y的前5项数据
1
2
3
4
5
6
7
8
9
10
11
12
13
14

数据集信息如下，变量x中有60k张图片，每张图片的大小是28*28，变量y保存的是每张图片属于哪个分类。如，y[:5]=[9 0 0 3 0]，第一张图片属于第10个类别，第二张图片属于第0个类别。

x.shape=(60000, 28, 28)，y.shape=(60000,)
x_test.shape=(10000, 28, 28)，y_test.shape=(10000,)
y[:5]=[9 0 0 3 0]
1
2
3

为了我们能对这个数据集有个直观的认识，将图片信息绘制出来，展示前10张图像。

# 数据集展示
import matplotlib.pyplot as plt
import numpy as np
# 每个类别的名称
class_names = ['Tshirt','Trouser','Pullover','Dress','Coat','Sandal','Shirt','Sneaker','Bag','Ankle boot']
# 绘制图像
for i in range(0,10):
    plt.subplot(2,5,i+1) # 当前的图绘制在2行5列的第i+1个位置
    plt.imshow(x[i]) 
    plt.xlabel(class_names[y[i]]) #y[i]代表所属分类的标签值
    plt.xticks([])  # 不显示x和y轴坐标
    plt.yticks([])
1
2
3
4
5
6
7
8
9
10
11
12

2、数据加载

首先对训练集的目标值y进行one-hot编码，便于后续与预测结果计算损失。**从标量变成一个向量，索引对应的数值变成1。**如编码前y[0]=9，第一张图片对应的分类是第9类，编码后y[0]=[0., 0., 0., 0., 0., 0., 0., 0., 0., 1.]，第9个索引对应的值变成1，其他值都是0。

使用**tf.data.Dataset.from_tensor_slices()创建数据集，自动将输入的数组类型转变成tensor类型。使用.map()函数对数据集中的所有元素执行函数内容；使用.batch()函数指定每次迭代从数据集中取多少个数据，.shuffle()**打乱数据集，但不改变xy的对应关系，避免结果出现偶然性。

在对训练集预处理时，不需要对y_test数据进行one-hot编码，因为测试得到的预测结果是一个数值，和y_test比较，看是不是相同就行。

# 数据预处理函数，转变数据类型
def processing(x,y):
    x = tf.cast(x,tf.float32)/255.0  # x数据改变数据类型，并归一化
    y = tf.cast(y,tf.int32)  # 对目标y改变数据类型
    return(x,y)

#（2）数据加载
# 对训练集预处理
y = tf.one_hot(y,depth=10)  # one-hot编码，转换成长度为10的向量，对应索引的值变为1
ds_train = tf.data.Dataset.from_tensor_slices((x,y)) # 自动将x和y转换为tensor类型
ds_train = ds_train.map(processing).batch(128).shuffle(10000) # 设置每次采样大小，并打乱
# 对测试集预处理
ds_test = tf.data.Dataset.from_tensor_slices((x_test,y_test))
ds_test = ds_test.map(processing).batch(128) #一次测试完所有测试集样本呢，不需要打乱

# 生成迭代器，检测数据加载是否正确
sample = next(iter(ds_train)) # 运行一次取出一个batch，即128个数据
print('x_batch:',sample[0].shape,'y_batch:',sample[1].shape) # 查看一次取了多少个
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

构造一个迭代器来查看我们预处理后的数据是否正确，起检验作用。iter()函数生成一个迭代器，每执行一次next()函数，从ds_train中获取一组大小为batch的样本(x, y)，sample[0]保存x的数据，**sample[1]**保存y的数据。

# 输出结果
x.shape=(60000, 28, 28)，y.shape=(60000,)
x_test.shape=(10000, 28, 28)，y_test.shape=(10000,)
y[:5]=[9 0 0 3 0]
x_batch: (128, 28, 28) y_batch: (128, 10)
1
2
3
4
5

3、构建网络

使用堆层的方法构建全连接层 tf.keras.Sequential()，使用 tf.keras.layers.Dense()添加每一层，构建5层的全连接层，指定激活函数为relu函数，使网络的维度从[b,28*28]变换到最终的[b,10]，即输出10个分类的结果。使用**model.build()**函数指定输入层的输入特征大小，model.summary()查看整个网络的结构，指定优化器跟新权重和偏置optimizers.Adam()，学习率为0.001，即梯度下降速度。

#（3）构建网络
# ==1== 设置全连接层
# [b,784]=>[b,256]=>[b,128]=>[b,64]=>[b,32]=>[b,10]，中间层一般从大到小降维
model = Sequential([
    layers.Dense(256, activation=tf.nn.relu), #第一个连接层，输出256个特征
    layers.Dense(128, activation=tf.nn.relu), #第二个连接层
    layers.Dense(64, activation=tf.nn.relu), #第三个连接层
    layers.Dense(32, activation=tf.nn.relu), #第四个连接层
    layers.Dense(10), #最后一层不需要激活函数，输出10个分类
    ])

# ==2== 设置输入层维度
model.build(input_shape=[None, 28*28])
# ==3== 查看网络结构
model.summary()
# ==4== 优化器
# 完成权重更新 w = w - lr * grad
optimizer = optimizers.Adam(lr=1e-3) 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

网络结构如下，param代表每一层的参数个数，以最后一层为例，权重w的shape为[32,10]，偏置b的shape为[10]，参数个数为32*10+10=330

Model: "sequential"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 dense (Dense)               (None, 256)               200960    
                                                                 
 dense_1 (Dense)             (None, 128)               32896     
                                                                 
 dense_2 (Dense)             (None, 64)                8256      
                                                                 
 dense_3 (Dense)             (None, 32)                2080      
                                                                 
 dense_4 (Dense)             (None, 10)                330       
                                                                 
=================================================================
Total params: 244,522
Trainable params: 244,522
Non-trainable params: 0
_________________________________________________________________
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

4、网络训练

设置整个网络循环20次。for step,(x,y) in enumerate(ds_train)代表每次从训练集中取batch个样本用于训练，等把样本都取完了就完成一次循环。每次取出的x的shape为[128, 28, 28]，y的shape为[128, 10]。

使用model(x)会自动对输入的x完成权重和偏置计算，得到隐含层最后一层的输出结果logits。接下来计算损失函数，使用交叉熵更新权重偏置。梯度计算tape.gradient()，以loss2为因变量，权重和偏置为自变量计算梯度，**model.trainable_variables()**获取网络所有的权重和偏置。

zip(grads, model.trainable_variables) 将梯度和权重及偏置结合在一起。optimizer.apply_gradients()，使用优化器更新梯度，相当于计算w1 = w1 - lr * grads[0]，并原地更新权重偏置不改变数据类型，简化了w1.assign_sub(lr * grads[0])，不需要一个一个手敲计算更新梯度。

#（5）前向传播
for epoch in range(20): # 运行20次
    # 运行每一个batch
    for step,(x,y) in enumerate(ds_train):
        # ds_train中x的shape是[b,28,28]，由于输入层是[b,28*28]，需要类型转换
        x = tf.reshape(x, [-1, 28*28]) #-1会自动结算第0维
        # 梯度计算
        with tf.GradientTape() as tape:
            # 网络自动运行：[b,784]=>[b,10]
            logits = model(x) #得到最后一层的输出
            # 计算均方误差，真实值y(onehot编码后的)和输出结果之间
            loss1 = tf.reduce_mean(tf.losses.MSE(y, logits)) 
            # 计算交叉熵损失，真实值y(onehot编码后的)和输出概率(logits会自动进行softmax变成概率值)
            loss2 = tf.reduce_mean(tf.losses.categorical_crossentropy(y, logits, from_logits=True))
            
        # 梯度计算，第1个因变量，第2个自变量，model.trainable_variables获得所有的权重和偏置参数
        grads = tape.gradient(loss2, model.trainable_variables) 
        # 更新权重，zip将grads的元素和model.trainable_variables中的元素结合在一起
        optimizer.apply_gradients(zip(grads, model.trainable_variables)) # 完成任务：w1.assign_sub(lr * grads[0])
         
        # 每次运行完一个batch后打印结果
        if step % 100 == 0:
            print(f'epochs:{epoch}, step:{step}, loss_MSE:{loss1}, loss_CE:{loss2}')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

---

5、网络测试

网络测试是在20次的大循环内部的，使用总预测对了的个数除以总测试样本数来计算模型准确率。同样，每次迭代从测试集中取batch个样本，放入网络计算，得到输出层的结果logits，需要求预测结果概率最大值所在下标，知道了下标索引也就知道了每个测试样本属于第几个分类。

使用tf.nn.softmax()函数将输出结果映射到0-1之间，且概率和为1，再配合tf.argmax()就知道概率最大值所在的下标值。将预测值predict和真实值y比较，看是否相同，若相同就是预测对了。tf.equal()返回布尔类型，如果两个变量对应位置的值相同就返回True，再将布尔类型转换位数值类型即可求和tf.reduce_sum()。

#（6）网络测试--前向传播
    total_correct = 0 # 总预测对了的个数
    total_sum = 0 # 总统计的个数

    for (x,y) in ds_test: #返回测试集的x和y
        
        # 将x的shape从[b,28,28]=>[b,28*28]
        x = tf.reshape(x, [-1,28*28]) 
        # 计算输出层[b,10]
        logits = model(x)
        # 计算概率最大的值所在的索引        
        # 将logits转换为probility
        prob = tf.nn.softmax(logits, axis=1) # 在最后一个维度上转换概率，且概率和为1
        predict = tf.argmax(prob, axis=1) # 找到最大值所在位置，得到一个标量
        
        # y 是int32类型，shape为[128]
        # predict 是int64类型，shape为[128]
        predict = tf.cast(predict, dtype=tf.int32)

        # y是一个向量，每个元素代表属于第几类；predict也是一个向量，下标值指示属于第几类
        # 只要看两个变量的值是否相同
        correct = tf.equal(y, predict) #返回True和False
        # True和False变成1和0，统计1的个数，一共有多少个预测对了
        correct = tf.reduce_sum(tf.cast(correct, dtype=tf.int32))
        
        # 预测对了的个数，correct是tensor类型，变量numpy类型
        total_correct += int(correct) 
        total_sum += x.shape[0] #第0维度，每次测试有多少张图片 
    
    # 计算一次大循环之后的模型准确率
    acc = total_correct/total_sum
    print(f'acc: {acc}')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

---

6、结果展示

模型第1次循环，以及经过20次循环后的结果如下：

epochs: 0
loss_MSE: 16.709985733032227, loss_CE: 0.4360983967781067
acc: 0.839

epochs: 19
loss_MSE: 130.57691955566406, loss_CE: 0.27311569452285767
acc: 0.8878
1
2
3
4
5
6
7

完整代码如下

# keras层方式做前向传播，服装图片分类每一张图片28*28
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import datasets,layers,optimizers,Sequential,metrics
# 导入数据集管理库，层级，优化器，全连接层容器，测试度量器
import os  # 设置一下输出框打印的内容
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2' # '2'输出栏只打印error信息，其他乱七八糟的信息不打印

#（1）导入数据集，数组类型
(x,y),(x_test,y_test) = datasets.fashion_mnist.load_data()
# 查看数据集信息
print(f'x.shape={x.shape}，y.shape={y.shape}') # 查看训练集xy的大小
print(f'x_test.shape={x_test.shape}，y_test.shape={y_test.shape}') #查看测试集的大小
print(f'y[:5]={y[:5]}') # 查看y的前5项数据

#（2）数据预处理，转变为tenor类型
def processing(x,y):
    x = tf.cast(x,tf.float32)/255.0  # x数据改变数据类型，并归一化
    y = tf.cast(y,tf.int32)  # 对目标y改变数据类型
    return(x,y)

#（3）数据加载
# 对训练集预处理
y = tf.one_hot(y,depth=10)  # one-hot编码，转换成长度为10的向量，对应索引的值变为1
ds_train = tf.data.Dataset.from_tensor_slices((x,y)) # 自动将x和y转换为tensor类型
ds_train = ds_train.map(processing).batch(128).shuffle(10000) # 设置每次采样大小，并打乱
# 对测试集预处理
ds_test = tf.data.Dataset.from_tensor_slices((x_test,y_test))
ds_test = ds_test.map(processing).batch(128) #一次测试完所有测试集样本呢，不需要打乱
# 生成迭代器，检测数据加载是否正确
sample = next(iter(ds_train)) # 运行一次取出一个batch，即128个数据
print('x_batch:',sample[0].shape,'y_batch:',sample[1].shape) # 查看一次取了多少个

#（4）构建网络
# ==1== 设置全连接层
# [b,784]=>[b,256]=>[b,128]=>[b,64]=>[b,32]=>[b,10]，中间层一般从大到小降维
# 输入的维度会自动推算
model = Sequential([
    layers.Dense(256, activation=tf.nn.relu), #第一个连接层，输出256个特征
    layers.Dense(128, activation=tf.nn.relu), #第二个连接层
    layers.Dense(64, activation=tf.nn.relu), #第三个连接层
    layers.Dense(32, activation=tf.nn.relu), #第四个连接层
    layers.Dense(10), #最后一层不需要激活函数，输出10个分类
    ])

# ==2== 设置输入层维度
model.build(input_shape=[None, 28*28])

# ==3== 查看网络结构
model.summary()
# 330 = 权重参数32*10 + 偏置参数10

# ==4== 优化器
# 完成权重更新 w = w - lr * grad
optimizer = optimizers.Adam(lr=1e-3) 


#（5）模型训练--前向传播
for epoch in range(20): # 运行20次
    # 运行每一个batch
    for step,(x,y) in enumerate(ds_train):
        # ds_train中x的shape是[b,28,28]，由于输入层是[b,28*28]，需要类型转换
        x = tf.reshape(x, [-1, 28*28]) #-1会自动结算第0维
        # 梯度计算
        with tf.GradientTape() as tape:
            # 网络自动运行：[b,784]=>[b,10]
            logits = model(x) #得到最后一层的输出
            # 计算均方误差，真实值y(onehot编码后的)和输出结果之间
            loss1 = tf.reduce_mean(tf.losses.MSE(y, logits)) 
            # 计算交叉熵损失，真实值y(onehot编码后的)和输出概率(logits会自动进行softmax变成概率值)
            loss2 = tf.reduce_mean(tf.losses.categorical_crossentropy(y, logits, from_logits=True))
            
        # 梯度计算，第1个因变量，第2个自变量，model.trainable_variables获得所有的权重和偏置参数
        grads = tape.gradient(loss2, model.trainable_variables) 
        # 更新权重，zip将grads的元素和model.trainable_variables中的元素结合在一起
        optimizer.apply_gradients(zip(grads, model.trainable_variables)) # 完成任务：w1.assign_sub(lr * grads[0])
         
        # 每次运行完一个batch后打印结果
        # if step % 100 == 0:
        #     print(f'epochs:{epoch}, step:{step}, loss_MSE:{loss1}, loss_CE:{loss2}')
    # 一次循环完成的结果
    print(f'epochs: {epoch}, loss_MSE: {loss1}, loss_CE: {loss2}')
    
            
#（6）网络测试--前向传播
    total_correct = 0 # 总预测对了的个数
    total_sum = 0 # 总统计的个数

    for (x,y) in ds_test: #返回测试集的x和y
        
        # 将x的shape从[b,28,28]=>[b,28*28]
        x = tf.reshape(x, [-1,28*28]) 
        # 计算输出层[b,10]
        logits = model(x)
        # 计算概率最大的值所在的索引        
        # 将logits转换为probility
        prob = tf.nn.softmax(logits, axis=1) # 在最后一个维度上转换概率，且概率和为1
        predict = tf.argmax(prob, axis=1) # 找到最大值所在位置，得到一个标量
        
        # y 是int32类型，shape为[128]
        # predict 是int64类型，shape为[128]
        predict = tf.cast(predict, dtype=tf.int32)

        # y是一个向量，每个元素代表属于第几类；predict也是一个向量，下标值指示属于第几类
        # 只要看两个变量的值是否相同
        correct = tf.equal(y, predict) #返回True和False
        # True和False变成1和0，统计1的个数，一共有多少个预测对了
        correct = tf.reduce_sum(tf.cast(correct, dtype=tf.int32))
        
        # 预测对了的个数，correct是tensor类型，变量numpy类型
        total_correct += int(correct) 
        total_sum += x.shape[0] #第0维度，每次测试有多少张图片 
    
    # 计算一次大循环之后的模型准确率
    acc = total_correct/total_sum
    print(f'acc: {acc}')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116