机器学习-梯度下降算法原理及公式推导

     

目录

1.梯度下降直观理解解释

2.算法上的解释

3.常用的梯度下降法

4.梯度下降算法调优

5.其他优化算法对比

---

       在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降算法（Gradient Descent Algorithm）是最常采用的方法之一，也是众多机器学习算法中最常用的优化方法，几乎当前每一个先进的机器学习库或者深度学习库都会包括梯度下降算法的不同变种实现。

梯度就是导数

梯度下降法就是一种通过求目标函数的导数来寻找目标函数最小化的方法。

梯度下降目的是找到目标函数最小化时的取值所对应的自变量的值，目的是为了找自变量X。

 

       最优化问题在机器学习中有非常重要的地位，很多机器学习算法最后都归结为求解最优化问题。最优化问题是求解函数极值的问题，包括极大值和极小值。在各种最优化算法中，梯度下降法是最简单、最常见的一种，在深度学习的训练中被广为使用。

                                 

       如上图所示，当目标函数为g(x)时，求目标函数的最小值。一般首先求g(x)的导数，然后使导数等于0，那么目标函数的最小值为0，此时的自变量X取值为0。在这里我们可能会问：直接求函数的导数/梯度，然后令导数/梯度为0，解方程，问题不就解决了吗？事实上没这么简单，因为在机器学习中一般的目标函数方程可能很难解。比如下面的这个目标函数：

                         

我们分别对x和y求偏导数，并令它们为0，得到下面的方程组：

                            

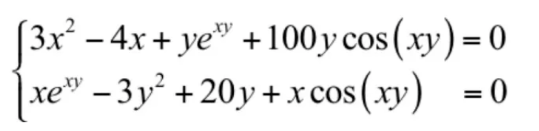
       这个方程非常难以求解，对于有指数函数，对数函数，三角函数的方程，我们称为超越方程，求解的难度并不比求极值本身小。精确的求解不太可能，因此只能求近似解，这称为数值计算。工程上实现时通常采用的是迭代法，它从一个初始点开始，反复使用某种规则从移动到下一个点，构造这样一个数列，直到收敛到梯度为0的点处，即梯度下降算法。

 

1.梯度下降直观理解解释

        梯度下降法的基本思想可以类比为一个下山的过程，如下图所示函数看似为一片山林，红色的是山林的高点，蓝色的为山林的低点，蓝色的颜色越深，地理位置越低，则图中有一个低点，一个最低点。

             

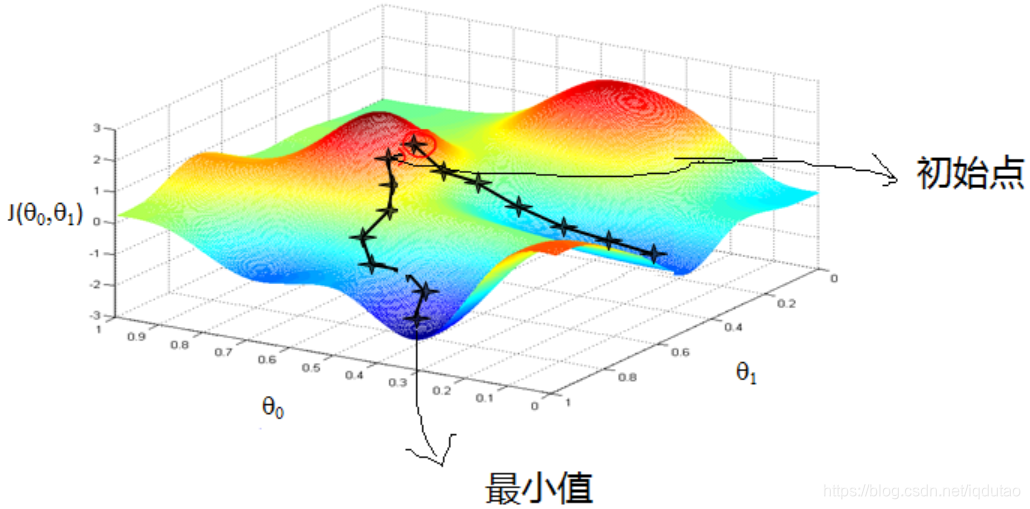
       假设这样一个场景：一个人被困在山上（图中红圈的位置），需要从山上下来(找到山的最低点，也就是山谷)，但此时山上的浓雾很大，导致可视度很低。因此，下山的路径就无法确定，他必须利用自己周围的信息去找到下山的路径。这个时候，他就可以利用梯度下降算法来帮助自己下山。具体来说就是，以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着山的高度下降的方向走，然后每走一段距离，都反复采用同一个方法，最后就能成功的抵达山谷。

                               

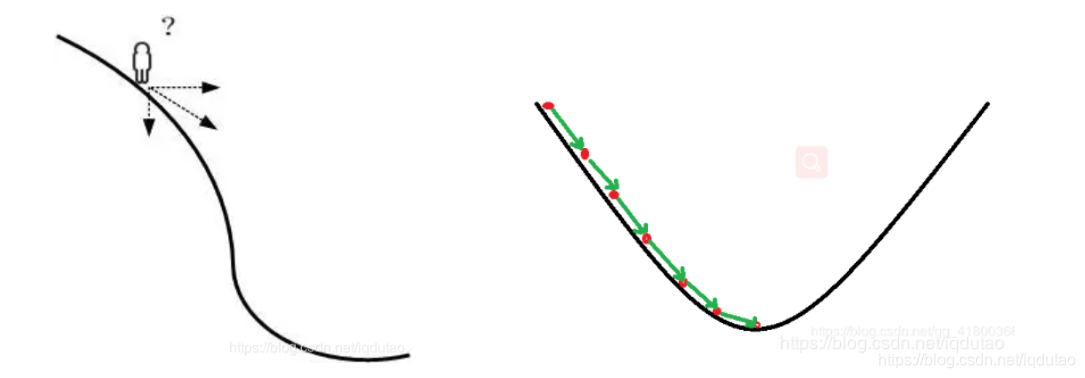
       假设这座山最陡峭的地方是无法通过肉眼立马观察出来的，而是需要一个复杂的工具来测量，同时，这个人此时正好拥有测量出最陡峭方向的工具。所以，此人每走一段距离，都需要一段时间来测量所在位置最陡峭的方向，这是比较耗时的。那么为了在太阳下山之前到达山底，就要尽可能的减少测量方向的次数。这是一个两难的选择，如果测量的频繁，可以保证下山的方向是绝对正确的，但又非常耗时，如果测量的过少，又有偏离轨道的风险。所以需要找到一个合适的测量方向的频率（多久测量一次），来确保下山的方向不错误，同时又不至于耗时太多，在算法中我们成为步长。

按照梯度下降算法的思想，它将按如下操作达到最低点：

第一步，明确自己现在所处的位置

第二步，找到相对于该位置而言下降最快的方向

第三步， 沿着第二步找到的方向走一小步，到达一个新的位置，此时的位置肯定比原来低

第四部， 回到第一步

第五步，终止于最低点

按照以上5步，最终达到最低点，这就是梯度下降的完整流程。当然你可能会说，上图不是有不同的路径吗？是的，因为上图并不是标准的凸函数，往往不能找到最小值，只能找到局部极小值。所以你可以用不同的初始位置进行梯度下降，来寻找更小的极小值点。

 

2.算法上的解释

                                   

       定义一个公式如上图所示，J是关于Θ的一个函数，我们在山林里当前所处的位置为Θ0点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是α，走完这个段步长，就到达了Θ1这个点。

                       

α在梯度下降算法中被称作为学习率或者步长，意味着我们可以通过α来控制每一步走的距离，以保证不要步子跨的太大，其实就是不要走太快，错过了最低点。同时也要保证不要走的太慢，导致太阳下山了，还没有走到山下。所以α的选择在梯度下降法中往往是很重要的！α不能太大也不能太小，太小的话，可能导致迟迟走不到最低点，太大的话，会导致错过最低点！

                        

我们假设有一个单变量的目标函数，函数的微分，初始化，起点为，我们通过观察就能发现最小值其实就是 (0，0)点。但是接下来，我们会从梯度下降算法开始一步步计算到这个最小值。

根据梯度下降的计算公式，我们开始进行梯度下降的迭代计算过程：

                       

如图，经过四次的运算，也就是走了四步，基本就抵达了函数的最低点，也就是山底，

                 

 

我们假设有多变量目标函数为，现在要通过梯度下降法计算这个函数的最小值。
我们假设初始的起点为：，初始的学习率为：，函数的梯度为：，进行多次迭代：

                 

我们发现，已经基本靠近函数的最小值点

                    

 

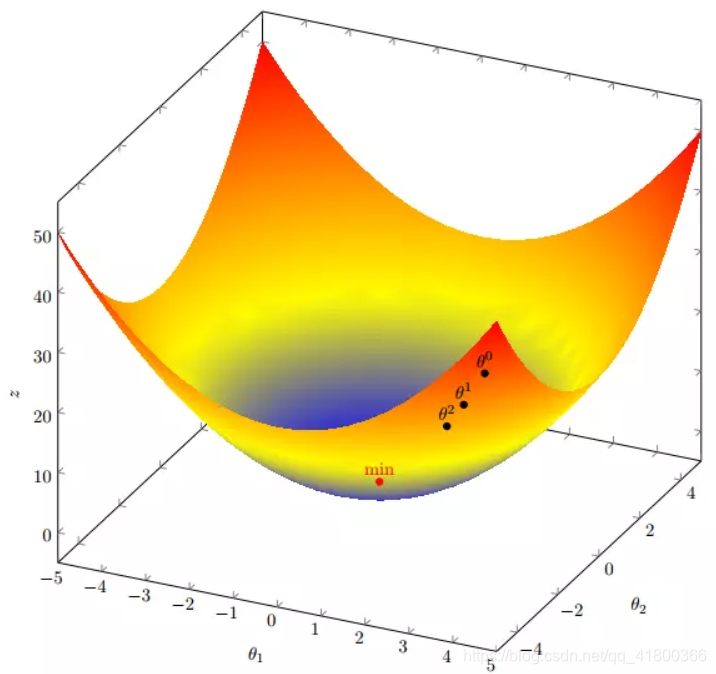
我们现在有一个线性回归的目标函数，为了方便，不带正则项，目标函数定义为：

                      

此公示中，各参数如下：

m 表示为数据集中样本的个数，表示有m个样本；

½是一个常量，这样是为了在求梯度的时候，二次方乘下来就和这里的½抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响；

y 是数据集中每个样本的实际值值；

h 是我们的预测函数，根据每一个输入x，根据θ计算得到预测的y值；

其中：

                      

其更新过程可写成：

                 

                   

其中，“:=”为赋值的含义；α为学习速率，又叫步长；α右边的是J(θ)对θ求的偏导（偏导就是对θ向量中的每个元素分别求导）。

这个公式的含义就是，先初始确定一个θ的值，然后用（1）式计算新的w值，反复迭代。我们不断更新参数θ的值，直到J(θ)取得最小值时，停止迭代。

具体的梯度下降流程：

第一步：先随便假设一组θ，可以全部取0

第二步循环迭代:

第一次迭代：

第二次迭代：

第x次迭代：......

第三步，满足要求，循环结束，得到θ

 

3.常用的梯度下降法

       梯度下降算法又通常称为批量梯度下降算法。批量梯度下降每次学习都使用整个训练集，因此这些计算是冗余的，因为每次都使用完全相同的样本集。但其优点在于每次更新都会朝着正确的方向进行，最后能够保证收敛于极值点(凸函数收敛于全局极值点，非凸函数可能会收敛于局部极值点)，但是其缺点在于每次学习时间过长，如果训练集很大以至于需要消耗大量的内存，并且全量梯度下降不能进行在线模型参数更新。它的具体思路是在更新每一参数时都使用所有的样本来进行更新，其数学形式如下：

(1) 对上述的能量函数求偏导：

                                             

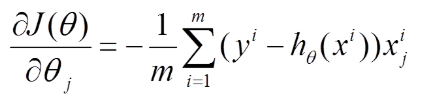
(2) 由于是最小化风险函数，所以按照每个参数θθ的梯度负方向来更新每个θ：

                                             

具体的伪代码形式为：

                                
从上面公式可以注意到，它得到的是一个全局最优解，但是每迭代一步，都要用到训练集所有的数据，所以在下图的梯度下降过程中可以看到，它是一个近乎直线的下降过程，直接前往最低点。

                              

 

随机梯度下降算法（Stochastic Gradient Descent）

       为了克服批量梯度下降的缺点，有人提出了随机梯度下降(Stochastic Gradient Descent)算法，即每次更新系数只随机抽取一个样本参与计算，因此既可以减少迭代次数，节省计算时间，又可以防止内存溢出，降低了计算开销。但是随机梯度下降也有一个缺点，每次更新可能并不会按照正确的方向进行，因此可以带来优化波动(扰动)，即参数更新频率太快，有可能出现目标函数值在最优值附近的震荡现象，并且高频率的参数更新导致了高方差。不过从另一个方面来看，随机梯度下降所带来的波动有个好处就是，对于类似盆地区域（即很多局部极小值点）那么这个波动的特点可能会使得优化的方向从当前的局部极小值点跳到另一个更好的局部极小值点，这样便可能对于非凸函数，最终收敛于一个较好的局部极值点，甚至全局极值点。

随机梯度下降虽然提高了计算效率，但是由于每次迭代只随机选择一个样本，因此随机性比较大，所以下降过程中非常曲折，如下图所示：

                            

它的具体思路是在更新参数时都随机抽泣一个样本来进行更新，其数学形式如下：

将上面的能量函数写为如下形式：

                                    

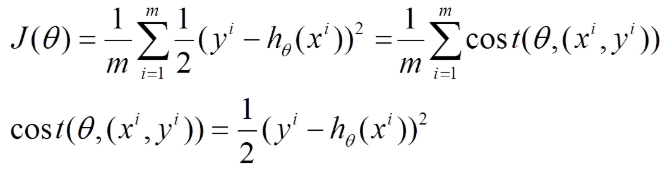
利用每个样本的损失函数对θθ求偏导得到对应的梯度，来更新θ：

                                          

具体的伪代码形式为：

                                       

       随机梯度下降是通过每个样本来迭代更新一次，如果样本量很大的情况（例如几十万），那么可能只用其中几万条或者几千条的样本，就已经将theta迭代到最优解了，对比上面的批量梯度下降，迭代一次需要用到十几万训练样本，一次迭代不可能最优，如果迭代10次的话就需要遍历训练样本10次。但是，SGD伴随的一个问题是噪音较BGD要多，使得SGD并不是每次迭代都向着整体最优化方向。

　   随机梯度下降法和批量梯度下降法是两个极端，一个采用所有数据来梯度下降，一个用一个样本来梯度下降，自然各自的优缺点都非常突出。对于训练速度来说，随机梯度下降法由于每次仅仅采用一个样本来迭代，训练速度很快，参数更新频率太快；而批量梯度下降法在样本量很大的时候，训练速度很慢。对于准确度来说，随机梯度下降法用于仅仅用一个样本决定梯度方向，导致解很有可能不是最优。对于收敛速度来说，由于随机梯度下降法一次迭代一个样本，导致迭代方向变化很大，不能很快的收敛到局部最优解。

 

小批量梯度下降(Mini-batch Gradient Descent)

       小批量梯度下降(Mini-batch Gradient Descent)是介于上述两种方法之间的优化方法，即在更新参数时，只使用一部分样本（一般256以下）来更新参数，这样既可以保证训练过程更稳定，又可以利用批量训练方法中的矩阵计算的优势。MBGD在每次更新参数时使用b个样本（b一般为10），其具体的伪代码形式为：

                                 

 

4.梯度下降算法调优

        尽管梯度下降算法效果非常好，而且广泛使用，但同一时候其也存在一些挑战与问题须要解决：选择一个合理的学习速率非常难，假设学习速率过小，则会导致收敛速度非常慢；假设学习速率过大，那么其会阻碍收敛，即在极值点附近会振荡。学习速率调整(又称学习速率调度，Learning rate schedules)试图在每次更新过程中，改变学习速率，如退火。一般使用某种事先设定的策略或者在每次迭代中衰减一个较小的阈值。不管哪种调整方法，都须要事先进行固定设置。这边便无法自适应每次学习的数据集特点。

        模型所有的參数每次更新都是使用同样的学习速率。假设数据特征是稀疏的或者每一个特征有着不同的取值统计特征与空间，那么便不能在每次更新中每一个參数使用同样的学习速率。那些非常少出现的特征应该使用一个相对较大的学习速率。对于非凸目标函数。easy陷入那些次优的局部极值点中，如在神经网路中。

在使用梯度下降时，需要进行调优，哪些地方需要调优呢？

（1）算法的步长选择。在前面的算法描述中，我提到取步长为1，但是实际上取值取决于数据样本，可以多取一些值，从大到小，分别运行算法，看看迭代效果，如果损失函数在变小，说明取值有效，否则要增大步长。前面说了。步长太大，会导致迭代过快，甚至有可能错过最优解。步长太小，迭代速度太慢，很长时间算法都不能结束。所以算法的步长需要多次运行后才能得到一个较为优的值。

（2）算法参数的初始值选择。 初始值不同，获得的最小值也有可能不同，因此梯度下降求得的只是局部最小值；当然如果损失函数是凸函数则一定是最优解。由于有局部最优解的风险，需要多次用不同初始值运行算法，关键损失函数的最小值，选择损失函数最小化的初值。

（3）归一化。由于样本不同特征的取值范围不一样，可能导致迭代很慢，为了减少特征取值的影响，可以对特征数据归一化，也就是对于每个特征x，求出它的期望x和标准差std(x)，然后转化为同一范围内的值。

 

5.其他优化算法对比

        原始的梯度下降方法有以下问题：在梯度平缓的维度下降非常慢，在梯度险峻的维度容易抖动，容易陷入局部极小值或鞍点。Zero gradient,gradient descent gets stuck （在高维空间中，鞍点比局部极小值更容易出现）选择一个合适的学习率可能是困难的。学习率太小会导致收敛的速度很慢，学习率太大会妨碍收敛，导致损失函数在最小值附近波动甚至偏离最小值。学习率调整试图在训练的过程中通过例如退火的方法调整学习率，即根据预定义的策略或者当相邻两代之间的下降值小于某个阈值时减小学习率。然而，策略和阈值需要预先设定好，因此无法适应数据集的特点对所有的参数更新使用同样的学习率。如果数据是稀疏的，同时，特征的频率差异很大时，我们也许不想以同样的学习率更新所有的参数，对于出现次数较少的特征，我们对其执行更大的学习率，下面的其他梯度算法是在梯度算法上进行了优化，具体如下：

冲量梯度下降算法（Momentum optimization）
        冲量梯度下降算法是BorisPolyak在1964年提出的，其基于这样一个物理事实：将一个小球从山顶滚下，其初始速率很慢，但在加速度作用下速率很快增加，并最终由于阻力的存在达到一个稳定速率。考虑这样一种情形，小球从山顶往下滚动，一开始很顺利，可是在接近最低点的时候，小球陷入了一段狭长的浅山谷，由于小球一开始并不是直接沿着山谷的方向滚下，因此小球会在这个浅浅的山谷中不断震荡——不断冲上墙壁，接着又从墙壁上滚下来，这种情况并不是我们想看到的，因为这增加了迭代时间，冲量(Momentnum)的引入，使得我们的目标更新的更快了，冲量的更新方式有以下两种，两种方式之间并无太大差异。

• 在每次下降时都加上之前运动方向上的动量
• 在梯度缓慢的维度下降更快，在梯度险峻的维度减少抖动

        对于在梯度点处具有相同的方向的维度，其动量项增大，对于在梯度点处改变方向的维度，其动量项减小。因此，我们可以得到更快的收敛速度，同时可以减少摇摆，具体下降过程如下两个图对比：

               

Nesterov Accelerated Gradient
       NAG算法全称Nesterov Accelerated Gradient，是YuriiNesterov在1983年提出的对冲量梯度下降算法的改进版本，其速度更快。然而，让一个小球盲目地沿着斜坡滚下山是不理想的，我们需要一个更聪明的球，它知道下一步要往哪里去，因此在斜坡有上升的时候，它能够自主调整方向。Nesterov Accelerated Gradient 是基于冲量梯度下降算法进行改进的一种算法，也是梯度下降算法的变种，我们利用动量项算来更新参数，通过计算能够告诉我们参数未来位置的一个近似值（梯度并不是完全更新），这也就是告诉我们参数大致将变为多少。通过计算关于参数未来的近似位置的梯度，而不是关于当前的参数的梯度，我们可以高效的求解。

                   

         动量法首先计算当前的梯度值（图中的小的蓝色向量），然后在更新的累积梯度（大的蓝色向量）方向上前进一大步，Nesterov加速梯度下降法NAG首先在先前累积梯度（棕色的向量）方向上前进一大步，计算梯度值，然后做一个修正（绿色的向量）。这个具有预见性的更新防止我们前进得太快，同时增强了算法的响应能力，这一点在很多的任务中对于RNN的性能提升有着重要的意义。
 

AdaGrad
        AdaGrad是Duchi在2011年提出的一种学习速率自适应的梯度下降算法。在训练迭代过程，其学习速率是逐渐衰减的，经常更新的参数其学习速率衰减更快，这是一种自适应算法。尽管我们可以根据损失函数的梯度来加快更新参数，我们也希望能够根据参数的重要性来决定其更新的幅度。AdaGrad是一种基于梯度算法的优化算法,它只做了一件事:根据参数来自适应调整学习率。对于不常出现的参数进行较大的更新，对于经常出现的参数进行较少的更新，因此，这种方法非常适合处理稀疏数据。在梯度大的维度，减小下降速度；在梯度小的维度，加快下降速度让学习率适应参数，对于出现次数较少的特征，我们对其采用更大的学习率，对于出现次数较多的特征，我们对其采用较小的学习率。因此，Adagrad非常适合处理稀疏数据。Adagrad算法的一个主要优点是无需手动调整学习率Adagrad的一个主要缺点是它在分母中累加梯度的平方：由于每增加一个正项，在整个训练过程中，累加的和会持续增长。这会导致学习率变小以至于最终变得无限小，在学习率无限小时，Adagrad算法将无法取得额外的信息。
 

AdaDelta

        AdaDelta是在AdaGrad的基础上发展而来的，目的是解决AdaGrad算法中学习率的单调减少问题。AdaDelta不再采用累积梯度平方和的方法来调整学习率，而是根据一些固定的w的大小来限制过去累积梯度的窗口