- 1PHP-搭建Web服务器_php搭建web服务器
- 2Istio系列学习(二)----Istio架构_istio和k8s区别
- 3Pytorch使用yolov3训练自己的数据进阶_best.pt可以继续训练吗
- 4【开题报告】基于SpringBoot的在线诊疗预约系统_springboot软件设计开题报告
- 5C++Qt开发——QSS样式表_background-color: rgb(240,241,242); border: 1px so
- 6【Labview-3D虚拟平台】Labview与Solidworks联合仿真(保姆级)(下)在Labview中使用Solidworks的3D模型——装配体、父级与子级_labview 三维图片导入的是个壳
- 7linux驱动-定时器_linux驱动关闭定时器
- 8ERROR 1226 (42000): User ‘root‘ has exceeded the ‘max_connections_per_hour‘ resource (current value:_user 'root' has exceeded the 'max_connections_per_
- 9HanLP Demo(学习笔记)_hanlp训练自己领域的模型
- 10python之OCR文字识别_python ocr
机器学习(五)之评价指标:二分类指标、多分类指标、混淆矩阵、不确定性、ROC曲线、AUC、回归指标_检验 二分类的正确性
赞
踩
0 本文简介
我们使用精度来评估分类性能,使用
R
2
R^2
R2评估回归性能,但是监督模型在给定数据集上的表现有多种方法。我们还有很多评估指标,本文简要介绍二分类指标、多分类指标,以及浅谈回归问题的评价问题。
相关笔记:
机器学习(一)之 2万多字的监督学习模型总结V1.0:K近邻、线性回归、岭回归、朴素贝叶斯模型、决策树、随机森林、梯度提升回归树、SVM、神经网络
机器学习(二)之无监督学习:数据变换、聚类分析
机器学习(三)之数据表示和特征工程:One-Hot编码、分箱处理、交互特征、多项式特征、单变量非线性变换、自动化特征选择
机器学习(四)之参数选择:交叉验证、网格搜索
机器学习(五)之评价指标:二分类指标、多分类指标、混淆矩阵、不确定性、ROC曲线、AUC、回归指标
1 二分类指标
对于二分类问题,我们通常会说正类(positive class)和反类(negative class),而正类是我们要寻找的类。在评估二分类问题时,往往会出现很多问题。
1.1 二分类时的错误类型
在二分类问题中,精度并不能很好地度量分类性能。比如,在使用模型诊断癌症时,如果测试结果为阴性,那么认为患者是健康的,而如果测试结果为阳性,患者则需要接受额外的筛查。这里我们将阳性测试结果(表示患有癌症)称为正类,将阴性测试结果称为反类。
一种可能的错误是健康的患者被诊断为阳性,导致需要进行额外的测试。这给患者带来了一些费用支出和不便(可能还有精神上的痛苦)。错误的阳性预测叫作假正例(false positive)。另一种可能的错误是患病的人被诊断为阴性,因而不会接受进一步的检查和治疗。未诊断出的癌症可能导致严重的健康问题,甚至可能致命。这种类型的错误(错误的阴性预测)叫作假反例(false negative)。在统计学中,假正例也叫作第一类错误(type I error),假反例也叫作第二类错误(type II error)。
1.2 不平衡的数据
如果在两个类别中,一个类别的出现次数比另一个多很多,那么错误类型将发挥重要作用。例如。我们一共有100个病人,其中99人是健康的(阴性、反类),1人是患癌症的(阳性、正类),那么这种数据集就是不平衡数据集(imbalanced dataset)或者具有不平衡类别的数据集(dataset with imbalanced classes)。在实际当中,不平衡数据才是常态。
在这个数据集中,我们即使预测得到99%的分类精度,也不代表我们模型的泛化性能就好。有一种可能·就是,我们把99个健康的预测正确了,而1个患病的没有预测正确,这会导致非常严重的后果,因此精度在这里就不适用了。
1.3 混淆矩阵
对于二分类问题的评估结果,一种最全面的表示方法是使用混淆矩阵(confusion matrix)。混淆矩阵主对角上的元素对应于正确的分类,而其他元素则告诉我们一个类别中有多少样本被错误地划分到其他类别中。混淆矩阵如下表所示:
| 预测为正类 | 预测为反类 | |
|---|---|---|
| 真实正类 | TP | FN |
| 真实反类 | FP | TP |
真正例(TP):true positive,将正类中正确分类的样本。
真反例(TN):true negative,将反类中正确分类的样本。
假正例(FP):false positive,反类预测为正类的样本。
假反例(FN):false negative,正类预测为反类的样本。
总结混淆矩阵包含信息的方法:
1、精度:正确预测的数量(TP 和TN)除以所有样本的数量(混淆矩阵中所有元素的总和)
A
c
c
u
r
a
c
y
=
T
P
+
T
N
T
P
+
T
N
+
F
P
+
F
N
Accuracy = \frac {TP + TN}{TP + TN + FP + FN}
Accuracy=TP+TN+FP+FNTP+TN
2、准确率:度量的是被预测为正例的样本中有多少是真正的正例
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
Precision = \frac {TP}{TP + FP}
Precision=TP+FPTP
如果目标是限制假正例的数量,那么可以使用准确率作为性能指标。准确率也被称为阳性预测值(positive
predictive value,PPV)。
3、召回率:度量的是正类样本中有多少被预测为正类
R
e
c
a
l
l
=
T
P
T
P
+
F
N
Recall = \frac {TP}{TP + FN}
Recall=TP+FNTP
如果我们需要找出所有的正类样本,即避免假反例是很重要的情况下,那么可以使用召回率作为性能指标.。召回率又称为灵敏度(sensitivity)、命中率(hit rate)和真正例率(true positive rate,TPR)。
在优化召回率与优化准确率之间需要折中。如果我们预测所有样本都属于正类,那么可以轻松得到完美的召回率——没有假反例,也没有真反例。但是,将所有样本都预测为正类,将会得到许多假正例,因此准确率会很低。反之,准确率将会很完美,但是召回率会非常差。
4、f-分数
将准确率和召回率进行汇总的一种方法是f-分数(f-score)或f-度量(f-measure),它是准确率与召回率的调和平均:
F
=
2
⋅
p
r
e
c
i
s
i
o
n
⋅
r
e
c
a
l
l
p
r
e
c
i
s
i
o
n
+
r
e
c
a
l
l
F = 2\cdot \frac {precision \cdot recall}{precision + recall}
F=2⋅precision+recallprecision⋅recall
实际上,
F
=
2
⋅
T
P
2
⋅
T
P
+
F
N
+
F
P
F = \frac {2\cdot TP}{2\cdot TP +FN + FP}
F=2⋅TP+FN+FP2⋅TP
也被称为f1-分数(f1-score)。由于同时考虑了准确率和召回率,所以它对于不平衡的二分类数据集来说是一种比精度更好的度量。f- 分数似乎比精度更加符合我们对好模型的直觉。然而,f- 分数的一个缺点是比精度更加难以解释。
可以使用classification_report这个函数,同时计算准确率、召回率和f1- 分数,并以美观的格式打印出来。但是选择哪个类作为正类对指标有很大影响。
1.4 考虑不确定性
大多数分类器都提供了一个decision_function或predict_proba方法来评估预测的不确定度。预测可以被看作是以某个固定点作为decision_function或predict_proba输出的阈值——在二分类问题中,我们使用0 作为决策函数的阈值,0.5 作为predict_proba的阈值。
如果准确率比召回率更重要,或者反过来,或者数据严重不平衡,那么改变决策阈值是得到更好结果的最简单方法。由于decision_function的取值可能在任意范围,所以很难提供关于如何选取阈值的经验法则。 对于实现了predict_proba 方法的模型来说,选择阈值可能更简单,因为predict_proba 的输出固定在0 到1 的范围内,表示的是概率。默认情况下,0.5 的阈值表示,如果模型以超过50% 的概率“确信”一个点属于正类,那么就将其划为正类。增大这个阈值意味着模型需要更加确信才能做出正类的判断(较低程度的确信就可以做出反类的判断)。
1.5 准确率-召回率曲线
改变模型中用于做出分类决策的阈值,是一种调节给定分类器的准确率和召回率之间折中的方法。对分类器设置要求(比如90% 的召回率)通常被称为设置工作点(operating point)。利用**准确率- 召回率曲线(precision-recall curve)**可以同时查看所有可能的阈值或准确率和召回率的所有可能折中。sklearn.metrics模块可以绘制这个条曲线。precision_recall_curve函数返回一个列表,包含按顺序排序的所有可能阈值(在决策函数中出现的所有值)对应的准确率和召回率,这样我们就可以绘制准确率- 召回率曲线。

黑色圆圈表示的是阈值为0 的点,0 是decision_function 的默认阈值。这个点是在调用predict 方法时所选择的折中点。
曲线越靠近右上角,则分类器越好。 右上角的点表示对于同一个阈值,准确率和召回率都很高。曲线从左上角开始,这里对应于非常低的阈值,将所有样本都划为正类。提高阈值可以让曲线向准确率更高的方向移动,但同时召回率降低。继续增大阈值,大多数被划为正类的点都是真正例,此时准确率很高,但召回率更低。随着准确率的升高,模型越能够保持较高的召回率,则模型越好。总结准确率—召回率曲线的一种方法是计算该曲线下的积分或面积,也叫作平均准确率(average precision)。
准确率- 召回率曲线下的面积与平均准确率之间还有一些较小的技术区别。但这个解释表达的是大致思路。
1.6 ROC与AUC
受试者工作特征曲线(receiver operating characteristics curve),简称为ROC 曲线(ROC curve)。与准确率- 召回率曲线类似,ROC 曲线考虑了给定分类器的所有可能的阈值,但它显示的是假正例率(false positive rate,FPR)和真正例率(true positive rate,TPR),而不是报告准确率和召回率。真正例率只是召回率的另一个名称,而假正例率则是假正例占所有反类样本的比例:
F
P
R
=
F
P
F
P
+
T
N
FPR = \frac {FP}{FP + TN}
FPR=FP+TNFP
我们可以用roc_curve 函数来计算ROC 曲线。对ROC曲线,理想的曲线要靠近左上角:希望分类器的召回率很高,同时保持假正例率很低。最接近左上角的点可能是比默认选择更好的工作点。同样请注意,不应该在测试集上选择阈值,而是应该在单独的验证集上选择。
我们通常使用ROC 曲线下的面积AUC(area under the curve) 来总结ROC曲线的信息。我们可以利用roc_auc_score函数来计算ROC 曲线下的面积。对于不平衡的分类问题来说,AUC 是一个比精度好得多的指标。AUC 可以被解释为评估正例样本的排名(ranking)。它等价于从正类样本中随机挑选一个点,由分类器给出的分数比从反类样本中随机挑选一个点的分数更高的概率。因此,AUC 最高为1,这说明所有正类点的分数高于所有反类点。对于不平衡类别的分类问题,使用AUC 进行模型选择通常比使用精度更有意义。AUC 没有使用默认阈值,因此,为了从高AUC 的模型中得到有用的分类结果,可能还需要调节决策阈值。
2 多分类指标
多分类问题的所有指标基本上都来自于二分类指标,但是要对所有类别进行平均。多分类的精度被定义为正确分类的样本所占的比例。同样,如果类别是不平衡的,精度并不是很好的评估度量。除了精度,常用的工具有混淆矩阵和分类报告。
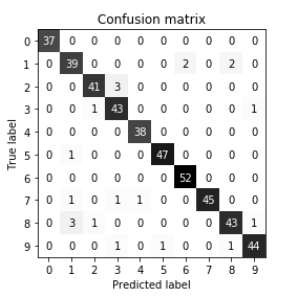
对于多分类问题中的不平衡数据集,最常用的指标就是多分类版本的f- 分数。多分类f- 分数背后的想法是,对每个类别计算一个二分类f- 分数,其中该类别是正类,其他所有类别组成反类。然后,使用以下策略之一对这些按类别f- 分数进行平均。
“宏”(macro)平均:计算未加权的按类别f- 分数。它对所有类别给出相同的权重,无论类别中的样本量大小。
“加权”(weighted)平均:以每个类别的支持作为权重来计算按类别f- 分数的平均值。分类报告中给出的就是这个值。
“微”(micro)平均:计算所有类别中假正例、假反例和真正例的总数,然后利用这些计数来计算准确率、召回率和f- 分数。
如果对每个样本等同看待,那么推荐使用“微”平均f1- 分数;如果对每个类别等同看待,那么推荐使用“宏”平均f1- 分数
3 回归指标
对回归问题可以像分类问题一样进行详细评估,例如,对目标值估计过高与目标值估计过低进行对比分析。但是,对于我们见过的大多数应用来说,使用默认R2 就足够了,它由所有回归器的score 方法给出。业务决策有时是根据均方误差或平均绝对误差做出的,这可能会鼓励人们使用这些指标来调节模型。但是一般来说,我们认为R2 是评估回归模型的更直观的指标。
4 在模型选择中使用评估指标
实际中我们通常希望,在使用GridSearchCV 或cross_val_score 进行模型选择时能够使用AUC等指标。scikit-learn 提供了一种非常简单的实现方法,就是scoring 参数,它可以同时用于GridSearchCV 和cross_val_score。
对于分类问题,scoring 参数最重要的取值包括:accuracy(默认值)、roc_auc、average_precision(准确率- 召回率曲线下方的面积)、f1、f1_macro、f1_micro 和f1_weighted
对于回归问题,最常用的取值包括: r 2 r^2 r2、mean_squared_error(均方误差)和mean_absolute_error(平均绝对误差)。我们可以查看metrics.scorer 模块中定义的SCORER 字典。


