2023华数杯数学建模竞赛C题思路解析_2023建模竞赛c题

如下为：2023华数杯数学建模竞赛C题 母亲身心健康对婴儿成长的影响 的思路解析

C题 母亲身心健康对婴儿成长的影响

母亲是婴儿生命中最重要的人之一，她不仅为婴儿提供营养物质和身体保护，还为婴儿提供情感支持和安全感。母亲心理健康状态的不良状况，如抑郁、焦虑、 压力等，可能会对婴儿的认知、情感、社会行为等方面产生负面影响。压力过大的母亲可能会对婴儿的生理和心理发展产生负面影响，例如影响其睡眠等方面。

附件给出了包括 390名 3 至 12 个月婴儿以及其母亲的相关数据。这些数据涵盖各种主题，母亲的身体指标包括年龄、婚姻状况、教育程度、妊娠时间、 分娩方式，以及产妇心理指标CBTS（分娩相关创伤后应激障碍问卷）、EPDS （爱丁堡产后抑郁量表）、HADS（医院焦虑抑郁量表）和婴儿睡眠质量指标包括整晚睡眠时间、睡醒次数和入睡方式。

背景分析：从背景中可以看出，本题主要解决母亲身心健康对婴儿成长的影响，我们需要通过对题目给的附件进行数据分析，来确定问题结果。这里就代表不能使用除附件外的自己找的数据了。为了对题目更好的分析。我们首先来分析一下附件数据。

如图为附件指标：

我们可以看出，婴儿行为为非数值型数据，这时我们需要先处理为数值型。对于非数值型数据进行量化，大家可以使用以下方法：

1标签编码

标签编码是将一组可能的取值转换成整数，从而对非数值型数据进行量化的一种方法。例如，在机器学习领域中，对于一个具有多个类别的变量，我们可以给每个类别赋予一个唯一的整数值，这样就可以将其转换为数值型数据。

2独热编码onehot

独热编码是将多个可能的取值转换成二进制数组的一种方法。在独热编码中，每个可能取值对应一个长度为总共可能取值个数的二进制数组，其中只有一个元素为1，其余元素均为0。例如，对于一个性别变量，可以采用独热编码将“男”和“女”分别转换为[1, 0]和[0, 1]。

3分类计数

分类计数是将非数值型数据转换为数值型数据的一种简单方法。在分类计数中，我们根据某些特定属性（比如学历、职业等）来对数据进行分类，然后统计每个类别的数量或频率。例如，在调查问卷中，我们可以对某个问题的回答按照“是”、“否”和“不确定”三个类别进行分类，并计算每个类别的数量或频率。

4主成分分析

主成分分析是将多维数据转换为低维度表示的一种方法。在主成分分析中，我们通过找到最能解释数据变异的主成分来对原始数据进行降维处理。这样就可以将非数值型数据转换为数值型数据。

这里建议使用标签编码/独热编码，最好使用标签编码，因为这个指标的数据是存在大小关系的。

另外，对于整晚睡眠时间，需要将其转换为数值型数据，也就是比如10:30，需要转换为10.5，这样方便后续进行计算分析。

数据预处理另一个很重要的步骤是：归一化处理，以避免量纲对建模结果的影响，如下是数据归一化的代码：

import pandas as pd
from sklearn.preprocessing import MinMaxScaler
 
# 读取数据
data = pd.read_excel('your_dataset.xlsx')
 
# 提取需要进行归一化的指标列
features_to_normalize = ['age', 'education', 'pregnancy_time', 'CBTS', 'EPDS', 'HADS', 'sleep_duration', 'awakening_times']
 
# 使用MinMaxScaler进行归一化
scaler = MinMaxScaler()
data[features_to_normalize] = scaler.fit_transform(data[features_to_normalize])
 
# 输出归一化后的数据
print(data)

上面的代码需要将your_dataset.xlsx替换为你的数据集文件名。features_to_normalize列表中包含了需要进行归一化处理的指标列名。

这里就对数据进行完初步的预处理了，开始看题！

请查阅相关文献，了解专业背景，根据题目数据建立数学模型，回答下列问题。

1. 许多研究表明，母亲的身体指标和心理指标对婴儿的行为特征和睡眠质量有影响，请问是否存在这样的规律，根据附件中的数据对此进行研究。

问题1分析：题目问的是母亲的身体指标和心理指标对婴儿的行为特征和睡眠质量是否有影响，这里要注意，题目没有明确说明什么才是这些指标，所以我们需要把题目附件指标与问题相互对应。建立母亲的身体指标模型、心理指标模型，婴儿的行为特征模型以及睡眠质量模型，这里需要大家自己考虑附件哪些指标是直接相关的。我在这里说明一下确定后我们需要怎样去建立这些模型，通常的方法有：

l 主成分分析（Principal Component Analysis，PCA）：PCA是一种线性降维方法，通过找到数据集中最重要的主成分来实现降维。它将原始数据投影到新的正交坐标系中，使得新坐标系上方差最大化，从而保留了数据中最具信息量的特征。

l 线性判别分析（Linear Discriminant Analysis，LDA）：LDA也是一种线性降维方法，但与PCA不同，LDA是一种监督学习方法，主要用于分类任务。它在降维的同时，试图最大化类间距离并最小化类内距离，以获得一个更具判别性能的低维表示。

l 局部线性嵌入（Locally Linear Embedding，LLE）：LLE是一种非线性降维方法，通过在局部区域内保持样本之间的线性关系来构建低维表示。LLE假设数据在高维空间中局部上是线性可分的，并通过重构每个样本与其邻居之间的线性关系，将高维数据映射到低维空间。

l 非负矩阵分解（Non-negative Matrix Factorization，NMF）：NMF是一种用于非负数据的降维方法。它将原始数据矩阵分解为两个非负矩阵的乘积，从而得到潜在的特征表示。NMF常用于图像处理和文本挖掘等领域。

l t-SNE：t-SNE是一种流行的非线性降维方法，用于可视化高维数据。它通过保持样本之间的局部相似性来将高维数据映射到二维或三维空间中。t-SNE能够很好地展示数据中的类别结构和聚类模式。

这里给出PCA的代码：

from sklearn.decomposition import PCA
import numpy as np
 
# 假设我们有一个数据集 X，其中每一行表示一个样本，每一列表示一个特征
X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
 
# 创建PCA对象，并指定要保留的主成分数量
pca = PCA(n_components=2)
 
# 对数据进行降维
X_pca = pca.fit_transform(X)
 
# 输出降维后的结果
print(X_pca)

在上述代码中，首先导入了PCA类和numpy库。然后，定义了一个包含样本的二维数组X。接下来，创建了一个PCA对象，并通过n_components参数指定要保留的主成分数量为2。然后，使用fit_transform方法对数据进行降维得到X_pca，它表示降维后的数据集。

然后可以使用一些可视化方法，来直观展示降维后的结果。如下为可能的可视化方法：

l 散点图：对于二维或三维的数据集，我们可以通过散点图将降维后的数据可视化。如果我们只保留了两个主成分，我们可以使用散点图将样本在这两个主成分上的投影呈现出来。不同类别的样本可以使用不同的颜色或符号进行区分，以便更好地理解数据的分布情况。

l 3D 散点图：如果我们保留了三个主成分，我们可以使用三维散点图将样本在这三个主成分上的投影呈现出来。这可以帮助我们更好地观察数据在多个维度上的分布情况。

l 可解释方差比例图：可解释方差比例图显示了每个主成分所解释的总方差的比例。通过绘制累积方差比例曲线，我们可以确定需要保留的主成分数量，以保留足够的信息量。该图可以帮助我们选择合适的主成分数量来进行降维。

l 生物特征图（Biplot）：生物特征图结合了原始特征和主成分之间的关系。在二维降维情况下，我们可以将原始特征显示为箭头，并将主成分的投影表示为点。这样可以更好地理解原始特征如何与主成分相关。

在得到题目所需要的四个特征后，对其进行相关性分析/关联分析，即可得到最后的影响关系。这时最好绘制热力图来直观展示影响情况。如下是pyrhon的热力图代码：

import seaborn as sns
import numpy as np
 
# 假设我们有一个二维数据集 data
data = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
 
# 使用Seaborn绘制热力图
sns.heatmap(data)
 
# 显示图形
plt.show()

如果想绘制更好看的，可以在网上查找：python热力图绘制代码即可。

2. 婴儿行为问卷是一个用于评估婴儿行为特征的量表，其中包含了一些关于婴儿情绪和反应的问题。我们将婴儿的行为特征分为三种类型：安静型、中等型、矛盾型。请你建立婴儿的行为特征与母亲的身体指标与心理指标的关系模型。 数据表中最后有20组（编号391-410号）婴儿的行为特征信息被删除，请你判断他们是属于什么类型。

问题2分析：问题2很明显是需要建立一个预测模型，需要我们定义好自变量和因变量，然后用合适的模型算法建立这两者之间的关系。推荐的方法有：多元线性回归、随机森林、神经网络、非线性拟合等方法。这里一定要用到我前面提到的，对婴儿的行为特征进行量化处理。（推荐设置为1，2，3，理由之前说了）之后就很好办了，这些方法都是很好的预测方法，我认为题目较为简单，可以不使用复杂算法，多元线性回归即可解决。如下是多元线性回归的相关代码：

import statsmodels.api as sm
import pandas as pd
 
# 假设我们有一个包含多个特征和目标变量的数据集 data，其中每一行表示一个样本
data = pd.DataFrame({'x1': [1, 2, 3, 4, 5],
                     'x2': [6, 7, 8, 9, 10],
                     'y': [11, 12, 13, 14, 15]})
 
# 提取自变量（特征）和因变量（目标变量）
X = data[['x1', 'x2']]
y = data['y']
 
# 添加常数列作为截距项，如果你不需要截距项，可以省略此步骤
X = sm.add_constant(X)
 
# 创建多元线性回归模型并拟合数据
model = sm.OLS(y, X)
results = model.fit()
 
# 输出回归模型的详细结果
print(results.summary())

3. 对母亲焦虑的干预有助于提高母亲的心理健康水平，还可以改善母婴交互质量，促进婴儿的认知、情感和社交发展。CBTS、EPDS、HADS的治疗费用相对于患病程度的变化率均与治疗费用呈正比，经调研，给出了两个分数对应的治疗费用，详见表1。现有一个行为特征为矛盾型的婴儿，编号为238。请你建立模型，分析最少需要花费多少治疗费用，能够使婴儿的行为特征从矛盾型变为中等型？若要使其行为特征变为安静型，治疗方案需要如何调整？

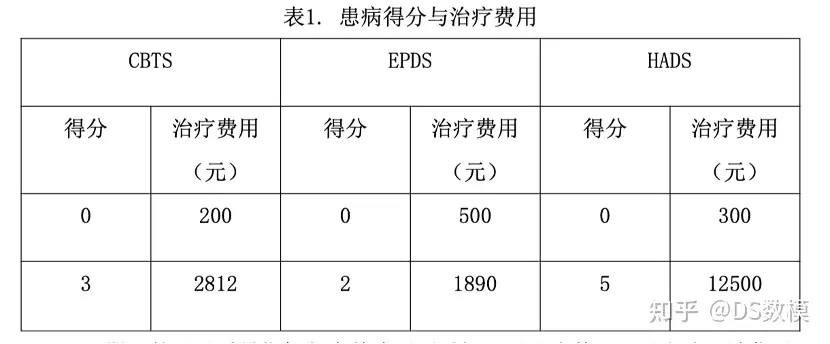
问题3分析：这道题目要注意的是，题目要求的是要分析最少的消耗，那么我们在限定阈值的时候就可以相对宽松一点。可以设置置信区间。

题目说明了是呈正比的，那么我们需要假设具体的正比关系，比如线性相关/非线性，实际此题为多目标规划问题，可以从前面建立的模型入手，算出具体238号是多少分？尽量在2.5-3.5之间，然后看他如何调整其他指标后，可以在得分低的情况下，治疗费用尽可能少。也就是以这两者为目标，建立目标函数即可。如下给大家简单介绍下多目标规划的步骤：

l 确定目标：明确问题中的多个目标函数，并将其形式化表示。

l 确定决策变量：确定可以调整的决策变量，这些变量将影响目标函数的值。

l 定义约束条件：确定限制决策变量的约束条件，包括等式约束和不等式约束，以满足实际问题的限制。

l 建立数学模型：将目标函数和约束条件转化为数学模型，以便进行优化求解。这通常涉及到数学表达式、线性规划、非线性规划等技术。

l 选择优化算法：根据问题的特点（如凸性、可微性等），选择适合的优化算法来求解多目标规划问题。常见的算法包括遗传算法、粒子群算法、线性规划算法等。

l 求解优化问题：利用选择的优化算法，对建立的数学模型进行求解，得到一组最优的决策变量值。

l 解释并评估结果：对求解结果进行解释和评估，分析每个目标函数的最优值及其对应的决策变量值。

l 制定权衡方案：根据实际需求和问题特点，制定权衡方案来选择最终的解决方案。这可能涉及到权重分配、敏感性分析、偏好排序等方法。

l 效果验证：将确定的解决方案在实践中执行，并对结果进行评估和验证，以确保其有效性和可行性。

然后就是代码了，给大家一个matlab的多目标规划代码：（建议也可以用lingo进行求解）

from pyomo.environ import *
 
# 创建一个具体模型
model = ConcreteModel()
 
# 定义决策变量
model.x = Var(within=NonNegativeReals)
model.y = Var(within=NonNegativeReals)
 
# 定义目标函数
model.obj1 = Objective(expr=model.x + 2*model.y, sense=minimize)
model.obj2 = Objective(expr=3*model.x + model.y, sense=minimize)
 
# 定义约束条件
model.con1 = Constraint(expr=2*model.x + model.y >= 1)
model.con2 = Constraint(expr=model.x - model.y <= 2)
 
# 求解多目标规划问题
opt = SolverFactory('glpk')
results = opt.solve(model)
 
# 输出结果
print("Decision Variables:")
print("x =", model.x.value)
print("y =", model.y.value)
print("Objectives:")
print("Objective 1 =", model.obj1.expr())
print("Objective 2 =", model.obj2.expr())

我们首先创建了一个结构体problem，用于存储优化问题的参数。

然后，我们使用匿名函数@(x)来定义目标函数。这里的目标函数返回一个列向量，其中第一个元素为第一个目标函数的值，第二个元素为第二个目标函数的值。

接着，我们设置初始解x0、变量下界lb、线性不等式约束矩阵Aineq和线性不等式约束向量bineq。

最后，我们调用multiobjective函数来求解多目标优化问题，并将结果存储在result变量中。

通过输出结果，我们可以得到决策变量x的取值以及各个目标函数的最优值。

4. 婴儿的睡眠质量指标包含整晚睡眠时间、睡醒次数、入睡方式。请你对 婴儿的睡眠质量进行优、良、中、差四分类综合评判，并建立婴儿综合睡眠质量 与母亲的身体指标、心理指标的关联模型，预测最后20组（编号391-410号）婴 儿的综合睡眠质量。

4-5问及其他助攻（代码、可视化方法、论文、讲解视频等）请看文末

选题建议如下：2023华数杯数学建模竞赛选题建议_DS数模的博客-CSDN博客