【论文翻译】Many-Class Few-Shot Learning on Multi-Granularity Class Hierarchy_few-shot inductive learning on temporal knowledge

Many-Class Few-Shot Learning on Multi-Granularity Class Hierarchy

多粒度类层次上的多类少样本学习

摘要

We study many-class few-shot (MCFS) problem in both supervised learning and meta-learning settings. Compared to the well-studied many-class many-shot and few-class few-shot problems, the MCFS problem commonly occurs in practical applications but has been rarely studied in previous literature. It brings new challenges of istinguishing between many classes given only a few training samples per class. In this article, we leverage the class hierarchy as a prior knowledge to train a coarse-to-fine classifier that can produce accurate predictions for MCFS problem in both settings. The propose model, “memory-augmented hierarchical-classification network (MahiNet)”, performs coarse-to-fine classification where each coarse class can cover multiple fine classes. Since it is challenging to directly distinguish a variety of fine classes given few-shot data per class, MahiNet starts from learning a classifier over coarse-classes with more training data whose labels are much cheaper to obtain. The coarse classifier reduces the searching range over the fine classes and thus alleviates the challenges from “many classes”. On architecture, MahiNet first deploys a convolutional neural network (CNN) to extract features. It then integrates a memory-augmented attention module and a multi-layer perceptron (MLP) together to produce the probabilities over coarse and fine classes. While the MLP extends the linear classifier, the attention module extends the KNN classifier, both together targeting the “few-shot” problem. We design several training strategies of MahiNet for supervised learning and meta-learning. In addition, we propose two novel benchmark datasets “mcfsImageNet” (as a subset of ImageNet) and “mcfsOmniglot” (re-splitted Omniglot) specially designed for MCFS problem. In experiments, we show that MahiNet outperforms several state-of-the-art models (e.g., prototypical networks and relation networks) on MCFS problems in both supervised learning and meta-learning.

我们研究了监督学习和元学习环境下的多类少样本（MCFS）问题。与研究较多的多类多样本问题和少类少样本问题相比，MCFS问题在实际应用中普遍存在，但在以往的文献中很少被研究。它带来了新的挑战，即在每类只提供少量训练样本的情况下，在多个类之间进行区分。在本文中，我们利用类层次结构作为先验知识来训练一个从粗到细的分类器，该分类器可以在这两种情况下为MCFS问题生成准确的预测。提出的模型“记忆增强层次分类网络（MahiNet）”执行从粗到细的分类，其中每个粗分类可以覆盖多个细分类。由于在每个类只有很少的样本数据的情况下，直接区分各种精细类是一个挑战，因此MahiNet从学习分类器开始，而不是学习具有更多训练数据的粗糙类，这些训练数据的标签获取成本要低得多。粗分类器缩小了细类的搜索范围，从而减轻了“多类”的挑战。在体系结构方面，MahiNet首先部署了卷积神经网络（CNN）来提取特征。然后，它将一个增强记忆的注意模块和一个多层感知器（MLP）集成在一起，生成粗类和细类的概率。MLP扩展了线性分类器，而注意模块扩展了KNN分类器，两者都针对“少样本”问题。我们设计了几种MahiNet的训练策略，用于监督学习和元学习。此外，我们还针对MCFS问题提出了两个新的基准数据集“mcfsImageNet”（作为ImageNet的子集）和“mcfsOmniglot”（重新拆分的Omniglot）。在实验中，我们发现MahiNet在监督学习和元学习中的MCFS问题上都优于几种最先进的模型（例如原型网络和关系网络）。

1介绍

The representation power of deep neural networks (DNN) has significantly improved in recent years, as deeper, wider and more complicated DNN architectures have merged to match the increasing computation power of new hardware [1], [2]. Although this brings hope to complex tasks that could be hardly solved by previous shallow models, more labeled data is usually required to train the deep models. The scarcity of annotated data has become a new bottleneck for training more powerful DNNs. It is quite common in practical applications such as image search, robot navigation and video surveillance. For example, in image classification, the number of candidate classes easily exceeds tens of thousands (i.e., many-class), but the training samples available for each class can be less than 100 (i.e., few-shot). Unfortunately, this scenario is beyond of the scope of current meta-learning methods for few-shot classification, which aims to address the data scarcity (few-shot data per class) but the number of classes in each task is usually less than 10. Additionally, in life-long learning, models are always updated once new training data becomes available, and those models are expected to quickly adapt to new classes with a few training samples available.

近年来，随着更深、更广、更复杂的DNN体系结构的融合，以匹配新硬件不断增长的计算能力，深度神经网络（DNN）的表示能力显著提高[1]，[2]。虽然这给以前的浅层模型难以解决的复杂任务带来了希望，但通常需要更多的标记数据来训练深层模型。注释数据的稀缺性已成为训练更强大的DNN的新瓶颈。它在图像搜索、机器人导航和视频监控等实际应用中非常常见。例如，在图像分类中，候选类的数量很容易超过数万（即许多类），但每个类的可用训练样本可以少于100（即很少的样本）。不幸的是，这种情况超出了当前少样本分类元学习方法的范围，该方法旨在解决数据稀缺问题（每个类的镜头数据很少），但每个任务中的类数通常少于10。此外，在终身学习中，一旦有了新的训练数据，模型总是会被更新，而且这些模型预计会在只有少量训练样本的情况下快速适应新类别。

Although previous works of fully supervised learning have shown the remarkable power of DNN when manyclass many-shot” training data is available, their performance degrades dramatically when each class only has a few samples available for training. In practical applications, acquiring samples of rare species or personal data from edge devices is usually difficult, expensive, and forbidden due to privacy protection. In many-class cases, annotating even one additional sample per class can be very expensive and requires a lot of human efforts. Moreover, the training set cannot be fully balanced over all the classes in practice. In these few-shot learning scenarios, the capacity of a deep model cannot be fully utilized, and it becomes much harder to generalize the model to unseen data. Recently, several approaches have been proposed to address the few-shot learning problem. Most of them are based on the idea of “meta-learning”, which trains a meta-learner over different few-shot tasks so it can generalize to new few-shot tasks with unseen classes. Thereby, the meta-learner aims to learn a stronger prior encoding the general knowledge achieved during learning various tasks, so it is capable to help a learner model quickly adapt to a new task with new classes of insufficient training samples. Meta-learning can be categorized into two types: methods based on “learning to optimize”, and methods based on metric learning. The former type adaptively modifies the optimizer (or some parts of it) used for training the task-specific model.  It includes methods that incorporate an Recurrent Neural Networks (RNN) meta-learner [3], [4], [5], and model-agnostic meta-learning (MAML) methods aiming to learn a generally compelling initialization [6]. The second type learns a similarity/distance metric [7] or a model generating a support set of samples [8] that can be used to build K-Nearest Neighbors (KNN) classifiers from few-shot data in different tasks.

尽管之前的全监督学习研究已经表明，当多类多样本训练数据可用时，DNN具有显著的能力，但当每个类只有少量样本可供训练时，DNN的性能会急剧下降。在实际应用中，从边缘设备获取稀有物种样本或个人数据通常比较困难、昂贵，并且由于隐私保护而被禁止。在许多类的情况下，为每个类添加一个额外的示例可能非常昂贵，并且需要大量的人力。此外，在实践中，训练集不能在所有类别中完全平衡。在这些少样本学习场景中，深度模型的容量无法得到充分利用，并且很难将模型推广到看不见的数据。最近，人们提出了几种方法来解决少样本学习问题。其中大多数都基于“元学习”的思想，即在不同的少样本任务中训练元学习者，这样就可以推广到新的少样本任务和看不见的类。因此，元学习者的目标是对学习各种任务期间获得的一般知识进行更强的先验编码，从而能够帮助学习者模型快速适应训练样本不足的新任务。元学习可以分为两类：基于“学习优化”的方法和基于度量学习的方法。前一种类型自适应地修改用于训练特定于任务的模型的优化器（或其某些部分）。它包括结合了递归神经网络（RNN）元学习器[3]、[4]、[5]和模型不可知元学习（MAML）方法的方法，旨在学习一个普遍令人信服的初始化[6]。第二种类型学习相似性/距离度量[7]或生成样本支持集[8]的模型，这些样本可用于从不同任务中的少量样本数据构建K-最近邻（KNN）分类器。

Instead of meta-learning methods, data augmentation based approaches, such as the hallucination method proposed in [9], address the few-shot learning problem by generating more artificial samples for each class. However, most existing few-shot learning approaches only focus on “few-class” cases (e.g., 5 or 10) per task, and their performance drastically collapses when the number of classes slightly grows to tens to hundreds. This is because the samples per class no longer provide enough information to distinguish them from other possible samples within a large number of other classes. And in real-world few-shot problems, a task is usually complicated involving many classes.

与元学习方法不同，基于数据增强的方法，如[9]中提出的幻觉方法，通过为每个类生成更多人工样本来解决少样本学习问题。然而，大多数现有的少样本学习方法只关注每个任务的“少类”情况（例如，5或10），当类的数量略微增加到几十到几百个时，它们的性能会急剧下降。这是因为每个类的样本不再提供足够的信息来将它们与大量其他类中的其他可能样本区分开来。而在现实世界中，一项任务通常是复杂的，涉及很多类。

Fortunately, in practice, multi-outputs/labels information such as coarse-class labels in a class hierarchy is usually available or cheaper to obtain. In this case, the correlation between fine and coarse classes can be leveraged in solving the MCFS problem, e.g., by training a coarse-to-fine hierarchical prediction model. As shown in Fig. 1, coarse class labels might reveal the relationships among the targeted fine classes. Moreover, the samples per coarse class are sufficient to train a reliable coarse classifier, whose predictions are able to narrow down the candidates for the corresponding fine class. For example, a sheepdog with long hair could be easily mis-classified as a mop when training samples of sheepdog are insufficient. However, if we could train a reliable dog classifier, it would be much simpler to predict an image as a sheepdog than a mop given a correct prediction of the coarse class as “dog”. Training coarse-class prediction models is much easier and less suffered from the “many class few shot”problem (since the coarse classes are fewer than the fine classes and the samples per coarse class are much more than that for each fine class). It provides helpful information to fine-class prediction due to the relationship between coarse classes and fine classes. Hence, class hierarchy might provide weakly supervised information to help solve the “many-class few-shot (MCFS)” problem in a framework of multi-output learning, which aims to predict the class label on each level of the class hierarchy.

幸运的是，在实践中，多输出/标签信息（例如类层次结构中的粗略类标签）通常是可用的，或者获取成本较低。在这种情况下，可以利用精细类和粗糙类之间的相关性来解决MCFS问题，例如，通过训练从粗到细的层次预测模型。如图1所示，粗类标签可能会揭示目标细类之间的关系。此外，每个粗类的样本足以训练出可靠的粗分类器，其预测能够缩小相应细类的候选范围。例如，当牧羊犬的训练样本不足时，长发牧羊犬很容易被误归类为拖把。然而，如果我们能够训练出一个可靠的狗分类器，那么在正确预测粗类为“狗”的情况下，预测一张牧羊犬图像要比预测一张拖把图像简单得多。训练粗类预测模型要容易得多，而且较少受到“多类少样本”问题的影响（因为粗类比细类少，每个粗类的样本比每个细类的样本多）。由于粗类和细类之间的关系，它为细类预测提供了有用的信息。因此，在多输出学习的框架下，类层次结构可以提供弱监督信息来帮助解决“多类少样本”（MCFS）问题，该框架旨在预测类层次结构每一层上的类标签。

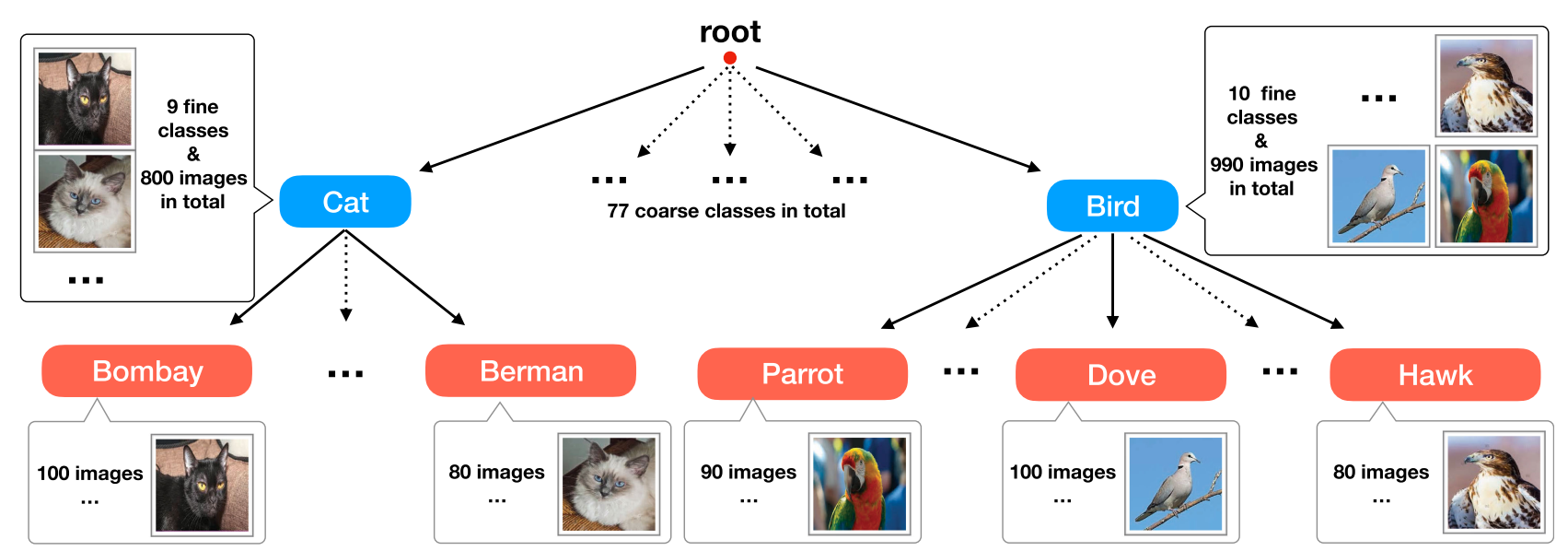
Fig. 1. A many-class few-shot learning (MCFS) problem using multi-label class hierarchy information. There are a few coarse classes (blue) and each coarse class covers a large number of fine classes (red) so that the total number of fine classes is large. Only a few training samples are available for each fine class. The goal is to train a classifier to enerate a prediction over all fine classes with the help of coarse prediction. We utilize meta-learning to solve the problem of many-class few-shot learning problem, where each task is an MCFS problem sampled from a certain distribution. The meta-learner’s goal is to help train a classifier for any sampled task with better adaptation to few-shot data within the sampled task. 利用多标签类层次信息的多类少样本学习（MCFS）问题。有几个粗类（蓝色），每个粗类覆盖大量细类（红色），因此细类的总数很大。每个类别只有几个训练样本可用。目标是训练分类器在粗预测的帮助下对所有精细类生成预测。我们利用元学习来解决多类少样本学习问题，其中每个任务都是从特定分布中抽样的MCFS问题。元学习者的目标是帮助为任何采样任务训练分类器，更好地适应采样任务中的少量样本数据。

In this paper, we address the MCFS problem in both traditional supervised learning and in meta-learning setting by exploring the multi-output information on multiple class hierarchy levels. We develop a neural network architecture “memory-augmented hierarchical-classification networks(MahiNet)” that can be applied to both learning settings. MahiNet uses a Convolutional Neural Network (CNN), i.e., ResNet [1], as a backbone network to first extract features from raw images. It then trains coarse-class and fine-class classifiers based on the features, and combines their outputs to produce the final probability prediction over the fine classes. In this way, both the coarse-class and the fine-class classifiers mutually help each other within MahiNet: the coarse classifier helps to narrow down the candidates for the fine classifier, while the fine classifier provides multiple attributes describing every coarse class and can regularize the coarse classifier. This design leverages the relationship between the fine classes as well as the relationship between the fine classes and the coarse classes, which mitigates the difficulty caused by the “many class” challenge. To the best of our knowledge, we are the first to successfully train a multi-output model to employ existing class hierarchy prior for improving both few-shot learning and supervised learning. It is different from those methods discussed in related works that use a latent clustering hierarchy instead of the explicit class hierarchy we use. In Table 1, we provide a brief comparison of MahiNet with other popular models on the learning scenarios they excel.

在本文中，我们通过探索多个类层次上的多输出信息来解决传统监督学习和元学习环境下的MCFS问题。我们开发了一种神经网络结构“记忆增强层次分类网络（MahiNet）”，可以应用于两种学习环境。MahiNet使用卷积神经网络（CNN），即ResNet[1]作为主干网络，首先从原始图像中提取特征。然后，它根据特征训练粗类和细类分类器，并结合它们的输出对细类进行最终概率预测。通过这种方式，粗类和细类分类器在MahiNet中相互帮助：粗类分类器有助于缩小细类分类器的候选范围，而细类分类器提供了描述每个粗类的多个属性，并可以对粗类分类器进行正则化。这种设计利用了精细类之间的关系以及精细类和粗糙类之间的关系，从而减轻了“多类”挑战带来的困难。据我们所知，我们是第一个成功训练多输出模型的人，该模型利用现有的类层次结构来改进少样本学习和监督学习。它不同于相关工作中讨论的那些使用潜在聚类层次结构而不是我们使用的显式类层次结构的方法。在表1中，我们简要比较了MahiNet与其他流行模型在学习场景方面的优势。

To address the “few-shot” problem, we apply two types of classifiers in MahiNet, i.e., MLP classifier and KNN classifier, which respectively have advantages in many-shot and few-shot situations. In principle, we always use MLP for coarse classification, and KNN for fine classification. Specially, with a sufficient amount of data in supervised learning, MLP is combined with KNN for fine classification;and in meta-learning when less data is available, we also use KNN for coarse classification to assist MLP.

为了解决“少样本”问题，我们在MahiNet中应用了两种分类器，即MLP分类器和KNN分类器，它们分别在多样本和少样本情况下具有优势。原则上，我们总是使用MLP进行粗分类，使用KNN进行精细分类。特别地，在有监督学习中，在有足够数据量的情况下，MLP与KNN相结合进行精细分类；在元学习中，当可用数据较少时，我们还使用KNN进行粗分类，以辅助MLP。

To make the KNN learnable and adaptive to new classes with few-shot data, we train an attention module to provide the similarity/distance metric used in KNN, and a rewritable memory of limited size to store and update the KNN support set during training. In supervised learning, it is necessary to maintain and update a relatively small memory (e.g., 7.2 percent of the dataset in our experiment) by selecting a few representative samples, because conducting a KNN search over all available training samples is too expensive in computation. In meta-learning, the attention module can be treated as a meta-learner that learns a universal similarity metric across different tasks.

为了使KNN能够学习并适应具有少量样本数据的新类，我们训练了一个注意力模块，以提供KNN中使用的相似性/距离度量，以及一个有限大小的可重写内存，用于在训练期间存储和更新KNN支持集。在监督学习中，有必要通过选择几个代表性样本来维护和更新相对较小的内存（例如，在我们的实验中，数据集的7.2%），因为对所有可用的训练样本进行KNN搜索的计算成本太高。在元学习中，注意力模块可以被视为元学习者，在不同的任务中学习通用的相似性度量。

Since the commonly used datasets in meta-learning do not have hierarchical multi-label annotations, we randomly extract a large subset of ImageNet [10] “mcfsImageNet” as a benchmark dataset specifically designed for MCFS problem. Each sample in mcfsImageNet has two labels: a coarse class label and a fine class label. It contains 139,346 images from 77 non-overlapping coarse classes composed of 754 randomly sampled fine classes, each has only ≈ 180 images, which might be further splitted for training, validation and test. The imbalance between different classes in the original ImageNet are preserved to reflect the imbalance in practical problems. Similarly, we further extract “mcfsOmniglot” from Omniglot [11] for the same purpose. We will make them publicly available later. In fully supervised learning experiments on these two datasets, MahiNet outperforms the widely used ResNet [1] (for fairness, MahiNet uses the same network (i.e., ResNet) as its backbone network). In meta-learning scenario where each test task covers many classes, it shows more promising performance than popular few-shot methods including prototypical networks [8] and relation networks [12], which are specifically designed for few-shot learning.

由于元学习中常用的数据集没有层次化的多标签注释，我们随机抽取ImageNet[10]中的一大个子集“mcfsImageNet”，作为专门为MCFS问题设计的基准数据集。mcfsImageNet中的每个样本都有两个标签：粗类标签和细类标签。它包含来自77个非重叠粗类的139346张图像，这些粗类由754个随机采样的细类组成，每个细类只有约180张图片，这些图片可能会被进一步分割用于训练、验证和测试。保留了原始ImageNet中不同类之间的不平衡，以反映实际问题中的不平衡。同样，出于同样的目的，我们进一步从Omniglot[11]中选取“mcfsOmniglot”。我们将在稍后公开这些信息。在这两个数据集上的完全监督学习实验中，MahiNet的表现优于广泛使用的ResNet[1]（为了公平起见，MahiNet使用与其主干网络相同的网络（即ResNet）。在元学习场景中，每个测试任务覆盖多个类，它比流行的少样本方法（包括原型网络[8]和关系网络[12]）表现出更具前景的性能，这些方法是专门为少样本学习设计的。

Our contributions can be concluded as: In the new version, we conclude our contributions at the end of introduction as follows: Our contributions can be concluded as: 1) We address a new problem setting called “many-class few-shot learning (MCFS)” that has been widely encountered in practice. Compared to the conventional “few-class few-shot (as in most few-shot learning methods)” or “many-class manyshot (as in most supervised learning methods)” settings, MCFS is more practical and challenging but has been rarely studied in the ML community. 2) To alleviate the challenge of “many-class few-shot”, we propose to utilize the knowledge of a predefined class hierarchy to train a model that takes the relationship between classes into account when generating a classifier over a relatively large number of classes.  3) To empirically justify whether our model can improve the MCFS problem by using class hierarchy information, we extract two new datasets from existing benchmarks, each coupled with a class hierarchy on reasonably specified classes. In experiments, we show that our method outperforms the other baselines in MCFS setting.

我们的贡献可以总结为：在新版本中，我们在导言末尾总结如下：1）我们解决了一个新的问题设置，称为“多类别少样本学习（MCFS）”，在实践中广泛遇到。与传统的“少类少样本（如大多数少样本学习方法）”或“多类多样本（如大多数有监督的学习方法）”设置相比，MCFS更实用、更具挑战性，但很少在ML领域进行研究。2） 为了缓解“多类少样本”的挑战，我们建议利用预定义类层次结构的知识来训练一个模型，该模型在对相对大量的类生成分类器时考虑类之间的关系。3） 为了从经验上证明我们的模型是否可以通过使用类层次结构信息来改善MCFS问题，我们从现有基准中提取了两个新的数据集，每个数据集都与合理指定的类上的类层次结构相结合。实验表明，在MCFS设置下，我们的方法优于其他基线。

2相关工作

2.1 Few-Shot Learning

Generative models [13] were trained to provide a global prior knowledge for solving the one-shot learning problem. With the advent of deep learning techniques, some recent approaches [14], [15] use generative models to encode specific prior knowledge, such as strokes and patches. More recently, works in [9] and [16] have applied hallucinations to training images and to generate more training samples, which converts a few-shot problem to a many-shot problem.

生成模型[13]经过训练，为解决单样本问题提供了全局先验知识。随着深度学习技术的出现，最近的一些方法[14]、[15]使用生成模型来编码特定的先验知识，例如笔划和面片。最近，[9]和[16]中的工作将幻觉应用于训练图像，并生成更多训练样本，从而将少样本问题转化为多样本问题。 

Meta-learning has been widely studied to address the fewshot learning problems for fast adaptation to new tasks with only few-shot data. Meta-learning was first proposed in the last century [17], [18], and has recently brought significant improvements to few-shot learning, continual learning and online learning [19]. For example, the authors of [20] proposed a dataset of characters “Omniglot” for meta-learning while the work in [21] apply a Siamese network to this dataset. A more challenging dataset “miniImageNet” [5], [7] was introduced later. miniImageNet is a subset of ImageNet [10] and has more variety and higher recognition difficulty compared to Omniglot. Researchers have also studied a combination of RNN and attention based method to overcome the few-shot problem [5]. More recently, the method in [8] was proposed based on metric learning to learn a shared KNN [22] classifier for different tasks. In contrast, the authors of [6] developed their approach based on the second order optimization where the model can adapt quickly to new tasks or classes from an initialization shared by all tasks. The work in [23] addresses the few-shot image recognition problem by temporal convolution, which sequentially encodes the samples in a task. More recently, meta-learning strategy has been studied to solve other problems and tasks, such as using meta-learning training strategy to help design a more efficient unsupervised learning rule [24]; mitigating the low-resource problems in neural machine translation task [25]; alleviating the few annotations problem in object detection problem [26]

元学习已被广泛研究，以解决少样本学习问题，快速适应新任务，只有很少的样本数据。元学习最早是在上个世纪[17]，[18]提出的，最近它给少样本学习、持续学习和在线学习带来了显著的改进[19]。例如，[20]的作者提出了一个用于元学习的字符“Omniglot”数据集，而[21]的工作将暹罗网络应用于该数据集。后来引入了一个更具挑战性的数据集“miniImageNet”[5]，[7]。miniImageNet是ImageNet[10]的一个子集，与Omniglot相比，miniImageNet具有更多种类和更高的识别难度。研究人员还研究了RNN和基于注意力的方法的结合，以克服少样本问题[5]。最近，文献[8]中的方法是基于度量学习提出的，用于学习不同任务的共享KNN[22]分类器。相比之下，[6]的作者基于二阶优化开发了他们的方法，模型可以快速适应所有任务共享的初始化中的新任务或类。[23]中的工作通过时间卷积来解决少样本图像识别问题，时间卷积在任务中对样本进行顺序编码。最近，元学习策略被研究用来解决其他问题和任务，例如使用元学习训练策略来帮助设计更有效的无监督学习规则[24]；减轻神经机器翻译任务中的低资源问题〔25〕；缓解目标检测问题中的少量注释问题[26]

Our model is closely related to prototypical networks, in which every class is represented by a prototype that averages the embedding of all samples from that class, and the embedding is achieved by applying a shared encoder, i.e., the meta-learner. It can be modified to generate an adaptive number of prototypes [27] and to handle extra weaklysupervised labels [28], [29] on a category graph. Unlike these few-shot learning methods that produces a KNN classifier defined by the prototypes, our model produces multilabels or multi-output predictions by combining the outputs of an MLP classifier and a KNN classifier, which are trained in either supervised learning or few-shot learning settings.

我们的模型与原型网络密切相关，其中每个类都由一个原型表示，该原型平均了该类中所有样本的嵌入，而嵌入是通过应用共享编码器（即元学习器）实现的。可以对其进行修改，以生成自适应数量的原型[27]，并在类别图上处理额外的弱监督标签[28]、[29]。与这些产生由原型定义的KNN分类器的少样本学习方法不同，我们的模型通过组合MLP分类器和KNN分类器的输出来产生多标签或多输出预测，后者在监督学习或少样本学习设置中训练。

2.2 Multi-Label Classification

Multi-label classification aims to assign multiple class labels to every sample [30]. One solution is to use a chain of classifiers to turn multi-label problem into several binary classification problems [31], [32], [33]. Another solution treats multi-label classification as multi-class classification over all possible subsets of labels [34]. Other works learn an embedding or encoding space using metric learning approaches [35], feature-aware label space encoding, label propagation, etc. The work in [36] proposes a decision trees method for multi-label annotation problems. The efficiency can be improved by using an ensemble of a pruned set of labels [37]. The applications include multi-label classification for textual data [38], multi-label learning from crowds [39] and disease resistance prediction [40]. Our approach differs from these works in that the multi-output labels and predictions serve as auxiliary information to improve the manyclass few-shot classification over fine classes.

多标签分类旨在为每个样本分配多个类别标签[30]。一种解决方案是使用一系列分类器将多标签问题转化为几个二进制分类问题[31]、[32]、[33]。另一种解决方案将多标签分类视为所有可能的标签子集上的多类分类[34]。其他工作使用度量学习方法[35]、特征感知标签空间编码、标签传播等学习嵌入或编码空间。在[36]中的工作提出了一种多标签注释问题的决策树方法。通过使用一组经过修剪的标签，可以提高效率[37]。这些应用包括文本数据的多标签分类[38]、人群的多标签学习[39]和抗病性预测[40]。我们的方法与这些工作的不同之处在于，多输出标签和预测可以作为辅助信息，在精细分类上改进多类少样本分类。

2.3 Hierarchical Classification

Hierarchical classification is a special case of multi-label or multi-output problems [41], [42]. It has been applied to traditional supervised learning tasks [43], such as text classification [44], [45], community data [46], case-based reasoning [47], popularity prediction [48], supergraph search in graph databases [49], road networks [50], image annotation and robot navigation. However, to the best of our knowledge, our paper is the first work successfully leveraging class hierarchy information in few-shot learning and meta-learning tasks. Previous methods such as [51], have considered the class hierarchy information but failed to achieve improvement and thus did not integrate it in their method, whereas our method successfully leverage the hierarchical relationship between classes to improve the classification performance by using a memory-augmented model.

分层分类是多标签或多输出问题的特例[41]，[42]。它已被应用于传统的有监督学习任务[43]，如文本分类[44]、[45]、社区数据[46]、基于案例的推理[47]、人气预测[48]、图形数据库中的超图搜索[49]、道路网络[50]、图像注释和机器人导航。然而，据我们所知，我们的论文是第一个成功地在少样本学习和元学习任务中利用类层次信息的工作。以前的方法（如[51]）考虑了类的层次结构信息，但未能实现改进，因此没有将其集成到方法中，而我们的方法成功地利用类之间的层次关系，通过使用内存增强模型来提高分类性能。

Similar idea of using hierarchy for few-shot learning has been studied in [52], [53], which learns to cluster semantic information and task representation, respectively. [28]  tilizes coarsely labeled data in the hierarchy as weakly supervised data rather than multi-label annotations for few-shot learning. In computational biology, hierarchy information has also been found helpful in gene function prediction, where two main taxonomies are Gene Ontology and Functional Catalogue. [54] proposed a truth path rule as an ensemble method to govern both taxonomies. [55] shows that the key factors for the success of hierarchical ensemble methods are: (1)the integration and synergy among multilabel hierarchy, (2) data fusion, (3) cost-sensitive approaches, and (4) the strategy of selecting negative examples. [56] and [57] address the incomplete annotations of proteins using label hierarchy (as studied in this paper) by following the idea of few-shot learning. Specifically, they learn to predict the new gene ontology annotations by Bi-random walks on a hybrid graph [56] and downward random walks on a gene ontology [57], respectively.

[52]、[53]中也研究了使用层次结构进行少样本学习的类似想法，这两种学习分别对语义信息和任务表示进行聚类。[28]将层次结构中粗略标记的数据平铺为弱监督数据，而不是用于少样本学习的多标签注释。在计算生物学中，层次信息也被发现有助于基因功能预测，其中两个主要分类是基因本体和功能目录。[54]提出了一个真理路径规则，作为管理这两种分类法的集成方法。[55]表明，层次集成方法成功的关键因素是：（1）多标签层次之间的集成和协同（2）数据融合（3）成本敏感的方法（4）选择负面示例的策略。[56]和[57]通过遵循少样本学习的思想，使用标签层次结构（如本文所研究的）解决了蛋白质的不完整注释。具体来说，他们分别通过混合图[56]上的双随机游动和基因本体[57]上的向下随机游动来学习预测新的基因本体注释。

3 针对性问题和提出的模型

In this section, we first introduce the formulation of manyclass few-shot problem in Section 3.1. Then we generally elaborate our network architecture in Section 3.2. Details for how to learn a similarity metric for a KNN classifier with attention module and how to update the memory (as a support set of the KNN classifier) are given in Sections 3.3 and 3.4 respectively.

在本节中，我们首先在第3.1节中介绍多类少样本问题的公式。然后，我们将在第3.2节中详细阐述我们的网络架构。第3.3节和第3.4节分别给出了如何学习带有注意模块的KNN分类器的相似性度量以及如何更新内存（作为KNN分类器的支持集）的详细信息。

3.1 Problem Formulation

We study supervised learning and meta-learning. Given a training set of n samples , where each sample xi ∈ X is associated with multiple labels. For simplicity, we assume that each training sample is associated with two labels: a fine-class label yi ∈ Y and a coarse-class label zi ∈ Z. The training data is sampled from a data set D, i.e., （xi，yi，zi）~ D. Here, X denotes the set of samples; Y denotes the set of all the fine classes, and Z denotes the set of all the coarse classes. To define a class hierarchy for Y and Z, we further assume that each coarse class z ∈ Z covers a subset of fine classes Yz, and that distinct coarse classes are associated with disjoint subsets of fine classes, i.e., for any z1， z2 ∈ Z, we have Yz1 ∩ Yz2 =φ. Our goal is fine-class classification by using the class hierarchy information and the coarse labels of the training data. In particular, the supervised learning setting in this case can be formulated as:

我们研究监督学习和元学习。给定一组n个样本的训练集，其中每个样本xi∈ X与多个标签关联。为了简单起见，我们假设每个训练样本都与两个标签相关联：一个精细类标签yi∈ Y和一个粗糙的类标签zi∈Z. 训练数据从数据集D中取样,（xi，yi，zi）~ D。这里，X表示样本集合；Y表示所有精细类的集合，Z表示所有粗糙类的集合。为了定义Y和Z的类层次结构，我们进一步假设每个粗略的类z ∈ Z覆盖了细类Yz的子集，不同的粗类与细类的不相交子集相关联，即，对于任何z1，z2∈ Z、 我们有Yz1∩ Yz2=φ。我们的目标是利用类层次信息和训练数据的粗略标签进行精细分类。具体而言，这种情况下的监督学习设置可以表示为：                 

 

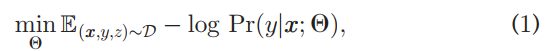
where Ѳ is the model parameters and E refers to the expectation w.r.t. the data distribution. In practice, we solve the corresponding empirical risk minimization (ERM) during training, i.e.,

其中Ѳ是模型参数，E是数据分布的期望。在实践中，我们在训练期间解决了相应的经验风险最小化（ERM）：  

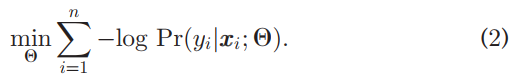
In contrast, meta-learning aims to learn a meta-learner model that can be applied to different tasks. Its objective is to maximize the expectation of the prediction likelihood of a task drawn from a distribution of tasks. Specifically, we assume that each task is the classification over a subset of fine classes T sampled from a distribution T over all classes, and the problem is formulated as

相比之下，元学习旨在学习一种可以应用于不同任务的元学习者模型。其目标是最大化从任务分布中得出的任务预测可能性的期望。具体地说，我们假设每个任务都是从所有类的分布T中采样的精细类T子集上的分类，问题的形式如下：

where DT refers to the set of samples with label yi ∈ T. The corresponding ERM is

式中，DT指标签为yi的样本集∈T。相应的ERM为 

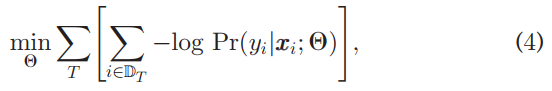
where T represents a task (defined by a subset of fine classes) sampled from distribution T , and DT is a training set for task T sampled from DT.

其中，T表示从分布T中采样的任务（由精细类的子集定义），DT是从DT中采样的任务T的训练集。

To leverage the coarse class information of Z, we write in Eqs. (1) and (3) as

为了利用Z的粗类信息，我们编写了等式。（1）和（3）如下：

where Ѳf and Ѳc are the model parameters for fine classifier and coarse classifier, respectively.Accordingly, given a specific sample (xi; yi, zi) with its ground truth labels for coarse and fine classes, we can write in Eqs. (2) and (4) as follows.

式中，Ѳf和Ѳc分别是细分类器和粗分类器的模型参数。相应地，给定一个特定样本（xi；yi，zi）及其粗类和细类的基本真值标签，我们可以在等式中写出。（2） 和（4）如下：

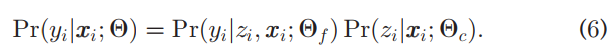
Suppose that a DNN model already produces a logit ay for each fine class y, and a logit bz for each coarse class z, the two probabilities in the right hand side of Eq. (6) are computed by applying softmax function to the logit values in the following way. 

假设DNN模型已经为每个细类y生成了一个logit ay，为每个粗类z生成了一个logit bz，则等式（6）右侧的两个概率是通过以下方式将softmax函数应用于logit值来计算的。 

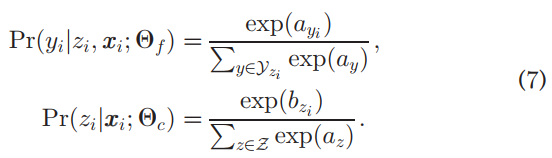
Therefore, we integrate multiple labels (both the fineclass label and coarse-class label) in an ERM, whose goal is to maximize the likelihood of the ground truth fine-class label. Given a DNN that produces two vectors of logits a and b for fine class and coarse class respectively, we can train the DNN for supervised learning or meta-learning by solving the ERM problems in Eqs. (2) or (4) (with Eqs. (6) and (7) plugged in).

因此，我们在一个ERM中集成了多个标签（精细类标签和粗糙类标签），其目标是最大限度地提高基础真值精细类标签的可能性。给定一个DNN，它分别为精细类和粗糙类生成两个logits a和b向量，我们可以通过解决等式中的ERM问题来训练DNN进行监督学习或元学习。（2） 或（4）（插入等式（6）和（7））。 

3.2 Network Architecture

To address MCFS problem in both supervised learning and meta-learning scenarios, we developed a universal model, MahiNet, as in Fig. 2. MahiNet uses a CNN to extract features from raw inputs, and then applies two modules to produce coarse-class prediction and fine-class prediction, respectively. Each module includes one or two classifiers: either an MLP or an attention-based KNN classifier or both. Intuitively, MLP performs better when data is sufficient, while the KNN classifier is more stable in few-shot scenario. Hence, we always apply MLP to coarse prediction and always apply KNN to fine prediction. In addition, we use KNN to assist MLP for the coarse module in meta-learning, and use MLP to assist KNN for the fine module in supervised learning. We develop two mechanisms to make the KNN classifier learnable and be able to quickly adapt to new tasks in the meta-learning scenario. In the attention-based KNN classifier, an attention module is trained to compute the similarity between two samples, and a rewritable memory is maintained with a highly epresentative support set for KNN prediction. The memory is updated during training

为了解决监督学习和元学习场景中的MCFS问题，我们开发了一个通用模型MahiNet，如图2所示。MahiNet使用CNN从原始输入中提取特征，然后应用两个模块分别生成粗类预测和细类预测。每个模块包括一个或两个分类器：MLP或基于注意的KNN分类器，或两者兼而有之。直观地说，当数据足够时，MLP性能更好，而KNN分类器在少样本场景中更稳定。因此，我们总是将MLP应用于粗预测，将KNN应用于细预测。此外，在元学习中，我们使用KNN来辅助粗糙模块的MLP，在监督学习中使用MLP来辅助精细模块的KNN。我们开发了两种机制，使KNN分类器可学习，并能够快速适应元学习场景中的新任务。在基于注意的KNN分类器中，训练一个注意模块来计算两个样本之间的相似性，并使用具有高度代表性的KNN预测支持集来维持可重写记忆。记忆会在训练期间更新。

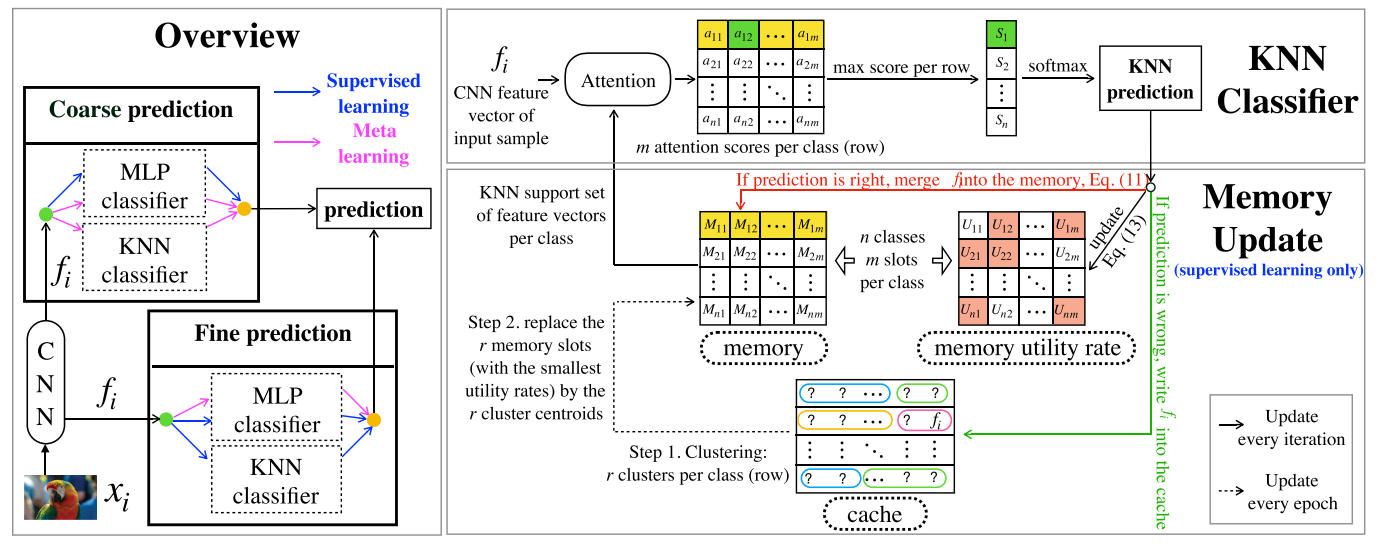
Fig. 2. Left: MahiNet. The final fine-class prediction combines predictions based on multiple classes (both fine classes and coarse classes), each of which is produced by an MLP classifier or/and an attention-based KNN classifier. Top right: KNN classifier with learnable similarity metric and updatable support set. Attention provides a similarity metric aj,k between each input sample fi and a small support set per class stored in memory Mj,k. The learning of KNN classifier aims to optimize 1) the similarity metric parameterized by the attention, detailed in Section 3.3; and 2) a small support set of feature vectors per class stored in memory, detailed in Section 3.4. Bottom right: The memory update mechanism. In meta-learning, the memory stores the features of all training samples of a task. In supervised learning, the memory is updated during training as follows: for each sample xi within an epoch, if the KNN classifier produces correct prediction, fi will be merged into the memory; otherwise, fi will be written into a “cache”. At the end of each epoch, we apply clustering to the samples per class stored in the cache, and use the resultant centroids to replace r slots of the memory with the smallest utility rate [58].

左：MahiNet。最终的精细类预测结合了基于多个类（精细类和粗糙类）的预测，每个类都由MLP分类器或/和基于注意的KNN分类器生成。右上：具有可学习相似性度量和可更新支持集的KNN分类器。注意在每个输入样本fi和存储在内存Mj,|k中的每个类的一个小支持集之间提供一个相似性度量aj,k。KNN分类器的学习旨在优化1）注意参数化的相似性度量，详见第3.3节；2）存储在内存中的每个类的特征向量的小支持集，详见第3.4节。右下：内存更新机制。在元学习中，记忆存储任务的所有训练样本的特征。在监督学习中，在训练期间更新存储器：对于每个样本Xi在一个时期内，如果KNN分类器产生正确的预测，fi将合并到存储器中；否则，fi将被写入“缓存”。在每个epoch结束时，我们对缓存中存储的每个类的样本进行聚类，并使用生成的质心以最小的利用率替换内存中的r个slots[58]。

Our method for learning a KNN classifier combines the ideas from two popular meta-learning methods, i.e., matching networks [7] that aim to learn a similarity metric, and prototypical networks [8] that aim to find a representative center per class for NN search. However, our method relies on an augmented memory rather than a bidirectional RNN for retrieving of NN in matching networks. In contrast to prototypical networks, which only has one prototype per class, we allow multiple prototypes as long as they can fit in the memory budget. Together these two mechanisms prevent the confusion caused by subtle differences between classes in “manyclass” scenario. Notably, MahiNet can also be extended to “life-long learning” given this memory updating mechanism. We do not adopt the architecture used in [23] since it requires the representations of all historical data to be stored.

我们学习KNN分类器的方法结合了两种流行元学习方法的思想，即旨在学习相似性度量的匹配网络[7]和旨在为NN搜索找到每个类的代表中心的原型网络[8]。然而，我们的方法依赖于扩充内存而不是双向RNN来检索匹配网络中的NN。与每个类只有一个原型的原型网络不同，我们允许多个原型，只要它们能满足内存预算。这两种机制共同防止了“manyclass”场景中类之间的细微差异造成的混淆。值得注意的是，考虑到这种记忆更新机制，MahiNet还可以扩展到“终身学习”。我们不采用[23]中使用的架构，因为它要求存储所有历史数据的表示。 

3.3 Learn a KNN Similarity Metric With an Attention

In MahiNet, we train an attention module to compute the similarity used in the KNN classifier. The attention module learns a distance metric between the feature vector fi of a given sample xi and any feature vector from the support set stored in the memory. Specifically, we use the dot product attention similar to the one adopted in [59] for supervised learning, and use an euclidean distance based attention for meta-learning, following the instruction from [8]. Given a sample xi, we compute a feature vector fi ∈ Rd by applying a backbone CNN to xi. In the memory, we maintain a support set of m feature vectors for each class, i.e., M∈ Rc*m*d, where C is the number of classes. The KNN classifier produces the class probabilities of xi by first calculating the attention scores between fi and each feature vector in the memory, as follows.

在MahiNet中，我们训练一个注意力模块来计算KNN分类器中使用的相似性。注意力模块学习给定样本xi的特征向量fi与存储在存储器中的支持集的任何特征向量之间的距离度量。具体而言，我们使用与[59]中所采用的有监督学习类似的点积注意，并按照[8]中的说明，使用基于欧几里德距离的注意进行元学习。给定样本xi,我们计算特征向量fi ∈ Rd通过将CNN应用于xi。在内存中，我们为每个类维护一个由m个特征向量组成的支持集，即M∈ Rc*m*d，其中C是类数。KNN分类器通过首先计算存储器中的fi和每个特征向量之间的关注分数来产生xi的类概率，如下所示

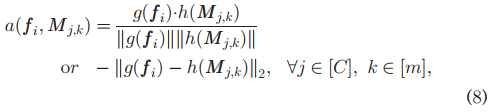
where g and h are learnable transformations for fi and the feature vectors in the memory.

其中g和h是fi和存储器中的特征向量的可学习变换。

We select the top K nearest neighbors, denoted by top K, of fi among the m feature vectors for each class j, and compute the sum of their similarity scores as the attention score of fi to class j, i.e., 

我们在每个类j的m个特征向量中选择fi的前K个最近邻，用top K表示，并计算它们的相似性分数之和作为fi对类j的注意分数，即：

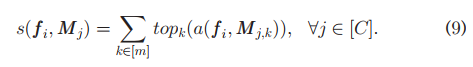
We usually find K = 1 is sufficient in practice. The predicted class probability is derived by applying a softmax function to the attention scores of fi over all C classes, i.e.,

我们通常发现K=1在实践中是足够的。通过对所有C类的fi注意分数应用softmax函数，得出预测的类概率，即：

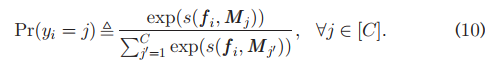
3.4 Memory Mechanism for the Support Set of KNN

Ideally, the memory M ∈ Rc*m*d can store all available training samples as the support set of the KNN classifier. In meta-learning, in each episode, we sample a task with C classes and m training samples per class, and store them in the memory. Due to the small amount of training data for each task, we can store all of them and thus do not need to update the memory. In supervised learning, we only focus on one task. This task usually has a large training set and it is inefficient, unnecessary and too computationally expensive to store all the training set in the memory. Hence, we set up a budget hyper-parameter m for each class. m is the maximal number of feature vectors to be stored in the memory for one class. Moreover, we develop a memory update mechanism to maintain a small memory with diverse and representative feature vectors per class (t-SNE visualization of the diversity and representability of the memory can be found in the experiment section.). Intuitively, it can choose to forget or merge feature vectors that are no longer representative, and select new important feature vectors into memory.

理想情况下，内存∈ Rc*m*d可以将所有可用的训练样本存储为KNN分类器的支持集。在元学习中，在每一集中，我们用C类和每类m个训练样本对一个任务进行采样，并将它们存储在内存中。由于每个任务的训练数据量很小，我们可以存储所有数据，因此不需要更新内存。在监督学习中，我们只关注一项任务。这个任务通常有一个大的训练集，而且将所有的训练集存储在内存中效率低、不必要，而且计算成本太高。因此，我们为每个类设置了一个预算超参数m。m是存储在一个类的内存中的最大特征向量数。此外，我们还开发了一种内存更新机制，以维护每类具有多样性和代表性特征向量的小型内存（可以在实验部分找到内存多样性和代表性的t-SNE可视化）。直观地说，它可以选择忘记或合并不再具有代表性的特征向量，并将新的重要特征向量选择到内存中。

We will show later in experiments that a small memory can result in sufficient improvement, while the time cost of memory updating is negligible. Accordingly, the memory in meta-learning does not need to be updated according to a rule, while in supervised learning, we design the writing rule as follows. During training, for the data that can be correctly predicted by the KNN classifier, we merge its feature with corresponding slots in the memory by computing their convex combination, i.e.

我们将在稍后的实验中展示，一个小的内存可以带来足够的改善，而内存更新的时间成本可以忽略不计。因此，元学习中的记忆不需要根据规则进行更新，而在监督学习中，我们设计了如下的书写规则。在训练过程中，对于KNN分类器能够正确预测的数据，我们通过计算它们的凸组合，将其特征与内存中相应的槽合并，即， 

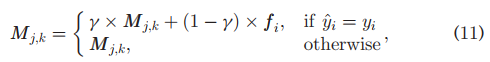
where yi is the ground truth label, and γ=0.95 is a combination weight that works well in most of our empirical studies; for input feature vector that cannot be correctly predicted, we write it to a cache C ={C1,..., Cc} that stores the candidates written into the memory for the next epoch, i.e.,

其中，yi是基本真值标签，γ=0.95是一个组合权重，在我们的大多数实证研究中效果良好；对于无法正确预测的输入特征向量，我们将其写入缓存C={C1，…，Cc}，该缓存将写入下一个epoch的候选项存储在内存中，即

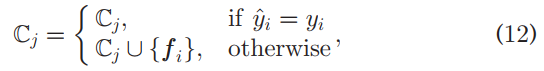
Concurrently, we record the utility rate of the feature vectors in the memory, i.e., how many times each feature vector being selected into the K nearest neighbor during the epoch. The rates are stored in a matrix U ∈ Rc*m, and we update it as follows.

同时，我们在内存中记录特征向量的利用率，即在epoch期间，每个特征向量被选择到K个最近邻中的次数。速率存储在矩阵U中∈ Rc*m，我们更新如下

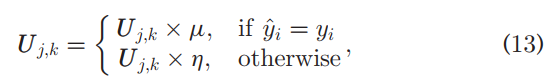
 where m ∈（1,2）and h ∈（0,1） are hyper-parameters.      m和h是超参数

At the end of each epoch, we apply clustering to the feature vectors per class in the cache, and obtain r cluster centroids as the candidates for memory update in the next epoch. Then, for each class, we replace r feature vectors in the memory that have the smallest utility rate with the r cluster centroids. 

在每个epoch结束时，我们对缓存中每个类的特征向量进行聚类，并获得r个聚类质心作为下一个历元内存更新的候选。然后，对于每个类，我们用r簇质心替换内存中效用率最小的r个特征向量。 

 4 训练策略

As shown in the network structure in Fig. 2, in supervised learning and meta-learning, we use different combinations of MLP and KNN to produce the multi-output predictions of fine-class and coarse-class. The classifiers are combined by summing up their output logits for each class, and a softmax function is applied to the combined logits to generate the class probabilities. Assume the MLP classifiers for the coarse classes and the fine classes are, the KNN classifiers for the coarse classes and the fine classes are. In supervised learning, the model parameters are ; in meta-learning setting, the model parameters are .

如图2的网络结构所示，在监督学习和元学习中，我们使用MLP和KNN的不同组合来产生精细类和粗类的多输出预测。通过对每个类的输出logit求和来组合分类器，并对组合的logit应用softmax函数来生成类概率。假设粗类和细类的MLP分类器为，粗类和细类的KNN分类器为。在监督学习中，模型参数为；在元学习环境下，模型参数为。

According to Section 3.1, we train MahiNet for supervised learning by solving the ERM problem in Eq. (2). For meta-learning, we instead train MahiNet by solving Eq. (4). As previously mentioned, the multi-output logits (for either fine classes or coarse classes) used in those ERM problems are obtained by summing up the logits produced by the corresponding combination of the classifiers.

根据第3.1节，我们通过解决等式（2）中的ERM问题来训练MahiNet进行监督学习。对于元学习，我们通过解决等式（4）来训练MahiNet。如前所述，在这些ERM问题中使用的多输出Logit（针对精细类或粗糙类）是通过将分类器的相应组合产生的Logit相加得到的。

4.1 Training MahiNet for Supervised learning

In supervised learning, the memory update relies heavily on the clustering of the merged feature vectors in the cache. To achieve relatively high-quality feature vectors, we first pretrain the CNN+MLP model by using standard backpropagation, which minimizes the sum of cross entropy loss on both the coarse-classes and fine-classes. The loss is computed based on the logits of fine-classes and the logits of coarse-classes, which are the outputs of the corresponding MLP classifiers. Then, we fint-tune the whole model, which includes the fineclass KNN classifier, with memory update applied. Specifically, in every iteration, we first update the parameters of the model with mini-batch SGD based on the coarse-level and fine-level logits produced by the MLP and KNN classifiers. Then, the memory that stores a limited number of representative feature maps for every class is updated by the rules explained in Section 3.4, as well as the associated utility rates and feature cache. The details of the training procedure during the fine-tune stage is explained in Algorithm 1.

在有监督学习中，记忆更新在很大程度上依赖于缓存中合并特征向量的聚类。为了获得相对高质量的特征向量，我们首先使用标准的反向传播对CNN+MLP模型进行预训练，这样可以最小化粗类和细类的交叉熵损失之和。损失是基于细类的logit和粗类的logit计算的，这是相应的MLP分类器的输出。然后，我们找到了整个模型，其中包括fineclass KNN分类器，并应用了内存更新。具体地说，在每次迭代中，我们首先根据MLP和KNN分类器产生的粗层和细层Logit，使用小批量SGD更新模型的参数。然后，根据第3.4节中解释的规则以及相关的实用率和功能缓存，为每个类别存储有限数量的代表性功能图的内存将被更新。算法1解释了微调阶段的训练过程细节。

 

 4.2 Training MahiNet for Meta-Learning

When sampling the training/test tasks, we allow unseen fine classes that were not covered in any training task to appear in test tasks, but we fix the ground set of the coarse classes for both training and test tasks. Hence, every coarse class appearing in any test task has been seen during training, but the corresponding fine classes belonging to this coarse class in training and test tasks can be vary.

在对训练/测试任务进行采样时，我们允许在测试任务中出现未包含在任何训练任务中的看不见的精细类，但我们为训练和测试任务修复了粗糙类的基础集。因此，在训练过程中，任何测试任务中出现的每一个粗糙类都是可见的，但在训练和测试任务中属于这个粗糙类的相应精细类可能会有所不同。

In the meta-learning setting, since the tasks in different iterations targets samples from different subsets of classes and thus ideally need different feature map representations [60], we do not maintain the memory during training so every class can have a fixed representation. Instead, the memory is only maintained within each iteration for a specific task and it stores feature map representations extracted from the support set of the task. The detailed training procedure can be found in Algorithm 2. In summary, we generate a training task by randomly sampling a subset of fine classes, and then we randomly sample a support set S and a query set Q from the associated samples belonging to these classes. We store the CNN feature vectors of S in the memory, and train MahiNet to produce correct  redictions for the samples in Q with the help of coarse label predictions. 

在元学习环境中，由于不同迭代中的任务以来自不同类别子集的样本为目标，因此理想情况下需要不同的特征图表示[60]，因此我们在训练期间不会保持记忆，因此每个类别都可以有固定的表示。相反，内存仅在特定任务的每次迭代中维护，并存储从任务支持集提取的特征地图表示。详细的训练过程可以在算法2中找到。总之，我们通过随机抽样一个子集的精细类来生成一个训练任务，然后从属于这些类的相关样本中随机抽样一个支持集S和一个查询集Q。我们将S的CNN特征向量存储在内存中，并训练MahiNet在粗糙标签预测的帮助下对Q中的样本产生正确的预测。

5 实验

In this section, we first introduce two new benchmark datasets specifically designed for MCFS problem, and compare them with other popular datasets in Section 5.1. Then, we show that MahiNet has better generality and can outperform the specially designed models in both supervised learning (in Section 5.2) and meta-learning (in Section 5.3) scenarios. We also present an ablation study of MahiNet to show the improvements brought by different components and how they interact with each other. In Section 5.4, we report the comparison with the variants of baseline models in order to show the broad applicability of our strategy of leveraging the hierarchy structures. In Section 5.6, we present an analysis of the computational costs caused by the augmented memory in MahiNet.

在本节中，我们首先介绍两个专门为MCFS问题设计的新基准数据集，并将它们与第5.1节中其他流行的数据集进行比较。然后，我们证明了MahiNet具有更好的通用性，并且在监督学习（第5.2节）和元学习（第5.3节）场景中都优于专门设计的模型。我们还介绍了MahiNet的消融研究，以展示不同组件带来的改进以及它们如何相互作用。在第5.4节中，我们报告了与基线模型变体的比较，以显示我们利用层次结构的策略的广泛适用性。在第5.6节中，我们分析了MahiNet中的扩充内存造成的计算成本。

5.1 Two New Benchmarks for MCFS Problem: mcfsImageNet & mcfsOmniglot

Since existing datasets for both supervised learning and meta-learning settings neither support multiple labels nor fulfill the requirement of “many-class few-shot” settings, we propose two novel benchmark datasets specifically for MCFS Problem, i.e., mcfsImageNet & mcfsOmniglot. The samples in them are annotated by multiple labels of different granularity. We compare them with several existing datasets in Table 2. Our following experimental study focuses on these two datasets. 

由于监督学习和元学习设置的现有数据集既不支持多个标签，也不满足“多类少样本”设置的要求，我们针对MCFS问题提出了两个新的基准数据集，即mcfsImageNet和mcfsOmniglot。其中的样本由多个不同粒度的标签进行注释。我们将其与表2中的几个现有数据集进行了比较。我们下面的实验研究集中在这两个数据集上。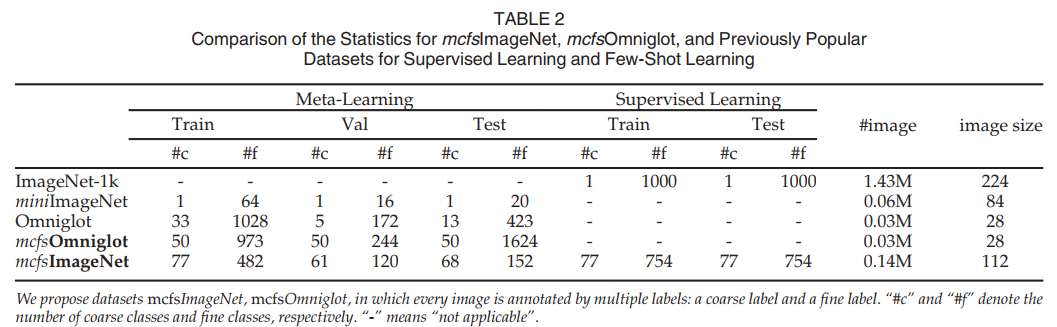 

Hence, to develop a benchmark dataset specifically for the purpose of testing the performance of MCFS learning, we extracted a subset of images from ImageNet and created a dataset called “mcfsImageNet”. Table 2 compares the statistics of mcfsImageNet with several benchmark datasets. Comparing to the original ImageNet, we avoided selecting the samples that belong to more than one coarse classes into mcfsImageNet in order to meet the class hierarchy requirements of MCFS problem, i.e., each fine class only belongs to one coarse class. Compared to miniImageNet, mcfsImageNet is about 5* larger, and covers 754 fine classes in total, which is much more than the 80 fine classes in miniImageNet. Moreover, on average, each fine class only has ~185 images for training and test, which matches the typical MCFS scenarios in practice. Additionally, the number of coarse classes in mcfsImageNet is 77, which is much less than 754 of the fine classes. This is consistent with the data properties found in many practical applications, where the coarse-class labels can only provide weak supervision, but each coarse class has sufficient training samples. Further, we avoided selecting coarse classes which are too broad or contain too many different fine classes. For example, the “Misc” class in ImageNet has 20400 sub-classes, and includes both animal (3998 subclasses) and plant (4486 sub-classes). This kind of coarse label covers too many classes and cannot provide valuable information to distinguish different fine classes.

因此，为了开发一个专门用于测试MCFS学习性能的基准数据集，我们从ImageNet中提取了一部分图像，并创建了一个名为“mcfsImageNet”的数据集。表2将mcfsImageNet的统计数据与几个基准数据集进行了比较。与原始ImageNet相比，我们避免了将属于多个粗类的样本选择到mcfsImageNet中，以满足MCFS问题的类层次要求，即每个细类只属于一个粗类。与miniImageNet相比，mcfsImageNet大约大5*个，总共覆盖754个精细类，远远超过miniImageNet中的80个精细类。此外，每个类别只有约185张训练和测试图像，这与实践中典型的MCFS场景相匹配。此外，mcfsImageNet中的粗类数量为77个，远远少于754个细类。这与许多实际应用中发现的数据属性是一致的，在这些应用中，粗类标签只能提供微弱的监督，但每个粗类都有足够的训练样本。此外，我们避免选择太宽或包含太多不同精细类的粗糙类。例如，ImageNet中的“Misc”类有20400个子类，包括动物（3998个子类）和植物（4486个子类）。这种粗糙的标签覆盖了太多的类别，无法提供有价值的信息来区分不同的精细类别。

Omniglot [11] is a small hand-written character dataset with two-level class labels. However, in their original training/test splitting, the test set contains new coarse classes that are not covered by the training set, since this weakly labeled information is not supposed to be utilized during the training stage. This is inconsistent with the MCFS settings, in which all the coarse classes are exposed in training, but new fine classes can still emerge during test. Therefore, we resplit mniglot to fulfill the MCFS problem requirement.

Omniglot[11]是一个小型手写字符数据集，具有两级类标签。然而，在最初的训练/测试拆分中，测试集包含训练集未涵盖的新粗糙类，因为在训练阶段不应该使用这种弱标记信息。这与MCFS设置不一致，在MCFS设置中，所有的粗类都在训练中暴露出来，但在测试过程中仍然可以出现新的细类。因此，我们重新分配mniglot以满足MCFS问题要求。

5.2 Supervised Learning Experiments

5.2.1 Setup
We use ResNet18 [1] as the backbone CNN. The transformation functions g and h in the attention module are two fully connected layers followed by group normalization [62] with a residual connection. We set the memory size to m = 12 and the number of clusters to r = 3, which can achieve a better trade-off between the memory cost and performance. Batch normalization [63] is applied after each convolution and before activation. During pre-training, we apply the cross entropy loss on the probability predictions in Eq. (7). During fine-tuning, we fix the uCNN, uMLP c , and uMLP f to ensure the fine-tuning process is stable. We use SGD with a mini-batch size of 128 and a cosine learning rate scheduler with an initial learning rate 0.1. m = 1.05, h = 0.95, a weight decay of 0.0001, and a momentum of 0.9 are used. We train the model for 100 epochs during pre-training and 90 epochs for the fine-tuning. All hyperparameters are tuned on 20 percent samples randomly sampled from the training set. we use 20 percent data randomly sampled from the training set to serve as the validation set to tune all the hyperparameters.

我们使用ResNet18[1]作为CNN的主干。注意模块中的转换函数g和h是两个完全连接的层，后面是带有剩余连接的组规范化[62]。我们将内存大小设置为m=12，集群数量设置为r=3，这可以在内存成本和性能之间实现更好的权衡。批量标准化[63]在每次卷积之后和激活之前应用。在预训练期间，我们将交叉熵损失应用于等式（7）中的概率预测。在微调过程中，我们修复了，以确保微调过程是稳定的。我们使用最小批量为128的SGD和初始学习率为0.1的余弦学习率调度器。m=1.05，h=0.95，重量衰减为0.0001，动量为0.9。我们在预训练期间对模型进行了100个阶段的训练，并对模型进行了90个阶段的微调。所有超参数均基于从训练集中随机抽取的20%样本进行调整。我们使用从训练集中随机抽取的20%的数据作为验证集来调整所有超参数。

 5.2.2 Experiments on mcfsImageNet

Table 3 compares MahiNet with the supervised learning model (i.e., ResNet18) and meta-learning model (i.e., prototypical networks) in the setting of supervised learning. The results show that MahiNet outperforms the specialized models, such as ResNet18 in MCFS scenario.

表3比较了MahiNet与监督学习模型（即ResNet18）和元学习模型（即原型网络）在监督学习设置中的差异。结果表明，MahiNet优于专门的模型，例如MCFS场景中的ResNet18。

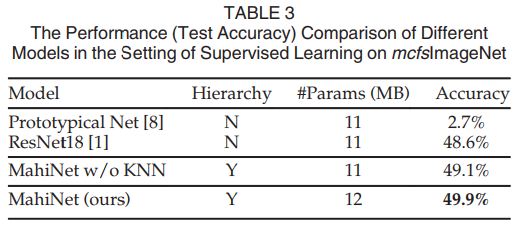
We also show the number of parameters for every method, which indicates that our model only has 9 percent more parameters than the baselines. Even using the version without KNN (which has the same number of parameters as baselines) can still outperform them.

我们还显示了每种方法的参数数量，这表明我们的模型的参数仅比基线多9%。即使使用不带KNN的版本（与基线具有相同数量的参数），其性能仍然优于它们。

Prototypical networks have been specifically designed for few-shot learning. Although it can achieve promising performance on few-shot tasks each covering only a few classes and samples, it fails when directly used to classify many classes in the classical supervised learning setting, as shown in Table 3. A primary reason, as we discussed in Section 1, is that the resulted prototype suffers from high variance (since it is simply the average over an extremely few amount of samples per class) and cannot distinguish each class from tens of thousands of other classes (few-shot learning task only needs to distinguish it from 5-10 classes). Hence, dedicated modifications is necessary to make prototypical networks also work in the supervised learning setting. One motivation of this paper is to develop a model that can be trained and directly used in both settings.

原型网络是专门为少样本学习而设计的。虽然它可以在少样本任务上取得令人满意的性能，每个任务只覆盖几个类和样本，但在经典的监督学习环境中直接用于分类许多类时，它失败了，如表3所示。正如我们在第1节中所讨论的，一个主要原因是，生成的原型存在很大的差异（因为它只是每个类极少量样本的平均值），并且无法将每个类与成千上万个其他类区分开来（少样本学习任务只需要将其与5-10个类区分开来）。因此，需要进行专门的修改，以使原型网络也能在有监督的学习环境中工作。本文的一个动机是开发一个可以在两种环境下训练和直接使用的模型。

The failure of Prototypical networks in supervised learning setting is not too surprising since for prototypical network the training and test task in the supervised setting is significantly different. We keep its training stage the same (i.e., target a task of 5 classes in every episode). In the test stage, we use the prototypes as the per-class means of training samples in each class to perform classification over all available classes on the test set data. Note the number of classes in the training tasks and the test task are significantly different, which introduces a large gap between training and test that leads to the failure. This can also be validated by observing the change on performance when we intentionally reduce the gap: the accuracy improves as the number of classes in each training task increases.

原型网络在有监督学习环境中的失败并不令人惊讶，因为对于原型网络，在有监督学习环境中的训练和测试任务是显著不同的。我们保持其训练阶段不变（即每集5节课的目标任务）。在测试阶段，我们使用原型作为每个类中训练样本的每类手段，对测试集数据上的所有可用类进行分类。请注意，训练任务和测试任务中的类别数量存在显著差异，这导致了训练和测试之间的巨大差距，从而导致失败。当我们有意缩小差距时，也可以通过观察绩效的变化来验证这一点：随着每个训练任务中的课程数量增加，准确性也会提高。

Another potential method to reduce the training-test gap is to increase the number of classes/ways per task to the same number of classes in supervised learning. However, prototypical net requires an prohibitive memory cost in such many class setting, i.e, it needs to keep 754(number of classes) * 2(1 for support set, 1 for query set)=1512 samples in memory for 1 shot learning setting and 754 * 6(5 for support set, 1 for query set) = 4536 samples for 5 shots setting. Unlike classical supervised learning models which only needs to keep the model parameters in memory, prototypical net needs to build prototypes on the fly from the fewshot samples in the current episode, so at least one sample should be available to build the prototypes and at least one sample for query.

减少训练测试差距的另一个潜在方法是，在监督学习中，将每个任务的ways增加到相同的类别数量。然而，在这样多的类设置中，原型网络需要一个极大的内存开销，即它需要在内存中保留754（类数）*2（1用于支持集，1用于查询集）=1512个样本，用于单样本学习设置，754*6（5用于支持集，1用于查询集）=4536个样本，用于5-shot设置。与经典的监督学习模型不同，原型网络只需要将模型参数保存在内存中，原型网络需要从当前事件中的fewshot 样本动态构建原型，因此至少应该有一个样本可用于构建原型，至少有一个样本可用于查询。

To separately measure the contribution of the class hierarchy and the attention-based KNN classifier, we conduct an ablation study that removes the KNN classifier from MahiNet. The results show that MahiNet still outperforms ResNet18 even when only using the extra coarse-label information and an MLP classifier for fine classes during training. Using a KNN classifier further improves the performance since KNN is more robust in the few-shot finelevel classifications. In supervised learning scenario, memory update is applied in an efficient way. 1) For each epoch, the average clustering time is 30s and is only 7.6 percent of the total epoch time (393s). 2) Within an epoch, the memory update time (0.02s) is only 9 percent of the total iteration time (0.22s).

为了分别测量类层次结构和基于注意的KNN分类器的贡献，我们进行了一项消融研究，将KNN分类器从MahiNet中移除。结果表明，即使在训练过程中仅使用超粗标签信息和MLP分类器进行精细分类，MahiNet仍优于ResNet18。使用KNN分类器进一步提高了性能，因为KNN在少数镜头精细级别分类中更具鲁棒性。在监督学习场景中，记忆更新被有效地应用。1） 对于每个epoch，平均聚类时间为30秒，仅占总历元时间（393秒）的7.6%。2） 在一个epoch内，内存更新时间（0.02s）仅为总迭代时间（0.22s）的9%。

5.3 Meta-Learning Experiments

5.3.1 Setup

We use the same backbone CNN (i.e., ResNet18) and transformation functions (i.e., g, and h) for attention as in supervised learning. In each task, we sample the same number of classes for training and test, and follow the training procedure in [8]. For a fair comparison, all baselines and our model are trained on the same number of classes for all training tasks, since increasing the number of classes in training tasks improves the performance as indicated in [8]. We initialize the learning rate as and halve it after every 10k iterations. Our model is trained by ADAM [64] using a mini-batch size of 128 (only in the pre-training stage), a weight decay of 0.0001, and a momentum of 0.9. We train the model for 25k iterations in total. Given the class hierarchy, the training objective sums up the cross entropy losses computed over the coarse class and over the fine classes, respectively. All hyper-parameters are tuned based on the validation set introduced in Table 2. Every baseline and our method use the same training set and test test, and the test set is inaccessible during training so any data leakage is prohibited. In every experimental setting, we make the comparison fair by applying the same backbone, same training and test data, the same task setting (we follow the most popular N way K shot problem setting) and the same training strategy (including how to sample tasks and the value of N and K for meta-learning, since higher N and K generally lead to better performance as indicated in [8]).

我们使用与监督学习中相同的主干CNN（即ResNet18）和转换函数（即g和h）进行注意力。在每项任务中，我们抽取相同数量的类别进行训练和测试，并遵循[8]中的培训程序。为了进行公平的比较，所有基线和我们的模型都在所有培训任务相同数量的类别上进行训练 ，因为增加训练任务中的类别数量可以提高效率，如[8]所示。我们将学习速率初始化为，并在每10k迭代后将其减半。ADAM[64]使用128的小批量（仅在预训练阶段）、0.0001的重量衰减和0.9的动量对我们的模型进行了训练。我们总共训练了25k次迭代的模型。给定类的层次结构，训练目标分别对粗类和细类计算的交叉熵损失进行汇总。所有超参数均根据表2中介绍的验证集进行调整。每个基线和我们的方法都使用相同的训练集和测试，并且在训练期间无法访问测试集，因此禁止任何数据泄漏。在每个实验环境中，我们通过应用相同的主干、相同的训练和测试数据、相同的任务设置（我们遵循最流行的N-way K shot问题设置）和相同的训练策略（包括如何对任务进行抽样以及元学习中的N和K值，因为N和K值越高，通常会产生更好的性能，如[8]所示）来进行公平比较。

5.3.2 Experiments on mcfsImageNet

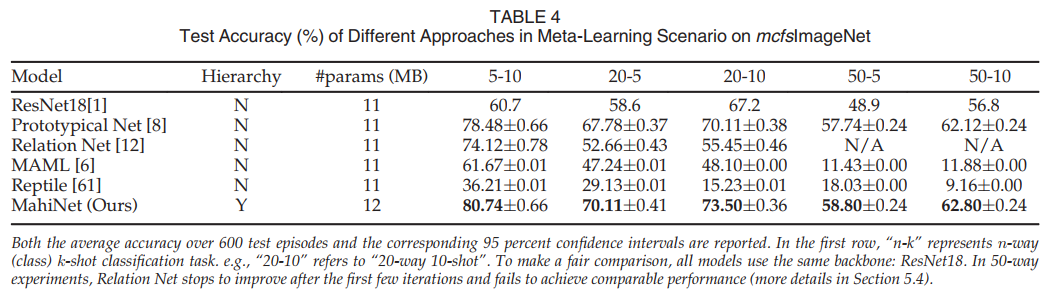
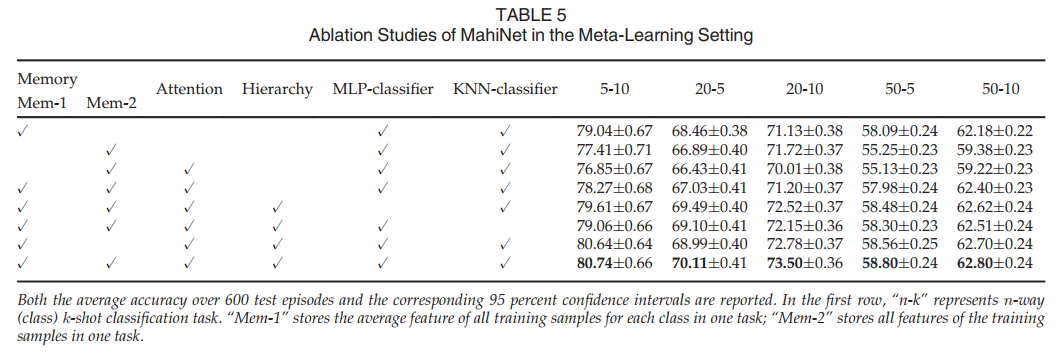
Table 4 shows that MahiNet outperforms the supervised learning baseline (ResNet18) and the meta-learning baseline (Prototypical Net). For ResNet18, we use the fine-tuning introduced in [6], in which the trained network is first fine-tuned on the training set (i.e., the support set) provided in the new task in the test stage and then tested on the associated query set. To evaluate the contributions of each component in MahiNet, we show results of several variants in Table 5. “Attention” refers to the parametric functions for g and h, otherwise we use identity mapping. “Hierarchy” refers to the assist of class hierarchy. For a specific task, “Mem-1” stores the average embedding over all training samples for each class in one task; “Mem-2” stores all the embeddings of the training samples in one task; “Mem-3” is the union of “Mem- 1” and “Mem-2”. Table 5 implies: (1) Class hierarchy information can incur steady performance across all tasks; (2) Combining “Mem-1” and “Mem-2” outperforms using either of them independently; (3) Attention brings significant improvement to MCFS problem only when being trained with class hierarchy. Because the data is usually insufficient to train a reliable similarity metric to distinguish all fine classes, but distinguishing a few fine classes in each coarse class is much easier. The attention module is merely parameterized by the two linear layers g and h, which are usually not expressive enough to learn the complex metric without the side information of class hierarchy. With the class hierarchy as a prior knowledge, the attention module only needs to distinguish much fewer fine classes within each coarse class, and the learned attention can faithfully reflect the local similarity within each coarse class. We also show the number of parameters for every method in the table. Our method only has 9 percent more parameters compared to baselines.

表4显示，MahiNet优于监督学习基线（ResNet18）和元学习基线（原型网络）。对于ResNet18，我们使用了[6]中介绍的微调，其中首先在测试阶段的新任务中提供的训练集（即支持集）上微调训练网络，然后在关联查询集上测试。为了评估MahiNet中每种成分的贡献，我们在表5中展示了几种变体的结果。“注意”指的是g和h的参数函数，否则我们使用恒等式映射。“层级”指的是阶级层级的辅助。对于特定任务，“Mem-1”存储了一个任务中每个类的所有训练样本的平均嵌入量；“Mem-2”将训练样本的所有嵌入存储在一个任务中；“Mem-3”是“Mem-1”和“Mem-2”的结合。表5表明：（1）类层次结构信息可以在所有任务中产生稳定的性能；（2） 结合使用“Mem-1”和“Mem-2”的效果优于单独使用其中任何一种；（3） 只有在进行类别等级培训时，注意力才能显著改善MCFS问题。因为数据通常不足以训练一个可靠的相似性度量来区分所有的细类，但是在每个粗类中区分几个细类要容易得多。注意模块仅由两个线性层g和h进行参数化，这两个层的表达能力通常不足以在没有类层次结构的辅助信息的情况下学习复杂的度量。将类层次结构作为先验知识，注意模块只需要在每个粗类中区分较少的细类，所学习的注意可以忠实地反映每个粗类中的局部相似性。我们还显示了表中每个方法的参数数量。与基线相比，我们的方法只多了9%的参数。

5.3.3 Experiments on mcfsOmniglot

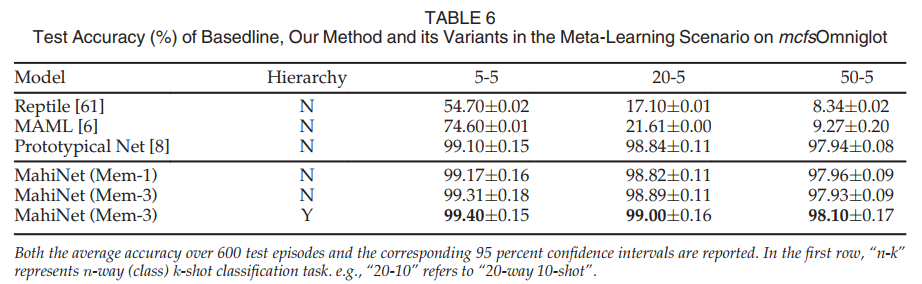
We conduct experiments on the secondary benchmark mcfsOmniglot. We use the same training setting as for mcfsImageNet. Following [65], mcfsOmniglot is augmented with rotations by multiples of 90 degrees. In order to make an apple-to-apple comparison to other baselines, we follow the same backbone used in their experiments. Therefore, we use four consecutive convolutional layers, each followed by a batch normalization layer, as the backbone CNN and compare MahiNet with prototypical networks as in Table 6. We do ablation study on MahiNet with/without hierarchy and MahiNet with different kinds of memory. “Mem-3”, i.e., the union of “Mem-1” and “Mem-2”, outperforms “Mem-1”, and “Attention” mechanism can improve the performance. Additionally, MahiNet outperforms other compared methods, which indicates the class hierarchy assists to make more accurate predictions. In summary, experiments on the small-scale and large-scale datasets show that class hierarchy brings a stable improvement.

我们在二级基准mcfsOmniglot上进行了实验。我们使用与mcfsImageNet相同的训练设置。在[65]之后，mcfsOmniglot增加了90度的旋转倍数。为了与其他基线进行apple-to-apple的比较，我们遵循了他们实验中使用的相同主干。因此，我们使用四个连续的卷积层，每个层后面都有一个批量标准化层，作为主干CNN，并将MahiNet与表6中的原型网络进行比较。我们对具有/不具有层次结构的MahiNet和具有不同类型记忆的MahiNet进行了研究。“Mem-3”即“Mem-1”和“Mem-2”的结合，其表现优于“Mem-1”，而“注意”机制可以提高表现。此外，MahiNet优于其他比较过的方法，这表明类层次结构有助于做出更准确的预测。总之，在小规模和大规模数据集上的实验表明，类层次结构带来了稳定的改进。

5.4 Comparison to Variants of Relation Net

5.4.1 Relation Network With Class Hierarchy

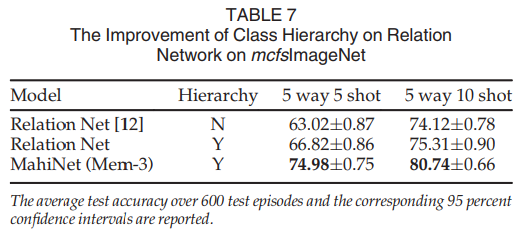
In order to demonstrate that the class hierarchy information and the multi-output model not only improves MahiNet but also other existing models, we train relation network with class hierarchy in the similar manner as we train MahiNet. The results are shown in Table 7. It indicates that the class hierarchy also improves the accuracy of relation network by more than 1 percent, which verifies the advantage and generality of using class hierarchy in other models. Although the relation net with class hierarchy achieves a better performance, MahiNet still outperforms this improved variant due to its advantage in its model architecture, which are specially designed for utilizing the class hierarchy in the many-class few-shot scenario.

为了证明类层次信息和多输出模型不仅改进了MahiNet，而且也改进了其他现有模型，我们以与训练MahiNet类似的方式训练具有类层次的关系网络。结果如表7所示。结果表明，类层次结构还使关系网络的准确度提高了1%以上，验证了在其他模型中使用类层次结构的优越性和通用性。尽管具有类层次结构的关系网实现了更好的性能，但MahiNet仍然优于这种改进的变体，因为它在模型体系结构方面具有优势，这种模型体系结构是专门为在多类少样本场景中利用类层次结构而设计的。

 5.4.2 Relation Network in Many-Class Setting

When relation network is trained in many-class settings using the same training strategy from [12], we found that the network usually stops to improve and stays near a sub-optimal solution. Specifically, after the first few iterations, the training loss still stays at a high level and the training accuracy still stays low. They do not change too much even after hundreds of iterations, and this problem cannot be solved after trying different initial learning rates. The training loss quickly converges to around 0.02 and the training accuracy stays at ~ 2% no matter what learning rate is applied to the training procedure. Relation net on other low way settings have a competitive performance as shown in Table 7, which is also the settings reported in their papers. We use the same hyperparameters as their paper for both few-class and many-class settings and the difference is only the parameter of the number of way. Even if relation network performs well in the fewclass settings, its performance dramatically degrade when given the challenging high-way settings. One potential reason for this is that relation net uses MSE loss to regress the relation score to the ground truth: matched pairs have similarity 1 and mismatched pair have similarity 0. When the number of ways increases, the imbalance between the number of matched pairs and unmatched pairs grows and training is mainly to optimize the loss generated by the mismatched pairs instead of the matched ones, so that the objective focuses more on how to avoid mismatching instead of matching, i.e., predicting correctly, and makes the accuracy more difficult to get improvement. This suggests that relation networks may need more tricky way to train it successfully in a many-class setting compared to the few-class settings and traditional few-class few-shot learning approaches may not be directly applied in many-class few-shot problems. This is also one of the drawbacks for relation net and how to make the model more robust to hyper-parameter tuning is beyond the scope of our paper.

当使用[12]中相同的训练策略在多个类别设置中训练关系网络时，我们发现该网络通常会停止改进，并保持在次优解附近。具体来说，在最初几次迭代之后，训练损失仍然保持在较高水平，训练精度仍然保持较低。即使经过数百次迭代，它们也不会有太大的变化，而且在尝试不同的初始学习速率后，这个问题无法解决。无论对训练过程应用何种学习率，训练损失迅速收敛到0.02左右，训练精度保持在2%左右。如表7所示，其他低端设置的关系网具有竞争性性能，这也是他们论文中报告的设置。对于少数类和多类设置，我们使用与论文相同的超参数，不同之处仅在于路径数的参数。即使关系网络在少数类设置中表现良好，但在具有挑战性的高速设置下，其性能也会显著降低。其中一个潜在原因是，关系网使用MSE损失将关系分数回归到基本事实：匹配对的相似度为1，不匹配对的相似度为0。当方法的数量增加时，匹配对和不匹配对之间的不平衡会增加，训练主要是优化不匹配对而不是匹配对产生的损失，因此目标更侧重于如何避免不匹配而不是匹配，即正确预测，并使准确性更难得到提高。这表明关系网络可能需要更复杂的方法来在多类环境中成功地训练，而传统的少类少样本学习方法可能无法直接应用于多类少镜头问题。这也是关系网的缺点之一，如何使模型对超参数调整更具鲁棒性超出了本文的范围。

5.5 Analysis of Hierarchy

The main reasons of the improvement in our paper are: (1) our model can utilize prior knowledge from the class hierarchy; (2) we use an effective memory update scheme to iteratively and adaptively refine the support set. We show how much improvement the class hierarchy can bring to our model in Table 5 and to other baselines in Table 7. The upper half of Table 5 are variants of our model without using hierarchy while the lower half are variants with hierarchy. It shows that the variants with hierarchy consistently outperform the ones without using hierarchy. To see whether hierarchy can help to improve other baselines, in Table 7, we add hierarchy information to relation net (while keeping the other components the same) and it achieves 1-4 percent improvement on accuracy.

本文改进的主要原因是：（1）我们的模型可以利用来自类层次结构的先验知识；（2） 我们使用一种有效的内存更新方案来迭代和自适应地优化支持集。我们展示了类层次结构可以给表5中的模型和表7中的其他基线带来多大的改进。表5的上半部分是我们模型的变体，不使用层次结构，而下半部分是带有层次结构的变体。结果表明，具有层次结构的变体始终优于不使用层次结构的变体。为了了解层次结构是否有助于改善其他基线，在表7中，我们将层次结构信息添加到关系网中（同时保持其他组件不变），从而使准确性提高1-4%。

5.6 Analysis of Augmented Memory

5.6.1 Visualization

In order to show how representative and diverse the feature vectors selected into the memory slots are, we visualize them together with the unselected images’ feature vectors using tSNE in Fig. 3 [66]. In particular, we randomly sample 50 fine classes marked by different colors. Within every class, we show both the feature vectors selected into the memory and the feature vectors of the original images from the same class. The features in the memory (crosses with a lower transparency) can cover most areas where the image features (dots of a higher transparency) are located. It implies that the highly selected feature vectors in memory are diverse and sufficiently representative of the whole class.

为了展示选择到存储槽中的特征向量的代表性和多样性，我们使用图3[66]中的tSNE将它们与未选择图像的特征向量一起可视化。特别是，我们随机抽取了50个用不同颜色标记的精细类。在每一类中，我们都会显示选择到内存中的特征向量和来自同一类的原始图像的特征向量。内存中的特征（透明度较低的十字）可以覆盖图像特征（透明度较高的点）所在的大部分区域。这意味着在内存中高度选择的特征向量是多样的，足以代表整个类。

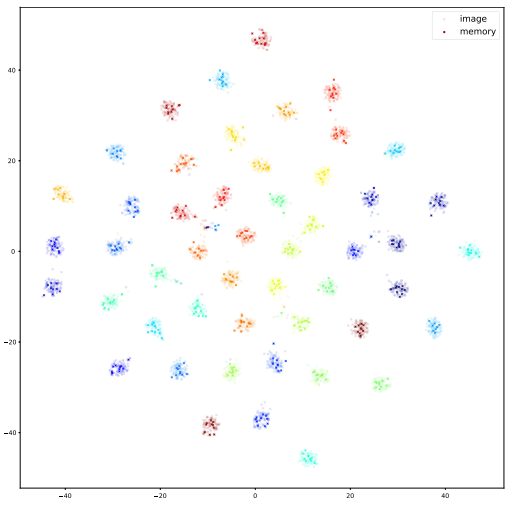
Fig. 3. The t-SNE visualization for memory maintained in the setting of supervised learning. We randomly sample 50 out of 754 fine classes shown as different colors. The sampled image feature of the training samples and the stored memory feature for one class share the same color while the image feature has higher transparency. For each class, the image features surround the memory feature and features from different classes are dispersed from each other for classification. =  t-SNE记忆可视化是在监督学习环境下进行的。我们随机抽取了754个不同颜色的精细类别中的50个。训练样本的采样图像特征与一个类别的存储记忆特征具有相同的颜色，而图像特征具有更高的透明度。对于每个类别，图像特征围绕着记忆特征，来自不同类别的特征相互分散以进行分类。

5.6.2 Memory Cost

In the supervised learning experiments, the memory load required by MahiNet is only 754 * 12=125; 321= 7.2% (12 samples per class for all the 754 fine classes, while the training set includes 125,321 images in total) of the space needed to store the whole training set. We tried to increase the memory size to about 10 percent of the training set, but the resultant improvement on performance is negligible compared to the extra computation costs, meaning that increasing the memory costs is unnecessary for MahiNet. In contrast, for meta-learning, in each task, every class only has few-shot samples, so the memory required to store all the samples is very small. For example, in the 20-way 1-shot setting, we only need to store 20 feature vectors in the memory. Therefore, our memory costs in both supervised learning and meta-learning scenarios can be kept small and the proposed method is memory-efficient.

在监督学习实验中，MahiNet所需的记忆负荷仅为754*12=125；321=存储整个训练集所需的空间的（所有754个精品班每类12个样本，而训练集总共包括125321个图像）。我们试图将内存大小增加到训练集的10%左右，但与额外的计算成本相比，由此产生的性能改善微不足道，这意味着MahiNet不需要增加内存成本。相比之下，对于元学习，在每个任务中，每个类只有少量样本，因此存储所有样本所需的内存非常小。例如，在20-shot设置中，我们只需要在内存中存储20个特征向量。因此，在监督学习和元学习场景中，我们的记忆成本都可以保持很小，并且所提出的方法是高效的。

6 总结

In this paper, we study a new problem “many-class few-shot” (MCFS), which is a more challenging problem commonly encountered in practice compared to the previously studied “many-class many-shot”, “few-class few-shot” and “few-class many-shot” problems. We address the MCFS problem by training a multi-output model producing coarse-to-fine predictions, which leverages the class hierarchy information and explore the relationship between fine and coarse classes. We propose “Memory-Augmented Hierarchical-Classification Network (MahiNet)”, which integrates both MLP and learnable KNN classifiers with attention modules to produce reliable prediction of both the coarse and fine classes. In addition, we propose two new benchmark datasets with a class hierarchy structure and multi-label annotations for the MCFS problem, and show that MahiNet outperforms existing methods in both supervised learning and meta-learning settings on the benchmark datasets without losing advantages in efficiency.

在本文中，我们研究了一个新的问题“多类少样本”（MCFS），这是一个在实践中经常遇到的比以前研究的“多类多样本”、“少类少样本”和“少类多样本”问题更具挑战性的问题。我们通过训练一个产生从粗到精预测的多输出模型来解决MCFS问题，该模型利用类层次结构信息，并探索精类和粗类之间的关系。我们提出了“记忆增强层次分类网络（MahiNet）”，它将MLP和可学习KNN分类器与注意模块相结合，以产生对粗类和细类的可靠预测。此外，我们还针对MCFS问题提出了两个新的具有类层次结构和多标签注释的基准数据集，并表明MahiNet在基准数据集的监督学习和元学习设置上都优于现有方法，同时又不会失去效率优势。