水体渲染小结_水体着色

最近接触了水体渲染，发现水体渲染这一块所涉及到的知识非常的多，所以这里就来总结一下大概有的知识点，并展示一下一些粗略的水体效果。

因为水体渲染实在是太多，因为考虑到开发环境是移动端，一切都以性能为主而去尽量还原水体，我通过XMIND编写了一个思维导图，下面先展现水体渲染的一个大致的思路。

简单概括水体渲染可以分为两大块，分别是水体着色和水体动画，因为本demo是使用一块面片来模拟水体，所以一些比较复杂的效果会比较难以实现，毕竟考虑到移动端的性能问题，而且在里面也有很多细分的技术，下面便一一介绍。

1.反射颜色

我们把水体着色分为两个模块，分别为反射颜色和折射颜色，在计算完对应的反射和折射效果后，我们通过菲涅耳方程得到反射和折射的比例，最后乘上相应的颜色，便是最终的水体颜色了，下面介绍反射颜色。

1.1反射

我们知道水体，在视角与水面夹角较小时，我们可以看到很多物体在水面的倒影，这是水体的反射，对于实现水体的反射，我们一般有四种做法。
第一种就是最常见的采样天空盒，它适用于静态的物体，但对于动态的物体有交互的话就非常容易穿帮。
第二种就是Unity内置的反射探针，通过把画面烘焙到反射探针上，水面实时读取探针里的内容进行反射。
前两种都是最为常见的反射方法，最后两种分别为平面反射(PlanerReflection)，屏幕空间反射SSR(Screen Space Reflection)。而平面反射就是该demo用到的方法，我们着重介绍一下。
平面反射的原理就是在原位置放置一台与主摄像机参数一致的摄像机，然后通过MV矩阵的变换，再乘以R的反射矩阵。它的意义是把相机的位置转换为相对于平面对称的相机空间，最后通过投影矩阵输出RT进行采样，而因为本demo使用的是一个面片，刚好对应着平面，且效果来说比上述都要好。
最后就是屏幕空间反射SSR了，这应该是以后主流的反射技术，一般在pc端使用的比较多，它的原理是从当前点，逆着光线的方向进行光线追踪，然后把光线碰到的物体的深度值和屏幕空间深度做比较，如果大于就写入。光线追踪技术是以后实时渲染的重要环节，现在完全模拟光追的话还较为困难，但是一些近似的方法，一些小trick还是非常的多的，等下一次有机会再深入了解一下。
下面上一些关键代码：

挂在水面上的脚本：
定义一个反射相机，并定义反射矩阵，与相机位置的MV矩阵相乘

var reflectM = CaculateReflectMatrix();
reflectionCamera.worldToCameraMatrix = Camera.current.worldToCameraMatrix * reflectM;
1
2

定义投影矩阵，把相机变换到反射相机空间，防止因物体在水面下方却依然反射的情况，把视锥体的近裁剪面给替换掉，并且使用了Unity内置的api CalculateObliqueMatrix函数进行计算。

var normal = transform.up;
var d = -Vector3.Dot(normal, transform.position);
var plane = new Vector4(normal.x, normal.y, normal.z, d);
//用逆转置矩阵将平面从世界空间变换到反射相机空间
var clipMatrix = reflectionCamera.CalculateObliqueMatrix(plane);
reflectionCamera.projectionMatrix = clipMatrix;
1
2
3
4
5
6

最后把相机渲染得到的RT赋值给shader，并进行采样，这里通过采样一张噪波图，对反射得到图像进行偏移，模拟水面的倒影的扰动。最后考虑到平面反射到的区域有限，我们同样计算了通过采样天空盒得到反射颜色，并对两者进行插值，系数可以根据自己想要的效果来定，最后得到最终的反射颜色

//计算环境光平面反射
float2 screenUV = scrpos.xy / scrpos.w;
float2 uvOffset = N.xz * pow(noise,3);
screenUV += uvOffset;
fixed4 reflcol = tex2D(_ReflectionTex,screenUV);

float3 reflectDir = normalize(reflect(-V,N));//计算反射向量 使用该方向对CubeMap进行取样
float3 iblSpecular = UNITY_SAMPLE_TEXCUBE(unity_SpecCube0,reflectDir);
/插值合并反射颜色
reflcol.rgb = lerp(reflcol.rgb,iblSpecular,0.4);
1
2
3
4
5
6
7
8
9
10

下面是反射的效果图

我们可以看到在边缘区域会稍微亮一点点，在最后调节效果时，我把天空盒的采样改为了pbr里的线性采样，最终的效果如下

加上法线贴图后的效果

2.折射颜色

计算完反射颜色后，我们可以开始计算折射颜色了，我把折射模块分成了5个小点，下面便来一一介绍。

2.1水体基本色(BaseCol)

对于水体的基本色，我们是基于水体的深度来讨论的。在日常生活中，一般浅水区的水颜色较为清澈，颜色也比较浅，而深水区一般颜色会较深，也不容易看清底部。基于这一点，我们可以得出两个结论。水的颜色和透明度会随着深度呈一个线性变化，那么水体基本色的渲染核心便定下了。
那我们如何获取水体的深度呢？在常规做法里，在Unity里，我们可以通过开启相机的深度模式，拿到相机渲染出的深度图。然后我们把水体的渲染队列改为Transparent，这样就可以优先得到所有水体下的物体的深度。最后通过拿到当前渲染物体的深度，两者相减在做出些许处理，就可以得到一个深度系数了。

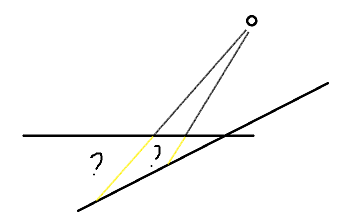
上图问号，便是我们求得的深度系数，对于水体的颜色，我们可以自己定义一个最浅和最深的颜色，然后根据深度进行插值。也可以通过一张渐变颜色图，根据深度系数进行采样，具体看效果来定，该demo是使用了最浅和最深的颜色进行水体颜色的渲染，因为采样会增加性能上的负担，下面上代码：

在相机上挂上该代码脚本，获取深度图

GetComponent<Camera>().depthTextureMode = DepthTextureMode.Depth;
1

Shader里定义深度图和水体颜色

_DeepWaterCol("DeepWaterCol",Color) = (0.353, 0.47, 0.561, 1)
_ShallowWaterCol("ShallowWaterCol",Color) = (0.275, 0.855, 1, 1)

sampler2D _CameraDepthTexture;
1
2
3
4

在顶点着色器上，我们通过 ComputeScreenPos() 函数把裁剪空间里的顶点转换成屏幕空间的坐标，并把顶点的z通过 COMPUTE_EYEDEPTH() 函数转成视角空间，因为在视角空间里，顶点的z坐标的负数为相机到该顶点的距离，即 -z。而该函数已经帮我们封装好了。

o.scrpos = ComputeScreenPos(o.pos);
COMPUTE_EYEDEPTH(o.scrpos.z);
1
2

然后我们就可以根据深度系数求得水体颜色，介绍一下里面几个内置的函数api，LinearEyeDepth是把采样得到的深度是视锥体的深度范围转成视角空间里的深度值，另外还有一个api是Linear01Depth，这个是把上述的深度值在进一步处理，映射到(0,1)的区间。深度图的采样坐标为屏幕坐标，在采样前，需要进行齐次除法进行处理，而SAMPLE_DEPTH_TEXTURE_PROJ帮我们处理好了，直接使用屏幕坐标即可。然后就是对系数做一个简单的处理，就可以得到我们的基础色了。

//根据高度插值颜色
float d = LinearEyeDepth(SAMPLE_DEPTH_TEXTURE_PROJ(_CameraDepthTexture, UNITY_PROJ_COORD(scrpos)));
depth = pow(saturate((d - scrpos.z)* 0.3),0.3);
float4 Albedo = lerp(_ShallowWaterCol,_DeepWaterCol,depth);
1
2
3
4

下面上效果图：

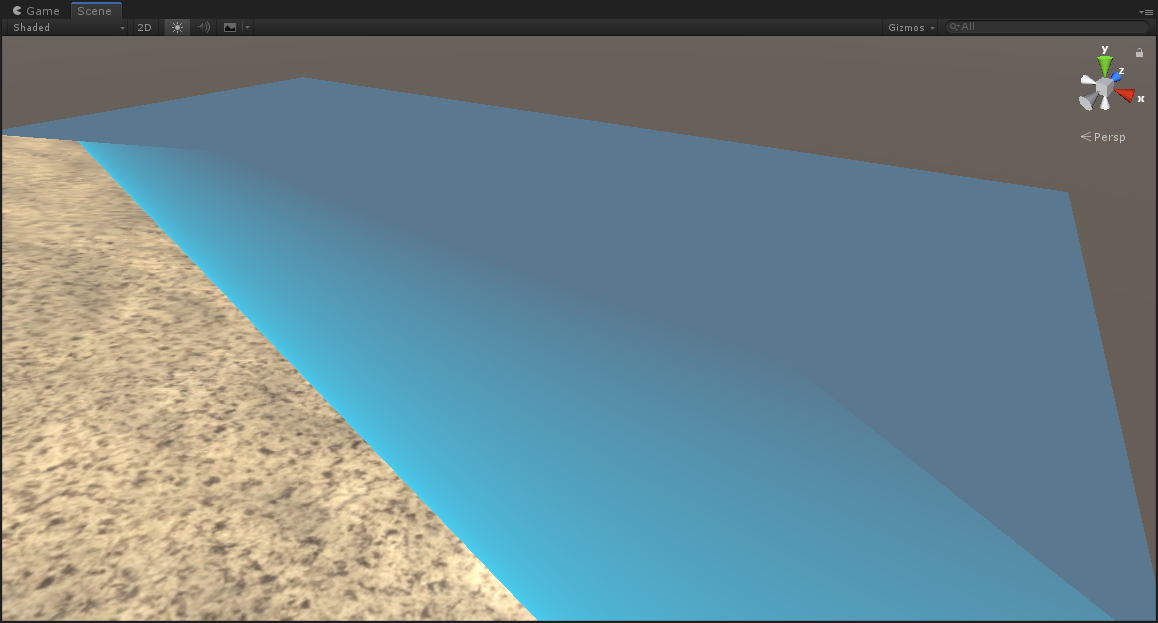
可以看出颜色有一个过渡，我们可以根据个人的感观来修改深浅颜色信息和对深度做一定的处理。最后，我们把计算得到的折射颜色和反射颜色通过菲涅耳系数进行混合。

菲涅耳方程

float3 fresnelSchlick(float cosTheta,float3 F0)
{
         return F0 + (1 - F0) * pow(1.0 - cosTheta,5.0);
}
1
2
3
4

计算得到反射和折射的比例，并通过插值得到最终结果。

float3 Ks = fresnelSchlick(max(dot(N,V),0.0),F0);
float4 finalcolor = lerp(refrcol,reflcol,Ks.r);
1
2

效果如下：

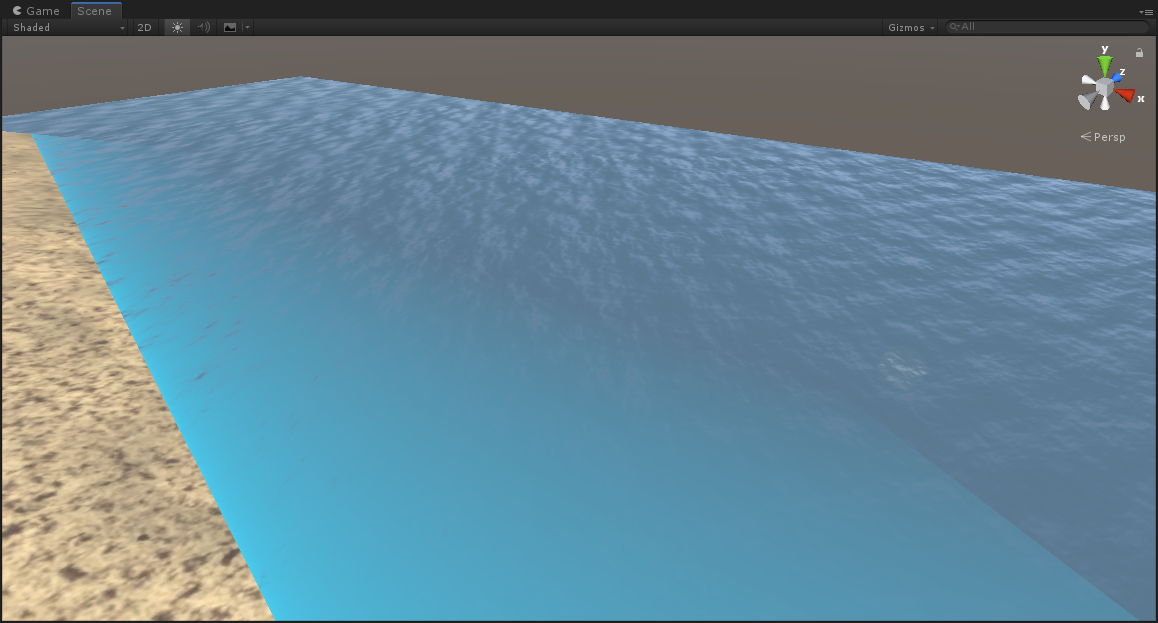
2.2折射(Refraction)

在一些浅水区，我们看水下的物体一般会发生折射效果，至于做法也是非常常规了，就是通过抓屏，然后扰动采样，最后混合原颜色就可以实现了，也没有什么技术难点，下面列出关键代码：
一般水越深，折射效果越强，所以在采样偏移上，我们可以乘上之前计算得到的深度系数，再乘以一个切线空间下的法线和噪波图得到扰动系数，最后得到结果。

//对水下进行折射采样偏移
float2 offset = tangentN.xy * noise * depth * 0.3;
scrpos.xy += offset;
float2 screenUV = scrpos.xy / scrpos.w;
float4 refrcol = tex2D(_RefractionTex,screenUV);
1
2
3
4
5

效果如下：

我们把水体的基本色和折射得到的颜色做一个线性插值，它的参数为水体的深度，因为水越深，水底的东西越难看清，代码如下：

//计算水深衰减最终颜色;
refrcol = lerp(refrcol,Albedo,saturate(depth * _AlphaScale));
1
2

最终效果如下：

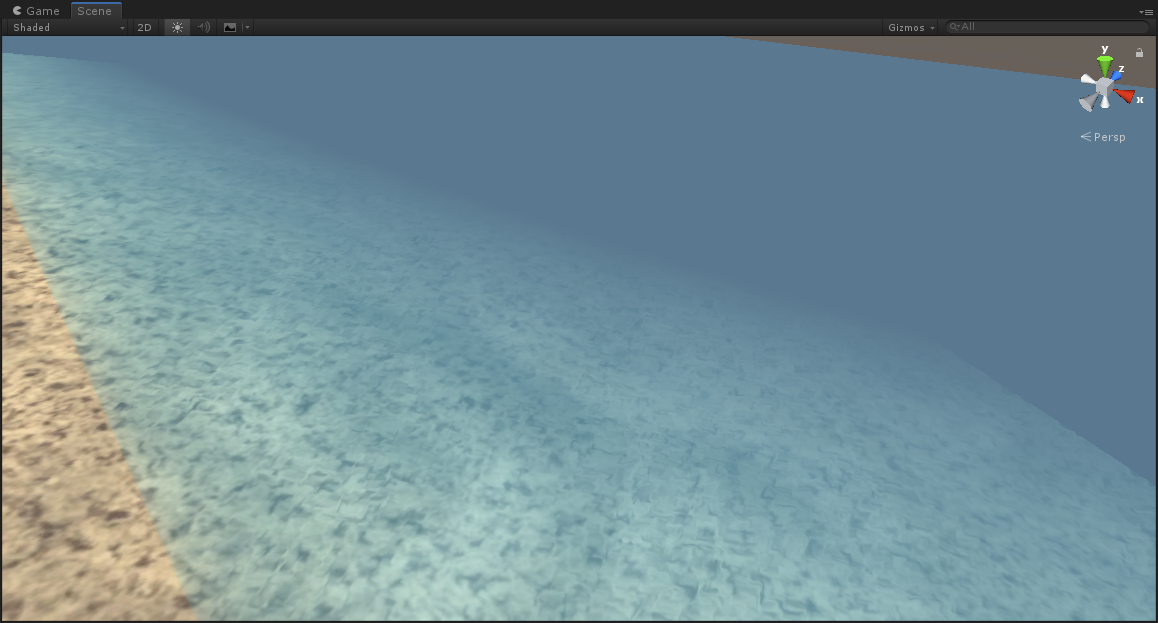
最后在和反射颜色混合

2.3通透感-次表面散射(SSS)

我们知道水体在不断运动时会产生波浪，这个时候光照在穿过水体时不止会发生折射，还会产生次表面散射，即光线在内部经过多次反射后又折射了出来，具体的表现便是，入射光一侧没有想象中的亮，而其他没被光线照射到的地方没有想象中的暗，整体呈一种比较温润的效果。而在实时渲染里，计算每一条光路的去向显然不太实际，所以这里用到了一种近似的快速次表面散射算法进行计算，它是在GDC2011上，Frostbite寒霜引擎提出的模拟，代码如下：

其中 _SSSDistortion是对法线的偏移，值越大，散射的越厉害。_SSSPower和 _SSSScale也是控制效果的参数，具体效果可以根据个人来调节，最后我们把计算得到的结果和折射颜色直接相加即可，因为本demo并没有涉及涉及到波浪，所以具体效果因具体项目而议。

float3 CalculateSSSColor(float3 L,float3 V,float3 N)
            {
                float3 H = normalize(L + N * _SSSDistortion);
                float I = pow(saturate(dot(V,-H)),_SSSPower) * _SSSScale;
                return _SSSColor * I;
            }
1
2
3
4
5
6

比较效果图，分别为无SSS和有SSS

2.4焦散(Causitcs)

一些基本的水体的物理效果已经实现了，接下来我们就要实现水体的一些特殊物理现象，比如焦散。首先，对于焦散的定义来说，它是指当光线穿过一个透明物体时，由于对象表面的不平整，使得光线折射并没有平行发生，出现漫折射，投影表面出现光子分散。而在浅水区，水体的焦散效果是非常明显的，这里通过一种生成焦散的算法FBM，得到焦散的颜色，并把它与折射颜色相加。代码如下：

下面这三个函数就是生成了焦散的颜色，实则它是噪声算法的一种，通过voronoi算法进行位置固定，再通过FBM生成噪波，最后得到结果。

float2 hash22(float2 p)
            {
                float3 p3 = frac(float3(p.xyx) * HASHSCALE3);
                p3 += dot(p3, p3.yzx+19.19);
                return frac((p3.xx+p3.yz)*p3.zy);
            }
            //voronoi 算法
            float wnoise(float2 p,float time)
            {
                float2 n = floor(p);
                float2 f = frac(p);
                float md = 5.0;
                float2 m = float2(0.,0.);
                for (int i = -1;i<=1;i++) 
                {
                for (int j = -1;j<=1;j++) 
                {
                float2 g = float2(i, j);
                float2 o = hash22(n+g);
                o = 0.5+0.5*sin(time+6.28*o);
                float2 r = g + o - f;
                float d = dot(r, r);
                if (d<md) 
                {
                  md = d;
                  m = n+g+o;
                } 
                }
                }
                return md;
            }
            //FBM 集合操作sum
            float3 CausticColor(float2 p,float time) 
            {
                float v = 0.0;
                float a = 0.4;
                for (int i = 0;i<3;i++)
                {
                  v+= wnoise(p,time)*a;
                  p*=2.0;
                  a*=0.5;
                }
                v = pow(v,2.)*5.;
                return float3(v,v,v);
            }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

这里传入的参数为屏幕的UV和一个速度参数，因为该水体是一个面片，所以是在水面表现出来的。但是在日常生活中，焦散应该在水底的位置，所以这里的屏幕UV其实可以通过之前计算到的深度信息进行还原，但是我没研究出来。其次，对颜色乘上了一个以深度为基地的焦散系数，最后得到焦散颜色。

//水下焦散计算
float2 CausticUV = UV * _CausticTilling;
float Causticspeed = _Time.y * _CausticSpeed;
float3 Causticcolor = CausticColor(CausticUV,Causticspeed) * _CausticPower;
float CausticK = saturate((1 - depth) * 5);
1
2
3
4
5

效果图如下：

2.5浪花白沫(Foam)

在生活中，我们可以看到运动的水体会因为碰撞而产生浪花和白沫，而我们可以把这些浪花白沫分成三种，浪尖白沫、岸边白沫、交互白沫，本demo涉及到的只有岸边白沫，所以接下来便着重说一下岸边白沫。
对于岸边白沫的渲染，我使用了刺客信条3基于Multi Ramp Map的方法。简单来说就是在一张贴图的RGB通道里，分别放置稠密、中等、稀疏的三张灰度图，同时定义一张ramp图，定义三者之间的混合比例。更通俗的讲就是采样一张灰度图和ramp图，并把它们的通道两两相乘，最后三个通道加在一起就为白沫的颜色了。这里考虑到采样涉及的性能问题，我把ramp定义的比例改为了自己设置的数值，代码如下：

这里因为考虑到海滩和普通的湖泊的区别，所以使用了一个变体和Toggle进行区分两种不同的水体。最后再把得到的白沫颜色和折射颜色相加即可。

                //边缘浪花
                float2 foamoffset;
                float foamK;
                float3 foamCK;
                #if _MOVE_ON
                foamoffset = 1 - depth + sin(_Time.y);
                foamK = _FoamPower * pow((1 - depth),1.5) * saturate(sin(-_Time.y));
                foamCK = float3(1,1,1.5);
                #else
                foamoffset = 0;
                //对深度做平方 使边缘更聚集
                foamK = _FoamPower * pow((1 - depth),3);
                foamCK = float3(1,2,5);
                #endif
                float3 foam = tex2D(_FoamMap,UV + foamoffset);
                float3 foamc = tex2D(_FoamRamp,UV);
                float3 foamcolor = (foam.r * foamCK.r + foam.g * foamCK.g + foam.b * foamCK.b) * foamK;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

效果图如下：

海滩上的海浪白沫：

湖泊水流引起的白沫：

我们可以看到在水体和陆地的切边会非常的硬，那是因为透明度的问题，我们同样根据透明度进行插值，越浅的地方水体越透明，让水和陆地完美融合。

refrcol.a = lerp(0,1,depth);
1

效果如下：

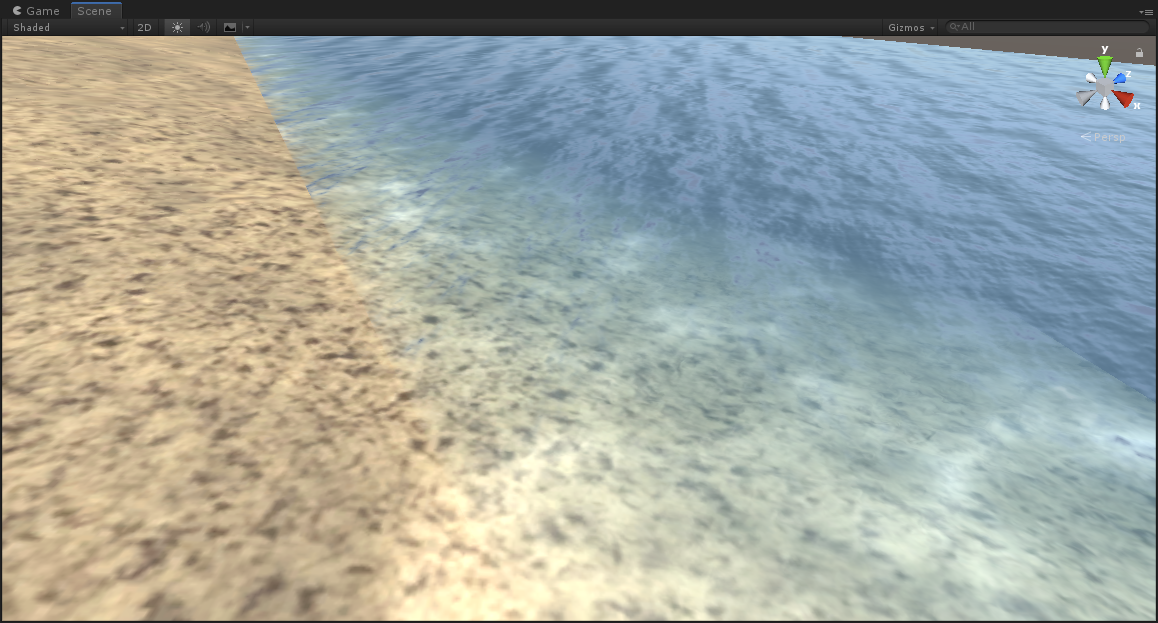
最后我们在最终颜色上，加上高光，即可得到最后的效果，高光用的模型就是普通的Blinn-Phong模型。效果图如下：

3.水体流动(Flow)

水体流动一直是水体渲染的一大难点，对于不同的水体，它流动的表现形式也有所不同。对于溪流河流来说，它的流动是有方向的，速度可以湍急也可以缓慢。对于湖泊来说，一般流动的效果不会太明显，所以涉及到的波形也较为平缓。对于大海来说，它的流动更为的无序且粗犷，波峰也相应的更大。
而对于如何实现水体流动，我们一般分为两种实现，一种是通过改变水体的顶点，实现顶点运动表现出流动感。第二种即为只改变法线，因为光照受到法线的影响，所以水体看起来是”运动”的。本demo使用的是第二种，因为顶点动画的在性能上会有一定的影响，所以并没有采用。下面就详细介绍一下两种方法。

3.1顶点波形动画(Vertex Animation)

因为顶点动画在该demo里并没有使用到，所以会大概讲一下实现的思路和理解。

3.1.1正弦波(Sin)

水体常见的波形正弦波sin函数，它的函数非常适合模拟水的顶点流动，非常平滑和圆润，但是唯一缺点就是太过于规律化，一般比较适合池塘、湖泊这种水体。而根据函数图，我们可以根据对应的变量更改它的波峰或是频率。

3.1.2Gerstner波

Gerstner波是正弦波的进化版，它对比于正弦波来说，它的波峰更加尖锐，波谷宽阔，一般比较适合海洋等比较粗犷的水体。下图便清晰的看到Gerstner波的每个顶点都在做圆周运动，目前使用该波形在水体渲染的领域的应用非常广泛，许多大型3A都采用该波形进行渲染。不过一般情况下，无论是正弦波还是Gerstner波，我们都会使用叠加的方式使用，让水体表面更加复杂无序。

3.1.3快速傅里叶变换(FFT)

傅里叶变换是一种线性的积分变换，它一般用于信号在时域和频域之间的变换。而快速傅里叶变换(FFT)就是在nlogn时间内完成高效的计算的统称。而在水体渲染领域里，我们一般通过理论或者统计数据获得海浪的频谱(一般使用Phillips频谱)，结合正弦波在频谱中生成波形的分布，最后用逆FFT得到高度图，在经过一定的处理，我们可以得到置换贴图(Displacement map)。有了置换贴图，我们也可以通过数据导出表面的法线贴图或者白沫贴图等等。

3.1.4波动粒子(Wave Particles)

还有一种模拟波形的方法，就是波动粒子(Wave Particles)。它首次在2007年由Yuksel提出，该方法的核心是用粒子代表每一个水波，并且可以与动态对象的互动，水波的复杂度降低为平面上的粒子移动，是模拟实时水体交互非常不错的方案。
波动粒子实际就是通过波动方程模拟每一个粒子对表面的影响，它们相互并不会影响，只会衰减和分散。

在神秘海域3里，该游戏使用了在环形区域中放置随机分布的粒子，从而近似的模拟水体的上下波动，最终把该区域制作成一个向量位移场并让水体进行采样位移。而神秘海域4更是采用了多分辨率Wave Particles的方法，具体可以参阅更多的资料去了解。

3.1.5曲面细分(Tessellation)

这里引入了一个新的知识点叫曲面细分，我们都知道顶点动画是对顶点进行操作，如果一个平面只有两个顶点时，它能做的只有折叠，并不能做到像波浪一样起伏，而Unity自带的plane面片里的顶点显然不是特别的多。如果我们去修改模型，去添加顶点的话，又会对性能上有损耗。这里引入一个新的技术，就是曲面细分，它主要的功能是通过添加多边形，实现对模型精度上的影响，从而提高模型的表现能力。
在曲面细分里，该技术引入了Hull shader和Domain shader两个关键的单元，而Hull shader主要负责了LOD细分的等级，Domain主要通过贴图控制模型的形变，而这些都是曲面细分的一些原理。而在Unity里，这些已经帮我们封装好了，用表面着色器(surface shader)时非常容易实现的，但我们写的是顶点片元着色器，所以我们需要定义自己的曲面细分着色器，具体代码如下：

我们需要定义使用的shader

#pragma vertex tessvert_surf
#pragma fragment frag
#pragma hull hs_surf
#pragma domain ds_surf
1
2
3
4

实际上我们先自己定义一个tessvert_surf作为曲面细分着色器的一个输入，然后通过自己定义的hs_surf为拿到数据，hsconst_surf则定义了我们该如何进行细分，比如根据距离细分等，而ds_surf则是重新对细分后的顶点进行法线、切线等数据的计算，最后再把顶点传给我们原来自己定义的顶点着色器，最后完成曲面细分。

//曲面细分
// tessellation vertex shader
            struct InternalTessInterp_appdata_base 
            {
                float4 vertex : INTERNALTESSPOS;
                float4 tangent : TANGENT;
                float3 normal : NORMAL;
                float4 texcoord : TEXCOORD0;
            };
            InternalTessInterp_appdata_base tessvert_surf (appdata_tan v) 
            {
                InternalTessInterp_appdata_base o;
                o.vertex = v.vertex;
                o.tangent = v.tangent;
                o.normal = v.normal;
                o.texcoord = v.texcoord;
                return o;
            }

            // tessellation hull constant shader
            UnityTessellationFactors hsconst_surf (InputPatch<InternalTessInterp_appdata_base,3> v) 
            {
                UnityTessellationFactors o;
                float4 tf;
                tf = _TessellateAmount;
                o.edge[0] = tf.x; o.edge[1] = tf.y; o.edge[2] = tf.z; o.inside = tf.w;
                return o;
            }

            // tessellation hull shader
            [UNITY_domain("tri")]
            [UNITY_partitioning("fractional_odd")]
            [UNITY_outputtopology("triangle_cw")]
            [UNITY_patchconstantfunc("hsconst_surf")]
            [UNITY_outputcontrolpoints(3)]
            InternalTessInterp_appdata_base hs_surf (InputPatch<InternalTessInterp_appdata_base,3> v, uint id : SV_OutputControlPointID) {
                return v[id];
            }

            // tessellation domain shader
            [UNITY_domain("tri")]
            v2f ds_surf (UnityTessellationFactors tessFactors, const OutputPatch<InternalTessInterp_appdata_base,3> vi, float3 bary : SV_DomainLocation) {
                appdata_tan v;UNITY_INITIALIZE_OUTPUT(appdata_tan,v);
                v.vertex = vi[0].vertex*bary.x + vi[1].vertex*bary.y + vi[2].vertex*bary.z;
                v.normal = vi[0].normal*bary.x + vi[1].normal*bary.y + vi[2].normal*bary.z;
                v.tangent = vi[0].tangent*bary.x + vi[1].tangent*bary.y + vi[2].tangent*bary.z;
                v.texcoord = vi[0].texcoord*bary.x + vi[1].texcoord*bary.y + vi[2].texcoord*bary.z;
                v2f o = vert (v);
                return o;
            }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50

效果图如下：

3.2预渲染(Pre-Render)

在上述讲到的顶点动画中，大部分都是通过实时计算顶点需要偏移的位置，尤其是FFT的方法，庞大的计算量对于移动端来说要难以支持。所以，这里引入了预渲染的方法，即提前把需要的数据准备好，使用时直接读取数据即可。下面便一一介绍预渲染表现水体流动的几种方法。

3.2.1法线偏移(Normal Map)

法线偏移是最常见的一种实现物体表面移动的方法了，对于水体流动来说，它的效果虽然没有顶点那么真实，但是对于一些湖泊等流动上下波动不是那么明显的水体来说也是够用了。
具体的方法就是对采样的法线进行一个时间的偏移，代码如下：

float3 N1 = UnpackNormal(tex2D(_NormalMap,float2(i.uv.x + frac(_WaveSpeedX * _Time.y),i.uv.y - frac(_WaveSpeedY * _Time.y))));
float3 N2 = UnpackNormal(tex2D(_NormalMap,float2(i.uv.x - frac(_WaveSpeedX * _Time.y),i.uv.y + frac(_WaveSpeedY * _Time.y))));
float3 N = normalize(N1 + N2);
1
2
3

可能唯一的问题是，水体流动过于单一，且可能眼睛会稍微有些许眼花，这在后续会继续想办法完善。

3.2.2流型图(Flow Map)

对于一些比较复杂的流向时，法线偏移显然无法满足我们的要求，这里引入一个 流型图(Flow Map) 的概念，它是一张存储了一个二维的方向向量的贴图，通常存储在R、G通道。我们通过采样得到方向，并进行偏移，它更适合溪流又或是难以进行实时计算的非线性运动。这里有一款非常方便的软件进行流型图的制作，具体在以前的文档有提到过，网上也可以查阅到。

3.2.3离线FFT贴图烘焙(Offline FFT Texture)

在预渲染里，刚刚提到的FFT也可以进行离线烘焙。该方法首次由刺客信条3的团队提出，它们通过预计算提前烘焙出一系列的高度图，再把高度图转变为置换贴图(displacement map)、法线贴图(normal map)、 白沫图(Foam map) 等等，最后通过序列帧的方法将贴图进行采样，最后就可以得到FFT的水体了。

4.水体交互(Interaction)

在水体交互上，主要有几个点需要了解到。首先就是刚刚提到过的波动方程，在物体接触水面后，产生的水波，我们就需要波动方程去计算，模拟水波的扩散。其次就是当物体与水面移动过快时，会产生白浪，即上面说过的交互白沫。
对于波动方程来说，实现并不难，简单来说就是拿到当前触发点的坐标，代入到水波纹扩散公式中，即波动方程，然后用两张RT进行循环计算，而水体shader只需读取其中一张RT，并计算更改后的顶点信息和法线信息和切线信息就可以实现实时的交互。
对于交互白沫，在本demo里并没有实现，可以在后续完善补充。
代码如下：

通过采样RT，进行顶点的偏移，该步骤可省略，避免对顶点的操作产生性能影响。

o.uv.zw = v.texcoord;
float4 waveTransmit = tex2Dlod(_CurrentRT,float4(o.uv.zw,0,0));
float waveHeight = DecodeFloatRGBA(waveTransmit) * _VertexMoveAmount;
v.vertex.y += waveHeight;
1
2
3
4

该步骤为采样得到的灰度图，通过差分法求得法线，即通过求某个点的两个切向量，然后通过叉积得到交互后的法线。

float2 delu = float2(_CurrentRT_TexelSize.x * _RebulidNormalScale,0);
float h1_u = tex2D(_CurrentRT,i.uv.zw - delu).r;
float h2_u = tex2D(_CurrentRT,i.uv.zw + delu).r;
float3 tangent_u = float3(delu.x,0,h2_u - h1_u);

float2 delv = float2(0,_CurrentRT_TexelSize.y * _RebulidNormalScale);
float h1_v = tex2D(_CurrentRT,i.uv.zw - delv).r;
float h2_v = tex2D(_CurrentRT,i.uv.zw + delv).r;
float3 tangent_v = float3(0,delv.y,h2_v - h1_v);
float3 N3 = normalize(cross(tangent_v,tangent_u));
1
2
3
4
5
6
7
8
9
10

最后效果如下：

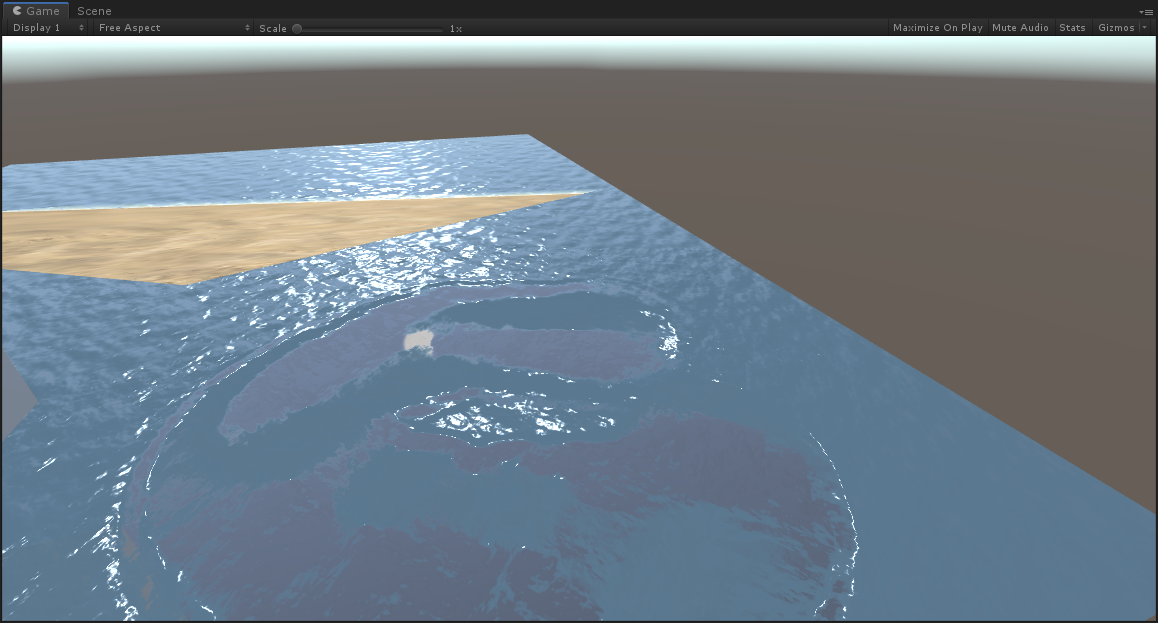
水体渲染大致的流程就总结到这里，其实还有很多细节没有讲清楚，也还有许多不同的做法没有介绍到，以后有时间会继续完善这一模块的知识体系，进行总结。

参考:

1.真实感水体渲染技术总结
2.一波江水动京城：游戏水面渲染与互动
3.水体渲染小结
4.从零开始的水渲之形状Shape[二]
5.游戏中的实时水体模拟技术
6.Fast Subsurface Scattering in Unity (Part 1)
7.Unity曲面细分的原理与应用2
8.中级Shader教程23 voronoi算法
9.Unity Shader-反射效果（CubeMap，Reflection Probe，Planar Reflection，Screen Space Reflection）
10.Unity只在一个面片上实现真实水体渲染
11.【Unity教程】可实时交互的涟漪效果
12.如何在Unity实现从纹理中生成法线贴图？
13.FlowMap的使用
14.Texture Distortion