菜单导航
1、常用数学公式： 等差/等比数列通项和求和、指数、对数、排列组合等
一、常用数学公式
1.0 实数：有理数和无理数的总称，常用字母R表示实数集；
有理数是整数和分数的集合，有理数的小数部分是有限或者无限循环的数；小数部分为无限不循环的数为无理数；
自然数：全体非负整数组成的集合，常用字母N来表示
质数：又称素数，大于1的自然数中，除了1和它本身以外不再有其他因数；因数：又叫约数，整数a除以整数b(b≠0)的商正好是整数而没有余数，则b是a的因数；
幂：乘方的结果。a = n^m, 指m个n相乘，把n^m乘方的结果a叫做幂，也叫n的m次幂；
1.1 等差数列
定义：一个数列从第二项起，每一项与它的前一项的差等于同一个常数。这个数列就叫做等差数列，这个常数也叫等差数列的公差，公差常用字母d表示。
通项公式： , a1为等差数列首项，公差为d,
为 第n项
求和公式： ， Sn为数列前n项之和
-
等差中项：等差数列中，若有n+m=2*r, 则任意两项
的关系为：
其他：跟等差数列知识相关的一个有趣故事是：“高斯求和”
1.2 等比数列
定义：一个数列从第二项起，每一项与它的前一项的比等于同一个常数。这个数列就叫做等比数列，这个常数也叫等比数列的公比，公比通常用字母q表示。
通项公式：
（n∈N*）,当q>0时，可把
看做是自变量n的函数，点(n, 
)是曲线 
上的一群孤立的点。
求和公式：
或 
（q≠1）。
等比中项：
； 即等比数列中，若q+p = 2r, 则有
， 
为
等比中项。
其他：跟等比数列知识相关的一个有趣故事是：“棋盘上的麦粒”
1.3 指数函数
定义：一般地，函数
(a为常数且以a>0，a≠1)叫做指数函数, 函数的定义域是R，自变量x就叫做指数，常数a叫底数。
对于一切指数函数来讲，值域为(0， +∞)；指数函数的前系数为1；
指数型函数：y = 
(k≠1), 格式像指数函数，但不是指数函数；
幂函数：一般地，y=xα（α为有理数）的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数。
例如函数y=x0 、y=x2、y=x-1（注：y=x-1=1/x、y=x0时x≠0）等都是幂函数。
指数函数常用公式：
1.3.1： 
； 
； （同底相乘，指数相加；同底相除，指数相减）
1.3.2： 
（指数的指数，指数相乘）
1.3.3：
1.4 对数函数
定义：一般地，对数函数以幂（真数）为自变量，指数为因变量，底数为常量的函数。
比如ax = n（a>0，且a≠1），那么数x叫做以a为底n的对数，记作x=logan，读作以a为底n的对数，其中a叫做对数的底数，n叫做真数。
一般地，函数y=logax（a>0，且a≠1）叫做对数函数，也就是说以幂（真数）为自变量，指数为因变量，底数为常量的函数，叫对数函数。
常用公式：
1.4.1 ：
； 
； 负数和零无对数；
1.4.2 ： 
* 
= 1 ；
1.4.3 ： 
；
1.4.4：
1.4.5：
1.4.6：
1.4.7：
几张图表如下：
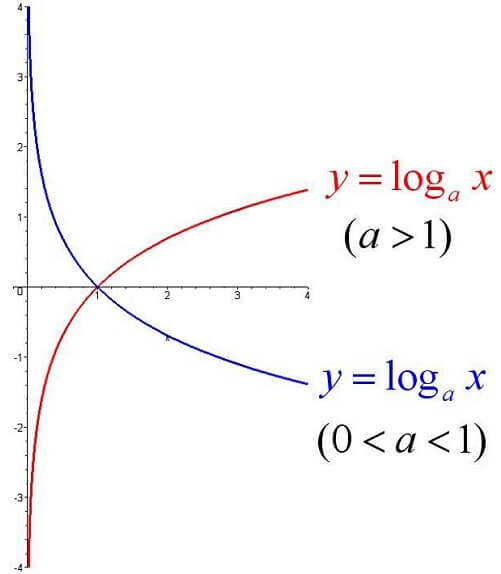
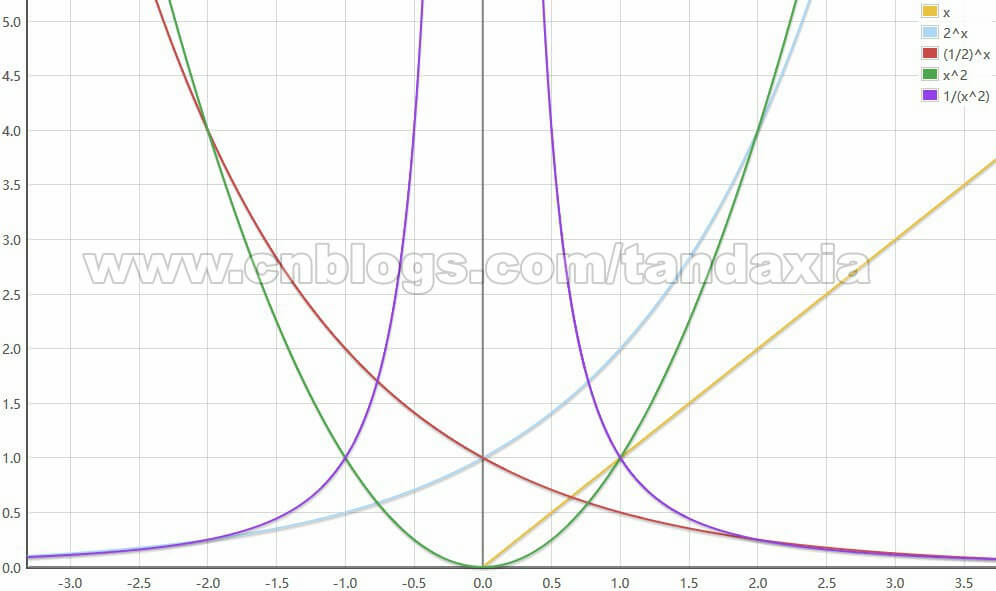
1.5 排列组合
1.5.1 阶乘：阶乘是指一个运算符号，一个正整数的阶乘（factorial）是所有小于及等于该数的正整数的积，并且0的阶乘为1。
自然数n的阶乘写作n!，亦即n!=1×2×3×...×n。阶乘亦可以递归方式定义：0!=1，n!=(n-1)!×n。
1.5.2 排列定义：从n个不同元素中，任取m(m≤n,m与n均为自然数,下同）个元素按照一定的顺序排成一列，叫做从n个不同元素中取出m个元素的一个排列；
从n个不同元素中取出m(m≤n）个元素的所有排列的个数，叫做从n个不同元素中取出m个元素的排列数，用符号 A(n,m）表示。
1.5.3 排列计算公式：
1.5.4 组合定义：从n个不同元素中，任取m(m≤n）个元素并成一组，叫做从n个不同元素中取出m个元素的一个组合；
从n个不同元素中取出m(m≤n）个元素的所有组合的个数，叫做从n个不同元素中取出m个元素的组合数。用符号 C(n,m) 表示。
1.5.5 组合计算公式：
1.5.6 排列和组合区别：排列是讲究排序的，而组合不考虑元素排序，一般来说，从n中不同元素取出m个元素的排列，要比组合数量多。
对于组合公式的理解，相对排列而言会绕一点，这里试图解释一下组合公式：
从n个不同元素中取出m个元素的所有组合个数，可以理解成先从n个不同的元素中取出m个元素的所有排列个数为Anm （即A(n, m) ），
然后因为m个元素的排序方式共有m!（即m*(m-1)*(m-2)*...*1, m的阶乘）种，而组合不考虑元素排序，相当于数量A(n, m)中重复了m!次，
所以排序数量A(n, m) 除以 排序方式数量m! , 则是我们需要的没有重复的组合数量了，即C(n, m) = A(n, m) / m!
二、逻辑且/或/非/异或，和余数
2.1 计算机为什么采用二进制计数法
2.1.1 在10进制计数法中，位数少，但是数字的种类多。（对于人类来说，比较易用）
2.1.2 在二进制计数法中，数字的种类少哦，但是位数多。（对于计算机来说，这种比较易用）
2.2 指数的法则：对于指数 a^n, n每减1，新的值就变成原来的1/a，即a^(n-1) 为 a^n的1/a
2.3 零的作用：用来表示占位；也用来统一标准，简化规则；
2.4 逻辑
命题：能够判断对错的陈述句叫做命题。命题正确时，则该命题为“真”（true）；反之，命题不正确时，称该命题为“假”（false）。
在建立规则时，需要确认规则有没有“遗漏”和“重复”；
没有“遗漏”，即完整性，明确此规则在什么情况下都能适用；没有“重复”，即具备排他性，明确此规则不存在矛盾之处。
逻辑从根本上说是对完整性和排他性的组合表达。
逻辑非：非真为假，非假为真；
逻辑且：A和B都为真时，才是真；A和B只要有一个为假，则为假；
逻辑或：A和B只要有一个为真，则结果为真；A和B都为假，则为假；
逻辑异或：A和B一真一假，则结果为真；A和B都为真，或者都为假，则结果为假；
德·摩根定律：“非A”或者“非B”, 和非“A与B”是等价的； “非A”并且“非B”，和非“A或B”是等价的；
2.5 卡诺图：简化复杂逻辑表达式的有效工具
2.5.1 二灯游戏（绿灯、黄灯）：
规则：1）绿灯灭，黄灯亮；
2）绿灯、黄灯灭；
3）绿灯、黄灯都亮
命题A : 绿灯亮
命题B : 黄灯亮
逻辑表达式为：(非A 并且 B) 或者 (非A 并且 非B) 或者 (A 并且 B)
卡诺图表示法（打上钩）：
2.5.3 三灯游戏 （绿灯、黄灯、红灯）
规则：1）绿灯、黄灯、红灯都灭
2）黄灯灭、红灯亮
3）绿灯灭、黄灯亮
4）绿灯、黄灯、红灯都亮
命题A : 绿灯亮
命题B : 黄灯亮
命题C : 红灯亮
逻辑表达式：(非A 且 非B 且 非C) 或 (非B 且 C) 或 (非A且 B) 或 (A且B且C)
卡诺图表示法（打钩）：
2.6 余数的作用：分组，将较大的数字除一次就能分组
2.6.1 思考题：今天是周三，那么100天后是周几？ 一亿天以后呢？（运用余数思考）
2.6.2 思考题：今天是周三，10^100天后是周几？（当计算有难度的时候，可以试图通过找规律来简化问题）
2.6.3 思考题：1234567^987654321的个位数是什么？（找规律：找出规律，再结合余数，把大数字简化成小数字）
2.6.4 思考题（黑白棋读心术）：
1）魔术师和他的徒弟在台上表演，台下有观众，魔术师蒙着眼睛，徒弟不允许说话，若干黑白棋(每个黑白棋像硬币样，只是一面黑色，一面白色)；
2）让观众在桌子上随机放7枚黑白棋的棋子排成一列。魔术师蒙着眼睛，看不到棋子；
3）让魔术师的徒弟在看完这7枚棋子后，在后面添加了一枚棋子，与其他棋子并排。这时有8枚棋子，魔术师依然蒙着眼睛；
4）这时让观众可以将其中1枚棋子翻转，或者不翻转任何棋子。此间，徒弟和观众不发一言，魔术师依然蒙着眼睛，不知道观众有没有翻转棋子；
5）魔术师摘下眼罩，观察8枚棋子，然后马上就能判断：“观众翻转了棋子” 或 “没有翻转棋子”，识破观众的行为。
问：魔术师是如何识破观众的行为的？
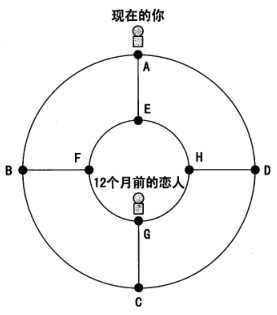
2.6.5 思考题（寻找恋人）：
在一个小王国中，有8个村子（A~H）。如下图所示，各个村之间道路相连（黑点表示村子，线表示道路）。而你要寻找流浪在这个王国的你唯一的恋人。
你的恋人住在这8个村子中的某一个里，她每过1个月便顺着道路去另一个村子，每个月都一定会换村子，然后选择哪个村子是随机的，预测不了。
例如：如果恋人这个月住在G村，那么下一个月可能会住在“F、C、H中的某一个村子“。
目前你手上掌握的确凿信息只是：1年前（12个月前），恋人住在G村。
现在问：这个月恋人住在A村的概率？（奇数、偶数）
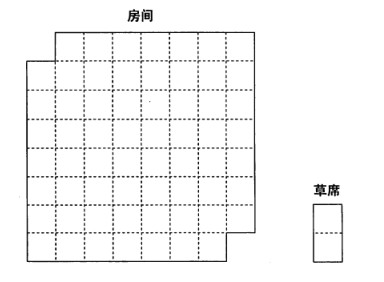
2.6.6 思考题（铺设草席）：
如下图所示，有这样一个房间，使用图中右下角所示的草席能够正好铺满房间吗？（前提是不能使用半张草席）
如果不能铺满的话，请说明理由？
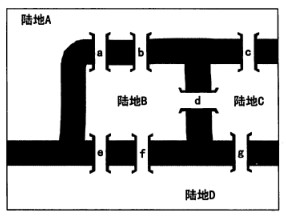
2.6.7 思考题（哥尼斯堡七桥问题）：
如下图所示，在很久以前，有一个叫哥尼斯堡的小城。小城被河流分割成了4块陆地。人们为了连接这些陆地，建设了7座桥。
现在要你找出走遍7座桥（a、b、c、d、e、f、g）的方法，但是，必须遵守以下条件：
1）走过的桥不能再走
2）可以多次经过同一块陆地
3）可以从任一陆地为起点
4）不需要再回到起点
最后，如果能够走遍7座桥的话，请说明一下方法。如果不能，也请证明一下。
三、数学归纳法
3.1 断言：断定一个特定前提为真的陈述
3.2 数学归纳法：数学归纳法是证明有关整数的断言对于0以上的所有整数（0、1、2、3...）是否成立时所用的方法。
3.3 数学归纳法的证明方法步骤：
1）步骤1：证明“P(0)成立”。步骤1也叫基底（base）
2）步骤2：证明不论k为0以上的哪个整数，“若P(k)成立，则P(k+1)也成立”。步骤2也叫归纳（induction）
若步骤1和步骤2都能得到证明，就证明了“断言P(n)对于0以上的所有整数n都成立”。
3.4 数学归纳法实例(求奇数的和)：
3.4.1 断言Q(n) : 1 + 3 + 5 + 7 + ... + (2*n-1) = n^2
3.4.2 用数学归纳法来证明“断言Q(n)对于1以上的所有整数n都成立”
3.4.3 步骤1：基底的证明
证明Q(1)成立。因为Q(1) = 1^2, 所以确实成立。步骤1证明完毕。
3.4.4 步骤2：归纳的证明
证明k为1以上的任意整数时，“若Q(k)成立，则Q(k+1)也成立”。
假设Q(k) = 1 + 3 + 5 + 7 + ... + (2*k-1) = k^2 成立
则来证明等式Q(k+1)成立
Q(k+1)的左边和右边计算结果相同。
由此，从Q(k)到Q(k+1)推导成功，步骤2得到了证明。
至此，通过数学归纳法的步骤1和步骤2都证明了断言Q(n)。也就是说，通过数学归纳法，证明了断言Q(n)对于1以上的任意整数n都成立。
四、递归
4.1 思考题（汉诺塔）：
有三根细柱（A、B、C）。A柱上套着6个圆盘。这些圆盘大小各异，按从大到小的顺序自下而上摆放。
现在要把A柱上的6个圆盘全部移到B柱上。并且在移动圆盘时须遵守以下规则：
1）一次只能移动柱子最上端的一个圆盘
2）小圆盘上不能放大圆盘。
将1一个圆盘从一根柱子移到另一根柱子，算移动“1次”。那么，将6个圆盘全部从A移到B最少需要移动几次呢？
（可以先通过3个圆盘、5个圆盘找出递归规律）
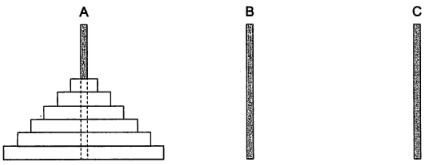
先来看看3层汉诺塔的解法（移动7次）：
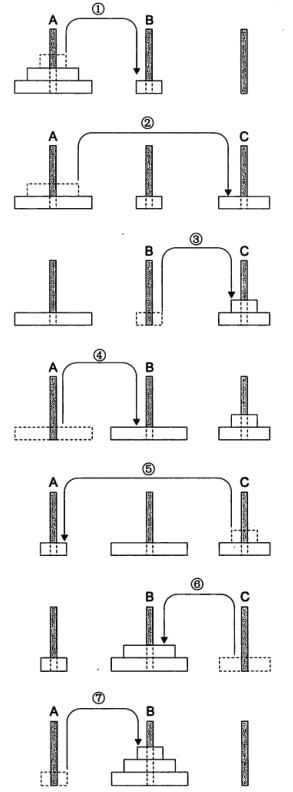
发现移动2个圆盘的规律：
4.2 递归的思维方式：将复杂问题转换成较为简单的同类问题。在问题中找出递归结构，根据递归结构建立递归公式。
4.3 思考题（不断繁殖的动物）：
有一种动物，它出生2天后就开始以每天1只的速度繁殖后代。假设第一天，有一只这样的动物（该动物刚出生，从第三天起繁殖后代）。
问到第11天，共有多少只？
五、指数爆炸
5.1 思考题（折纸问题）：
假设现在有一张厚度为1mm的纸，纸质非常柔软，可以对折无数次。每对折一次，厚度便翻一番。
已知地球距月球约39万公里，请问对折多少次后厚度能够超过月地距离呢？
5.2 指数爆炸：数字每次翻倍，然后我们会发现这种数字会急速增长。这种情况我们叫它“指数爆炸”，也可以称为“指数式增长”
5.3 思考题（寻找犯人，二分法查找）
有15个犯罪嫌疑人排成一排，其中只有一个是真正的“罪犯”。
你要通过问他们“罪犯在哪里？”来找出 真正的罪犯。
假设选择其中1人问：“罪犯在哪里？”会得到以下3钟答案，其中有一个是正确的。
1）“我是罪犯”（询问对象是罪犯时）
2）“罪犯在我左边”
3）“罪犯在我右边”
这时，仅通过3次问话就能从15人中找到真正的罪犯。那么，应该怎么问话呢？（找出地推结构以及递推公式）
六、反证法
6.1 反证法
1）首先，假设“命题的否定形式”成立
2）根据假设进行论证，推导出矛盾的结果
一言以蔽之，反证法就是“先假设命题的否定形式成立，然后再进行推理，引出矛盾”
6.2 反证法实例：为什么不存在“最大的整数”？
假设存在“最大的整数”，并将它设为M。
那么M+1就比M大，这与M是最大的整数的假设相矛盾。
因此不存在“最大的整数”。
6.3 反证法实例2：请证明质数是无穷的
假设“质数不是无穷的”，即“质数的个数是有限的”成立。
假设质数的个数是有限的，所以所有质数的集合就可以写为：
2,3,5,7，..., P
现在，将所有的质数（2,3,5,7，..., P）相乘，并设相乘的结果+1为Q。
即Q = 2*3*5*7*...*P + 1
因为假设质数是有限个的，所以这个Q的大小也是有限的。
而Q比所有的质数相乘的结果大1，因此Q比任何质数（2,3,5,7，...,P）都大。
“Q比任何质数都大”也就意味着“Q不是质数”。
另一方面，这个Q除以2,3,5,7，...，P中的任一一个数，余数都是1（不能整除）。
这就表明，Q只能被1和Q本身整除，所以根据质数的定义可得“Q是质数”。
因此“Q不是质数”和“Q是质数”都成立，这是矛盾的。
因此，通过反证法证明了“质数是无穷的”。
6.4 反证法的主意事项
反证法从“要证明的命题的否定形式”出发，即必须先假设错误的假设成立。
但到引出矛盾结论为止的论证过程本身必须正确，之所以这么说因为如果中途的论证出现错误，就不能得出“因为最初的假设错误，所以产生矛盾”的结论。
参考资料：百度百科，和《程序员的数学.（日）结城浩》
