obsidian技巧_obsidian 代码块

1、引用

Human beings face ever more complex and urgent problems, and their effectiveness in dealing with these problems is a matter that is critical to the stability and continued progress of society.

---

2、代码块

如果使用Tab键对段落进行缩进，这段文本在预览模式下也会被识别为代码块。
1

如果使用Tab键对段落进行缩进，这段文本在预览模式下也会被识别为代码块。	
1

3、行内代码

一行中被 反引号 括起来的文字会以代码格式显示。

---

4、数学公式

行内公式用单$

• 简单语法：$E=mc^2$$E=m{c}^2$
• LaTex语法：$$\begin{bmatrix}x\\y\end{bmatrix}$$
  $$\left[\begin{array}{c}x\\ y\end{array}\right]$$
  可使用公式编辑器：在线LaTeX公式编辑器

公式换行

在以

\begin{aligned}
……
\end{aligned}
1
2
3

\begin{split}
……
\end{split}
1
2
3

为首尾的公式内，以\\表换行，以&表对齐，如：

$$\begin{aligned}
KPI&=(N+S)W \\
PI&=N+S \\
I&=W
\end{aligned}$$
1
2
3
4
5

K P I = ( N + S ) W P I = N + S I = W

$$\begin{aligned} KPI&=(N+S)W \\ PI&=N+S \\ I&=W \end{aligned}$$ KPIPII​=(N+S)W=N+S=W​

$$\begin{split} 
loss&=(y_i-Q(s,a;\theta))^2 \\
&=(r+\gamma \max Q(s^{'},a^{'};\theta^{-})-Q(s,a;\theta)) ^2\\
\end{split}$$
1
2
3
4

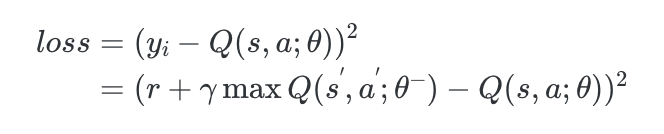
$$\begin{aligned} 
抽样定理:&一个频带限制在(0，f_{H})内的连续时间信号m(t)，\\
&如果以Ts≤1/(2f_{H})的间隔对其进行等间隔抽样，\\
&则m(t)将被这些抽样值完全确定。也就是说，\\
&如果以fs≥2f_{H}的抽样频率进行均匀抽样，\\
&m(t)可以被得到的抽样值完全确定。\\
&最小抽样频率fs=2f_{H}称为奈奎斯特频率，\\
&最大抽样间隔Ts=1/(2f_{H})称为奈奎斯特间隔。
\end{aligned}$$
1
2
3
4
5
6
7
8
9

抽 样 定 理 : 一 个 频 带 限 制 在 ( 0 ， f H ) 内 的 连 续 时 间 信 号 m ( t ) ， 如 果 以 T s ≤ 1 / ( 2 f H ) 的 间 隔 对 其 进 行 等 间 隔 抽 样 ， 则 m ( t ) 将 被 这 些 抽 样 值 完 全 确 定 。 也 就 是 说 ， 如 果 以 f s ≥ 2 f H 的 抽 样 频 率 进 行 均 匀 抽 样 ， m ( t ) 可 以 被 得 到 的 抽 样 值 完 全 确 定 。 最 小 抽 样 频 率 f s = 2 f H 称 为 奈 奎 斯 特 频 率 ， 最 大 抽 样 间 隔 T s = 1 / ( 2 f H ) 称 为 奈 奎 斯 特 间 隔 。

$$\begin{aligned} 抽样定理:&一个频带限制在(0，f_{H})内的连续时间信号m(t)，\\ &如果以Ts≤1/(2f_{H})的间隔对其进行等间隔抽样，\\ &则m(t)将被这些抽样值完全确定。也就是说，\\ &如果以fs≥2f_{H}的抽样频率进行均匀抽样，\\ &m(t)可以被得到的抽样值完全确定。\\ &最小抽样频率fs=2f_{H}称为奈奎斯特频率，\\ &最大抽样间隔Ts=1/(2f_{H})称为奈奎斯特间隔。 \end{aligned}$$ 抽样定理:​一个频带限制在(0，fH​)内的连续时间信号m(t)，如果以Ts≤1/(2fH​)的间隔对其进行等间隔抽样，则m(t)将被这些抽样值完全确定。也就是说，如果以fs≥2fH​的抽样频率进行均匀抽样，m(t)可以被得到的抽样值完全确定。最小抽样频率fs=2fH​称为奈奎斯特频率，最大抽样间隔Ts=1/(2fH​)称为奈奎斯特间隔。​

---

5、外部链接

外部链接:[百度](https://www.baidu.com)
百度

6、内部链接

1. 普通内部链接:[[线性代数]]
   [[线性代数]]
2. |更改显示的文本:[[线性代数|线代]]
   [[线性代数|线代]]
3. /路径索引，防重名:[[自然科学/数学/线性代数]]
   [[自然科学/数学/线性代数]]
4. #链接到标题:[[线性代数#矩阵（Matrix）]]
   [[线性代数#矩阵（Matrix）]]
5. ^链接到文本块，并更改显示的文本:[[线性代数#^8b822a|线性代数定义]]
   [[线性代数#^8b822a|线性代数定义]]
6. 链接并预览:![[线性代数]]
   ![[线性代数]]