【机器学习应用】【Python】决策树 Decision Tree_python 决策树

【机器学习应用】【Python】决策树 Decision Tree

决策树本质上是if/else语句的集合，通过回答一级一级的if/else问题，最终做出决策。比如，我们利用决策树来判断一个人是e人还是i人，可以形成以下决策树:

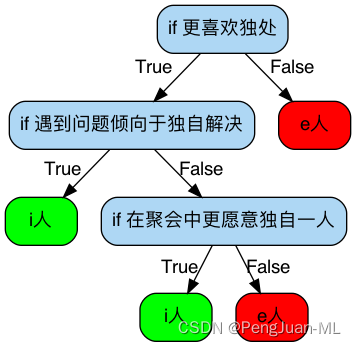
第一个问题被称为根节点(root)，之后的每一个分支节点被称为叶子(leaf)，这是一个深度为4，叶子为6的简单决策树。

决策树的形成

构建一棵决策树，不同的问题顺序，可能会得出不一样的结果。回到实际问题中，一组数据有多个特征，我们应该选择哪些特征构建决策树，如何决定顺序才能够达到更高的效率(更快、更准)呢？

抛开数学公式来理解，其实就是看哪一个特征能更有效地分类数据集。什么是更有效地分类？结合开头的例子，如果仅*“是否更喜欢独处“*这一个问题，回答“是”的人全都是i人，回答“不是”的全都是e人，一个问题就可以将e人/i人区分开，那么我们就认为，这是个有效问题。

但如果这个问题回答“是”的人中，i人和e人各占一半，那和掷骰子没什么区别，也就是一个没无效问题。

回到决策树算法中，衡量问题（也就是特征）是否有用/有效的指标，叫做基尼系数（也是经济学中用来衡量贫富差距的指标）。基尼系数根据数据集中各类别所占比例计算得出，根据一个特征分类后的数据集基尼系数越小，说明这个数据集的「贫富差距」越大

在社会生活中，我们不希望贫富差距越来越大，可在决策树中，分类后数据集的贫富差距越大越好，因其代表着这个分类特征更有效，更能把各类别区分开。

但在判断是否选取一个特征做节点时，考虑的是分类前数据集的基尼系数$gin{i}_{after}$是否小于未分类前的数据集的基尼系数$gin{i}_{before}$，如果$gin{i}_{before}\le gin{i}_{after}$，尽管$gin{i}_{after}$再小，也不算有效特征。$gin{i}_{before}$和$gin{i}_{after}$之间的差异称为信息增益，当一个特征带来的信息增益为正且在所有特征中最大时，决策树就选取这个特征做节点。

除此之外，我们也可以用信息熵来衡量一个特征是否有效。

信息熵用于衡量数据集中信息混乱程度，也就是一组数据里如果什么类别都有，信息熵就高，反之如果只有一种类别，信息熵为0.

根据基尼系数或信息增益，配合更详细的算法设计，我们可以将决策树算法分为三类：

• ID3决策树 - 信息熵
• C4.5决策树 - 信息增益率
• CART决策树 - 基尼系数+最多两个分支（也是sklearn中采用的算法）

再次回到决策树的形成，每次构建一个决策树，我们选取一个特征，然后计算这个特征的基尼系数或信息增益，选取基尼系数最小或信息增益最大的特征，作为第一个节点。对于分类出来的数据集，我们再测试并计算每一个特征的基尼系数或信息增益。

以此类推，直到最后我们将所有数据都分得清清楚楚，每一个最终节点上的数据，都是百分百纯正（同一类），我们就完成了一个决策树