花生_TL007

这个屌丝很懒，什么也没留下！

热门标签

神经网络背后的数学原理

作者：花生_TL007 | 2024-04-21 23:27:13

踩

神经网络背后的数学原理

原文地址：The Math Behind Neural Networks

2024 年 3 月 29 日

深入研究现代人工智能的支柱——神经网络，了解其数学原理，从头开始实现它，并探索其应用。

神经网络是人工智能（AI）的核心，为从发现照片中的物体到翻译语言的各种应用提供动力。在本文中，我们将深入探讨神经网络是什么，它们是如何工作的，以及为什么它们在当今技术驱动的世界中很重要。

1：基础知识

1.1：什么是神经网络？

神经网络是生物学和计算机科学的酷炫融合，灵感来自我们大脑处理复杂计算任务的设置。从本质上讲，它们是旨在发现模式和理解感官数据的算法，这使它们可以做很多事情，例如识别人脸、理解口语、做出预测和理解自然语言。

生物启示

我们的大脑有大约860亿个神经元，它们都连接在一个复杂的网络中。这些神经元通过称为突触的连接聊天，其中信号可以变强或变弱，从而影响传递的信息。这是我们学习和记忆事物的基础。

人工神经网络借鉴了本书的一页，使用分层连接的数字神经元或节点。您有接收数据的输入层、咀嚼这些数据的隐藏层以及吐出结果的输出层。当网络获得更多数据时，它会调整连接强度（或“权重”）来学习，有点像我们大脑的突触如何增强或减弱。

从感知器到深度学习

神经网络始于1958年一种叫做感知器的东西，这要归功于弗兰克·罗森布拉特（Frank Rosenblatt）。这是一个基本的神经网络，用于简单的“是”或“否”类型的任务。从那里，我们构建了更复杂的网络，如多层感知器（MLP），由于具有一个或多个隐藏层，它可以理解更复杂的数据关系。

然后是深度学习，它是关于具有许多层的神经网络。这些深度神经网络能够从大量数据中学习，它们是我们听到的许多人工智能突破的幕后推手，从击败人类围棋选手到为自动驾驶汽车提供动力。

通过模式理解

神经网络的最大优势之一是它们能够学习数据中的模式，而无需直接针对特定任务进行编程。这个过程被称为“训练”，让神经网络能够掌握总体趋势，并根据他们所学到的知识做出预测或决策。

由于这种能力，神经网络具有超强的通用性，可用于广泛的应用，从图像识别到语言翻译，再到预测股票市场趋势。他们正在证明，曾经被认为需要人类智能的任务现在可以通过人工智能来解决。

1.2：神经网络的类型

在深入研究它们的结构和数学之前，让我们先来看看我们今天可能发现的最流行的神经网络类型。这将使我们更好地了解他们的潜力和能力。我将在以后的文章中尝试涵盖所有这些内容，因此请务必订阅！

前馈神经网络（FNN）

从基础开始，前馈神经网络是最简单的类型。这就像数据的单行道——信息直接从输入端传输，穿过任何隐藏层，然后从另一端传到输出端。这些网络是简单预测和将事物分类的首选。

卷积神经网络（CNN）

CNN是计算机视觉领域的大佬。由于它们的特殊图层，它们具有捕捉图像中空间模式的诀窍。这种能力使他们在识别图像、发现其中的物体以及对他们所看到的事物进行分类方面成为明星。这就是您的手机可以在照片中区分狗和猫的原因。

递归神经网络（RNN）

RNN 具有各种记忆力，非常适合任何涉及数据序列的事情，例如句子、DNA 序列、笔迹或股票市场趋势。它们将信息循环回，使它们能够记住序列中以前的输入。这使他们在预测句子中的下一个单词或理解口语等任务中表现出色。

长短期记忆网络（LSTM）

LSTM 是一种特殊品种的 RNN，旨在长时间记住事物。它们旨在解决 RNN 在长序列中忘记内容的问题。如果您正在处理需要长时间保留信息的复杂任务，例如翻译段落或预测电视剧中接下来会发生什么，LSTM 是您的首选。

生成对抗网络（GAN）

想象一下，在猫捉老鼠的游戏中有两个人工智能：一个生成虚假数据（如图像），另一个试图捕捉什么是假的，什么是真的。那是 GAN。这种设置允许 GAN 创建令人难以置信的逼真图像、音乐、文本等。他们是神经网络世界的艺术家，从头开始生成新的、逼真的数据。

2：神经网络的架构

At the core of neural networks are what we call neurons or nodes, inspired by the nerve cells in our brains. These artificial neurons are the workhorses that handle the heavy lifting of receiving, crunching, and passing along information. Let’s dive into how these neurons are built.
神经网络的核心是我们所说的神经元或节点，其灵感来自我们大脑中的神经细胞。这些人工神经元是处理接收、处理和传递信息的繁重工作的主要力量。让我们深入了解这些神经元是如何构建的。

2.1：神经元的结构

神经元直接从我们感兴趣的数据或其他神经元的输出中获取输入。这些输入就像一个列表，列表中的每个项目都代表数据的不同特征。

对于每个输入，神经元都会做一些数学运算：它将输入乘以“权重”，然后添加“偏差”。将权重视为神经元决定输入重要性的方式，将偏差视为一种调整，以确保神经元的输出恰到好处。在网络训练期间，它会调整这些权重和偏差，以更好地完成工作。

接下来，神经元将所有这些加权输入和偏差相加，并通过称为激活函数的特殊函数运行总数。这一步是神奇的地方，允许神经元通过以非线性方式弯曲和拉伸数据来处理复杂的模式。此函数的常用选择是 ReLU、Sigmoid 和 Tanh，每种方法都有其调整数据的方式。

2.2：图层

具有 3 层的 FNN 架构 — 图片由作者提供

神经网络是分层结构的，有点像分层蛋糕，每一层由多个神经元组成。这些层的堆叠方式形成了网络的架构：

输入层

这是数据进入网络的地方。这里的每个神经元对应于数据的一个特征。在上图中，输入层是左侧的第一层，其中包含两个节点。

隐藏图层

这些是夹在输入和输出之间的层，从上图中可以看出。你可能只有一个或一堆这样的隐藏层，做着繁重的计算和转换工作。您拥有的层（以及每层中的神经元）越多，网络可以学习的模式就越复杂。但是，这也意味着需要更多的计算能力，并且网络更有可能过于沉迷于训练数据，这个问题被称为过拟合。

输出层

这是网络的最后一站，它在那里吐出结果。根据任务的不同，例如对数据进行分类，该层可能为每个类别都有一个神经元，使用类似于 softmax 函数的东西来给出每个类别的概率。在上图中，最后一层仅包含一个节点，表明该节点用于回归任务。

2.3：层在学习中的作用

隐藏层是网络的特征检测器。当数据在这些层中移动时，网络可以更好地发现和组合输入特征，将它们分层到对数据的更复杂的理解中。

随着数据通过的每一层，网络都可以拾取更复杂的模式。早期的图层可能会学习形状或纹理等基本知识，而更深的图层则掌握了更复杂的想法，例如识别图片中的物体或人脸。

3：神经网络的数学

3.1：加权总和

神经计算过程的第一步是将输入聚合到神经元中，每个输入乘以各自的权重，然后添加一个偏差项。此操作称为加权和或线性组合。在数学上，它表示为：

NN 的加权和公式 — 图片由作者提供

解释：

z 是加权和，
wi 表示与第 i 个输入相关的权重，
xi 是神经元的第 i 个输入，
b 是偏置项，这是一个唯一的参数，允许调整输出和加权和。

加权和至关重要，因为它构成了任何非线性变换之前神经元的原始输入信号。它允许网络对输入进行线性转换，调整神经元输出中每个输入的重要性（权重）。

3.2：激活函数

正如我们之前所说，激活函数在决定神经网络的输出方面起着关键作用。它们是决定神经元是否应该被激活的数学方程式。激活函数为网络引入了非线性属性，使其能够学习复杂的数据模式并执行超越单纯线性分类的任务，这对于深度学习模型至关重要。在这里，我们深入探讨了激活函数的几种关键类型及其意义：

Sigmoid 激活函数

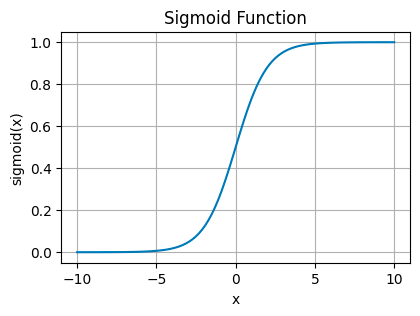
Sigmoid Plot — 图片由作者提供

此函数将其输入压缩到 0 到 1 之间的狭窄范围内。这就像取任何值，无论大小，并将其转换为概率。

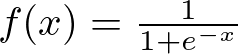
Sigmoid 函数 — 图片由作者提供

您将在二元分类网络的最后一层中看到 sigmoid 函数，您需要在两个选项之间做出决定——是或否、真或假、1 或 0。

双曲正切函数（tanh）

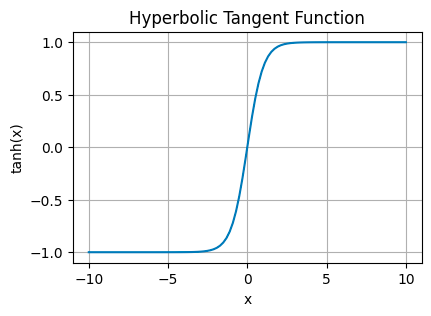
tanh Plot — 图片由作者提供

Tanh 将输出范围扩展到 -1 和 1 之间。这会使数据以 0 为中心，使下层更容易从中学习。

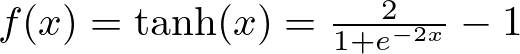
tanh formula — 图片由作者提供

它通常位于隐藏层中，通过平衡输入信号来帮助对更复杂的数据关系进行建模。

整流线性单元（ReLU）

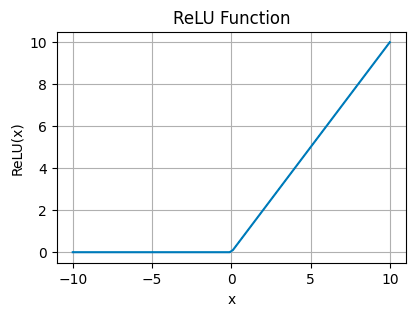
ReLU Plot — 图片由作者提供

ReLU 就像一个看门人，它传递正值不变，但阻止负值，将它们变为零。这种简单性使其非常高效，并有助于克服训练深度神经网络时的一些棘手问题。

ReLU 函数 — 图片由作者提供

它的简单性和效率使 ReLU 非常受欢迎，尤其是在卷积神经网络（CNN）和深度学习模型中。

泄漏整流线性单元（Leaky ReLU）

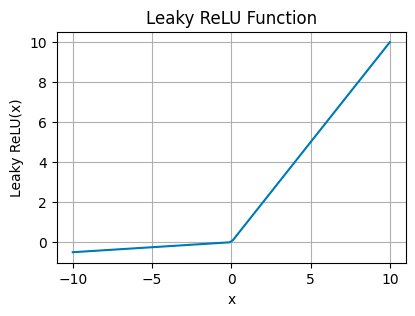
Leaky ReLU Plot — 图片由作者提供

当输入小于零时，Leaky ReLU 允许微小的非零梯度，即使神经元没有主动放电，它们也能保持活力和踢动。

Leaky ReLU — 图片由作者提供

这是对 ReLU 的调整，用于网络可能遭受“死亡神经元”的影响，确保网络的所有部分随着时间的推移保持活跃。

指数线性单位（ELU）

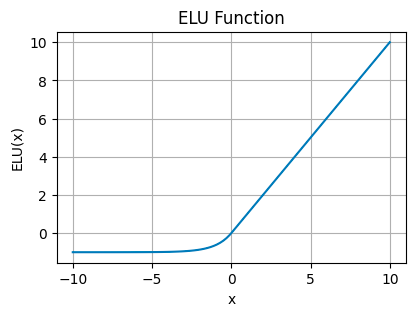
ELU Plot — 图片由作者提供

ELU 平滑负输入的函数（使用参数α进行缩放），允许负输出，但曲线平缓。这可以帮助网络保持接近于零的平均激活，从而改善学习动态。

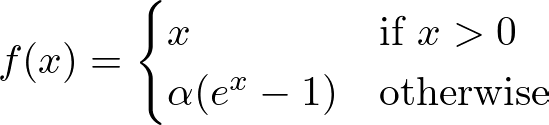
ELU 函数 — 图片由作者提供

在更深层次的网络中很有用，因为 ReLU 的尖锐阈值可能会减慢学习速度。

Softmax 函数

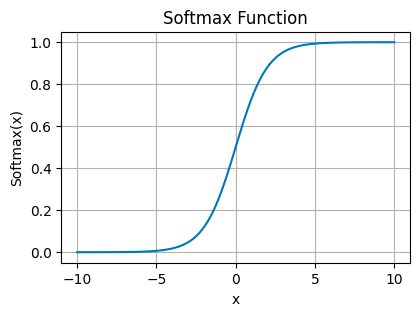
Softmax 函数 — 图片由作者提供

softmax 函数通过对 logit（神经元的原始输出分数）进行幂化和归一化，将其转换为概率。它确保输出值的总和为 1，使它们可直接解释为概率。

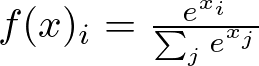
Softmax 函数 — 图片由作者提供

它是多类分类问题中输出层的首选，其中每个神经元对应于不同的类，并且您希望选择最有可能的类。

3.3：反向传播：神经学习的核心

反向传播是“误差的向后传播”的缩写，是一种有效计算网络中所有权重的损失函数梯度的方法。它由两个主要阶段组成：前向传递，输入数据通过网络生成输出，以及向后传递，将输出与目标值进行比较，并通过网络传播误差以更新权重。

反向传播的本质是微积分的链式法则，它用于通过乘以其后面层的梯度来计算每个权重的损失函数的梯度。这个过程揭示了每个权重对误差的贡献程度，为其调整提供了清晰的路径。

反向传播的链式法则可以表示如下：

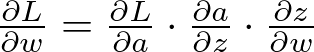
反向传播中的规则链 — 图片由作者提供

解释：

∂a/∂L 是损失函数到激活的梯度，
∂z/∂a 是激活函数与加权输入 z 的梯度，
∂w/∂z 是加权输入到权重 w 的梯度，
z 表示输入的加权总和，a 表示激活。

梯度下降：优化权重

梯度下降是一种优化算法，用于最小化神经网络中的损失函数。它的工作原理是将权重向损失最陡峭的方向迭代移动。在每次迭代中调整权重的量由学习率决定，学习率是控制步骤大小的超参数。

从数学上讲，梯度下降中的权重更新规则可以表示为：

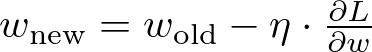
梯度下降公式 — 图片由作者提供

解释：

w-new 和 w-old 分别表示权重的更新（新）和当前（旧）值，
η是学习率，这是一个超参数，用于控制在负梯度方向上所采取的步骤的大小，
∂w/∂L 是重量损失函数的梯度。

在实践中，反向传播和梯度下降是同时进行的。反向传播计算网络中每个权重的梯度（误差的方向和大小），梯度下降使用此信息来更新权重以最大程度地减少损失。此迭代过程一直持续到模型收敛到损失最小化或满足条件的状态。

3.4：分步示例

让我们来探讨一个在简单神经网络中涉及反向传播和梯度下降的例子。这个神经网络将有一个隐藏层。我们将使用一个数据点进行一次训练迭代，以了解这些过程如何更新网络的权重。

网络结构：

Inputs: x1、x2（二维输入向量）
Hidden Layer: 2 个神经元，激活函数 f（z）=ReLU（z）=max（0，z）
Output Layer: 1 个神经元，激活函数 g（z）=σ（z）=1+e−z1（用于二元分类的 Sigmoid 函数）
Loss Function: 二元交叉熵损失。

前向通行证

给定输入 x1、x2、权重 w 和偏差 b，前向传递计算网络的输出。在隐藏层中激活 ReLU 并在输出层中激活 S 形的单个隐藏层网络的过程如下：

1：输入到隐藏层

设从输入到隐藏层的初始权重分别为 w11、w12、w21、w22，两个隐藏神经元的偏差分别为 b1、b2。

给定一个输入向量 [x1， x2]，隐藏层中每个神经元的加权和为：

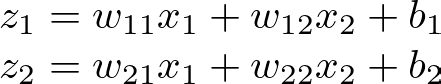
隐藏层加权总和 — 图片由作者提供

应用 ReLU 激活函数：

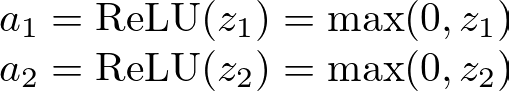
隐藏层 ReLU 激活 — 图片由作者提供

1.2：要输出的隐藏层：

设从隐藏层到输出神经元的权重为 w31、w32，偏差为 b3。

输出神经元的加权和为：

输出图层加权总和 — 图片由作者提供

将 Sigmoid 激活函数应用于输出：

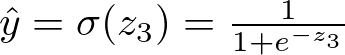
输出层 Sigmoid 激活 — 图片由作者提供

损失计算（二元交叉熵）：

交叉熵公式 — 图片由作者提供

向后传递（反向传播）：

现在事情变得有点复杂了，因为我们需要计算我们在前向传递中应用的公式的梯度。

输出层渐变

让我们从输出层开始。z3 的损失函数的导数为：

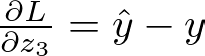
输出层激活梯度 — 图片由作者提供

输出层的权重和偏差损失梯度：

输出图层渐变 — 图片由作者提供

隐藏层渐变

隐藏层激活的损失梯度（应用链式法则）：

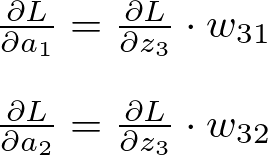
隐藏层激活梯度 — 图片由作者提供

关于隐藏层的权重和偏差的损失梯度：

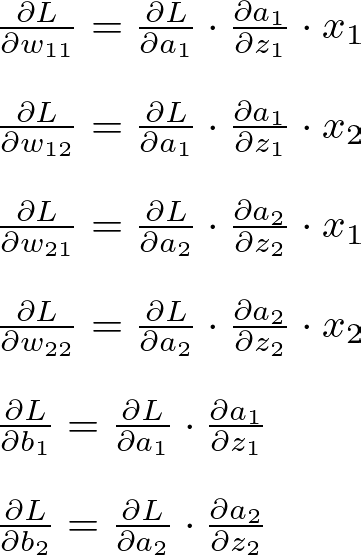
隐藏图层渐变 — 图片由作者提供

然后重复这些步骤，直到满足条件，例如最大纪元数。

3.5：改进

虽然梯度下降的基本思想很简单——朝着最能减少误差的方向迈出一小步——但已经对这种方法进行了一些调整和改进，以提高其效率和有效性。

随机梯度下降（SGD）

随机梯度下降（SGD）采用梯度下降的核心思想，但改变了方法，一次只使用一个训练示例来计算梯度并更新权重。这种方法类似于根据快速的个人观察做出决策，而不是等待收集每个人的意见。它可以使学习过程更快，因为模型更新更频繁，计算负担更小。

Adam (Adaptive Moment Estimation)（自适应矩估计）

Adam是Adaptive Moment Estimation的缩写，就像是SGD年轻活力的明智顾问。它采用根据数据梯度调整权重的概念，但对模型中的每个参数采用更复杂、更个性化的方法。Adam 结合了另外两个梯度下降改进 AdaGrad 和 RMSProp 的想法，根据梯度的第一个（平均值）和第二个（非中心方差）矩调整网络中每个权重的学习率。

4：实现神经网络

4.1：在 Python 中构建简单的神经网络

最后，让我们从头开始重新创建一个神经网络。为了提高可读性，我将代码分为 4 个部分：NeuralNetwork 类、Trainer 类和实现。

您可以在此 Jupyter Notebook 上找到完整代码。该笔记本包含一个微调奖励，可能会提高神经网络的性能：

NeuralNetwork 类
让我们从 NN 类开始，它定义了神经网络的架构：

import numpy as np

class NeuralNetwork:
    """
    A simple neural network with one hidden layer.

    Parameters:
    -----------
    input_size: int
        The number of input features
    hidden_size: int
        The number of neurons in the hidden layer
    output_size: int
        The number of neurons in the output layer
    loss_func: str
        The loss function to use. Options are 'mse' for mean squared error, 'log_loss' for logistic loss, and 'categorical_crossentropy' for categorical crossentropy.
    """
    def __init__(self, input_size, hidden_size, output_size, loss_func='mse'):
        self.input_size = input_size
        self.hidden_size = hidden_size
        self.output_size = output_size
        self.loss_func = loss_func
        
        # Initialize weights and biases
        self.weights1 = np.random.randn(self.input_size, self.hidden_size)
        self.bias1 = np.zeros((1, self.hidden_size))
        self.weights2 = np.random.randn(self.hidden_size, self.output_size)
        self.bias2 = np.zeros((1, self.output_size))

        # track loss
        self.train_loss = []
        self.test_loss = []
        
    def forward(self, X):
        """
        Perform forward propagation.
        
        Parameters:
        -----------
        X: numpy array
            The input data
        
        Returns:
        --------
        numpy array
            The predicted output
        """
        # Perform forward propagation
        self.z1 = np.dot(X, self.weights1) + self.bias1
        self.a1 = self.sigmoid(self.z1)
        self.z2 = np.dot(self.a1, self.weights2) + self.bias2
        if self.loss_func == 'categorical_crossentropy':
            self.a2 = self.softmax(self.z2)
        else:
            self.a2 = self.sigmoid(self.z2)
        return self.a2
    
    def backward(self, X, y, learning_rate):
        """
        Perform backpropagation.

        Parameters:
        -----------
        X: numpy array
            The input data
        y: numpy array
            The target output
        learning_rate: float
            The learning rate
        """
        # Perform backpropagation
        m = X.shape[0]
        
        # Calculate gradients
        if self.loss_func == 'mse':
            self.dz2 = self.a2 - y
        elif self.loss_func == 'log_loss':
            self.dz2 = -(y/self.a2 - (1-y)/(1-self.a2))
        elif self.loss_func == 'categorical_crossentropy':
            self.dz2 = self.a2 - y
        else:
            raise ValueError('Invalid loss function')
        
        self.dw2 = (1 / m) * np.dot(self.a1.T, self.dz2)
        self.db2 = (1 / m) * np.sum(self.dz2, axis=0, keepdims=True)
        self.dz1 = np.dot(self.dz2, self.weights2.T) * self.sigmoid_derivative(self.a1)
        self.dw1 = (1 / m) * np.dot(X.T, self.dz1)
        self.db1 = (1 / m) * np.sum(self.dz1, axis=0, keepdims=True)
        
        # Update weights and biases
        self.weights2 -= learning_rate * self.dw2
        self.bias2 -= learning_rate * self.db2
        self.weights1 -= learning_rate * self.dw1
        self.bias1 -= learning_rate * self.db1
        
    def sigmoid(self, x):
        """
        Sigmoid activation function.
        
        Parameters:
        -----------
        x: numpy array
            The input data
        
        Returns:
        --------
        numpy array
            The output of the sigmoid function
        """
        return 1 / (1 + np.exp(-x))
    
    def sigmoid_derivative(self, x):
        """
        Derivative of the sigmoid activation function.

        Parameters:
        -----------
        x: numpy array
            The input data
        
        Returns:
        --------
        numpy array
            The output of the derivative of the sigmoid function
        """
        return x * (1 - x)
    
    def softmax(self, x):
        """
        Softmax activation function.

        Parameters:
        -----------
        x: numpy array
            The input data
        
        Returns:
        --------
        numpy array
            The output of the softmax function
        """
        exps = np.exp(x - np.max(x, axis=1, keepdims=True))
        return exps/np.sum(exps, axis=1, keepdims=True)

Initialization 初始化

def __init__(self, input_size, hidden_size, output_size, loss_func='mse'):
    self.input_size = input_size
    self.hidden_size = hidden_size
    self.output_size = output_size
    self.loss_func = loss_func
    
    # Initialize weights and biases
    self.weights1 = np.random.randn(self.input_size, self.hidden_size)
    self.bias1 = np.zeros((1, self.hidden_size))
    self.weights2 = np.random.randn(self.hidden_size, self.output_size)
    self.bias2 = np.zeros((1, self.output_size))

    # track loss
    self.train_loss = []
    self.test_loss = []

该 __init__ 方法初始化 NeuralNetwork 类的新实例。它采用输入层（ input_size ）、隐藏层（ hidden_size ）和输出层（ output_size ）的大小作为参数，以及要使用的损失函数类型（ loss_func ），默认为均方误差（mse）。

在这种方法中，网络的权重和偏差被初始化。 weights1 将输入层连接到隐藏层，并将 weights2 隐藏层连接到输出层。偏差（ bias1 和 bias2 ）初始化为零数组。此初始化使用随机数作为权重以打破对称性，使用零作为偏差作为起点。

它还初始化两个列表， train_loss 以及 test_loss ，以分别跟踪训练和测试阶段的损失。

前向传播（ forward 方法）

def forward(self, X):
    # Perform forward propagation
    self.z1 = np.dot(X, self.weights1) + self.bias1
    self.a1 = self.sigmoid(self.z1)
    self.z2 = np.dot(self.a1, self.weights2) + self.bias2
    if self.loss_func == 'categorical_crossentropy':
        self.a2 = self.softmax(self.z2)
    else:
        self.a2 = self.sigmoid(self.z2)
    return self.a2

该 forward 方法获取输入数据 X 并将其传递到网络中。它计算加权和（ z1 ， z2 ），并将激活函数（sigmoid 或 softmax，取决于损失函数）应用于这些和以获得激活（ a1 ， a2 ）。

对于隐藏层，它始终使用 sigmoid 激活函数。对于输出层，如果损失函数为“categorical_crossentropy”，则使用 softmax，否则使用 sigmoid。sigmoid 和 softmax 之间的选择取决于任务的性质（二进制/多类分类）。

此方法返回网络的最终输出（ a2 ），可用于进行预测。

反向传播（ backward 方法）

def backward(self, X, y, learning_rate):
    # Perform backpropagation
    m = X.shape[0]
    
    # Calculate gradients
    if self.loss_func == 'mse':
        self.dz2 = self.a2 - y
    elif self.loss_func == 'log_loss':
        self.dz2 = -(y/self.a2 - (1-y)/(1-self.a2))
    elif self.loss_func == 'categorical_crossentropy':
        self.dz2 = self.a2 - y
    else:
        raise ValueError('Invalid loss function')
    
    self.dw2 = (1 / m) * np.dot(self.a1.T, self.dz2)
    self.db2 = (1 / m) * np.sum(self.dz2, axis=0, keepdims=True)
    self.dz1 = np.dot(self.dz2, self.weights2.T) * self.sigmoid_derivative(self.a1)
    self.dw1 = (1 / m) * np.dot(X.T, self.dz1)
    self.db1 = (1 / m) * np.sum(self.dz1, axis=0, keepdims=True)
    
    # Update weights and biases
    self.weights2 -= learning_rate * self.dw2
    self.bias2 -= learning_rate * self.db2
    self.weights1 -= learning_rate * self.dw1
    self.bias1 -= learning_rate * self.db1

该 backward 方法实现了反向传播算法，该算法用于根据预测输出与实际输出（）之间的误差更新网络中的权重和偏差 y 。
它使用链式法则计算权重和偏差（ dw2 ， db2 ， dw1 ， db1 ）的损失函数梯度。梯度表示需要调整多少权重和偏差以最小化误差。

学习率（ learning_rate ）控制在更新期间采取的步骤有多大。然后，该方法通过减去学习率及其各自梯度的乘积来更新权重和偏差。

根据所选的损失函数执行不同的梯度计算，说明了网络适应各种任务的灵活性。

激活函数（ *sigmoid* ， *sigmoid_derivative* 方法 *softmax* ）

def sigmoid(self, x):
    return 1 / (1 + np.exp(-x))

def sigmoid_derivative(self, x):
    return x * (1 - x)

def softmax(self, x):
    exps = np.exp(x - np.max(x, axis=1, keepdims=True))
    return exps/np.sum(exps, axis=1, keepdims=True)

sigmoid ：此方法实现 sigmoid 激活函数，该函数将输入值压缩到 0 和 1 之间的范围内。它对于二元分类问题特别有用。
sigmoid_derivative ：这计算了 sigmoid 函数的导数，在反向传播期间用于计算梯度。
softmax ：softmax 函数用于多类分类问题。它通过获取每个输出的指数，然后对这些值进行归一化，使它们的总和为 1，将来自网络的分数转换为概率。

**Trainer Class **

下面的代码介绍了一个 Trainer 旨在训练神经网络模型的类。它封装了进行训练所需的一切，包括执行训练周期（epoch）、计算损失以及通过基于损失的反向传播来调整模型的参数。

class Trainer:
    """
    A class to train a neural network.

    Parameters:
    -----------
    model: NeuralNetwork
        The neural network model to train
    loss_func: str
        The loss function to use. Options are 'mse' for mean squared error, 'log_loss' for logistic loss, and 'categorical_crossentropy' for categorical crossentropy.
    """
    def __init__(self, model, loss_func='mse'):
        self.model = model
        self.loss_func = loss_func
        self.train_loss = []
        self.test_loss = []

    def calculate_loss(self, y_true, y_pred):
        """
        Calculate the loss.

        Parameters:
        -----------
        y_true: numpy array
            The true output
        y_pred: numpy array
            The predicted output
        
        Returns:
        --------
        float
            The loss
        """
        if self.loss_func == 'mse':
            return np.mean((y_pred - y_true)**2)
        elif self.loss_func == 'log_loss':
            return -np.mean(y_true*np.log(y_pred) + (1-y_true)*np.log(1-y_pred))
        elif self.loss_func == 'categorical_crossentropy':
            return -np.mean(y_true*np.log(y_pred))
        else:
            raise ValueError('Invalid loss function')

    def train(self, X_train, y_train, X_test, y_test, epochs, learning_rate):
        """
        Train the neural network.

        Parameters:
        -----------
        X_train: numpy array
            The training input data
        y_train: numpy array
            The training target output
        X_test: numpy array
            The test input data
        y_test: numpy array
            The test target output
        epochs: int
            The number of epochs to train the model
        learning_rate: float
            The learning rate
        """
        for _ in range(epochs):
            self.model.forward(X_train)
            self.model.backward(X_train, y_train, learning_rate)
            train_loss = self.calculate_loss(y_train, self.model.a2)
            self.train_loss.append(train_loss)
            
            self.model.forward(X_test)
            test_loss = self.calculate_loss(y_test, self.model.a2)
            self.test_loss.append(test_loss)

以下是该类及其方法的详细细分：
类初始化（ *__init__* 方法）

def __init__(self, model, loss_func='mse'):
    self.model = model
    self.loss_func = loss_func
    self.train_loss = []
    self.test_loss = []

构造函数采用神经网络模型（ model ）和损失函数（ loss_func ）作为输入。如果未指定， loss_func 则默认为均方误差（mse）。

它初始化 train_loss 和 test_loss 列出以跟踪训练和测试阶段的损失值，从而允许监控模型随时间推移的性能。

计算损失（ *calculate_loss* 方法）

def calculate_loss(self, y_true, y_pred):
    if self.loss_func == 'mse':
        return np.mean((y_pred - y_true)**2)
    elif self.loss_func == 'log_loss':
        return -np.mean(y_true*np.log(y_pred) + (1-y_true)*np.log(1-y_pred))
    elif self.loss_func == 'categorical_crossentropy':
        return -np.mean(y_true*np.log(y_pred))
    else:
        raise ValueError('Invalid loss function')

此方法使用指定的损失函数计算预测输出（ y_pred ）和真实输出（ y_true ）之间的损失。这对于评估模型的性能和执行反向传播至关重要。

该方法支持三种类型的损失函数：

均方误差（’mse’）：用于回归任务，计算预测值和真实值之间差值的平方平均值。
逻辑损失（’log_loss’）：适用于二元分类问题，使用对数似然法计算损失。
分类交叉熵（’categorical_crossentropy’）：非常适合多类分类任务，用于测量真实标签和预测之间的差异。

如果提供了无效的损失函数，则会引发 ValueError .

训练模型（ train 方法）

def train(self, X_train, y_train, X_test, y_test, epochs, learning_rate):
    for _ in range(epochs):
        self.model.forward(X_train)
        self.model.backward(X_train, y_train, learning_rate)
        train_loss = self.calculate_loss(y_train, self.model.a2)
        self.train_loss.append(train_loss)
        
        self.model.forward(X_test)
        test_loss = self.calculate_loss(y_test, self.model.a2)
        self.test_loss.append(test_loss)

该 train 方法使用训练（ X_train ， y_train ）和测试数据集（ X_test ， y_test ）管理指定数量的 epoch 的训练过程。它还需要一个 learning_rate 参数，该参数会影响反向传播期间参数更新中的步长。

对于每个 epoch（训练周期），该方法执行以下步骤：

训练数据的前向传递：它使用模型 forward 的方法来计算训练数据的预测输出。
向后传递（参数更新）：它使用训练数据和标签（ y_train ） learning_rate 应用模型 backward 的方法，并根据从损失计算出的梯度更新模型的权重和偏差。
计算训练损失：使用带有训练标签和预测 calculate_loss 的方法计算训练损失。然后，将此损失附加到 train_loss 列表中进行监视。
前向传递测试数据：同样，该方法计算测试数据的预测，以评估模型在看不见的数据上的性能。
计算测试损失：它使用测试标签和预测计算测试损失，并将此损失追加到 test_loss 列表中。

实现

在本节中，我将概述加载数据集、准备训练以及使用它来训练神经网络以执行分类任务的完整过程。该过程涉及数据预处理、模型创建、训练和评估。

对于此任务，我们将使用开源（BSD-3 许可证）sci-kit 学习库中的 digits 数据集。单击此处了解有关 Sci-Kit Learn 的更多信息。

# Load the digits dataset
digits = load_digits()

# Preprocess the dataset
scaler = MinMaxScaler()
X = scaler.fit_transform(digits.data)
y = digits.target

# One-hot encode the target output
encoder = OneHotEncoder(sparse=False)
y_onehot = encoder.fit_transform(y.reshape(-1, 1))

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y_onehot, test_size=0.2, random_state=42)

# Create an instance of the NeuralNetwork class
input_size = X.shape[1]
hidden_size = 64
output_size = len(np.unique(y))
loss_func = 'categorical_crossentropy'
epochs = 1000
learning_rate = 0.1

nn = NeuralNetwork(input_size, hidden_size, output_size, loss_func)

trainer = Trainer(nn, loss_func)
trainer.train(X_train, y_train, X_test, y_test, epochs, learning_rate)

# Convert y_test from one-hot encoding to labels
y_test_labels = np.argmax(y_test, axis=1)

# Evaluate the performance of the neural network
predictions = np.argmax(nn.forward(X_test), axis=1)
accuracy = np.mean(predictions == y_test_labels)
print(f"Accuracy: {accuracy:.2%}")

让我们来看看每个步骤：

加载数据集

1 2	# Load the digits dataset digits = load_digits()

数字数据集前 10 张图像 — 图片由作者提供

这里使用的数据集是 digits 数据集，通常用于涉及识别手写数字的分类任务。

预处理数据集

# Preprocess the dataset
scaler = MinMaxScaler()
X = scaler.fit_transform(digits.data)
y = digits.target

使用 MinMaxScaler .这是一个常见的预处理步骤，以确保所有输入特征具有相同的比例，这可以帮助神经网络更有效地学习。

缩放后的要素存储在中 X ，目标标注（每个图像所代表的数字）存储在 y 中。

对目标输出进行One-hot编码*

1
2
3

# One-hot encode the target output
encoder = OneHotEncoder(sparse=False)
y_onehot = encoder.fit_transform(y.reshape(-1, 1))

由于这是一个具有多个类的分类任务，因此目标标签是使用 OneHotEncoder .One-hot 编码将分类目标数据转换为神经网络更易于理解和使用的格式，尤其是对于分类任务。

拆分数据集

1 2	# Split the dataset into training and testing sets X_train, X_test, y_train, y_test = train_test_split(X, y_onehot, test_size=0.2, random_state=42)

数据集使用 train_test_split 分为训练集和测试集，其中 80% 的数据用于训练，20% 用于测试。这种拆分允许在数据的一部分上训练模型，然后在单独的、看不见的部分上评估其性能，以检查其泛化程度。

创建 NeuralNetwork 类的实例*

# Create an instance of the NeuralNetwork class
input_size = X.shape[1]
hidden_size = 64
output_size = len(np.unique(y))
loss_func = 'categorical_crossentropy'
epochs = 1000
learning_rate = 0.1

nn = NeuralNetwork(input_size, hidden_size, output_size, loss_func)

使用指定的输入大小（特征数）、隐藏大小（隐藏层中的神经元数）、输出大小（唯一标签数）和要使用的损失函数创建神经网络实例。输入大小与要素数量匹配，输出大小与唯一目标类的数量匹配，并选择隐藏图层大小。

训练神经网络

1 2	trainer = Trainer(nn, loss_func) trainer.train(X_train, y_train, X_test, y_test, epochs, learning_rate)

使用神经网络和损失函数创建 Trainer 类的实例。然后，使用训练和测试数据集以及指定的 epoch 数和学习率调用该 train 方法。此过程迭代调整神经网络的权重和偏差，以最小化损失函数，使用训练数据进行学习，使用测试数据进行验证。

评估性能

# Convert y_test from one-hot encoding to labels
y_test_labels = np.argmax(y_test, axis=1)

# Evaluate the performance of the neural network
predictions = np.argmax(nn.forward(X_test), axis=1)
accuracy = np.mean(predictions == y_test_labels)
print(f"Accuracy: {accuracy:.2%}")

训练后，在测试集上评估模型的性能。由于目标是 one-hot 编码的， np.argmax 因此用于将 one-hot 编码的预测转换回标签形式。模型的准确率是通过将这些预测标签与实际标签（ y_test_labels ）进行比较来计算的，然后打印出来。

现在，这段代码缺少一些我们讨论过的激活函数、SGD 或 Adam Optimizer 等改进。我把它留给你，通过用你的代码填补空白，使这个代码成为你自己的。这样，您将真正掌握神经网络。

4.2：利用库实现神经网络（TensorFlow）

嗯，那很多！幸运的是，我们不需要每次使用神经网络时都编写这么长的代码。我们可以利用 Tensorflow 和 PyTorch 等库，它们将以最少的代码为我们创建深度学习模型。在此示例中，我们将创建并解释在数字数据集上训练神经网络的 TensorFlow 版本，类似于前面描述的过程。

和以前一样，让我们首先导入所需的库和数据集，然后以与之前相同的方式对其进行预处理。

import tensorflow as tf
from sklearn.datasets import load_digits
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import MinMaxScaler, OneHotEncoder

# Load the digits dataset
digits = load_digits()

# Scale the features to a range between 0 and 1
scaler = MinMaxScaler()
X_scaled = scaler.fit_transform(digits.data)

# One-hot encode the target labels
encoder = OneHotEncoder(sparse=False)
y_onehot = encoder.fit_transform(digits.target.reshape(-1, 1))

# Split the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X_scaled, y_onehot, test_size=0.2, random_state=42)

其次，让我们构建 NN：

# Define the model architecture
model = tf.keras.models.Sequential([
    tf.keras.layers.Dense(64, activation='relu', input_shape=(X_train.shape[1],)),
    tf.keras.layers.Dense(len(np.unique(digits.target)), activation='softmax')
])

在这里，将创建一个 Sequential 模型，指示层的线性堆栈。

第一层是具有 64 个单元（神经元）和 ReLU 激活的密集连接层。它需要来自形状的输入，该形状 (X_train.shape[1],) 与数据集中的要素数量相匹配。

输出层具有多个单位，等于唯一目标类的数量，并使用 softmax 激活函数输出每个类的概率。

# Compile the model
model.compile(optimizer='adam',
              loss='categorical_crossentropy',
              metrics=['accuracy'])

该模型以Adam优化器和分类交叉熵为损失函数进行编译，适用于多类分类任务。准确性被指定为评估指标。

最后，让我们训练和评估 NN 的性能：

# Train the model
history = model.fit(X_train, y_train, epochs=1000, validation_data=(X_test, y_test), verbose=2)

# Evaluate the model on the test set
test_loss, test_accuracy = model.evaluate(X_test, y_test, verbose=2)
print(f"Test accuracy: {test_accuracy:.2%}")

使用具有 1000 个 epoch fit 的方法对模型进行训练，并将测试集用作验证数据。 verbose=2 表示将打印每个 epoch 一行用于日志记录。

最后，使用该 evaluate 方法在测试集上评估模型的性能，并打印测试精度。

5：挑战

5.1：克服过拟合

过度拟合就像神经网络变得有点过于沉迷于其训练数据，拾取所有微小的细节和噪音，以至于它难以处理新的、看不见的数据。这就像通过逐字背诵教科书来努力学习考试，但随后却无法将所学知识应用于任何措辞不同的问题。这个问题可能会阻碍模型在现实世界中表现良好的能力，在现实情况下，能够将其学到的知识概括或应用于新场景是关键。幸运的是，有几种聪明的技术可以帮助防止或减少过度拟合，使我们的模型更加通用，并为现实世界做好准备。让我们来看看其中的一些，但现在不要担心掌握所有这些，因为我将在另一篇文章中介绍反过拟合技术。

Dropout: 这就像在训练过程中随机关闭网络中的一些神经元一样。它阻止了神经元过于依赖彼此，迫使网络学习更强大的特征，而不仅仅是依靠一组特定的神经元来做出预测。

提前停止

这涉及观察模型在训练时在验证集（单独的数据块）上的表现。如果模型在这个集合上开始表现得更糟，则表明它开始过度拟合，是时候停止训练了。

使用验证集

将数据分为三组（训练、验证和测试）有助于密切关注过度拟合。验证集用于调整模型并选择最佳版本，而测试集则对模型的运行情况进行公平评估。

简化模型

有时，少即是多。如果模型过于复杂，它可能会开始从训练数据中拾取噪声。通过选择更简单的模型或减少层数，我们可以降低过拟合的风险。

当您尝试 NN 时，您会发现微调和解决过拟合将在 NN 的性能中发挥关键作用。确保你掌握了反过拟合技术，对于一个成功的数据科学家来说，这是必须的。由于它的重要性，我将用一整篇文章来介绍这些技术，以确保您可以微调最佳神经网络并保证您的项目具有最佳性能。

6：结论

潜入神经网络的世界，让我们看到了这些模型在人工智能领域所拥有的不可思议的潜力。从基础开始，比如神经网络如何使用加权和激活函数来处理信息，我们已经看到了反向传播和梯度下降等技术如何使它们能够从数据中学习。特别是在图像识别等领域，我们亲眼目睹了神经网络如何解决复杂的挑战并推动技术向前发展。

展望未来，很明显，我们才刚刚开始一段名为“深度学习”的漫长旅程。在接下来的文章中，我们将讨论更高级的深度学习架构、微调方法等等！

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/花生_TL007/article/detail/465666

神经网络背后的数学原理

1：基础知识

1.1：什么是神经网络？

1.2：神经网络的类型

2：神经网络的架构

2.1：神经元的结构

2.2：图层

2.3：层在学习中的作用

3：神经网络的数学

3.1：加权总和

3.2：激活函数

3.3：反向传播：神经学习的核心

3.4：分步示例

3.5：改进

4：实现神经网络

4.1：在 Python 中构建简单的神经网络

4.2：利用库实现神经网络 （TensorFlow）

5：挑战

5.1：克服过拟合

6：结论

4.2：利用库实现神经网络（TensorFlow）