Course3-Week3-强化学习_吴恩达强化学习学习笔记

Course3-Week3-强化学习

• 笔记主要参考B站视频“(强推|双字)2022吴恩达机器学习Deeplearning.ai课程”。
• 该课程在Course上的页面：Machine Learning 专项课程
• 课程资料：“UP主提供资料(Github)”、或者“我的下载(百度网盘)”。
• 本篇笔记对应课程 Course3-Week3（下图中深紫色）。

---

1. 强化学习的问题引入

1.1 什么是强化学习

  “强化学习(reinforcement learning)”已经被应用于直升机控制，可以让其做“倒飞”等各种特技动作(aerobatic maneuvers)，如上图。显然我们不可能使用“有监督学习”来控制直升机，因为整个飞行空间是连续的，标签数据空间会非常庞大进而制造困难大。而“强化学习”的关键思想在于，并不告诉算法对于每个输入的正确输出(事实上也做不到)，而是指定一个“奖励函数(reward function)”，来告诉算法执行的结果如何，“强化学习”算法的工作就是自动找出“最大化奖励”的动作。也就是，在训练时只给出“奖励函数(reward function)”，而不是最佳动作。这可以在设计系统时具有更多的灵活性。比如对于“直升机控制”来说，可以设置奖励为：

1. 正向反馈(positive reward)：直升机飞行稳定时，+1分。
2. 负向反馈(negative reward)：直升机坠毁，-1000分。

“强化学习”的应用场景有：

1. 机器人控制。比如直升机特技飞行、机器狗跨越障碍等。
2. 工厂优化。如何安排工厂中流程来最大限度的提升 吞吐量/效率。
3. 金融(股票)交易。比如要想在10天内抛售100万手股票，如何效益最大化的完成股票交易。
4. 玩游戏。比如挑起、国际象棋、纸牌、电子游戏等等。

  尽管“强化学习”不如“有监督学习”应用广泛，目前尚未在商业界取得广泛应用，但也是机器学习算法的“支柱”之一。下面是目前“强化学习”的一些缺点：

1. 很多研究成果都是针对模拟环境的，而针对“实际机器人”的“强化学习”要困难的多。
2. 应用场景少。相比于“有/无监督学习”，“强化学习”的应用场景很少，目前大多数局限在机器人控制领域。

注：“强化学习”既不是“有监督学习”，也不是“无监督学习”。

1.2 强化学习示例

本节介绍几个强化学习的示例，其中“火星探测器”会在第二节反复提及。

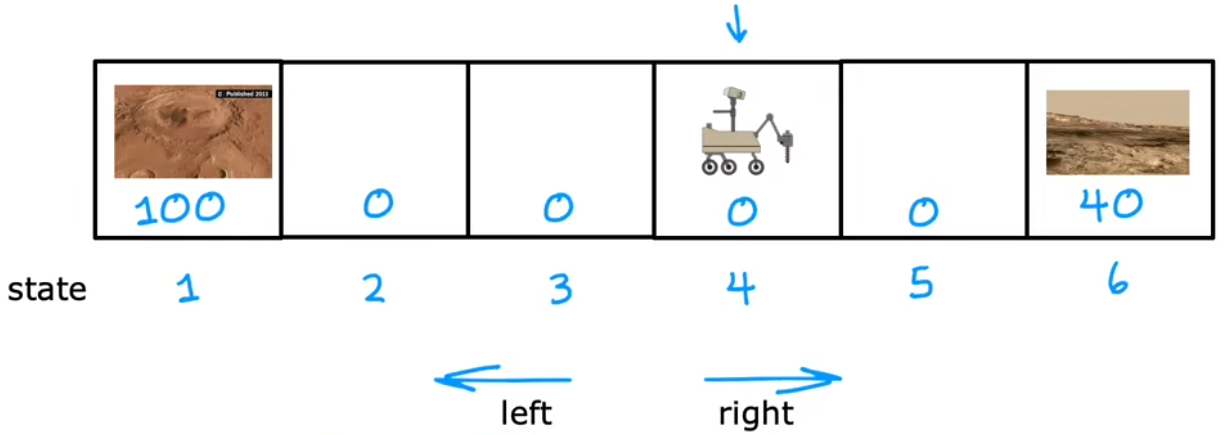
【问题1】“火星探测器”：找出火星车在每个状态应该执行的最佳动作，直到到达“状态1”或“状态6”。

• 状态(state)：假设有6个状态。每个状态可以认为是不同的地点，“状态1”或“状态6”为“任务终点(terminal state)”。下图中火星车的起始位置为“状态4”。
• 动作(action)：每个状态都可以执行“向左”、“向右”两种状态。
• 奖励(reward)：到达“状态1”奖励100、到达“状态6”奖励40、其他状态奖励为0。
• 折扣因子：$\gamma =0.5$

【问题2】“直升机控制”：根据当前状态自动选择动作，以保证直升机的平稳运行。

• 状态：直升机的空间位置。
• 动作：如何移动直升机遥控上的控制杆。
• 奖励：飞行平稳+1，坠毁-1000。
• 折扣因子：$\gamma =0.99$

【问题3】“国际象棋”【简化描述】：根据棋盘上所有棋子的位置，自动选择最佳的下一步棋。

• 状态：棋盘上所有棋子的位置。
• 动作：可能的移动方式。
• 奖励：赢了+1，胜负未分0，输了-1。
• 折扣因子：$\gamma =0.995$

【问题4】“登月器”：控制登月器成功实现软着陆。

• 具体介绍参照3.1节。

1.3 数学符号

下面是本周会用到的一些数学符号，简单看一眼，用到的时候来查就行。

• $s$ / $\vec{s}$：机器人的当前状态。
• $a$ / $\vec{a}$：机器人在当前状态执行的动作。
• $R(s)$：机器人在当前状态得到的奖励。
• $s^{\prime }$：机器人执行动作 $a$ 后进入的的下一状态。
• $a^{\prime }$：机器人在下一状态执行的动作。
• $\gamma$：0~1之间，奖励的折扣因子(discount factor)。很多算法会定义为0.9左右，本周默认 $\gamma =0.5$。
• $\pi (s)=a$：强化学习的策略，表示在“状态$s$”下应该执行的“最佳动作$a$”。
• $p$：0~1之间，表示机器人执行动作后，没有到达预期状态，反而由于某些随机因素到达相反状态的概率。

强化学习四大核心要素：当前状态、动作、奖励、下一状态。

注：第3节的“连续状态空间”会涉及到“向量”表示，上述只给出了“状态”和“动作”的向量形式，其余省略见上下文即可。

2. 离散状态空间的强化学习

本节通过一个简单的案例——“火星探测器”，来介绍“强化学习”中的核心数学公式和关键思想。

2.1 回报

  本小节来介绍强化学习的“回报”。强化学习的“回报(return)”是每一步所获得的 “奖励(reward)”的加权和，权重就是步数幂次的“折扣因子 $\gamma$”，“奖励”显然取决于每一次的“动作(action)”。比如下面从“状态1”不断执行动作，最终到达任务终点“状态n”，回报为：
$$\text{Return}=R_1+\gamma R_2+{\gamma }^2{R}_3+...+{\gamma }^{n-1}{R}_n(\text{terminal state})$$

若系统中出现“负奖励”，算法会尽可能的推迟该“负奖励”。折扣因子 $\gamma$ 越大，表示有“耐心”走向更远的“大奖励”。下图给出了折扣因子对最佳策略(黄色箭头)的影响，可以发现 $\gamma$ 较大时，状态5的最佳策略会是更远处的“大奖励”。

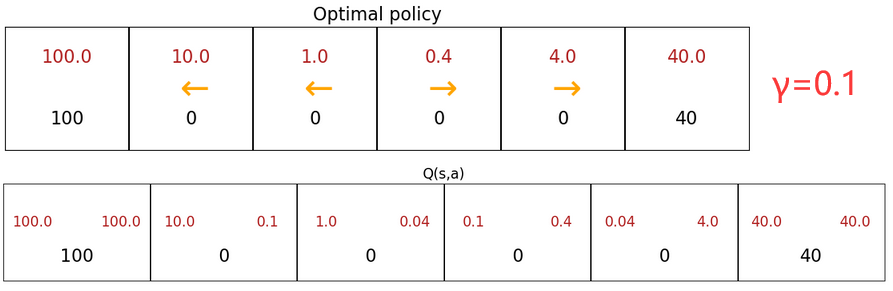
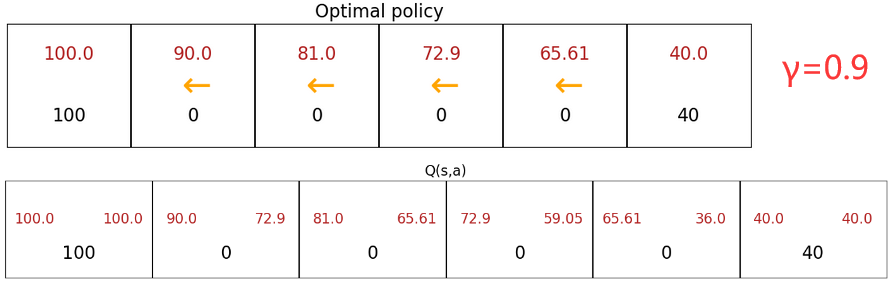
2.2 策略

  本节介绍强化学习如何选择“动作”，也就是强化学习算法的“策略”。“策略 $\pi$ (policy/controler)”是一个“状态”到“动作”的映射函数，表示在“状态$s$”下，为了“最大化回报”所应该执行的“最佳动作$a$”：
$$\pi (s)=a$$

上述决策过程被称为“马尔可夫决策过程(Markov Decision Process, MDP)”。“马尔可夫决策过程”是指未来只取决于当前状态，而不取决于任何之前的状态。

2.3 状态-动作价值函数

  整个强化学习最关键的一点就是计算“状态-动作价值函数(state-action value function)”，也称为$Q$函数、$Q^{\ast }$、最优$Q$函数(optimal Q function)。“状态-动作价值函数”就是在 “当前状态$s$” 下，执行 “某动作$a$” 后所能获得的“最大回报”。也就是说，“某动作$a$”不一定是当前状态的最佳动作，但执行 $a$ 之后会一直执行最佳动作($\gamma =0.5$)：

$$Q(s,a)=\max (\text{Return})\text{at}s\text{after}a$$

显然，在计算出所有状态下所有动作的 $Q$ 取值后，在每个状态只需选取 $Q$ 取值较大的“动作”，就是“最佳动作$\pi (s)=a$”。比如上述在“状态4”，因为 $Q(4,\leftarrow )>Q(4,\to )$，所以在“状态4”应该执行最佳动作 “向左$\leftarrow$”。比如上图3-3-3中($\gamma =0.5$)：
$$\begin{gathered} \text{Example 1 :}Q(2,\to )=R(2)+0.5\underset{a^{\prime }}{\max }Q(3,a^{\prime })=0+0.5\cdot 25=12.5 \\ \text{Example 2 :}Q(4,\leftarrow )=R(4)+0.5\underset{a^{\prime }}{\max }Q(3,a^{\prime })=0+0.5\cdot 25=12.5 \end{gathered}$$

2.4 贝尔曼方程

  将前几个小节的内容总结一下，就可以给出 $Q(s,a)$ 的计算公式——“贝尔曼方程(Bellman Equation)”，也就是在 状态$s$ 执行 动作$a$ 的最大回报=“即时奖励(immediate reward)”+下一状态的最大回报：
$$\text{Bellman Equation :}Q(s,a)=R(s)+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })$$

• $s$：当前状态。
• $a$：在当前状态执行的动作。
• $R(s)$：在当前状态得到的即时奖励。
• $s^{\prime }$：执行动作 $a$ 后进入的的下一状态。
• $a^{\prime }$：在下一状态 $s^{\prime }$ 执行的动作。
• $\gamma$：折扣因子。

2.5 随机环境(可选)

  本节介绍“随机马尔可夫决策过程(Stochastic Markov Decision Processes)”。和前面内容的区别是，实际中机器并不总是可靠，比如命令“火星车”从“状态3”执行“动作向左”，大多数情况都会如预期到达“状态2”，但是也可能因为岩石滑坡、沙暴、车轮打滑等小概率随机事件，导致其到达“状态4”。这种情况下，我们就需要定义“出错概率$p$”，来描述到达相反状态的概率。此时，由于整个过程是随机的，我们就不能单纯地追求“最大化回报”，而是要追求“最大化回报的期望”。于是“随机环境”下的“贝尔曼方程”更改为：
$$\text{(Stochastic) Bellman Equation :}Q(s,a)=R(s)+\gamma E\left[\underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })\right]$$

老师在视频中给出的求解期望的方法时暴力穷举，不断模拟出所有的可能，最后用平均值表示期望。但显然还有更聪明的方法没介绍。下面是在“jupyter notebook”中的仿真，说明了“出错概率”对最佳决策的影响：

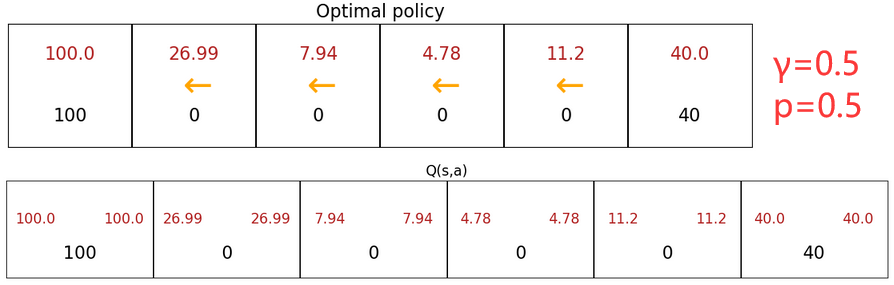
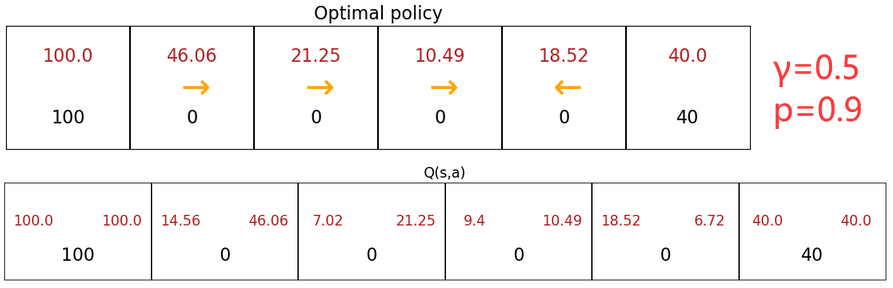
• “出错概率”的引入，会减小所有的回报。
• 【上左图】较小的“出错概率”不会改变最佳策略。
• 【上右图】较大的“出错概率”会使得最佳策略完全相反，相当于反向操作火星车。
• 【上中图】随机越接近0.5，火星车的移动越趋于随机(不受控制)。$p=0.5$ 时不存在最佳策略，因为指定火星车向哪走都一样，可以看到每个状态的Q函数完全相同。这种情况形象来说就是“那还玩个集贸啊？”

本节 Quiz：

1. You are using reinforcement learning to control a four legged robot. The position of the robot would be its _____?
   √ state
   × reward
   × action
   × return

2. You are controlling a Mars rover. You will be very very happy if it gets to state 1 (significant scientific discovery), slightly happy if it gets to state 2 (small scientific discovery), and unhappy if it gets to state 3 (rover is permanently damaged). To reflect this, choose a reward function so that:
   × R(1)< R(2)< R(3), where R(1) and R(2) are negative and R(3) is positive.
   √ R(1)> R(2)> R(3), where R(1) and R(2) are positive and R(3) is negative.
   × R(1)> R(2)> R(3), where R(1), R(2) and R(3) are negative.
   × R(1)> R(2)> R(3), where R(1), R(2) and R(3) are positive.

3. You are using reinforcement learning to fly a helicopter. Using a discount factor of 0.75, your helicopter starts in some state and receives rewards -100 on the first step, -100 on the second step, and 1000 on the third and final step (where it has reached a terminal state). What is the return?
   √ $-100-0.75\ast 100+0.75^2\ast 1000$
   × $-0.25\ast 100-0.25^2\ast 100+0.25^3\ast 1000$
   × $-100-0.25\ast 100+0.25^2\ast 1000$
   × $-0.75\ast 100-0.75^2\ast 100+0.75\ast 3\ast 1000$

4. Which of the fllowing accurately describes the state-action value function $Q(s,a)$?
   √ It is the return if you start from state $s$, take action $a$ (once), then behave optimally after that.
   × It is the return if you start from state $s$ and repeatedly take action $a$.
   × It is the return if you start from state $s$ and behave optimally.
   × It is the immediate reward if you start from state $s$ and take action $a$ (once).

5. You are controlling a robot that has 3 actions: $\leftarrow$(left), $\to$(right) and STOP. From a given state $s$, you have computed $Q(s,\leftarrow )=-10$, $Q(s,\to )=-20$, $Q(s,\text{STOP})=0$. What is the optimal action to take in state $s$?
   √ STOP
   × ←(left)
   × →(right)
   × Impossible to tell

3. 连续状态空间的强化学习

  之前我们介绍的场景只有6个状态，但很多实际应用的状态空间是连续的，于是状态的数量会非常大。此时我们就不可能手算 $Q$ 函数，而是使用神经网络来进行拟合(DQN算法)。下面就来介绍。

3.1 问题示例——登月器

  很多机器人控制的实际应用都有连续的状态空间。在之前的火星车问题中，我们将问题简化成6个状态，每个状态表示一个地点。但实际上我们想做的是控制火星车在地面上的移动，所以我们应该俯瞰火星车，将地面看成二维坐标，火星车的状态应该包括：位置$[x,y]$(二维坐标)、角度$\theta$、运动速度$[\dot{x},\dot{y}]$(两个方向的速度)、偏转速度$\dot{\theta }$共6个变量：
$$\vec{s}=[x,y,\theta ,\dot{x},\dot{y},\dot{\theta }{]}^T$$

另外，火星车的移动可以看成是二维平面的运动，而直升机的运动则是在三维空间的运动。于是直升机的状态应该包括：位置$[x,y,z]$、姿态信息$[\varphi ,\theta ,\omega ]$、位置变化速度$[\dot{x},\dot{y},\dot{z}]$、姿态变化的角速度$[\dot{\varphi },\dot{\theta },\dot{\omega }]$共12个变量：
$$\vec{s}=[x,y,z,\varphi ,\theta ,\omega ,\dot{x},\dot{y},\dot{z},\dot{\varphi },\dot{\theta },\dot{\omega }{]}^T$$

注：“姿态信息”的三维向量分别表示滚动(roll)、俯仰(pitch)、偏航(yaw)的角度，可以唯一确定刚体的姿态。

于是我们对“火星车探测”问题进行改进，来使用“登月器”这个二维连续空间问题进行举例。下面是问题介绍：

【问题1】“登月器”：控制登月器的运动，使其成功“立着”降落在两个黄旗之间(如下图)。

• 状态：是二维平面的小游戏，登月器的状态包括8种变量 $\vec{s}=[x,y,\dot{x},\dot{y},\theta ,\dot{\theta },l,r{]}^T$。

1. $[x,y]$：连续取值，表示登月器的二维坐标。
2. $\dot{x},\dot{y}$：连续取值，表示登月器在两个方向的速度。
3. $\theta$：连续取值，表示登月器的偏转角度。
4. $\dot{\theta }$：连续取值，表示登月器的偏转速度。
5. $[l,r]$：二进制取值，分别表示左、右支撑脚是否着地。帮助确认登月器是否为“倒栽葱”或者“躺着”着陆的。

• 动作：包括四个动作，什么都不做/向左点火/向右点火/向下点火。

1. 什么都不做(nothing)，登月器由于重力自然下坠。
2. 向左点火(fire left)，点燃左推进器，登月器向右移动。
3. 向右点火(fire right)，点燃右推进器，登月器向左移动。
4. 向下点火(fire main)，点燃主推进器，减缓登月器的下降速度。

• 奖励：考虑到整个着陆过程，定义以下7种奖励。前4个都是降落后判定，后3个是降落过程中持续判定。

1. 【+100~+140】别管是“立着”/“倒栽葱”/“躺着”，只要到达两黄旗之间就给奖励。离中心越近奖励越多。
2. 【-100】不管降落在哪里，只要不是“立着”降落，就判定为“坠毁”给惩罚。
3. 【+100】不管降落在哪里，只要成功实现“立着”降落(软着陆)就给奖励。
4. 【+10】不管降落在哪里，只要有一个支撑腿着地，就+10；两个就+20。
5. 【额外奖励】降落过程中，水平方向离两黄旗中心越近就给一点小奖励。
6. 【-0.3】为了节省燃料，每点燃一次主推进器(向下点火)，就给一点惩罚。
7. 【-0.03】为了节省燃料，每点燃一次左/右推进器，就给一点惩罚。

• 折扣因子：对于登月器来说，通常会令折扣因子较大，如$\gamma =0.985$。

上述奖励函数算是一个“中等复杂”的定义，花时间仔细定义“奖励”是合理的。因为即使看上去有点复杂，也比手动确定每个状态的最佳动作要简单许多。

3.2 DQN算法：拟合Q函数

  在上一大节的介绍中，$Q$函数对于最佳动作的选择至关重要。对于离散状态空间来说，可以手动计算甚至穷举；但对于连续状态空间来说，$Q$函数取值连续且几乎没有显式表达式，于是需要训练神经网络来拟合$Q$函数。也就是根据输入 $(\vec{s},\vec{a})$，计算输出 $Q(\vec{s},\vec{a})$，神经网络的结构如下：

• 输入层：12维向量，包括状态向量 $\vec{s}$ (长度为9) + 动作向量 $\vec{a}$ (4个动作的独热码)。
• 中间层：不妨定义两个中间层，每个中间层都有64个神经元。
• 输出层：Q函数的输出，也就是在 状态$\vec{s}$ 下采取 动作$\vec{a}$ 所能得到的最大回报。

注意：神经网络最开始的输出“y”并没有什么意义，只是随机初始化的参数。

那如何得到最开始的训练集呢？答案是利用神经网络的初始化参数。比如在某个时刻 $i$ 可以得到下面所示的“四要素” $({\vec{s}}^{(i)},{\vec{a}}^{(i)},R({\vec{s}}^{(i)}),{\vec{s}}^{\prime (i)})$，根据“四要素”可以直接得到是神经网络的输入 ${\vec{x}}^{(i)}$；而由于神经网络有随机初始化参数，所以可以计算出在下一状态 ${\vec{s}}^{\prime (i)}$ 下所有的动作的$Q$值，选出最大的便可以计算出神经网络的输出 $y^{(i)}$。于是就计算出来单个训练样本 $({\vec{x}}^{(i)},y^{(i)})$。不断重复这个过程(比如10000次)，便可得到大量的训练集：
( s ⃗ ( i ) , a ⃗ ( i ) , R ( s ⃗ ( i ) ) , s ⃗ ′ ( i ) )    ⟶ { x ⃗ ( i ) = ( s ⃗ ( i ) , a ⃗ ( i ) ) y ( i ) = R ( s ⃗ ( i ) ) + γ    max ⁡ a ⃗ ′ Q ( s ⃗ ′ ( i ) , a ⃗ ′ ) ⏟ Neural Network

$$\begin{aligned} (\vec{s}^{(i)},\vec{a}^{(i)},R(\vec{s}^{(i)}),\vec{s}'^{(i)})\;\longrightarrow \left\{\begin{aligned} & \vec{x}^{(i)}=(\vec{s}^{(i)}, \vec{a}^{(i)})\\ & y^{(i)} = R(\vec{s}^{(i)}) + \gamma\;\max_{\vec{a}'}\underbrace{Q(\vec{s}'^{(i)},\vec{a}')}_{\text{Neural Network}} \end{aligned}$$ \right. \end{aligned} (s (i),a (i),R(s (i)),s ′(i))⟶⎩ ⎨ ⎧​​x (i)=(s (i),a (i))y(i)=R(s (i))+γa ′max​Neural Network Q(s ′(i),a ′)​​​​

和前面“有监督学习”的神经网络不同的地方在于，“强化学习”的神经网络迭代更新一次需要使用两次神经网络。一次用于计算训练样本，一次用于更新参数。这个训练过程虽然看起来优点玄学，但能逐渐迭代出理想参数，但显然比“有监督学习”更慢。

具体是算法如下：

完整的DQN算法框架(Deep Q-Network)：

1. 初始化神经网络参数，作为Q函数的拟合。
2. 不断重复{
     1. 计算“四要素”。采取动作，计算得到10000个样本 $(\vec{s},\vec{a},R(\vec{s}),{\vec{s}}^{\prime })$。(Replay Buffer)
     2. 训练神经网络，迭代设定次数{
       1. 计算训练集。利用神经网络计算所有训练样本 $\vec{x}=(\vec{s},\vec{a})$、$y=R(\vec{s})+\gamma {\max }_{{\vec{a}}^{\prime }}Q({\vec{s}}^{\prime },{\vec{a}}^{\prime })$。
       2. 训练神经网络参数。使新的神经网络 $Q_{new}\approx y$。
     }
     3. 更新神经网络参数，$Q=Q_{new}$。
   }

3.3 算法改进：改进的神经网络架构

  我们使用神经网络来拟合 $Q(\vec{s},\vec{a})$。但在上一节中，对于每个状态 $\vec{s}$，我们都需要推理4次来逐个计算所有动作对应的$Q$值，并挑出最大值。这显然很麻烦，我们可以省略这一重复性的工作，直接令神经网络输出当前状态 $\vec{s}$ 下所有动作对应的$Q$值，此时我们推理1次便可以得到当前状态 $\vec{s}$ 所有的Q值：

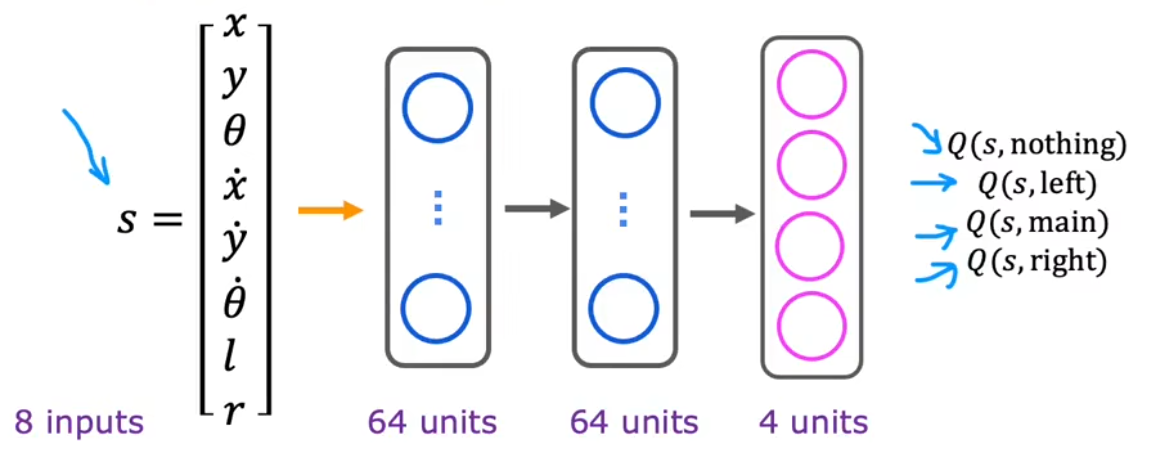
按照上面这种结构改进，会使得神经网络更加高效。

3.4 算法改进：$\epsilon$-贪婪策略、小批量、软更新

而对于算法我们也有一些改进的小技巧(黑色加粗)，下面来一一介绍：

完整的DQN算法框架(Deep Q-Network)：

1. 初始化神经网络参数，作为Q函数的拟合。
2. 不断重复{
     1. 计算“四要素”。使用“$\epsilon$-贪婪策略”采取动作，计算得到10000个样本 $(\vec{s},\vec{a},R(\vec{s}),{\vec{s}}^{\prime })$。(Replay Buffer)
     2. 训练神经网络，迭代设定次数{
       使用“小批量”策略(1000个样本/批)，重复所有批：{
         1. 计算当前批的训练样本，$\vec{x}=(\vec{s},\vec{a})$、$y=R(\vec{s})+\gamma {\max }_{{\vec{a}}^{\prime }}Q({\vec{s}}^{\prime },{\vec{a}}^{\prime })$。
         2. 使用当前批训练神经网络参数，得到新的神经网络 $Q_{new}\approx y$。
       }
     }
     4. “软更新”神经网络参数，比如 $Q=0.1Q_{new}+0.9Q$。
   }

$\epsilon$-贪婪策略
  $\epsilon$-贪婪策略($\epsilon$- greedy policy)可以避免神经网络永远也不会尝试某个动作。因为神经网络初始化的参数不准确，若在拟合 $Q(\vec{s},\vec{a})$ 时总是直接选取$Q$值最大的动作，可能会导致某些动作永远也尝试不到(万一是好动作呢)。所以对动作的选取做出改进：

• 【原始方法❌】在每一个状态选取下一个动作时，总是选取当前神经网络输出最大$Q$值的动作。但由于神经网络一开始的初始化参数不好，可能会导致其永远不会尝试好动作。
• 【$\epsilon$-贪婪策略✅】每次进行选取动作时(假设$\epsilon =0.05$)，以$1-\epsilon$ 的概率选取最大化$Q$值的动作(greedy/exploitation)、以$\epsilon$ 的概率随机选择动作(exploration)。在神经网络初始训练时，可以令 $\epsilon$ 较大，随着训练的进行逐步减小，比如从 $1.0$ 逐步减小到 $0.01$。

注：由于有 $1-\epsilon$ 的概率都是“贪婪的”，貌似“$\epsilon$-贪婪策略”这个名字并不恰当，但这是历史遗留问题。

上述也就是说，$\epsilon$-贪婪策略是“贪婪(exploitation)”和“探索(exploration)”之间的折衷，通过偶尔不选取最佳策略为代价，来学习更多的信息。

小批量
  “小批量(mini-batches)”是一种用于加速神经网络训练的方法，应用该思想也可以加速“线性回归”、“逻辑回归”。假设训练集中有一亿个训练样本，此时计算代价函数时，若直接计算所有样本的均方误差会使得计算量非常庞大。所以对单次迭代过程进行改进：

• 【原始方法❌】计算所有训练样本的均方误差，然后更新一小步。梯度下降方向相对准确，但计算成本非常大。
• 【小批量✅】将一亿个训练样本拆分成1000个为一批(bitch)，然后对每一批，都计算一次均方误差并更新参数。梯度下降的过程相对“混乱”，但也会逐渐趋向代价极小点，并且计算成本大大降低。

软更新

“软更新(soft updates)”可以避免神经网络性能突然变差，进而帮助算法更好的收敛。所以对神经网络参数的更新做出改进：

• 【原始方法❌】直接更新。假设新的神经网络碰巧性能更差，那么直接更新会导致神经网络性能突然变差。
• 【软更新✅】比如设置 $Q=0.1Q_{new}+0.9Q$，可以避免“强化学习”的参数振荡或具有其他不良特性。

  最后总结一下本小节，相比于“有监督学习”，“强化学习”对于参数的选取更加苛刻，这也是为什么“强化学习”还不成熟的原因。比如“有监督学习”中，即使“学习率$\alpha$”的选取较小，可能可只是多花三倍时间进行训练；而在“强化学习”中，若“$\epsilon$”等参数选取不合适，那可能会多花上10倍甚至100倍时间进行训练。

3.5 代码示例-登月器

  “登月器”问题其实已经由OpenAI团队开发好封装在“gymnasium包”中，并且还包括“小车上山”、“双足行走”、“汽车竞速”等一系列强化学习实验。老师给出的原版代码中使用pyvirtualdisplay渲染，这在Windows平台很难用(见下面的bug1)。本节就来使用“gymnasium包+TensorFlow”来加载和训练强化学习场景。

问题要求：使用“gymnasium包+TensorFlow”来加载和训练“登月器”。
代码结构：

• 函数1：计算一批仿真的代价，先计算 $y$，在计算均方误差。
• 函数2：定义代价函数的计算过程(函数1)，并更新网络参数。
• 主函数：见注释。
• utils.py：一些老师写好的杂散的函数。见“课程资料”。

注：本实验来自本周的练习“C3_W3_A1_Assignment.ipynb”，我修改后的原版notebook见“Gymnasium_C3_W3_A1.ipynb(161KB)”。但是下面的代码具有连续性，可以更好的理解整个工程的运行原理。
注：代码中使用了“$\epsilon$-贪婪策略”、“小批量”。但没有使用“软更新”，而是每隔几次仿真更新一次网络。

Jupyter notebook的bug1：
运行pyvirtualdisplay库中的Display()函数时报错FileNotFoundError: [WinError 2] 系统找不到指定的文件。
分析问题
因为pyvirtualdisplay库是专门给Linux用的，所以在Windows用不了。但是gym是OpenAI团队的库，都2023年了早就升级成了gymnasium非常强大，无需调用别的库即可自己实现渲染。所以下面舍弃pyvirtualdisplay、PIL.Image，然后安装gymnasium并修改代码即可。
解决问题：

步骤一：安装gymnasium

1. conda install swig
2. pip install gymnasium[all]
3. 注意后续再报错缺少什么安装什么。

步骤二：更改代码

• 参考我下面的代码即可运行。主要是将pyvirtualdisplay、PIL.Image全部注释掉；再注意env.step(action)、env.reset()函数返回值需要修改。

参考文章:

• gymnasium官网中的“Environments”一节给出了所有可选的强化学习案例环境ID。
• CSDN——“解决安装强化学习库gymnasium，box2d安装报错的问题”。
• CSDN——“gym包更新升级到0.26.2版本后炼丹炉的测试代码”。
• CSDN——“强化学习笔记：Gym入门–从安装到第一个完整的代码示例”。（强化学习笔记总目录）
• CSDN——“强化学习实战——OpenAI Gym环境配置+实战演示（win10）”。

Jupyter notebook的bug2：
最后创建视频时总是报错must be real number, not NoneType
解决问题：

1. 先卸载：pip uninstall moviepy
2. 再重安：pip install moviepy

参考文章：

• gymnasium官网中的“gymnasium.wrappers.RecordVideo()”函数介绍。
• stack overflow——“Getting “TypeError: must be real number, not NoneType” whenever trying to run write_videofile to a clip in moviepy”。

下面是代码和输出结果：
utils.py

import base64
import random
from itertools import zip_longest

import imageio
import IPython
import matplotlib.pyplot as plt
import matplotlib.ticker as mticker
import numpy as np
import pandas as pd
import tensorflow as tf
from statsmodels.iolib.table import SimpleTable


SEED = 0              # seed for pseudo-random number generator
MINIBATCH_SIZE = 64   # mini-batch size
TAU = 1e-3            # soft update parameter
E_DECAY = 0.995       # ε decay rate for ε-greedy policy
E_MIN = 0.01          # minimum ε value for ε-greedy policy


random.seed(SEED)


def get_experiences(memory_buffer):
    experiences = random.sample(memory_buffer, k=MINIBATCH_SIZE)
    states = tf.convert_to_tensor(np.array([e.state for e in experiences if e is not None]),dtype=tf.float32)
    actions = tf.convert_to_tensor(np.array([e.action for e in experiences if e is not None]), dtype=tf.float32)
    rewards = tf.convert_to_tensor(np.array([e.reward for e in experiences if e is not None]), dtype=tf.float32)
    next_states = tf.convert_to_tensor(np.array([e.next_state for e in experiences if e is not None]),dtype=tf.float32)
    done_vals = tf.convert_to_tensor(np.array([e.done for e in experiences if e is not None]).astype(np.uint8),
                                     dtype=tf.float32)
    return (states, actions, rewards, next_states, done_vals)


def check_update_conditions(t, num_steps_upd, memory_buffer):
    """
    判断是否更新网络参数：
        1. 并不是每次仿真完都会更新一次网络参数，而是仿真到达一定次数才更新，比如每4次仿真更新一次。
        2. 后者重放缓冲区满了，要立刻更新参数。
    :param t: 当前仿真次数
    :param num_steps_upd: 每”num_steps_upd“次更新一次。
    :param memory_buffer: 重放缓冲区
    :return:更新网络参数的标志位
    """
    if (t + 1) % num_steps_upd == 0 and len(memory_buffer) > MINIBATCH_SIZE:
        return True
    else:
        return False
    
    
def get_new_eps(epsilon):
    return max(E_MIN, E_DECAY*epsilon)


def get_action(q_values, epsilon=0):
    if random.random() > epsilon:
        return np.argmax(q_values.numpy()[0])
    else:
        return random.choice(np.arange(4))
    
    
def update_target_network(q_network, target_q_network):
    for target_weights, q_net_weights in zip(target_q_network.weights, q_network.weights):
        target_weights.assign(TAU * q_net_weights + (1.0 - TAU) * target_weights)
    

def plot_history(reward_history, rolling_window=20, lower_limit=None,
                 upper_limit=None, plot_rw=True, plot_rm=True):
    
    if lower_limit is None or upper_limit is None:
        rh = reward_history
        xs = [x for x in range(len(reward_history))]
    else:
        rh = reward_history[lower_limit:upper_limit]
        xs = [x for x in range(lower_limit,upper_limit)]
    
    df = pd.DataFrame(rh)
    rollingMean = df.rolling(rolling_window).mean()

    plt.figure(figsize=(10,7), facecolor='white')
    
    if plot_rw:
        plt.plot(xs, rh, linewidth=1, color='cyan')
    if plot_rm:
        plt.plot(xs, rollingMean, linewidth=2, color='magenta')

    text_color = 'black'
        
    ax = plt.gca()
    ax.set_facecolor('black')
    plt.grid()
#     plt.title("Total Point History", color=text_color, fontsize=40)
    plt.xlabel('Episode', color=text_color, fontsize=30)
    plt.ylabel('Total Points', color=text_color, fontsize=30)
    yNumFmt = mticker.StrMethodFormatter('{x:,}')
    ax.yaxis.set_major_formatter(yNumFmt)
    ax.tick_params(axis='x', colors=text_color)
    ax.tick_params(axis='y', colors=text_color)
    plt.show()
    
    
def display_table(initial_state, action, next_state, reward, done):

    action_labels = ["Do nothing", "Fire right engine", "Fire main engine", "Fire left engine"]
    
    # Do not use column headers
    column_headers = None

    with np.printoptions(formatter={'float': '{:.3f}'.format}):
        table_info = [("Initial State:", [f"{initial_state}"]),
                      ("Action:", [f"{action_labels[action]}"]),
                      ("Next State:", [f"{next_state}"]),
                      ("Reward Received:", [f"{reward:.3f}"]),
                      ("Episode Terminated:", [f"{done}"])]

    # Generate table  
    row_labels, data = zip_longest(*table_info)
    table = SimpleTable(data, column_headers, row_labels)

    return table


def embed_mp4(filename):
    """Embeds an mp4 file in the notebook."""
    video = open(filename,'rb').read()
    b64 = base64.b64encode(video)
    tag = '''
    <video width="840" height="480" controls>
    <source src="data:video/mp4;base64,{0}" type="video/mp4">
    Your browser does not support the video tag.
    </video>'''.format(b64.decode())
    return IPython.display.HTML(tag)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133

main.py

import time
from collections import deque, namedtuple
import numpy as np
import logging
import imageio

# 渲染画面的库
# import PIL.Image
# from pyvirtualdisplay import Display

# TensorFlow库
import tensorflow as tf
import keras
from keras.models import Sequential
from keras.layers import Dense, Input
from keras.losses import MSE
from keras.optimizers import Adam

# OpenAI的强化学习环境
# import gym
import gymnasium
import gymnasium as gym

# 额外的文件
import utils


####################################自定义函数####################################
def compute_loss(experiences, gamma, q_network, target_q_network):
    """
    Calculates the loss.
    Args:
      experiences: (tuple) tuple of ["state", "action", "reward", "next_state", "done"] namedtuples
      gamma: (float) The discount factor.
      q_network: (tf.keras.Sequential) Keras model for predicting the q_values
      target_q_network: (tf.keras.Sequential) Karas model for predicting the targets
    Returns:
      loss: (TensorFlow Tensor(shape=(0,), dtype=int32)) the Mean-Squared Error between
            the y targets and the Q(s,a) values.
    """
    # Unpack the mini-batch of experience tuples
    states, actions, rewards, next_states, done_vals = experiences
    # Compute max Q^(s,a)
    max_qsa = tf.reduce_max(target_q_network(next_states), axis=-1)
    # Set y = R if episode terminates, otherwise set y = R + γ max Q^(s,a).
    y_targets = rewards + (1 - done_vals) * gamma * max_qsa
    # Get the q_values
    q_values = q_network(states)
    q_values = tf.gather_nd(q_values, tf.stack([tf.range(q_values.shape[0]),
                                                tf.cast(actions, tf.int32)], axis=1))
    # Compute the loss
    loss = MSE(y_targets, q_values)
    return loss


@tf.function  # 将下面的函数放到TensorFlow中计算
def agent_learn(experiences, gamma):
    """
    Updates the weights of the Q networks.
    Args:
      experiences: (tuple) tuple of ["state", "action", "reward", "next_state", "done"] namedtuples
      gamma: (float) The discount factor.
    """
    # Calculate the loss
    with tf.GradientTape() as tape:
        loss = compute_loss(experiences, gamma, q_network, target_q_network)
    # Get the gradients of the loss with respect to the weights.
    gradients = tape.gradient(loss, q_network.trainable_variables)
    # Update the weights of the q_network.
    optimizer.apply_gradients(zip(gradients, q_network.trainable_variables))
    # update the weights of target q_network
    utils.update_target_network(q_network, target_q_network)


####################################主函数##################################
if __name__ == "__main__":
    # 定义参数
    num_episodes = 2000         # 总仿真次数，这个数字可以非常大
    max_num_timesteps = 1000    # 每次仿真的最大时长(动作总数)
    NUM_STEPS_FOR_UPDATE = 4    # 神经网络参数的更新频率
    GAMMA = 0.995  # 计算回报的折扣因子
    epsilon = 1.0  # ε的初始值(ε-贪婪策略)
    ALPHA = 1e-3   # 学习率-Adam算法
    MEMORY_SIZE = 100_000                      # 重放缓冲区的大小
    memory_buffer = deque(maxlen=MEMORY_SIZE)  # 创建重放缓冲区
    num_p_av = 100            # 查看倒数多少次仿真的回报平均值
    total_point_history = []  # 记录所有仿真的总回报

    # 存储每次执行动作后的信息
    experience = namedtuple("Experience", field_names=["state", "action", "reward", "next_state", "done"])

    # 加载强化学习场景
    env = gym.make('LunarLander-v2', render_mode='human')  # 加载场景
    initial_state, _ = env.reset()                         # 场景初始化
    state_size = env.observation_space.shape  # 状态向量的长度(DQN输入的长度)
    num_actions = env.action_space.n          # 动作的总数：登月器为4
    print(f"当前场景中，状态向量的长度为 {state_size}，可执行的动作数量为{num_actions}。")

    # 运行一个动作
    action = 0  # 先随便选择一个动作
    next_state, reward, done, truncated, info = env.step(action)
    print("\n运行一个动作：")
    with np.printoptions(formatter={'float': '{:.3f}'.format}):
        print("Initial State:", initial_state)
        print("Action:", action)
        print("Next State:", next_state)
        print("Reward Received:", reward)
        print("Episode Terminated:", done)
        print("Info:", info)

    # 定义拟合”Q函数“的神经网络
    tf.random.set_seed(utils.SEED)  # 保证神经网络初始化参数相同
    # q_network用于计算Q值
    q_network = Sequential([
        Input(shape=state_size),
        Dense(64, activation='relu'),
        Dense(64, activation='relu'),
        Dense(num_actions, activation='linear')
    ])
    # target_q_network用于更新迭代
    target_q_network = Sequential([
        Input(shape=state_size),  # 输入特征的长度
        Dense(64, activation='relu'),
        Dense(64, activation='relu'),
        Dense(num_actions, activation='linear')
    ])
    # 两者的初始化参数相同
    target_q_network.set_weights(q_network.get_weights())
    # 优化器
    optimizer = keras.optimizers.Adam(learning_rate=ALPHA)

    # 开始迭代
    start = time.time()
    for i in range(num_episodes):
        # 初始化单次仿真
        state, _ = env.reset()
        total_points = 0  # 本次仿真的总分数

        # 进行单次仿真
        for t in range(max_num_timesteps):
            # 使用ε-贪婪策略，根据当前状态state选择下一动作action
            state_qn = np.expand_dims(state, axis=0)      # 将一维的状态向量state扩展成二维矩阵state_qn
            q_values = q_network(state_qn)                # 计算当前状态state_qn的四个Q值
            action = utils.get_action(q_values, epsilon)  # 使用ε-贪婪策略选择下一动作

            # 计算当前状态的奖励reward，然后执行下一动作action计算下一状态next_state
            next_state, reward, done, _, _ = env.step(action)

            # 使用元组存储四要素(S,A,R,S')到”Replay Buffer“，并且捎带了”终止状态标识done“
            memory_buffer.append(experience(state, action, reward, next_state, done))

            # 每”num_steps_upd“次、或者重放缓冲区满，才更新神经网络参数
            update = utils.check_update_conditions(t, NUM_STEPS_FOR_UPDATE, memory_buffer)
            if update:
                # 从缓冲区取出一个”小批量“的”四要素“数据
                experiences = utils.get_experiences(memory_buffer)
                # 计算目标值y，然后使用Adam算法更新网络参数
                agent_learn(experiences, GAMMA)

            # 更新到下一状态，若到达终止状态则跳出本次仿真
            state = next_state.copy()
            total_points += reward
            if done:
                break

        # 计算最新范围的平均总回报，并判定是否完成仿真：最新范围的平均总回报大于200分
        total_point_history.append(total_points)
        av_latest_points = np.mean(total_point_history[-num_p_av:])
        if av_latest_points >= 200.0:
            print(f"\n\nEnvironment solved in {i + 1} episodes!")
            q_network.save('lunar_lander_model.h5')
            break

        # 减小ε的大小
        epsilon = utils.get_new_eps(epsilon)

        # 打印仿真信息
        if (i + 1) % num_p_av == 0:
            print(f"\rEpisode {i + 1} | Total point average of the last {num_p_av} episodes: {av_latest_points:.2f}")
        else:
            print(f"\rEpisode {i + 1} | Total point average of the last {num_p_av} episodes: {av_latest_points:.2f}",
                  end="")  # 仿真进度

    # 打印仿真总时间
    tot_time = time.time() - start
    print(f"\nTotal Runtime: {tot_time:.2f} s ({(tot_time / 60):.2f} min)")

    # 画出所有仿真的总回报的变化趋势
    utils.plot_history(total_point_history)

    # Suppress warnings from imageio
    # logging.getLogger().setLevel(logging.ERROR)

    # 查看最新的训练效果并保存成视频
    video_folder = './videos'  # 视频存储路径
    env = gym.make("LunarLander-v2", render_mode="rgb_array")
    video_env = gymnasium.wrappers.RecordVideo(env, video_folder)
    done = False
    state, _ = video_env.reset()
    num = 0
    while not done:
        state = np.expand_dims(state, axis=0)
        q_values = q_network(state)
        action = np.argmax(q_values.numpy()[0])
        state, reward, done, _, _ = video_env.step(action)
    # 最后一行代码只是显示视频，只在jupyter notebook起作用
    utils.embed_mp4(video_folder+'/rl-video-episode-0.mp4')  # 视频文件名固定不变
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207

终端输出：

当前场景中，状态向量的长度为 (8,)，可执行的动作数量为4。

运行一个动作：
Initial State: [0.004 1.422 0.368 0.501 -0.004 -0.083 0.000 0.000]
Action: 0
Next State: [0.007 1.433 0.368 0.476 -0.008 -0.082 0.000 0.000]
Reward Received: 0.6011367852468368
Episode Terminated: False
Info: {}

Episode 100 | Total point average of the last 100 episodes: -150.38
Episode 200 | Total point average of the last 100 episodes: -100.94
Episode 300 | Total point average of the last 100 episodes: -44.81
Episode 400 | Total point average of the last 100 episodes: 57.77
Episode 500 | Total point average of the last 100 episodes: 135.13
Episode 598 | Total point average of the last 100 episodes: 198.41

Environment solved in 599 episodes!

Total Runtime: 6827.24 s (113.79 min)

Moviepy - Building video C:\Users\14751\Desktop\LunarLander\videos\rl-video-episode-0.mp4.
Moviepy - Writing video C:\Users\14751\Desktop\LunarLander\videos\rl-video-episode-0.mp4

Moviepy - Done !
Moviepy - video ready C:\Users\14751\Desktop\LunarLander\videos\rl-video-episode-0.mp4
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

如果将训练完成的判断标准改成最后num_p_av个回报的最小值都要满足要求。也就是在main.py168行后新增一行代码计算最后num_p_av个回报的最小值，然后将169行的判断标准变成该最小值，那么结果如下：

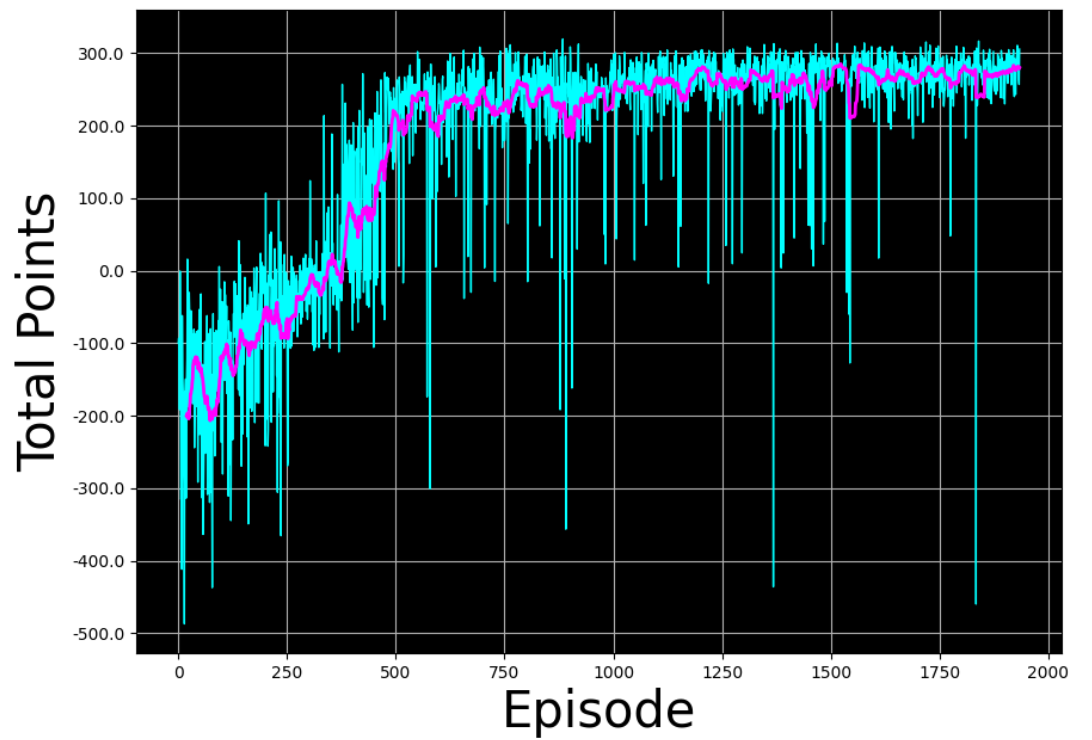
• 上述训练结果的神经网络参数为“lunar_lander_model.h5(34KB)”，需要自取。

本节 Quiz：

1. The Lunar Lander is a continuous state Markov Decision Process (MDP) because:
   √ The state contains numbers such as position and velocity that are continuous valued.
   × The state has multiple numbers rather than only a single number (such as position in the $x$-direction).
   × The reward contains numbers that are continuous valued.
   × The state-action value $Q(s,a)$ function outputs continuous valued numbers.

2. In the learning algorithm described in the videos, we repeatedly create an artificial training set to which we apply supervised learning where the input $x=(s,a)$ and the target, constructed using Bellman’s equations, is y=__?
   × $y=\underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })$ where $s^{\prime }$ is the state you get to after taking action $a$ in states.
   × $y=R(s)$
   √ $y=R(s)+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime })$ where $s^{\prime }$ is the state you get to after taking action $a$ in state $s$.
   × $y=R(s)$ where $s^{\prime }$ is the state you get to after taking action $a$ in state $s$.

3. You have reached the final practice quiz of this class! What does that mean? (Please check all the answers, because all of them are correct!)
   √ The DeepLearning.Al and Stanford Online teams would like to give you a round of applause!
   √ You deserve to celebrate!
   √ What an accomplishment - you made it!
   √ Andrew sends his heartfelt congratulations to you!

4. 课程总结和致谢