L1正则化和L2正则化的区别_l1正则化和l2正则化的区别是

前言

在防止过拟合的方法中有L1正则化和L2正则化，那么这两者有什么区别呢？

一、L1和L2正则化是什么？

L1和L2是正则化项，又叫做惩罚项，是为了限制模型的参数，防止模型过拟合而加在损失函数后面的一项。

二、区别

1. L1是模型各个参数的绝对值之和。
   L2是模型各个参数的平方和的开方值。
2. L1会趋向于产生少量的特征，而其他的特征都是0。
   因为最优的参数值很大概率出现在坐标轴上，这样就会导致某一维的权重为0 ，产生稀疏权重矩阵
   L2会选择更多的特征，这些特征都会接近于0。
   最优的参数值很小概率出现在坐标轴上，因此每一维的参数都不会是0。当最小化||w||时，就会使每一项趋近于0。

三、其他问题

1. 为什么参数越小代表模型越简单？

越是复杂的模型，越是尝试对所有样本进行拟合，包括异常点。这就会造成在较小的区间中产生较大的波动，这个较大的波动也会反映在这个区间的导数比较大。只有越大的参数才可能产生较大的导数。因此参数越小，模型就越简单。

2. 实现参数的稀疏有什么好处？

因为参数的稀疏，在一定程度上实现了特征的选择。一般而言，大部分特征对模型是没有贡献的。这些没有用的特征虽然可以减少训练集上的误差，但是对测试集的样本，反而会产生干扰。稀疏参数的引入，可以将那些无用的特征的权重置为0。

3. L1范数和L2范数为什么可以避免过拟合？

加入正则化项就是在原来目标函数的基础上加入了约束。当目标函数的等高线和L1,L2范数函数第一次相交时，得到最优解。

L1范数：

L1范数符合拉普拉斯分布，是不完全可微的。表现在图像上会有很多角出现。这些角和目标函数的接触机会远大于其他部分。就会造成最优值出现在坐标轴上，因此就会导致某一维的权重为0 ，产生稀疏权重矩阵，进而防止过拟合。

L2范数：

L2范数符合高斯分布，是完全可微的。和L1相比，图像上的棱角被圆滑了很多。一般最优值不会在坐标轴上出现。在最小化正则项时，可以是参数不断趋向于0.最后很小的参数。
假设要求的参数为θ，hθ(x)hθ(x)是我们的假设函数，那么线性回归的代价函数如下：

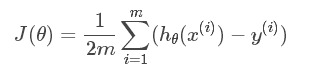
那么在梯度下降法中，最终用于迭代计算参数θj的迭代式为：

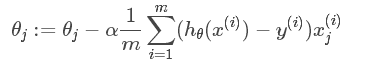
如果在原始代价函数之后添加L2正则化，则迭代公式会变成下面的样子：

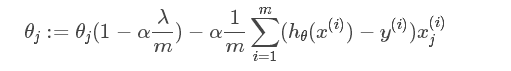
每一次迭代，θj都要先乘以一个小于1的因子，从而使得θj不断减小，因此总得来看，θ是不断减小的。