【优选算法】——Leetcode——202—— 快乐数

 

目录

1.题目 

2. 题⽬分析:

3.简单证明：

4. 解法（快慢指针）：

算法思路：

补充知识：如何求⼀个数n每个位置上的数字的平⽅和。

 总结概括

 5.代码实现

1.C语言

2.C++

---

1.题目 

202. 快乐数

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

• 对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
• 然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
• 如果这个过程 结果为 1，那么这个数就是快乐数。

如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

示例 1：

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

示例 2：

输入：n = 2
输出：false

提示：

• 1 <= n <= 231 - 1

2. 题⽬分析:

为了⽅便叙述，将「对于⼀个正整数，每⼀次将该数替换为它每个位置上的数字的平⽅和」这⼀个操作记为 x 操作；
题⽬告诉我们，当我们不断重复 x 操作的时候，计算⼀定会「死循环」，死的⽅式有两种：
▪ 情况⼀：⼀直在 1 中死循环，即 1 -> 1 -> 1 -> 1...... 
▪ 情况⼆：在历史的数据中死循环，但始终变不到 1 
由于上述两种情况只会出现⼀种，因此，只要我们能确定循环是在「情况⼀」中进⾏，还是在「情
况⼆」中进⾏，就能得到结果。 

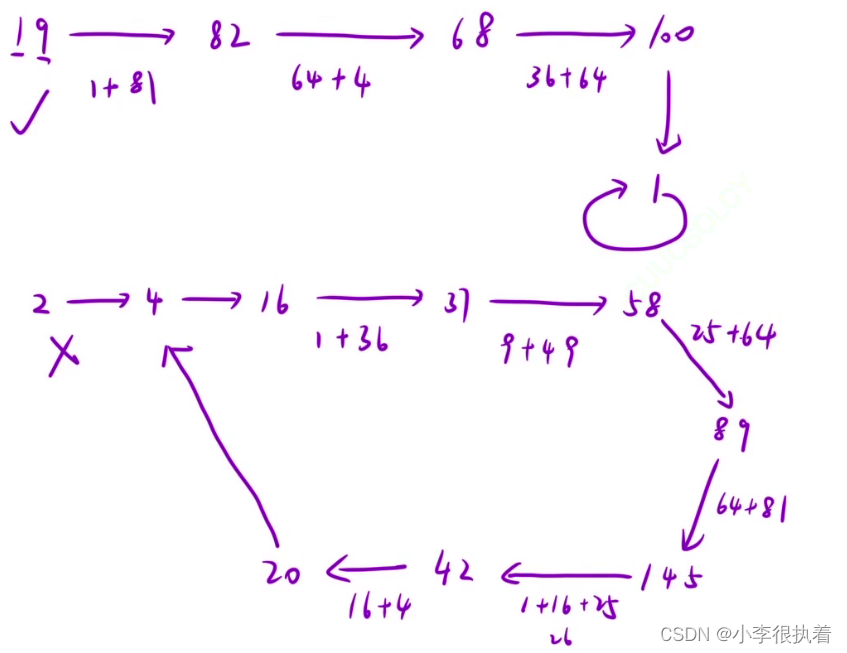
3.简单证明：

a. 经过⼀次变化之后的最⼤值 9^2 * 10 = 810 ( 2^31-1=2147483647 。选⼀个更⼤的最
⼤ 9999999999 )，也就是变化的区间在[1, 810] 之间；
b. 根据「鸽巢原理」，⼀个数变化 811 次之后，必然会形成⼀个循环；
c. 因此，变化的过程最终会⾛到⼀个圈⾥⾯，因此可以⽤「快慢指针」来解决。

4. 解法（快慢指针）：

算法思路：

根据上述的题⽬分析，我们可以知道，当重复执⾏ x 的时候，数据会陷⼊到⼀个「循环」之中。⽽「快慢指针」有⼀个特性，就是在⼀个圆圈中，快指针总是会追上慢指针的，也就是说他们总会相遇在⼀个位置上。如果相遇位置的值是 1 ，那么这个数⼀定是快乐数；如果相遇位置不是 1 的话，那么就不是快乐数。 

补充知识：如何求⼀个数n每个位置上的数字的平⽅和。

a. 把数n 每⼀位的数提取出来：
循环迭代下⾯步骤：
i. int t = n % 10 ?提取个位；
ii. n /= 10 ⼲掉个位；
直到 n 的值变为 0 ；
b. 提取每⼀位的时候，⽤⼀个变量 tmp 记录这⼀位的平⽅与之前提取位数的平⽅和
▪ tmp = tmp + t * t

 总结概括

1.定义快慢指针
2.慢指针每次向后移动一步快指针每次向后移动两步
3.判断相遇时候的值即可

 5.代码实现

1.C语言

 int bitSum(int n)
    {// 返回 n 这个数每⼀位上的平⽅和{
    int sum = 0;
    while (n)
    {
        int t = n % 10;
        sum += t * t;
        n /= 10;
    }
    return sum;
} 
bool isHappy(int n) {
    int slow = n, fast = bitSum(n);
    while (slow != fast) {
        slow = bitSum(slow);
        fast = bitSum(bitSum(fast));
    }
    return slow == 1;
}

2.C++

class Solution 
{
public:
    int bitSum(int n)
    {// 返回 n 这个数每⼀位上的平⽅和{
    int sum = 0;
    while (n)
    {
        int t = n % 10;
        sum += t * t;
        n /= 10;
    }
    return sum;
} 
bool isHappy(int n) {
    int slow = n, fast = bitSum(n);
    while (slow != fast) {
        slow = bitSum(slow);
        fast = bitSum(bitSum(fast));
    }
    return slow == 1;
}
}
;