2024.5.29晚训参考代码

因为本套题没有BFS例题，所以我先把BFS模板放着

#include<bits/stdc++.h>
using namespace std;
int n,m;//n*m的棋盘 
int dis[402][402]; 
bool vis[402][402];
int X[]={-2,-2,-1,-1,1,1,2,2};//偏移量的表 
int Y[]={-1,1,-2,2,-2,2,-1,1};//定义一个数组，我直接把这些元素从0位置填充进去 
struct node{
	int x;
	int y;
	int dis;//从起点走到当前(x,y)的最短步数 
};
int st,ed;//起点x  y坐标 
void bfs(){  
	queue<node>q;
	node now;
	now.x=st;
	now.y=ed;
	now.dis=0;
	q.push(now);//放入队列，第一个搜索的状态 dfs(st,ed,0)  
	while(!q.empty()){
		//第一步取出队首状态
		//第二步，弹出队首 
		//第三步  判断当前状态是不是已经走过了   后面再来到这个点肯定不是最短距离
		//仅限于所有距离都一样的情况   
		//第四步   判断当前的点是不是终点 
		//第五步  打标记
		//第六步  做相关的数据统计  比如记录(now.x,now.y)的最小步数  
		//第七步  以这个点拓展出去的其余状态  注意判断非法情况   
	}
	//bfs结束 
}
signed main(){
	int x,y;
	cin>>n>>m;
	cin>>st>>ed;
	//memset(dis,-1,sizeof(dis));//初始化数组    
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			dis[i][j]=1e9;//表示不可到达  
		}
	}//dis[i][j]表示从起点走到(i,j)的最短距离 
	bfs();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
		//	dis[i][j]=1e9;//表示不可到达  
			if(dis[i][j]==1000000000)cout<<-1;
			else cout<<dis[i][j];
			cout<<" ";
		}
		cout<<'\n';
	}
	return 0;
}

马的便利  
#include<bits/stdc++.h>
using namespace std;
struct node{
	int x;
	int y;
	int dis;//从起点走到(x,y)的距离 
}; 
int n,m,x,y;
int X[]={-1,-1,-2,-2,1,1,2,2};
int Y[]={2,-2,-1,1,2,-2,1,-1};
int dis[405][405];
int vis[405][405];
void bfs(){
	queue<node>q;
	node now;
	now.x=x;
	now.y=y;
	now.dis=0;
	q.push(now);
	while(!q.empty()){
		node now=q.front();
		q.pop();
		if(vis[now.x][now.y]==1){
			continue;//已经走过这个点了  
		}
		dis[now.x][now.y]=now.dis;
		vis[now.x][now.y]=1;
		node cnt;
		for(int i=0;i<8;i++){
			cnt.x=now.x+X[i];
			cnt.y=now.y+Y[i];
			cnt.dis=now.dis+1;
			if(cnt.x<1||cnt.x>n||cnt.y<1||cnt.y>m)continue;
			q.push(cnt);
		}
	}
}
int main(){
	cin>>n>>m>>x>>y;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			dis[i][j]=-1;
		}
	}
	bfs();
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			cout<<dis[i][j]<<"  ";
		}
		cout<<'\n';
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109

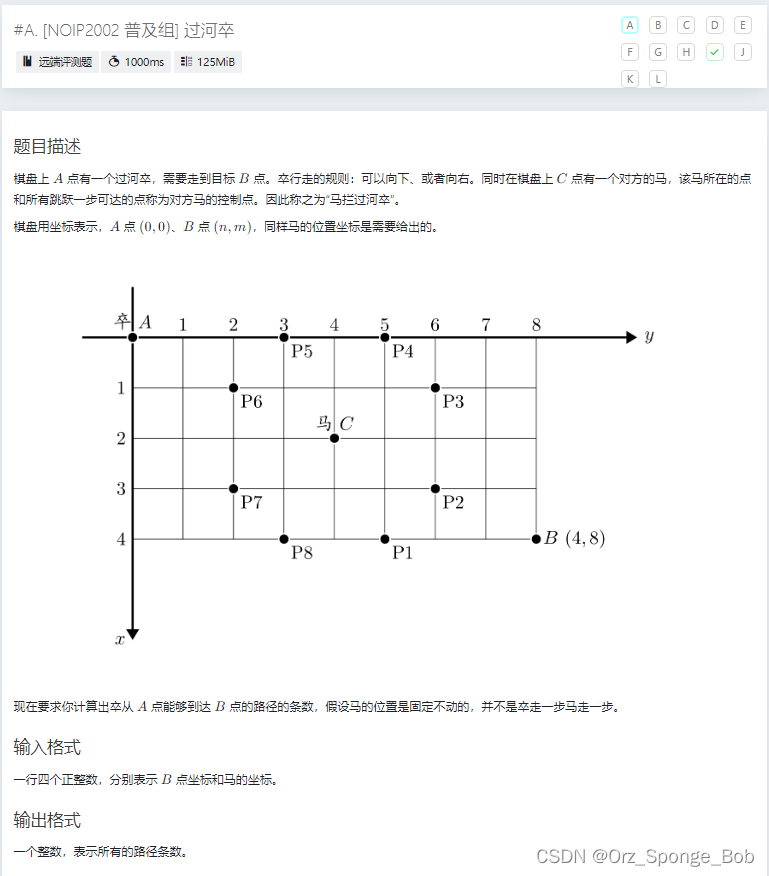
需要考虑记忆化处理

#include<bits/stdc++.h>
using namespace std;
#define int long long 
int vis[30][30];
int n,m,s,b;
int dfs(int x,int y){
	if(x<0||y<0)return 0;
	if((x==s&&y==b)||(x==s-1&&y==b-2)||(x==s-2&&y==b-1)||(x==s-2&&y==b+1))return 0;
	if((x==s-1&&y==b+2)||(x==s+1&&y==b+2)||(x==s+2&&y==b+1)||(x==s+2&&y==b-1)||(x==s+1&&y==b-2))return 0;
	if(x==0&&y==0)return 1;
	if(vis[x][y])return vis[x][y];
	return vis[x][y]=dfs(x-1,y)+dfs(x,y-1);	
}
signed main() {
	cin>>n>>m>>s>>b;
	cout<<dfs(n,m);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

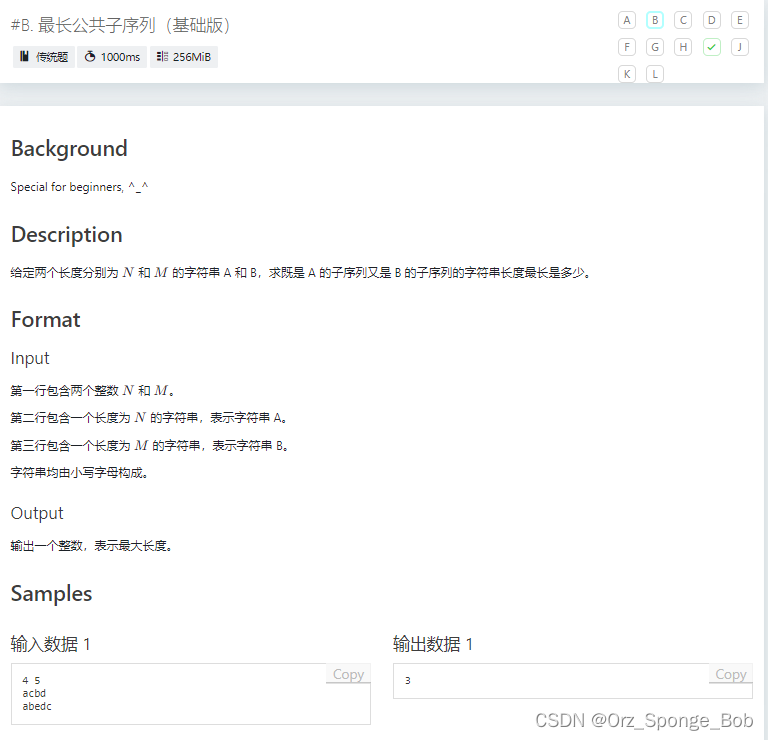
#include<bits/stdc++.h>
using namespace std;
char A[1005];
char B[1005];
int dp[1005][1005];
int main(){
	int n,m;
	cin>>n>>m;
	cin>>A+1>>B+1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<=m;j++){
			if(A[i]==B[j]){
				dp[i][j]=dp[i-1][j-1]+1;
			}
			else{
				dp[i][j]=max(dp[i-1][j-1],max(dp[i-1][j],dp[i][j-1]));
			}
		}
	}
	cout<<dp[n][m];
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

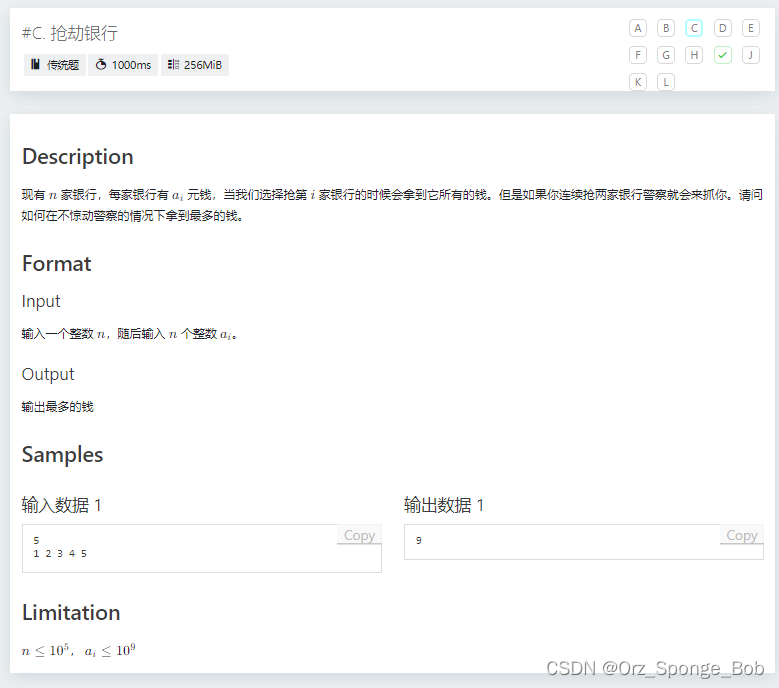
#include<bits/stdc++.h>
using namespace std;
long long dp[100005][2];
int main() {
	int n;
	cin>>n;
	//dp[0][0]=dp[0][]
	//dp[i][0] 没抢i银行  
	for(int i=1;i<=n;i++){
		long long x;
		cin>>x;
//		cout<<i<< "  ";
		dp[i][0]=max(dp[i-1][0],dp[i-1][1]);//没抢 
		dp[i][1]=dp[i-1][0]+x; 
//		cout<<dp[i][0]<<" "<<dp[i][1]<<'\n';
	}
	cout<<max(dp[n][0],dp[n][1]);
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

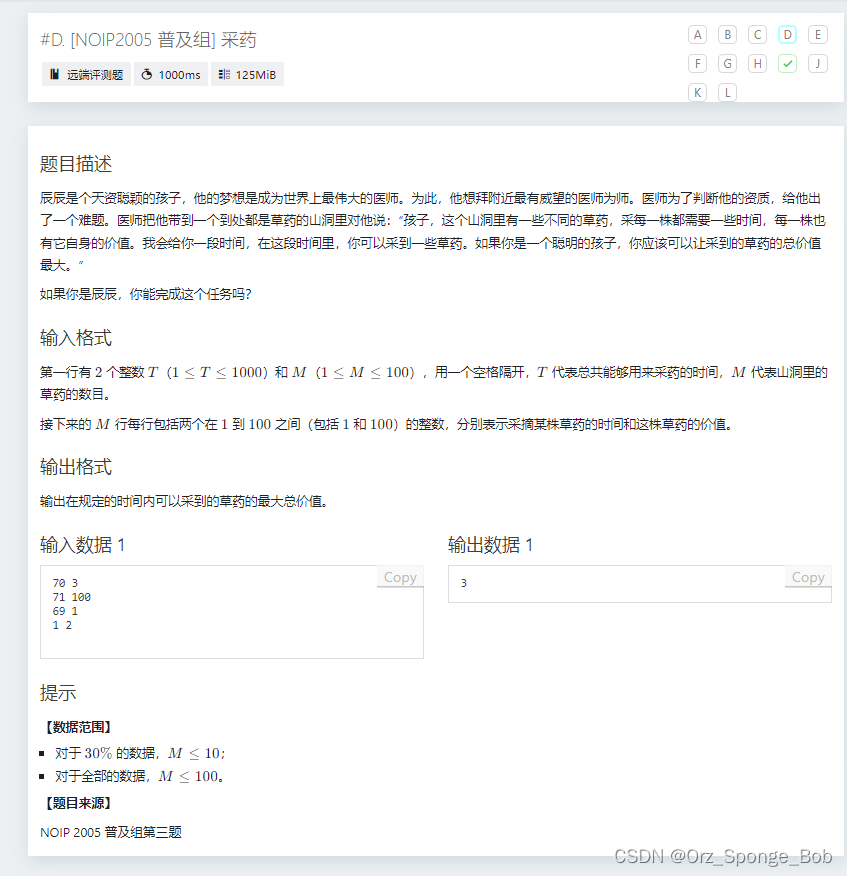
物品只拿一次，01背包

#include<bits/stdc++.h>
using namespace std;
int V[1005],W[1005];// 
int dp[1005];
//有一大堆财宝，体积分别是V[i]  价值是W[i]  
//你现在有一个体积为M的包，你想知道怎么样拿 能保证  在背包容量的限制下 拿到最多价值的财宝   
signed main(){
    //总背包容量10   
	//只考虑拿价值高的    价值是10，体积是10     可能有其他财宝价值5  体积1  有若干个    
	//dfs(拿/不拿)  暴力   n<=20  
	/*背包dp   01背包   
	dp[i][j]  表示处理完前i个物品 有j的容量  
	单独考虑处理第i个物品，那么是不是跟dp[i-1][] + 如何处理第i个物品=> dp[i][]  有关联 
	如果第i个物品你要拿 
	因为你拿了第i个物品，体积变大，变成了dp[i][j]  
	dp[i][j] = dp[i-1][j-V[i]] + W[i] 
	如果我们不拿第i个物品  变到了dp[i][j]  
	dp[i][j] =dp[i-1][j]  
	?????我们的容量j  
	
	dp[i][j] =max(dp[i-1][j],dp[i-1][j-V[i]]+W[i]);  
	    // j=?+V[i] 
	 */
	 int M,n;
	 cin>>M>>n;//M是总体积  n是物品个数   
	 for(int i=1;i<=n;i++){
	 	cin>>V[i]>>W[i];//输入体积  和  价值  
	 }
	for(int i=1;i<=n;i++){
		for(int j=M;j>=V[i];j--){
			dp[j]=max(dp[j],dp[j-V[i]]+W[i]);
		}
	}
	cout<<dp[M];
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

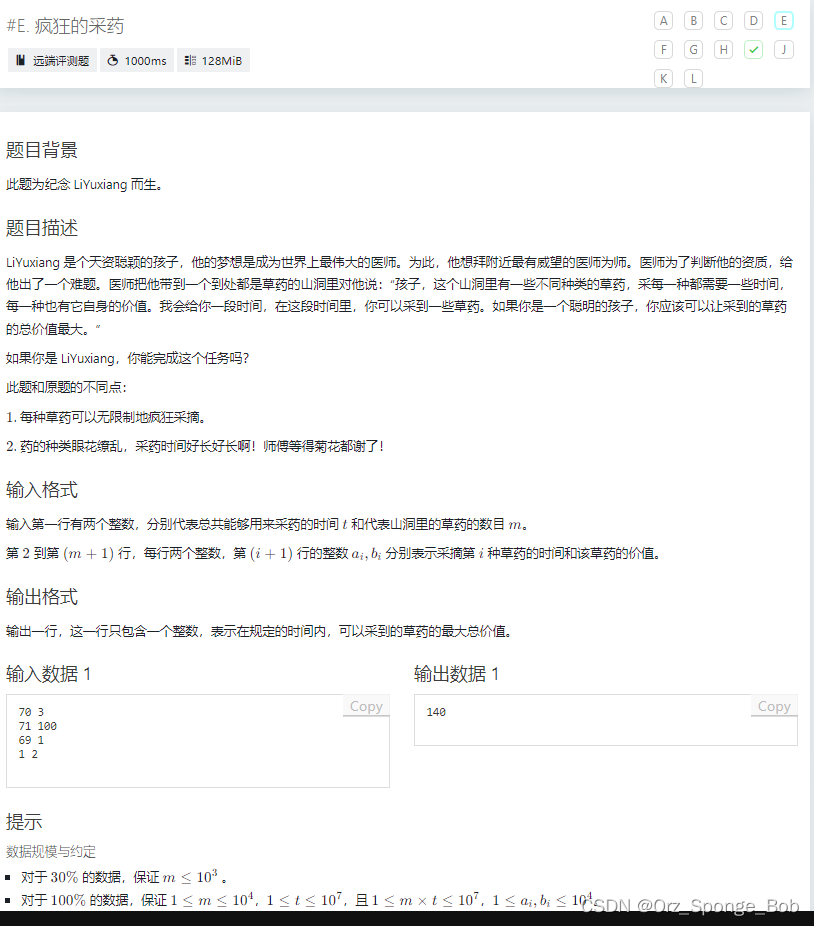
#include<bits/stdc++.h>
using namespace std;
long long T,M,t[10001],v[10001],dp[10000001];
int main(){
	cin>>T>>M;
	for(int i=1;i<=M;i++)
		cin>>t[i]>>v[i];
	for(int i=1;i<=M;i++)
		for(int j=t[i];j<=T;j++)
			dp[j]=max(dp[j],dp[j-t[i]]+v[i]);
    cout<<dp[T];
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13

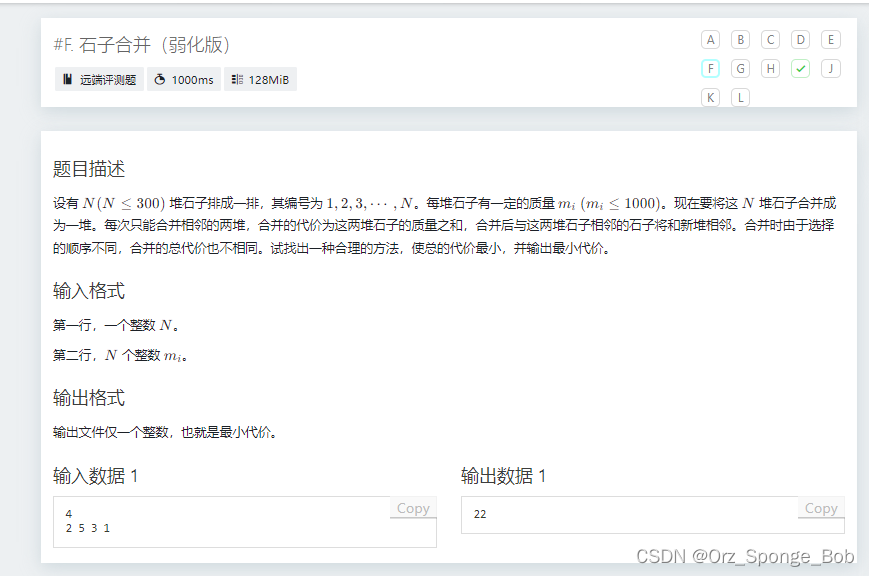
#include<bits/stdc++.h>
using namespace std;
int dp[305][305];
int w[305];
int sum[305];
signed main(){
    /* 考虑区间dp 
	 dp[l][r]= 表示把[L,R]的石头合并成一堆所需要的最小花费   
	 
	 考虑转移
	 1 1 1 1 1 1 1
	 所有大的区间一定由小区间转移 
	 考虑合并成长度为2的区间
	// dp[i][i+1]=(dp[i][i]+dp[i+1][i+1])+w[i]+w[i+1] 
	 合并成3区间  来自于长度为2 + 拼长度为1  
	 长度为4的区间  1+3  2+2  3+1  .... 
	 考虑dp[l][r] 拆成两个区间，进行合并  */
	 int n;
	 cin>>n;
	 for(int i=1;i<=n;i++){
	 	cin>>w[i];
	 	sum[i]=sum[i-1]+w[i];//前缀和 
	 }

	  for(int len=1;len<=n;len++){	 
		
		for(int i=1;i<=n;i++){
	 	    //i作为区间起点
		 	//枚举区间长度
			//计算右端点在哪
			int j=i+len;
			dp[i][j]=1e9;
			if(j>n)break; 
		 	for(int k=i;k<j;k++){
		 		dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]+sum[j]-sum[i-1]);
			 }
		 }	
	 } 
	  cout<<dp[1][n];
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

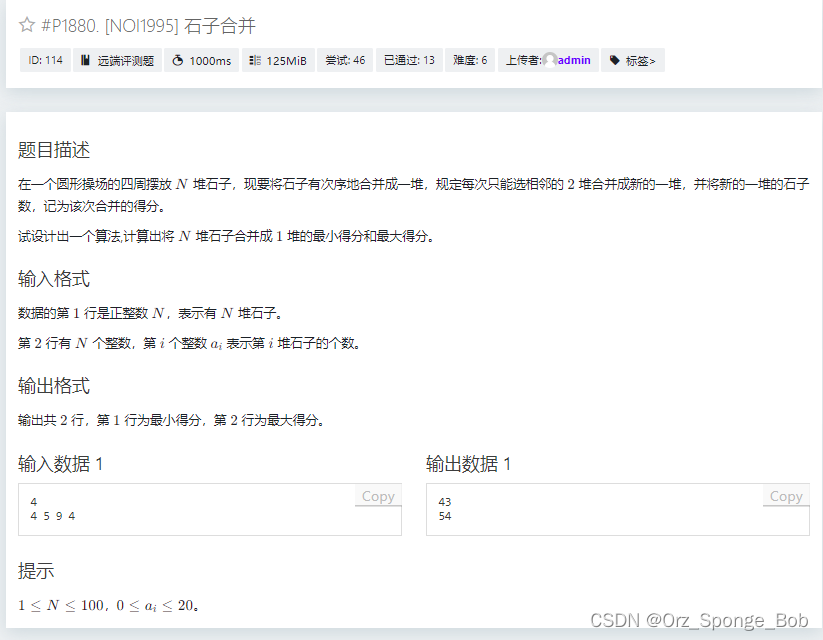
#include<bits/stdc++.h>
using namespace std;
int n;
int minx = 0x3f3f3f3f,maxn = -1;
int s[305];
int m[305];
int dp1[305][305];
int dp2[305][305];
int main()
{
	cin >> n;
	for(int i = 1; i <= n; i++){
		cin >> m[i];
		m[i + n] = m[i];
	}
	memset(dp1,0x3f3f3f3f,sizeof(dp1));
	memset(dp2,-1,sizeof(dp2));
	for(int i = 1; i <= n * 2; i++){
		s[i] = s[i - 1] + m[i];
		dp1[i][i] = 0;
		dp2[i][i] = 0;
	}
	for(int i = 2; i <= n; i++){
		for(int l = 1; l <= n * 2 - i + 1; l++){
			int r = l + i - 1;
			for(int j = l; j < r; j++){
				dp1[l][r] = min(dp1[l][r],dp1[l][j] + dp1[j + 1][r]);
				dp2[l][r] = max(dp2[l][r],dp2[l][j] + dp2[j + 1][r]);
			}
			dp1[l][r] += (s[r] - s[l - 1]);
			dp2[l][r] += (s[r] - s[l - 1]);
		}
	}
	for(int i = 1; i <= n; i++){
		minx = min(minx,dp1[i][i + n - 1]);
		maxn = max(maxn,dp2[i][i + n - 1]);
	}
	cout << minx << "\n" << maxn;
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

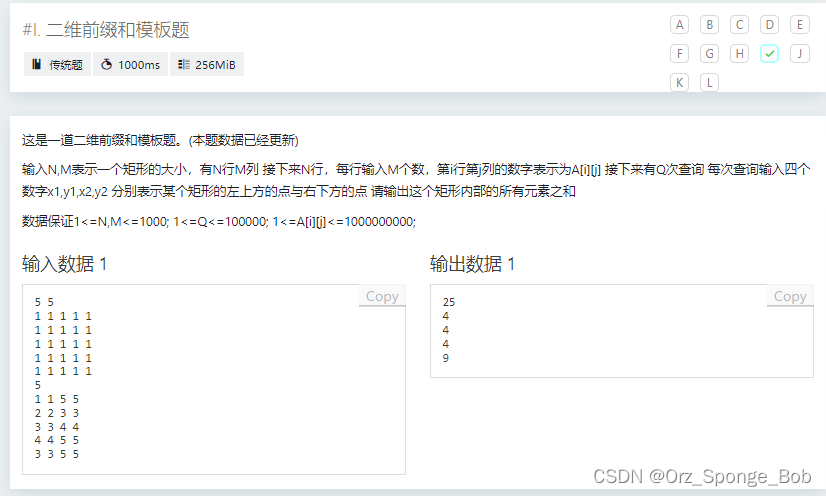
注意输出格式啊。。。。注意数据类型 long long

#include <bits/stdc++.h>
using namespace std;
int n, m;
int a[1005][1005];
long long sum[1005][1005];
int main() {
	cin >> n >> m;
	for(int i = 1; i <= n; i++) {
		for(int j = 1; j <= m; j++) {
			cin >> a[i][j];
		}
	}
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= m; j++) {
			sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + a[i][j];
		}
	}
	int q; cin >> q;
	while(q--) {
		int X1, Y1, X2, Y2;
		cin >> X1 >> Y1 >> X2 >> Y2;
		cout << sum[X2][Y2] - sum[X1 - 1][Y2] - sum[X2][Y1 - 1] + sum[X1 - 1][Y1 - 1] << '\n';
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

#include<bits/stdc++.h>
using namespace std;
int a[100005];
long long int pre[100005];
long long int sum[100005];
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=1; i<=n; i++)
    {
        scanf("%d",&a[i]);
        pre[i]=a[i]-a[i-1];
    }

//1   2   3   4   5
//+2      -2
//+3          -3
    int m;
    scanf("%d",&m);
    while(m--)
    {
        int l,r,x;
        scanf("%d%d%d",&l,&r,&x);
        pre[l]+=x;
        pre[r+1]-=x;
    }
    int st,ed;
    scanf("%d%d",&st,&ed);
    long long int ans=0;
    long long int cnt=0;
    for(int i=1;i<=n;i++){
        sum[i]=sum[i-1]+pre[i];
    }

    for(int i=st; i<=ed; i++)
    {
        ans+=sum[i];

    }

    printf("%lld",ans);

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44

#include<bits/stdc++.h>
#define debug(...) fprintf(stderr,__VA_ARGS__)
#define all(x) x.begin(),x.end()
using namespace std;
const double eps=1e-8;
const double PI=acos(-1.0);
typedef long long ll;
template<class T>int chkmin(T &a,T b){return a>b?a=b,1:0;}
template<class T>int chkmax(T &a,T b){return a<b?a=b,1:0;}
template<class T>T sqr(T a){return a*a;}
template<class T>T mmin(T a,T b){return a<b?a:b;}
template<class T>T mmax(T a,T b){return a>b?a:b;}
template<class T>T aabs(T a){return a<0?-a:a;}
#define min mmin
#define max mmax
#define abs aabs
int a[1024][1024];
int main(){
#ifdef cnyali_lk
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
#endif
    int n,m,xa,ya,xb,yb;
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;++i){
        scanf("%d%d%d%d",&xa,&ya,&xb,&yb);
        ++a[xa][ya];
        --a[xb+1][ya];
        --a[xa][yb+1];
        ++a[xb+1][yb+1];
    }
    for(int i=1;i<=n;++i)for(int j=1;j<=n;++j)printf("%d%c",a[i][j]+=a[i-1][j]+a[i][j-1]-a[i-1][j-1],j==n?'\n':' ');
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

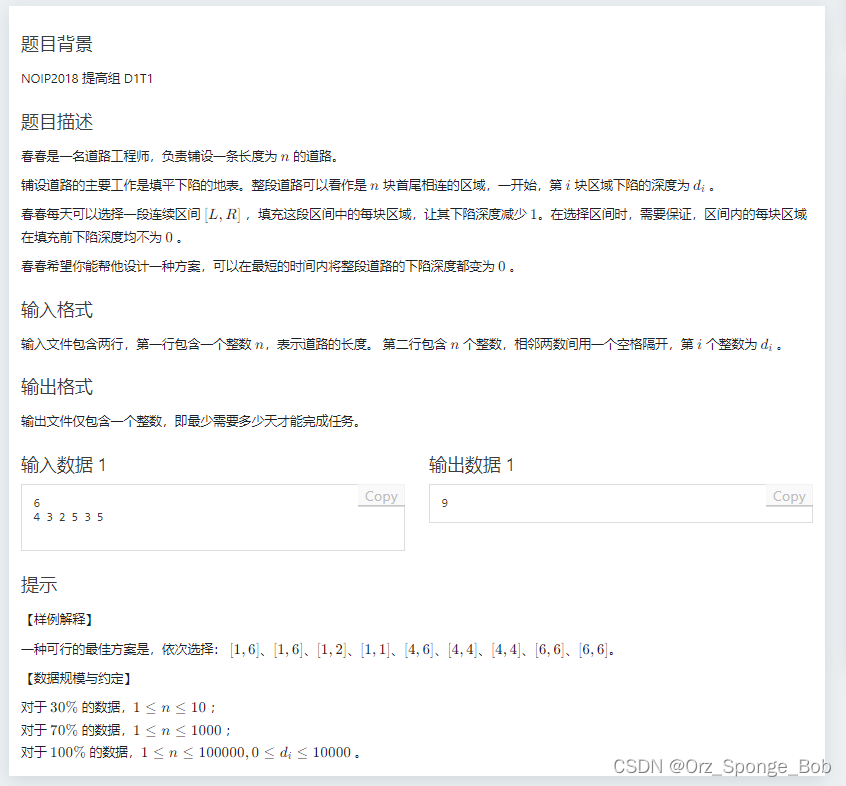
答案   A【1】+ 枚举i=2~n 里面所有的A[i]>A[i-1] 的情况的差  
1