图神经网络元学习

来源：RUC AI Box
 
本文约5000字，建议阅读10分钟本文主要介绍了元学习在GNN中的应用。

图神经网络（GNN）在实际应用中往往会受到可用样本数量太少的限制，而元学习（meta-learning）作为解决机器学习中样本缺乏问题的重要框架，正逐渐被应用到 GNN 领域以解决该问题。本文梳理近年来在元学习应用于 GNN 的一系列研究进展，我们根据模型的架构、共享的表示和应用的领域对以往工作进行分类，并在最后讨论该领域当前有待解决的问题和未来值得关注的研究方向。

1、引言

图结构数据（Graph）广泛存在于现实场景中，例如药物研究中的药物分子结构和推荐系统中的用户商品交互都可以用图（Graph）表示，而图数据（Graph）的广泛存在也促进了图神经网络（GNN）的发展。GNN 是专门用于处理图数据的深度神经网络，它将图或图上的顶点、边映射到一个低维空间，从而学习得到图的有效表示，并进一步将其应用于下游任务。近年来，GNN 被广泛应用于新药发现、交通预测、推荐系统等各个领域。

尽管 GNN 拥有非常强大的能力，但在实际应用中依然面临样本数量有限的挑战，特别是在推荐系统等真实系统更是要求 GNN 可以在少量样本可用的情况下适应新问题。而元学习（meta-learning）作为解决深度学习系统中样本缺乏问题的重要框架，在自然语言处理、机器人技术等多种应用中都取得了成功。因此，如何利用元学习解决 GNN 所面临的样本缺乏问题，是研究人员普遍关心的问题。

元学习的主要思想是利用之前的学习经验来快速适应一个新问题，从而利用很少的样本就能学习一个有用的算法。具体来讲，元学习旨在以先验的形式学习一个模型，而不是针对所有任务学习一个模型(不能区分任务)或针对每个任务学习单独的模型(可能对每个任务过拟合)。元学习应用于 Graph 的主要挑战是如何确定跨任务共享的表示类型，以及怎样设计有效的训练策略。近期，研究人员针对不同的应用场景，已经提出了多种元学习方法来训练 GNN。本文我们就将对元学习在 GNN 上的运用进行全面回顾。

2 背景知识

图神经网络（GNN）

我们首先简要描述 GNN 的主要架构。图卷积网络(GCN)是最具代表性的图神经网络，GCN 将卷积神经网络(CNN)应用到 Graph 上，类似于 CNN 滤波器用邻近像素的信息表示中心像素，GCN 也应用了从节点的局部邻域聚集特征信息的关键思想。具体来讲，GCN 通过将邻接矩阵 A 、节点特征 X 作为输入，为每个节点生成 d 维嵌入表示，即一个 2 层的 GCN 网络可以被定义为：

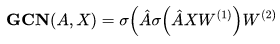
其中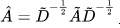为标准化邻接矩阵 (normalized adjacency matrix)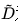为加权度矩阵(degree matrix)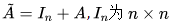， 的单位矩阵 为激活函数是训练过程中要学习的第 i 层的权值矩阵。此外，不同于 GCN，Hamilton 等人还提出了可以泛化到不可见的节点的归纳式 GNN 框架 GraphSAGE。GraphSAGE 在节点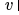 上迭代时，它使用聚集函数 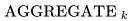聚集节点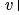 的邻居表示，并将聚集得到的邻域表示 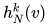与节点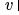的当前表示拼接，然后通过一个全连接层。具体而言，第 k 次迭代可以表示为：

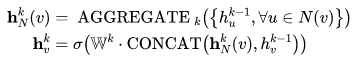
基于上述框架，GNN 领域已发展出图注意网络(GAT) 、图自编码器（Graph Autoencoder）、循环图神经网络（Recurrent GNN）等不同变种，这些变种分别应用于节点分类、链接预测和图分类三个主要任务上。

元学习（Meta-Learning）

元学习是机器学习应用中解决训练数据有限问题的重要策略，其主要思想是利用之前的学习经验，设计仅利用很少的样本就可以快速适应新问题的算法。为形式化表示元学习，我们首先回顾在标准的有监督学习框架之下，给定训练数据集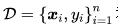 和损失函数 l ，此时目标是找到一个形为 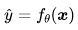的预测函数，即：

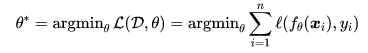
而在元学习中，我们从许多不同的任务中获得训练样本，目标是学习一种能够泛化多个任务的算法。具体来讲，任务可能是从分布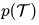 中提取的，而元目标是找到可以作用于多个任务的公共参数，即元知识 (meta-knowledge) ：

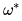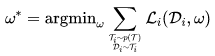
在测试阶段，我们使用元知识在给定的任务 task 0 上测试得到最佳参数，即：

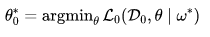
在训练阶段，主流的元学习算法大多基于梯度下降对元参数（meta-parameter）进行优化，这里我们可以抽象出双层优化问题（bi-level optimization problem）：

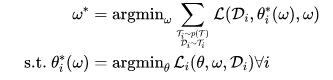
虽然元学习取得了巨大的成功，但我们还没有完全理解元学习的理论基础。当前比较流行的元学习的解释是，我们认为不同的任务共享一个公共的共享表示和一个特定于任务的表示，如果从元学习的训练过程中学习到共享表征，那么之后只需少量样本就可以学习到新任务的特定任务表征，从而得到最终表征。

3 概览

当前已有诸多 GNN 元学习的工作被提出，根据他们的下游任务（Node classification、Link Prediction Graph、Classification）和所共享的的表征类型（Node/Edge Level、Graph Level），我们将现有工作汇总如下：

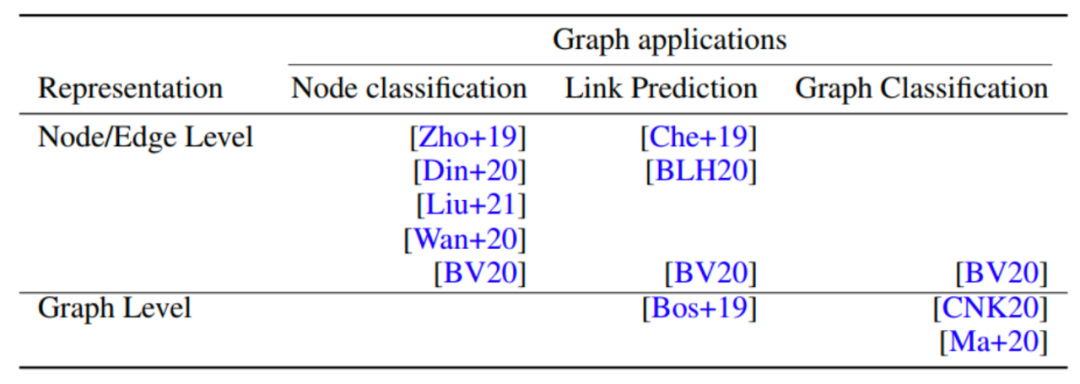
接下来，我们将从下游的图任务和共享的的表征类型两个角度，介绍现有的 GNN 元学习工作。

4 元学习在图任务上的应用

我们首先回顾元学习在解决经典图问题中的应用。这一部分，我们假设底层的图结构是固定不变的，图上节点和边的特征也不随任务的改变而改变。

节点嵌入（Node Embedding）

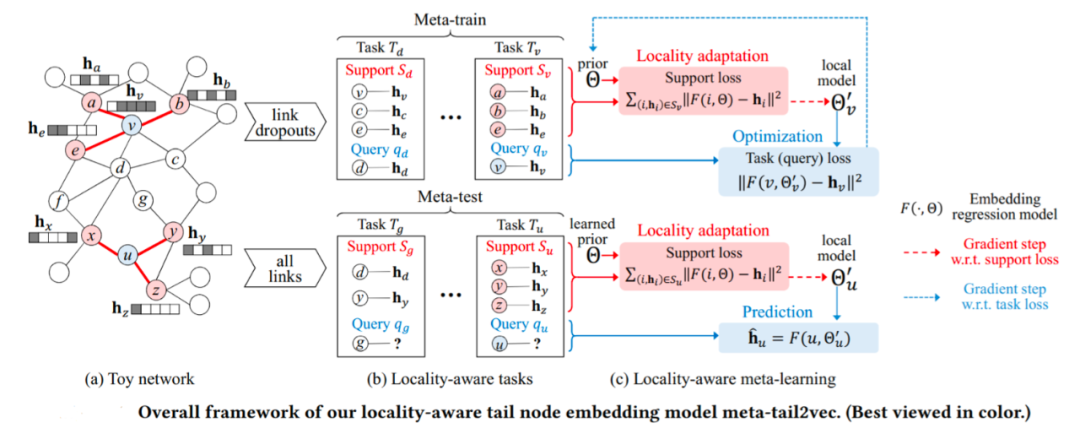
节点嵌入的目标是学习图中节点的表示，以便任何下游应用程序可以直接使用这些表示，而无需考虑原始图。由于大多数图的度分布遵循幂律分布，且节点多而连接少，长尾问题严重，这给节点嵌入的学习带来了挑战。发表于 CIKM  2020 的 meta-tail2vec 借助 MAML 元学习来解决该挑战。meta-tail2vec 建立了一个回归问题来学习节点嵌入，以此捕捉节点嵌入学习过程中的共同先验。由于 high-degree 节点的结构信息丰富，其表示被认为是准确的，所以它们被用作元训练集（meta training）来学习共同先验。low-degree 节点只有少量的邻居，结构信息匮乏，所以用于学习其表示的回归问题被作为元测试（meta-testing）问题，而借助由 high-degree 节点学习得到的共同先验，我们使用少量的样本即可学习这些 low-degree 节点的嵌入。

节点分类（Node Classification）

节点分类任务的目的是推断给定的部分标记图中节点的缺失标签，这个问题在文档分类和蛋白质分类等不同的场景中均有出现。然而，现实中许多类别通常是新颖的，它们只有很少的标记节点。这恰恰给 meta-learning 和 few-shot learning 带来用武之地。发表于 CIKM 2019 的 Meta-GNN 将元学习框架应用于图的节点分类问题，它使用拥有许多标记样本的类来学习可转移表示，在元测试阶段，这种共享表征被用来对具有少量标记样本的新类别进行预测。而发表于 AAAI 2021 的 RALE 认为学习任务中节点之间的依赖关系也很重要，并提出使用中心性得分高的节点(hub nodes)来更新 GNN 学习到的表示。RALE 是通过选择一小组 hub 节点来完成的，对于每个节点 v，考虑从这组 hub 节点到节点 v 的所有路径。

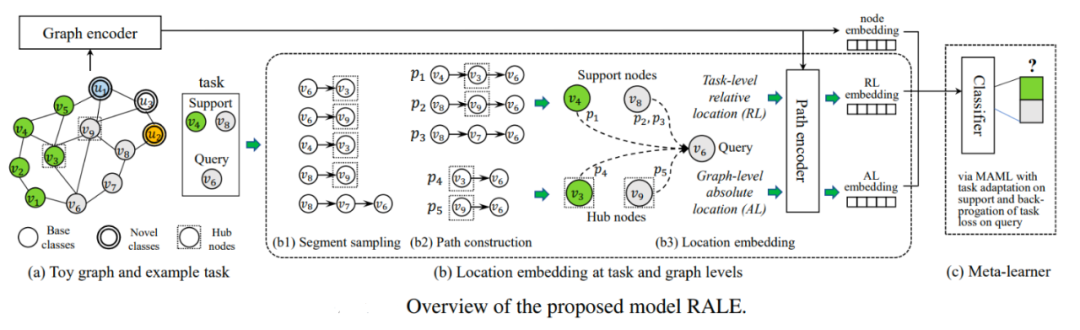
链接预测（Link Prediction）

元学习也可用于通过多关系图（multi-relational graph）中的边/链学习新的关系。多关系图在知识图谱、药物相互作用预测等很多领域均有应用，其中的边由两个端点和一个关系组成的三元组表示。多关系图中链路预测的目标是在给定关系r的一个端点的情况下，通过观察几个关于 r 的三元组来预测新的三元组。这个问题具有挑战性因为通常只有少数关联三元组可用。发表于 EMNLP 2019 的 MetaR 利用元学习通过两步解决链接预测问题，即 (1)Relation-Meta Learner 从 support set 的头尾嵌入生成元关系（relation meta），(2)Embedding Learner 通过端点嵌入和元关系计算 support set 中三元组的真实值。

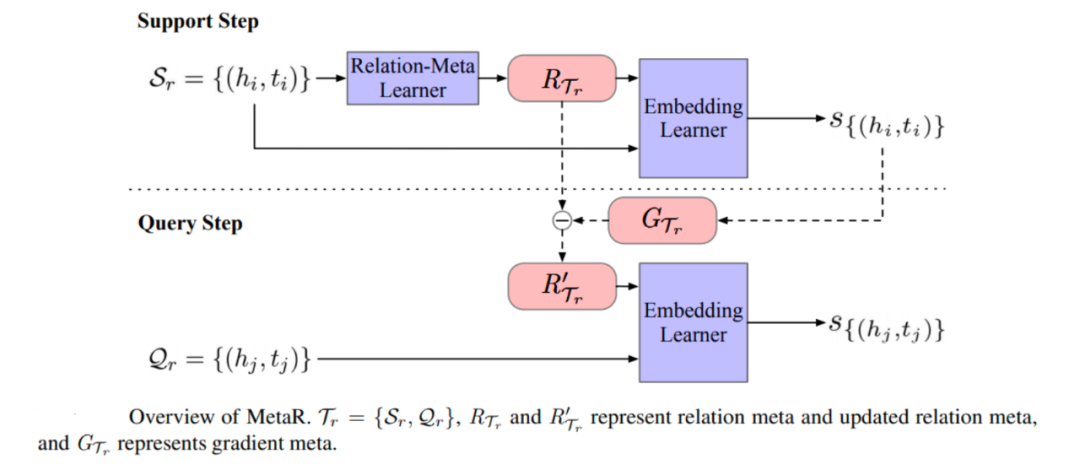
此外，多关系图中有新节点加入时的链接预测问题也受到了人们的关注， NIPS 2020 的 GEN（Graph Extrapolation Network）预测可见节点和不可见节点之间以及不可见节点之间的联系。其主要思想是将给定图中的实体随机分割为模拟不可见实体的元训练集（meta-training set）和真实不可见实体的元测试集（meta-test set）。

5 Meta-Learning on GNN

除上述场景外，还有很多 GNN 元学习设定 Graph 在不同任务中是变化的，即节点、边特征发生变化或网络结构随任务发生变化。这些工作大多基于共享表征，并且根据共享表征的层次可以将他们分为局部级（节点/边）和全局级（图）。此外，大多数现有的工作采用 MAML 算法来训练 GNNs，其中 MAML 的外部循环更新了共享参数，而内部循环更新了当前任务的任务特定参数。

节点/边共享表征（Node/Edge Level Shared Representation）

我们首先考虑局部的共享表征，即基于节点/边的设置。发表于 NIPS 2020 的 G-META 考虑了节点分类问题，其中输入图和标签可以在不同任务中不同。他们分两步学习每个节点 u 的表示，（1）根据到节点 u 的最短路径距离，抽取得到子图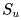 ，（2）将子图 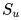通过一个 GCN 学习得到节点 u 的表示。这里抽取子图 的动机是节点对中心节点 u 的影响会随着最短距离的增加指数降低。而在节点分类问题中，一旦对节点进行编码，就可以学习任意一个函数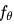将编码映射到类标签。G-META 利用 MAML 在一个新任务上用很少的样本学习该函数，在节点分类中利用节点级共享表征。

同样考虑了网络结构固定，但节点特征随任务变化的情况下的少样本节点分类问题。具体来讲，给定节点特征矩阵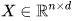 ，为第 t 个任务学习得到一个新的特征矩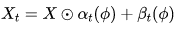，然后用GNN 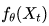学习第 t 个任务的节点表征。训练过程中，外层循环更新 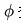参数，而 MAML 的内层循环只更新 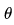参数，这使我们能够快速适应新任务。

图共享表征（Graph Level Shared Representation）

现在我们讨论全局的共享表征。图级表示的经典应用是图分类，而图分类通常需要大量的样本来进行高质量的预测。因此，使用少量标记图数据进行学习对于实际应用具有挑战性，这可以通过元学习来解决。现有的利用元学习进行图分类的论文通常先学习一种底层的共享表示，然后再将其用于新的任务。

Chauhan 在 ICLR 2020 上提出基于图谱度量的少样本分类方法。在元训练阶段，他们训练特征提取器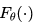 来从图中提取特征。在进行分类时，他们使用 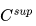来预测图的超类（super-class）概率，用注意力网络 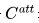来预测实际的类标签。在元训练阶段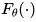， 和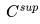 的参数被固定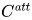， 将在新的类别上进行重新训练。由于特征提取器 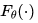是通用的共享结构，并且没有对测试任务进行再训练，因此该方法只需要从新类中获取少量样本。

尽管 Chauhan 针对图分类提出了一种新的图元学习结构，但该体系结构假定测试的超类结构和训练集之间有明显重叠，并且固定的特征提取器不能为新的任务更新。为此，Ma 提出了允许特征提取器有效地适应新的任务的元学习技术。他们使用两个网络嵌入层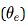，然后用分类层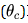对给定的图进行分类。但对于新任务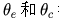， 都进行了更新。具体实现过程中，作者使用MAML 来更新参数，并使用基于强化学习的控制器来确定如何进行内层循环，如决定一个新任务的最佳适应步骤。

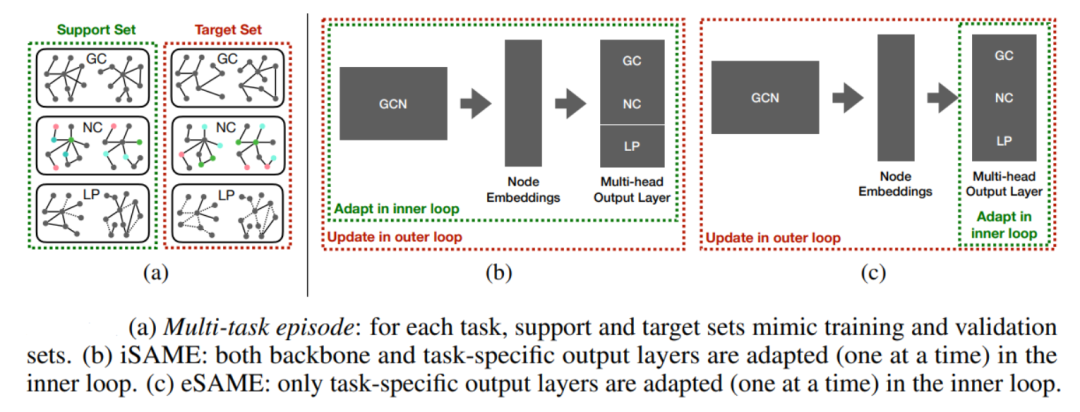
此外，发表于 NIPS 2020 workshop 的 SAME (Single-Task Adaptation for Multi-Task Embeddings) 尝试开发可以适应图分类、节点分类和链接预测三种不同任务的框架。类似于先前的工作，他们使用一个节点嵌入层生成节点嵌入并将图转换为表示，然后用多头输出层适应这三种类型任务。MAML 在初始化阶段训练节点嵌入层，在 MAML 内环中根据任务类型更新多头输出层。

6 未来方向

接下来，我们将讨论关于 meta-learning 和 GNN 的一些未来研究方向。

• 新兴应用：GNN meta-learning 的框架也可以考虑应用到其他相关问题上，例如交通预测、网络对齐、分子性质预测等。其中，在交通预测中，主要的挑战是对交通的复杂时空关联进行建模，并捕捉这些关联在不同位置的多样性。为此我们可以考虑如何应用元学习来学习这些相关性，并利用这些元知识在不同的地点进行高质量的预测? 而网络对齐旨在映射或链接来自不同网络的实体，这于跨域推荐等许多应用领域相关。然而现有的网络对齐方法难以规模化，一个有趣的研究方向是考虑用元学习来增强网络对齐的可伸缩性。

• 图组合优化：图组合优化问题在社交网络、医疗保健等许多领域都有应用。近期 GNN 也被用于解决该问题，这些基于 GNN 的方法在生成实际解集之前，需要生成候选解的节点/边。然而，在这些问题的解集中，每个节点重要性的标签通常很难得到，为此我们可以尝试使用元学习进行解决。此外，这些组合问题通常具有相似的结构，如影响最大化问题与 Max Cover 问题就有相似之处，因此我们可以借助元学习，在容易获得标签的“简单”问题上学习得到先验，然后将其用于解决较难获得标签的”困难“问题。

• 图挖掘问题：最近有一些尝试解决图挖掘问题的 GNN 框架，如确定两个图之间的相似度。为此，我们可以思考当相似度的概念发生变化，且没有足够的数据来通过标准的监督学习方法进行学习时，元学习是否有帮助? 另一个常见问题是检测两个输入图之间的最大公共子图(MCS)，它在生物医学分析和恶意软件检测中有广泛的应用。然而，MCS 计算是 NP-hard，并且最先进的精确 MCS 求解器不能扩展到大型图。为 MCS 问题设计基于学习的模型，同时尽可能少地使用标记 MCS 实例，仍然是一项具有挑战性的任务，而元学习可能有助于应对这一挑战。

• 理论基础：在 GNN 元学习的背景下，有两个重要的理论问题。一是如何理解迁移学习对 GNN 的帮助。二是确定共享表征的正确层次，弄清楚这种结构的表现力。并且由于用于元学习的 GNN 进一步限制了所使用的体系结构类型，所以我们需要考虑它是否会在表达性上带来任何额外的成本。

7 结语

本文对 GNN 和元学习的结合进行了全面的回顾。元学习在 GNN 中的应用是一个不断发展的领域，我们相信未来许多图问题将从这两种方法的结合中获益。

参考文献

[1] Debmalya Mandal, Sourav Medya, Brian Uzzi, Charu Aggarwal. “Meta-Learning with Graph Neural Networks: Methods and Applications." 

[2] Zemin Liu, Wentao Zhang, Yuan Fang, Xinming Zhang, and Steven CH Hoi. “Towards locality-aware meta-learning of tail node embeddings on networks”. In: CIKM. 2020, pp. 975–984. 

[3] Zemin Liu, Yuan Fang, Chenghao Liu, and Steven CH Hoi. “Relative and Absolute Location Embedding for Few-Shot Node Classification on Graph”. In: AAAI (2021). 

[4] Mingyang Chen, Wen Zhang, Wei Zhang, Qiang Chen, and Huajun Chen. “Meta Relational Learning for Few-Shot Link Prediction in Knowledge Graphs”. In: EMNLP-IJCNLP. 2019, pp. 4208–4217. 

[5] Davide Buffelli and Fabio Vandin. “A Meta-Learning Approach for Graph Representation Learning in Multi-Task Settings”. In: arXiv preprint arXiv:2012.06755 (2020).

 作者｜田长鑫

机构｜中国人民大学信息学院

研究方向 | 图表示学习和推荐系统

编辑：于腾凯

校对：林亦霖