- 1三教父神仙打架!AI瓶颈问题的三个解决方案!_如何改进人工智能的泛化瓶颈
- 2使用香橙派并基于Linux实现最终版智能垃圾桶项目 --- 上_香橙派 ir-keytable_香橙派 面试
- 3bert-textcnn实现多标签文本分类(基于keras+keras-bert构建)_textcnn+bert文本分类
- 4JSONView下载安装
- 5【计算机网络】UDP协议详解_udp端口
- 6医学影像数据集汇总(持续更新)150个_pmc-oa数据集下载
- 7【详解】神经网络矩阵的点乘与叉乘(pytorch版)_pytorch点乘与叉乘
- 8github:fork的用途_github fork
- 9GitHub 搜索技巧:如何更有效地搜索 issue、repo 和更多信息
- 10GO语言-方法_go语言 方法前面加go
基于Python的一元线性回归_一元回归建模 python
赞
踩
一元线性回归
1. 变量间的关系
自然界和社会经济中的事物或现象之间总是相互联系、相互依存、相互制约的,而反映这些联系的数量关系有两种:一种是函数关系,另一种是相关关系。
-
函数关系 是一种确定性关系,它是指当一个或几个变量取值一定时,另一个变量有确定的值与之对应,并且可以用函数描述出来。比如,某商品的销售收入I与该商品的销售量Q和销售价格之间P,可以这样表示:I=PQ。
-
相关关系 是一种非完全确定的关系,无法用确定的函数关系式表达。其特点在于变量之间在数量上确实存在着一定的内在联系,但这种在数量上的依存关系是不确定的,具有一定的随机性。
2. 回归分析
回归分析的主要研究对象是客观事物变量间的统计关系,是处理多个变量之间相关关系的一种数学方法。
在回归分析中,将一类变量视为解释变量,即自变量,而另一类变量视为被解释变量,即因变量。自变量可以是一个,也可以是多个,但因变量只能是一个。自变量只有一个时称为一元线性回归,自变量有两个及以上的回归分析称为多元回归分析。如果变量之间的关系为直线关系,称为线性回归,否则为非线性回归。
3. 一元线性回归模型
一元线性回归模型反映的是一个因变量
(
Y
)
(Y)
(Y)和一个自变量
(
X
)
(X)
(X)之间的线性关系,其一般形式为:
Y
=
β
0
+
β
1
X
+
ϵ
Y=\beta_0+\beta_1X+\epsilon
Y=β0+β1X+ϵ
上式中,
β
0
\beta_0
β0、
β
1
\beta_1
β1为待估参数,
ϵ
\epsilon
ϵ为随机误差项,通常假定
ϵ
∼
N
(
0
,
σ
2
)
\epsilon \sim N(0,\sigma ^2)
ϵ∼N(0,σ2) 。
下面通过例子来说明如何建立一元回归模型。
假设在某一社区中随机抽取了10个家庭研究其家庭收入与家庭食品支出的关系,得到表1的数据,试根据这些数据建立家庭食品支出和家庭收入
x
x
x之间的相关关系。
表1 家庭收入与食品支出(单位:百元)
| 家庭 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 家庭收入 | 20 | 30 | 33 | 40 | 15 | 13 | 26 | 38 | 35 | 43 |
| 食品支出 | 7 | 9 | 8 | 11 | 5 | 4 | 8 | 10 | 9 | 10 |
首先,以家庭收入为自变量,家庭食品支出为因变量,画出表1中家庭收入与食品支出数据的散点图
import matplotlib.pyplot as plt
import numpy as np
from pylab import *
x = np.array([20,30,33,40,15,13,26,38,35,43])
y = np.array([7,9,8,11,5,4,8,10,9,10])
mpl.rcParams['font.sans-serif'] = ['SimHei']
plt.scatter(x, y)
plt.xlabel("家庭收入")
plt.ylabel("食品支出")
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
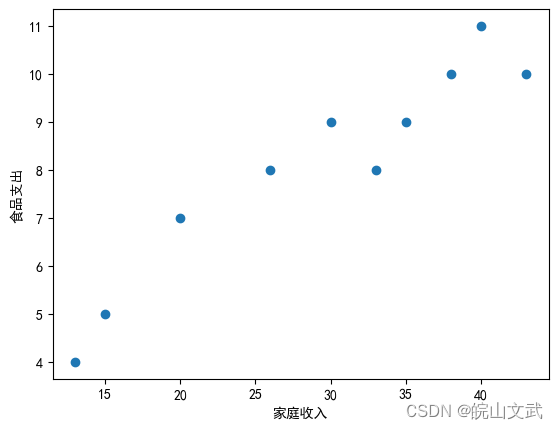
从散点图中可以看到这些点分布在某一条直线附近,也就是说
y
y
y和
x
x
x之间具有线性关系,但是这些点又不在同一直线上,所以
y
y
y和
x
x
x之间不存在确定的关系。这样,可以认为
x
x
x和
y
y
y之间的关系由两部分组成,一部分是由
x
x
x的线性函数
β
0
+
β
1
x
\beta_0+\beta_1 x
β0+β1x引起的,一部分是由随机因素
ϵ
\epsilon
ϵ引起的,即:
y
=
β
0
+
β
1
x
+
ϵ
y=\beta_0+\beta_1 x+\epsilon
y=β0+β1x+ϵ
这时y的数学期望
E
(
y
)
=
β
0
+
β
1
x
E(y)=\beta_0+\beta_1 x
E(y)=β0+β1x是x的线性函数,称y为x的一元线性函数。
若研究y与x之间的关系,在有n个样本观测点
(
x
i
,
y
i
)
:
i
=
1
,
2
,
…
,
n
{(x_i,y_i ):i=1,2,…,n}
(xi,yi):i=1,2,…,n的情况下,上式可写成如下形式:
y
i
=
β
0
+
β
1
x
i
+
ϵ
i
,
i
=
1
,
2
,
3
…
n
y_i=\beta_0+\beta_1 x_i+\epsilon_i, i=1,2,3…n
yi=β0+β1xi+ϵi,i=1,2,3…n
其中
ϵ
i
\epsilon_i
ϵi表示第i次观测时的随机误差,
ϵ
1
,
ϵ
2
,
ϵ
3
…
ϵ
n
\epsilon_1,\epsilon_2,\epsilon_3…\epsilon_n
ϵ1,ϵ2,ϵ3…ϵn相互独立,且
ϵ
i
∼
N
(
0
,
σ
2
)
\epsilon_i \sim N(0,\sigma^2 )
ϵi∼N(0,σ2)。
称上述两个公式为一元回归模型。
4. 基于Numpy.polyfit的线性回归
例如,使用 np.polyfit() 函数对 上面的 x 和 y 数组执行简单的线性回归 ( n = 1 ) 并绘制结果。 Python代码如下:
import numpy as np
x = np.array([20,30,33,40,15,13,26,38,35,43])
y = np.array([7,9,8,11,5,4,8,10,9,10])
import matplotlib.pyplot as plt
p=np.poly1d(np.polyfit(x, y, 1))
x_line = np.linspace(np.amin(x), np. amax(x), 200)
plt.scatter(x, y)
plt.plot(x_line, p(x_line))
plt.show()
print(p)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
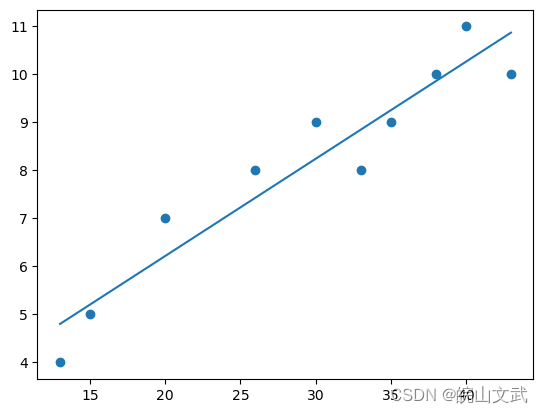
0.2023 x + 2.173
- 1
因此,使用 np.polyfit() 进行线性回归的结果是一条线性回归线 ( y(x) = a + bx ) 具有截距 a =2.173(精确值)和斜率 b =0.2023(精确值)。
所述 polyfit 模块是用于简单线性回归和度n的多项式回归非常有用的。但是,它没有给用户使用具有多个预测变量的线性回归的可能性,即多元回归。因此,不能将np.polyfit()用于混合交互项,而只能用于自交互项。此外,它没有给用户直接计算的可能性:决定系数 R 2 R^2 R2 评估拟合优度、Pearson 相关系数r、 假设检验的p值以及与回归系数相关的样本误差。
5. 基于Scipy的线性回归
SciPy 是一个 Python 库,代表Scientific Python。它是学术界和科学行业中最重要的科学计算库。该库包含几个用于特定目的的模块。在这些模块中,scipy.stats()模块是一般统计建模中最重要的模块。所述 scipy.stats()模块具有完全专用于线性回归子模块,其语法:scipy.stats.linregress()并使用最小二乘法作为最小化标准。
现在要查看 linregress 的运行情况,再次使用数组 x 和 y 如上所述,并使用以下Python代码:
import scipy as sp
reqr_results = sp.stats.linregress(x, y)
reqr_results
- 1
- 2
- 3
- 4
LinregressResult(slope=0.20229815542788027, intercept=2.172664045963108, rvalue=0.9509254640517752, pvalue=2.3910846120453154e-05, stderr=0.02327281362772548, intercept_stderr=0.7202174429436322)
- 1
从上面的 Python 代码可以看出,linregress 模块将线性回归的结果作为输出,其中:
斜率slope=0.20229815542788027,
截距intercept=2.172664045963108,
相关系数rvalue=0.9509254640517752,
p值pvalue=2.3910846120453154e-05,
斜率b的标准差stderr=0.02327281362772548,
截距a的标准差intercept_stderr=0.7202174429436322
linregress模块给出了线性回归的额外结果。 linregress唯一的缺点是不支持多元回归。它只支持简单的线性回归。此外,它没有为用户提供直接预测最小二乘法(如 scikit-learn库)中未使用的特征的新值的选项。
6. 基于statsmodel的线性规划
statsmodel库/模块模块非常灵活,它为用户提供了多种选项来执行特定的统计计算。
使用statsmodel 过使用上述 x 和 y 数组并使用最小二乘法作为 OLS 模块的最小化标准来执行简单的线性回归:
import statsmodels.api as sm
x = sm.add_constant(x) # 在简单线性回归公式中添加截距项
lin_model = sm.OLS(y, x)
regr_results = lin_model.fit()
#lin_y_pred = lin_model.predict(26)
regr_results.summary()
- 1
- 2
- 3
- 4
- 5
- 6
| Dep. Variable: | y | R-squared: | 0.904 |
|---|---|---|---|
| Model: | OLS | Adj. R-squared: | 0.892 |
| Method: | Least Squares | F-statistic: | 75.56 |
| Date: | Thu, 22 Feb 2024 | Prob (F-statistic): | 2.39e-05 |
| Time: | 22:50:14 | Log-Likelihood: | -9.9681 |
| No. Observations: | 10 | AIC: | 23.94 |
| Df Residuals: | 8 | BIC: | 24.54 |
| Df Model: | 1 | ||
| Covariance Type: | nonrobust |
| coef | std err | t | P>|t| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 2.1727 | 0.720 | 3.017 | 0.017 | 0.512 | 3.833 |
| x1 | 0.2023 | 0.023 | 8.692 | 0.000 | 0.149 | 0.256 |
| Omnibus: | 3.694 | Durbin-Watson: | 2.078 |
|---|---|---|---|
| Prob(Omnibus): | 0.158 | Jarque-Bera (JB): | 1.067 |
| Skew: | -0.113 | Prob(JB): | 0.587 |
| Kurtosis: | 1.416 | Cond. No. | 96.2 |
Notes:
[1] Standard Errors assume that the covariance matrix of the errors is correctly specified.
以下对报告参数进行解释:
Dep.Variable: 就是因变量,dependent variable,也就是咱们输入的y1,不过这里statsmodels用y来表示模型的结果。
Model:就是最小二乘模型,这里就是OLS。
Method:系统给出的结果是Least Squares,和上面的Model差不多一个意思。
Date:模型生成的日期。
Time:模型生成的具体时间。
No. Observations:样本量,就是输入的数据量,就是前面distance与loss中包含的数据个数。本例中为10
Df Residuals:残差自由度,即degree of freedom of residuals,其值= No.Observations - Df Model - 1,本例中结果为10-1-1=8。
Df Model:模型自由度,degree of freedom of model,其值=X的维度,本例中X是一个一维数据,所以值为1。
Covariance Type:协方差阵的稳健性,在本例中是nonrobust,这个参数的原理过于复杂,可以自行查询相关资料。不过在大多数回归模型中,完全可以不考虑这个参数。
R-squared:决定系数,其值=SSR/SST,SSR是Sum of Squares for Regression,SST是Sum of Squares for Total,这个值范围在[0, 1],其值越接近1,说明回归效果越好。
Adj. R-squared:利用奥卡姆剃刀原理,对R-squared进行修正,内容有些复杂,具体方法可自行查询。
F-statistic:这就是经常用到的F检验,这个值越大越能推翻原假设。
Prob (F-statistic):这就是上面F-statistic的概率,这个值越小越能拒绝原假设.
Log likelihood:对数似然。对数函数和似然函数具有同一个最大值点。取对数是为了方便计算极大似然估计,通常先取对数再求导,找到极值点。这个参数很少使用,可以不考虑。
AIC:其用来衡量拟合的好坏程度,一般选择AIC较小的模型,其原理比较复杂,可以咨询查找资料。该参数一般不使用。
BIC:贝叶斯信息准则,其比AIC在大数据量时,对模型参数惩罚得更多,所以BIC更倾向于选择参数少的简单模型。该参数一般不使用。
coef:指自变量和常数项的系数。
std err:系数估计的标准误差。
t:就是常用的t统计量,这个值越大越能拒绝原假设。
P>|t|:统计检验中的P值,这个值越小越能拒绝原假设。
[0.025, 0.975]:这个是置信度为95%的置信区间的下限和上限。
Omnibus:基于峰度和偏度进行数据正态性的检验,其常和Jarque-Bera检验一起使用。
Prob(Omnibus):上述检验的概率。
Durbin-Watson:检验残差中是否存在自相关,其主要通过确定两个相邻误差项的相关性是否为零来检验回归残差是否存在自相关。
Skewness:偏度。
Kurtosis:峰度。
Jarque-Bera(JB):同样是基于峰度和偏度进行数据正态性的检验。
Prob(JB):JB检验的概率。
Cond. No.:多重共线性的检验,即检验变量之间是否存在精确相关关系或高度相关关系。
在进行回归分析时,重点考虑的参数有R-squared、Prob(F-statistic)以及P>|t|的两个值,这4个参数是需要注意的,通过这4个参数就能判断的模型是否是线性显著的,同时知道显著的程度如何。
而在了解了summary之后,基本上就了解了线性回归的主要内容了。如果想要获取模型中的某些参数,其方法和在python中获取普通属性的方法一样,比如想要得到model1中的F检验数值和BIC数值,只需要输入model1.fvalue和model1.bic即可.
print(model1.fvalue)
print(model1.bic)
- 1
- 2
156.88615963321715
71.03747444412566
- 1
- 2
7. 基于scikit-learn的LinearRegression进行线性回归
scikit-learn 是用于机器学习的最佳Python库之一,适用于拟合和预测。它为用户提供了不同的数值计算和统计建模选项。它最重要的线性回归子模块是LinearRegression, 使用最小二乘法作为最小化标准来寻找线性回归的参数。
使用上述数组 x 和 y 进行简单的线性回归:
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
import numpy as np
if __name__ == '__main__':
x = np.array([20,30,33,40,15,13,26,38,35,43])
y = np.array([7,9,8,11,5,4,8,10,9,10])
#转换成numpy的ndarray数据格式,n行1列,LinearRegression需要列格式数据,如下:
X_train = np.array(x).reshape((len(x), 1))
Y_train = np.array(y).reshape((len(y), 1))
#新建一个线性回归模型,并把数据放进去对模型进行训练
lineModel = LinearRegression()
lineModel.fit(X_train, Y_train)
#用训练后的模型,进行预测
Y_predict = lineModel.predict(X_train)
#coef_是系数,intercept_是截距
a1 = lineModel.coef_[0][0]
b = lineModel.intercept_[0]
print("y=%.4f*x+%.4f" % (a1,b))
#对回归模型进行评分,这里简单使用训练集进行评分,实际很多时候用其他的测试集进行评分
print("得分", lineModel.score(X_train, Y_train))
#简单画图显示
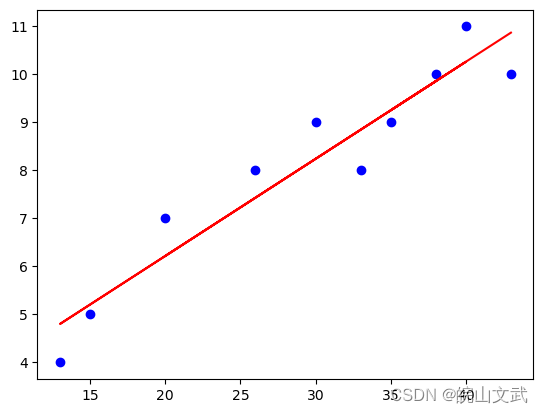
plt.scatter(x, y, c="blue")
plt.plot(X_train,Y_predict, c="red")
plt.show()
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
y=0.2023*x+2.1727
得分 0.9042592381820839
- 1
- 2