安全多方计算基础_两方保密计算功能函数

百万富翁问题

        Alice 拥有市值为x的公司，Bob拥有市值为y的公司。Alice和Bob都称自己是百万富翁。一天，Alice 和 Bob共同参加一个慈善捐款活动，两个人在聊天时都逐渐膨胀起来，Alice说自己肯定比Bob有钱，但Bob很快否定了Alice，他认为自己比 Alice更有钱。但出于对自己隐私信息的保护，Alice和Bob都不愿意透露自己的财产。那么Alice和Bob如何知道谁更富有呢？

        上面故事中的问题被称为是百万富翁问题，不论是使用对称加密算法还是公钥加密算法，通信双方中至少有一方的信息是可以被对方获知的。但是现实生活中存在这样一种情况：通信双方希望共同完成一种运算，但是又不希望对方获知自己的输入信息。直接使用对称加密算法或公钥加密算法都无法解决这个问题，为了解决这个问题，安全多方计算应运而生。

一、安全多方计算的概述

        安全多方计算（Secure Multi-party Computation,SMPC)是指在分布式环境下，多个参与者共同计算某个函数，该函数的输入信息分别由这些参与者提供，且每个参与者的输入信息是保密的；计算结束后，各参与者获得正确的计算结果，但无法获知其他参与者的输入信息。针对不同的应用场景，参与者所获得的计算结果可能是相同的，也可能是不同的。

        安全多方计算最早由图灵奖获得者姚期智提出。1982年，姚期智提出了著名的“百万富翁问题”，该问题实际上是安全多方计算的一个特殊应用。  “百万富翁问题”实际上是指如何在保护参与者输入信息的前提下比较参与者输入信息的大小。如果将这种比较运算扩展为任意函数，就是安全多方计算。

        1987年，Goldreich等人提出了可以计算任意函数的基于密码学安全模型的安全多方计算协议，从理论上证明了可以使用通用电路估值来实现所有安全多方计算协议。1998年，Goldreich对安全多方计算做了比较完整的总结，并提出了安全多方计算的安全性定义。国际著名密码学家Goldwasser曾经说过：“安全多方计算今天所处的地位正是公钥密码10多年前所处的地位。它是密码学研究中一个极其重要的工具，它在计算科学中的应用才刚刚开始，丰富的理论将使它成为计算科学中一个必不可少的组成部分。”由此可见，对安全多方计算进行研究是十分必要的。

        经过30年的研究，SMPC从当初的纯理论研究走到如今的现实应用。最近，越来越多新兴技术，如云计算、移动计算和物联网使得SMPC更加受到关注。这主要是因为，作为隐私数据计算的通用工具，在这些领域中，SMPC在解决安全性和隐私性方面有天然的优势。也因此出现了很多面向应用的SMPC协议。

---

        在 MPC 中，参与者，每个参与者的私有数据分别为 。参与者希望计算该私有数据上的公共函数的值：，同时对自己的输入保密。

        例如，假设我们有三方 Alice、Bob 和 Charlie，各自的输入 x、y 和 z 表示他们的工资。他们想找出三个薪水中最高的一个，但又不想互相透露每个人的收入。从数学上讲，这可以转化为计算：F(x, y, z) = 最大值(x, y, z)

        特别是，各方可以学到的只是输出和自己的输入。因此，在上面的示例中，如果输出为z，则 Charlie 得知他的z是最大值，而 Alice 和 Bob 得知（如果x、y和z不同），他们的输入不等于最大值，并且持有的最大值等于z。基本场景可以很容易地推广到各方有多个输入和输出，并且函数向不同各方输出不同的值。

通俗地说，多方计算协议旨在确保的最基本属性是：

输入隐私：无法从协议执行期间发送的消息中推断出有关各方持有的私有数据的信息。唯一可以推断出的有关私有数据的信息是通过单独查看函数的输出可以推断出的信息。

正确性：在协议执行期间愿意共享信息或偏离指令的敌对共谋方的任何适当子集都不应该能够迫使诚实方输出不正确的结果。这个正确性目标有两种形式：要么保证诚实方计算出正确的输出（“稳健”协议），要么在发现错误时中止（“带有中止”的 MPC 协议）。

        实际应用范围很广，从抛硬币等简单任务到电子拍卖（例如计算市场出清价格）、电子投票或隐私保护数据挖掘等更复杂的任务。一个典型的例子是百万富翁问题：两个百万富翁想知道谁更富有，但他们都不知道对方的净资产。这种情况的解决方案本质上是安全地评估比较函数。

---

二、计算模型

        安全多方计算的计算模型主要有基于“可信第三方”的计算模型、“交互计算”和“外包计算”三种。假设参与者集合为$P =\left \{ P_{1},P_{2},...,P_{n} \right \}$，对于$1\leq i\leq n$，每个参与者$P_{i}$只持有的秘密信息为$x_{i}$。使用安全多方计算，参与者所获得的输出集合$f\left ( x_{1},x_{2},...,x_{n} \right )= \left \{ f_{1}\left ( x_{1},x_{2},...,x_{n} \right ),f_{2}\left ( x_{1},x_{2},...,x_{n} \right ),...,f_{n}\left ( x_{1},x_{2},...,x_{n} \right ) \right \}$
其中$f_{i}\left ( x_{1},x_{2},...,x_{n} \right )$是参与者$P_{i}$的输出信息。

        下面用TrustServer 表示可信第三方，使用OutServer 表示外包计算模型中的外包服务器。

---

2.1.基于可信第三方的计算模型

        多个参与方为了安全地计算某个函数，可将自己的输入信息交给可信第三方，由可信第三方完成运算后将结果发送给各参与者。这种计算模型下的计算流程大致如下：

（1)对于$1\leq i\leq n$，参与者$P_{i}$将其秘密信息$x_{i}$发送给TrustServer。

（2)收集到所有参与者发送的秘密信息后，TrustServer计算$f\left ( x_{1},x_{2},...,x_{n} \right )$。

  (3)TrustServer 将$f_{i}\left ( x_{1},x_{2},...,x_{n} \right )$发送给$P_{i}$。

        计算结束后，参与者$P_{i}$得到$f_{i}\left ( x_{1},x_{2},...,x_{n} \right )$，TrustServer 得到$X= \left \{ x_{1},x_{2},...,x_{n} \right \}$和$f\left ( x_{1},x_{2},...,x_{n} \right )$。可以看出，TrustServer 通过计算过程可以获得全部秘密信息，信息的保密性由可信第三方来保证。然而，现实生活中很难找到这样一个可以完全信任的第三方机构。因此，这种方案不能满足实际的安全需求。在当前对安全多方计算的研究中，已经很少使用这种计算模型。

---

2.2.交互计算模型    

        交互计算模型是安全多方计算提出以来，使用最为广泛的一种计算模型。在交互计算模型中，各参与者互不信任，因此参考者不会将各自的秘密信息直接发送给其他参与者，也无须将保密信息交给第三方，而是由各参与者按照协议步骤通过交互计算共同完成函数运算。这种计算模型下的计算流程大致如下：参与者按照协议步骤执行计算，将协议要求的中间计算结果发给其他参与者及接受其他参与者发送的中间计算结果。

        计算结束后，参与者$P_{i}$得到$\left \{ f_{i}\left ( x_{1},x_{2},...,x_{n} \right ) ,VIEW_{i}\left ( x_{1},x_{2},...,x_{n} \right ) \right \}$

        其中$VIEW_{i}\left ( x_{1},x_{2},...,x_{n} \right )$表示参与者$P_{i}$在协议执行过程中得到的视图信息，主要包括$P_{i}$计算的中间结果和接收其他参与者发送的中间结果。可见信息的保密性由协议的安全性来保证。

---

2.3.外包计算模型

        外包计算模型是近几年来随着云计算技术的反展而逐渐引起学者重视的一种新型计算模型。在云计算环境中，参与者的本地计算能力非常有限，而云计算服务提供商以低廉的价格提供计算资源。但是出于对自己隐私信息的保护，参与者往往不希望直接将信息委托给云计算服务提供商，也不希望服务提供商得知计算结果。这种应用场景和安全多方计算不谋而合。因此，外包计算成为近几年来安全多方计算协议中经常使用的一种计算模式。参与者将自己的秘密信息经过一系列处理后外包存储在外包服务器上，当需要对所有参与者的秘密信息进行某种计算时，由外包服务器完成这些计算。当然，外包服务器在计算过程中可能需要和参与者进行必要的信息交互。

外包计算模型下的计算流程大致如下：

（1)对于$1\leq i\leq n$，参与者只对其秘密信息$x_{i}$，在本地进行计算处理得到$x_{i}^{'}$，然后将对发
送给OutServer。

  (2）收集到所有参与者发送的秘密信息后，OutServer调用可用的计算资源并通过和参与者的少量信息交互完成协议的运算。运算结束后，OutServer得到$f^{'}\left ( x_{1},x_{2},...,x_{n} \right )= \left \{ f_{1}^{'}\left ( x_{1},x_{2},...,x_{n} \right ),f_{2}^{'}\left ( x_{1},x_{2},...,x_{n} \right ),...,f_{n}^{'}\left ( x_{1},x_{2},...,x_{n} \right ) \right \}$

  (3)对于$1\leq i\leq n$，OutServer 将$f_{i}^{'}\left ( x_{1},x_{2},...,x_{n} \right )$发送给参与者$P_{i}$。参与者$P_{i}$在本地对
$f_{i}^{'}\left ( x_{1},x_{2},...,x_{n} \right )$进行简单的计算处理得到$f_{i}\left ( x_{1},x_{2},...,x_{n} \right )$。

        计算结束后，参与者$P_{i}$得到$\left \{ f_{i}\left ( x_{1},x_{2},...,x_{n} \right ) ,VIEW_{i}\left ( x_{1},x_{2},...,x_{n} \right ) \right \}$

        其中$VIEW_{i}\left ( x_{1},x_{2},...,x_{n} \right )$表示参与者$P_{i}$在协议执行过程中得到的视图信息，主要包括$P_{i}$计算的中间结果和接收OutServer 发送的中间结果。

        OutServer得到$\left \{ f_{i}^{'}\left ( x_{1},x_{2},...,x_{n} \right ) ,VIEW_{OutServer}\left ( x_{1},x_{2},...,x_{n} \right ) \right \}$，其中$VIEW_{OutServer}\left ( x_{1},x_{2},...,x_{n} \right )$表示 OutServer 在协议执行过程中得到的视图信息，主要包括OutServer 计算的中间结果和接收各参与者发送的中间结果。可以看出，信息的保密性由协议的安全性来保证。

---

三、安全多方计算的安全性定义

         非正式地说，MPC的目标是让一组参与者学习应用于他们的私人输入的某些商定函数的正确输出，而不会泄露任何其他内容。我们现在提供一个更正式的定义来阐明MPC旨在提供的安全属性。首先，我们提出了现实-理想范式，它构成了定义安全的概念核心。然后，我们讨论了两种不同的对手模型通常用于MPC。最后，我们讨论了组合问题，即当一个安全协议调用另一个子协议时，是否以自然的方式保持安全性。

---

3.1现实-理想范式

        定义安全性的一种自然方法是提出一种构成安全性违反的事情的“清单”。这不仅是一种乏味的方法，而且很麻烦且容易出错。不清楚什么时候可以认为清单是完整的。

        现实-理想范式通过引入一个“理想世界”完全避免了这个陷阱，这个“理想世界”隐含地捕获了所有的安全保证，并根据这个理想世界定义了安全。现实世界/理想世界范式提供了 MPC 复杂性的简单抽象，允许在其核心的 MPC 协议实际上是理想执行的假装下构建应用程序。如果应用程序在理想情况下是安全的，那么当运行真实协议时它也是安全的。

3.1.1理想世界

        在理想世界模型中，存在一个廉洁的受信任方，每个协议参与者都向该方发送其输入。该受信任方自行计算该函数并将适当的输出发送回各方。

3.1.2现实世界

        相反，在现实世界模型中，不存在可信方，各方所能做的就是相互交换消息。如果人们在现实世界中了解到的每一方的私人输入信息不会比在理想世界中了解到的更多，那么就可以说协议是安全的。在理想世界中，各方之间不交换任何消息，因此现实世界中交换的消息不会泄露任何秘密信息。

---

        安全多方计算的参与者分为诚实参与者、半诚实参与者和恶意参与者。在整个协议执行过程中，诚实参与者对协议完全“遵纪守法”，不存在提供虚假数据、泄露、窃听和中止协议的行为；半诚实参与者虽然会按照要求执行各个步骤，不存在提供虚假数据、中止协议等行为，但是他们会保留所有收集到的信息以便推断出其他参与者的秘密信息；恶意参与者完全无视协议执行要求，他们可能存在提供虚假数据、泄露他们收集到的信息、窃听甚至中止协议等行为。

        根据参与者的不同，安全多方计算的参与者模型分为半诚实模型和恶意模型。半诚实模型下，协议的参与者仅包含诚实参与者和半诚实参与者。如果恶意参与者参与协议的执行，则此类模型称为恶意模型。

3.1.3半诚实（被动）安全

        在这种情况下，假设受损方只是合作从协议中收集信息，但不偏离协议规范。这是一种幼稚的对手模型，在实际情况下安全性很弱。然而，达到这种安全级别的协议可以防止（否则合作的）各方之间无意中泄露信息，因此如果这是唯一的问题，那么它是有用的。此外，半诚实模型中的协议非常有效，并且通常是实现更高级别安全性的重要第一步。

3.1.3恶意（主动）安全

        在这种情况下，对手可能会任意偏离协议执行以试图进行欺骗。在该模型中实现安全的协议提供了非常高的安全保证。在大多数行为不端的一方的情况下：在不诚实多数的情况下，对手唯一能做的就是让诚实的一方在发现作弊行为后“中止”。如果诚实的各方确实获得了输出，那么他们就可以保证输出是正确的。他们的隐私始终得到保护。

---

        下面分别介绍半诚实模型、恶意模型下安全两方协议的形式化安全性定义。以此类推，可以得出安全多方计算的安全性定义。

        假设参与者$P_{1}$和$P_{2}$要计算函数$f:\left \{ 0,1\right \}^{*}\times \left \{ 0,1\right \}^{*}\mapsto \left \{ 0,1\right \}^{*}\times \left \{ 0,1\right \}^{*}$其中函数$f\left ( x,y \right )$的第一个元素为$f_{1}\left ( x,y \right )$，第二个元素为$f_{2}\left ( x,y \right )$。$\prod$是参与者$P_{1}$和$P_{2}$计算函数 f 的两方协议。

---

3.2半诚实模型下安全两方协议的安全性

   在协议$\prod$的执行过程中，参与者参与者$P_{1}$和$P_{2}$得到的信息分别记为$VIEW_{1}^{\Pi }\left ( x,y \right )=\left ( x,r^{1},m_{1}^{1} ,m_{2}^{1} ,...,m_{t}^{1} \right )$，$VIEW_{2}^{\Pi }\left ( x,y \right )=\left ( x,r^{2},m_{1}^{2} ,m_{2}^{2} ,...,m_{t}^{2} \right )$。其中，$r^{i}$表示$P_{i}$产生的随机数，$m_{j}^{i}$表示$P_{i}$接收到的第 j 个信息。协议$\prod$执行完后，参与者$P_{i}$的输出结果记为$OUTPUT_{i}^{\Pi }\left ( x,y \right )$。可以看出，$OUTPUT_{i}^{\Pi }\left ( x,y \right )$实际上是$VIEW_{i}^{\Pi }\left ( x,y \right )$中的一部分。

        对于确定性功能函数f，我们称协议$\prod$在半诚实模型下秘密的计算了 f 当且仅当存在概率多项式时间算法$S_{1}$和$S_{2}$，满足：

---

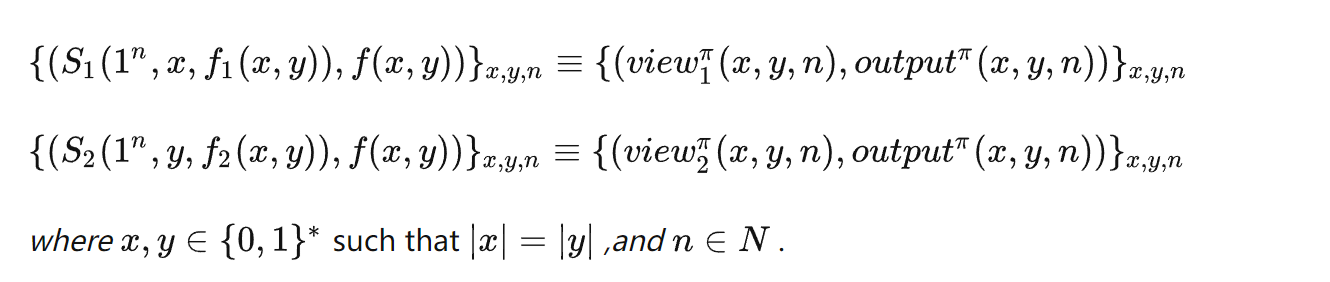
3.3.恶意模型下两方安全协议的安全性

3.3.1理想模型中的恶意攻击者

        在没有诚实多数(特别地,在我们这里考虑的两方情形)的情况下，一般不可能实现有保证的产出交付和公平。因此，这个"弱点"被纳入到理想模型中，允许理想执行中的对手中止执行或获得输出，而不需要诚实的一方获得其输出。参与者$P_{1}$和$P_{2}$，令 i ∈{ 1，2 } 定义被腐败者的指标，由敌手A控制.函数$f:\left \{ 0,1\right \}^{*}\times \left \{ 0,1\right \}^{*}\mapsto \left \{ 0,1\right \}^{*}\times \left \{ 0,1\right \}^{*}$的理想执行如下：

输入：令x表示参与方$P_{1}$的投入，y表示参与方$P_{2}$的投入。敌手A也有一个辅助输入，记为z。所有参与方在其安全参数磁带(包括被信任的一方)上以相同的值$1^{n}$初始化。

向信任方发送输入：诚实方$P_{j}$向信任方发送其规定的输入。受A控制的被破坏方$P_{i}$可以中止(通过用一个特殊的夭折消息来替换输入)，发送其规定的输入，也可以发送一些相同长度的其他输入给被信任方。这个决定是由A做出的，并且可能依赖于$P_{i}$的输入值和辅助输入z。表示( x′, y′) (注意到,如果 i = 2 ,则x′= x ,但y′不一定等于y ,反之亦然,如果 i = 1)发送给被信任方的一对输入。

提前中止选项：如果可信方收到某个i∈{ 1，2 }的形式中止的输入，则将中止发送给诚实方$P_{j}$，理想执行终止。否则，执行进入下一步。

信任方将输出发送给敌手：此时，可信方计算$f_{1}\left ( x^{'},y^{'} \right )$和$f_{2}\left ( x^{'},y^{'} \right )$，并将$f_{i}\left ( x^{'},y^{'} \right )$发送给$P_{i}$ (也就是说,它向腐败的一方发送其输出)。

敌手指示被信任方继续或停止：A发送继续或中止给被信任方。如果继续发送，可信方将$f_{j}\left ( x^{'},y^{'} \right )$发送给诚实方$P_{j}$。否则，如果A发送中止，则被信任方向$P_{j}$发送中止。

输出：诚实的一方总是输出它从可信的一方获得的输出值。腐败的一方什么也不输出。敌手A输出腐败方的指定输入、辅助输入z以及从被信任方获得的值$f_{i}\left ( x^{'},y^{'} \right )$的任意(概率多项式时间可计算)函数。

3.3.2在真实模型中执行

        我们考虑了一个实际的两方协议π被执行的真实模型(并且不存在可信的第三方)。在这种情况下，敌手A发送所有消息来代替腐败方，并且可能遵循任意多项式时间策略。相反，诚实的一方遵循π的指示。我们考虑一个简单的网络设置，其中协议在轮中进行，在每一轮中一方向另一方发送消息。(在多方设置中,这是一个不令人满意的模型,必须允许所有的参与方同时发送消息。然而,在这种情况下,标准是假设一个仓促的对手,意味着它在发送自己之前收到诚实当事人发送的消息。)

        设f如上所述，π是一个计算f的两方协议，意味着当P1和P2都诚实时，双方分别在输入x和y的情况下执行π后输出$f_{1}\left ( x,y \right )$和$f_{2}\left ( x,y \right )$。进一步，设A为非均匀概率多项式时间机，i∈{ 1，2 }为腐败方的索引。那么，π在输入( x , y)、辅助输入z到A和安全参数n上的真实执行，记为real π，A ( z )，i ( x , y , n)，定义为诚实方和敌手A从π的真实执行中得到的输出对。

3.3.3恶意模型下安全两方计算的安全性

        设 f 是一个两方函数，π是一个计算 f 的两方协议。协议π被称为在静态恶意敌手存在的情况下安全地计算 f ，如果对于实模型的每个非一致概率多项式时间敌手A，存在一个理想模型的非一致概率多项式时间敌手S，使得对于任意的i∈{ 1，2 }，协议π都能安全地计算 f 。

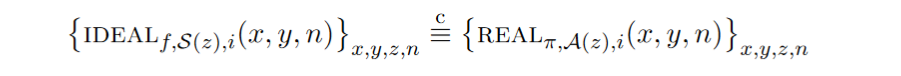
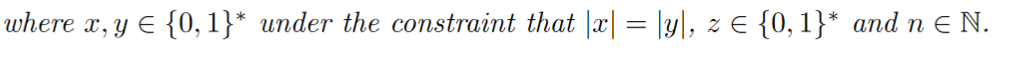
        上述定义假定当事人(和对手)知道输入长度(这可以从| x | = | y |是平衡的这一要求中看出,因此输入向量中的所有输入都是等长的)。我们注意到对输入长度的一些限制是不可避免的，因为在加密的情况下，这些信息在一定程度上总是被泄露。我们将忽略这一点，并仅仅假设功能是这样的，以至于各方知道所有输入的长度。

---

四、严格的安全性证明

        对于给定的密码学方案，如果已经给出了精确的安全性定义和明确的困难性假设，并不能说明这个密码学方案是安全的。如何证明某个密码学方案是安全的呢？“使用穷举法，利用目前已知的各种攻击手段对密码学方案进行攻击，如果所有这些攻击手段都无法攻破给定密码学方案，那么这个密码学方案就是安全的。”这看似是一种比较完备的证明手段但是通过这种方式证明为“安全的”密码学方案能否抵御未知的或未来提出的各种新型攻击方式呢？谁也不能给出肯定的答案，因为我们无法预知未来的攻击手段是什么样子的。另外，这种证明手段在效率上似乎会比较低，因为当前已知的攻击手段非常多。

        为了保证安全性，对于给定的密码学方案必须给出严格的安全性证明。可证明安全性理论(Provable Security）是现代密码学方案中广泛使用的一种证明方案安全性的形式化方法。形式化方法是指运用规范化的数学描述语言和形式推理，使用精确的数学手段和强大的分析工具进行计算机系统的分析。1978年，Needham和Schroeder 首次将形式化方法引入到公钥密码协议分析中。随后，众多学者投入到了密码学方案的形式化分析中。可证明安全理论是在预先确定的安全模型下，利用“规约”思想来分析协议安全性的形式化证明方法。Goldwasser等人首先提出了可证明安全理论的思想，并给出了相应的加密和签名方案。1979年，Rabin 使用可证明安全理论思想，基于求二次剩余困难性问题提出了一个加密方案。后来，Bellare 等人提出了著名的随机预言(Random Oracle，RO）模型方法论，将安全性证明从理论研究引入到了实际应用领域中。借助于可证明安全性理论，可以像进行数学定理证明那样对协议的安全性进行推理。该方法以计算复杂性理论为基础，首先确定密码学方案的安全目标，然后根据攻击者的能力选择适当的攻击模型，最后采用形式化的方法分析出攻破该方案的唯一方法是攻破某个数学困难性问题。通俗地讲，通过可证明安全性理论，将密码学方案的安全性规约到某个数学困难性假设。