- 1毕设项目:电影院售票管理系统(JSP+java+springmvc+mysql+MyBatis)
- 2linux shell读取命令行参数_shell脚本获取cli输入的参数
- 3Redis底层数据结构详解_redis数据结构
- 4ret2dlresolve超详细教程(x86&x64)
- 5Linux中如何快速切换目录_返回到当前目录的家目录
- 6Axure RP9基本操作_axurerp9 bilibili
- 7基于STM32的多功能智能手环设计(可以当做毕设与简历项目)_简历上智能穿戴项目描述
- 8聚类算法K-Means, K-Medoids, GMM, Spectral clustering,Ncut_partitioning methods: k-means and k-medoids algori
- 92022华为ICT大赛全国总决赛网络赛道实验解析及验证_华为ict国赛讲解
- 10八大排序时间复杂度与稳定性_各种排序方法的时间复杂度与稳定性
【5G NR】【一文读懂系列】移动通讯中使用的信道编解码技术-Viterbi译码原理
赞
踩
目录
一、引言
在数字通信领域,为了确保信息的可靠传输,我们常常需要对发送的数据进行编码,并在接收端进行译码。其中,Viterbi译码是一种广泛使用的最大似然序列估计算法,用于在存在噪声和干扰的通信信道中恢复原始数据。本文将详细介绍Viterbi译码的基本原理、应用场景、优缺点,并与其他译码技术进行比较。
二、Viterbi译码的基本原理
Viterbi译码算法是一种基于动态规划的最优路径搜索算法,它由Andrew Viterbi于1967年提出,最初用于卷积码的解码。Viterbi译码通过寻找最可能的发送序列来估计原始信息,即在所有可能的发送序列中,选择一条与接收序列差异最小的路径作为最优估计。
2.1 卷积码与网格图
在理解Viterbi译码之前,我们需要先了解卷积码。卷积码是一种纠错编码方式,它通过将输入数据与编码器的状态进行卷积运算来生成输出码字。卷积码的特点是可以利用历史信息,使得码字之间存在一定的相关性。这种相关性可以通过网格图来表示,网格图中的每一条路径都对应一个可能的发送序列。
2.2 Viterbi算法的核心思想
Viterbi算法的核心思想是在网格图中搜索最优路径。它按照时间顺序逐步计算每个状态的最优路径度量值,并保留到达每个状态的最优路径。在每一步中,算法都会根据当前接收到的符号和状态转移概率来更新路径度量值。最终,算法选择一条具有最小路径度量值的路径作为最优估计。
2.3 路径度量与状态转移
路径度量是衡量路径优劣的指标,通常定义为路径上所有分支的度量值之和。分支度量值可以根据接收符号与预期符号之间的差异来计算,差异越小,度量值越小。状态转移是指从一个状态转移到另一个状态的过程,每个状态转移都对应一个分支度量值。
三、Viterbi译码算法工作原理详解
Viterbi译码算法是一种最大似然序列估计(MLSE)算法,用于在存在噪声的情况下解码卷积码,它是由Andrew Viterbi在1967年提出的。该算法通过动态规划的方式,寻找最有可能通过卷积码编码器和噪声信道传输的原始信息序列。
3.1 算法流程
-
初始化:确定所有状态在时刻t=0的路径度量值。对于起始状态,路径度量通常设为0,而对于其他所有状态,路径度量则设为无穷大(表示不可能的状态)。
-
递推(路径度量计算与更新):对于每个时刻t和每个状态s,计算到达该状态的所有可能路径的度量值。路径度量通常基于接收序列和假设路径之间的差异,如汉明距离或欧氏距离。选择具有最小度量值的路径作为幸存路径,并更新路径度量和路径历史。
-
终止:在达到接收序列的末尾时,选择具有最小路径度量的状态作为最终状态。
-
回溯:从最终状态开始,沿着幸存路径回溯到初始状态,从而确定最可能的原始信息序列。
3.2 关键步骤
-
分支度量计算:对于每个状态和每个可能的输入比特,计算从当前状态转移到下一状态的分支度量。这通常涉及计算接收序列与假设分支之间的差异。
-
加-比较-选择(ACS)操作:对于每个状态,将所有进入该状态的路径的度量值相加,并与当前状态的幸存路径度量进行比较。选择具有最小度量值的路径作为新的幸存路径。
-
路径历史存储:为了能够在最后进行回溯,需要存储每个状态和时刻的幸存路径历史信息。
3.3 译码算法举例
维特比算法就是寻找一条路径,使得该路径的编码输出与接收序列的汉明距离最小,其关键就是路径的寻找过程。
- 根据网格图(Trellis)(【5G NR】【一文读懂系列】移动通讯中使用的信道编解码技术-卷积码原理),首先,我们从第一个状态出发,到下一个状态有两种路径,分别计算这两条路径的编码输出与接收序列的汉明距离(注意,此时不能进行任何舍弃,不能将距离大的舍弃)。

- 第二步,从第一步到达的两个状态出发,继续寻找路径,由于2位移位寄存器共有四种状态,因此此时我们得到到达所有状态的路径(无论是否最优)

- 第三步,从这四个状态出发,继续寻找路径,此时我们将得到8种路径。这一步是算法的关键,此时要保留到达各状态的最短路径,舍弃其他路径,即舍弃后仍保留四条路径,且四条路径分别对应四个状态(无论该状态以后的路径如何选择,当到达该状态时,该状态以前的路径一定是最优的)。对于(n,k,N)卷积码,进行维特比译码时,当到达第N步时,要对路径进行舍弃,只保留幸存路径的信息,储存幸存路径以及当前的累计距离。

- 第四步:继续进行路径寻找,同样只保留每个状态下的幸村路径,直至步数达到输入序列的个数。
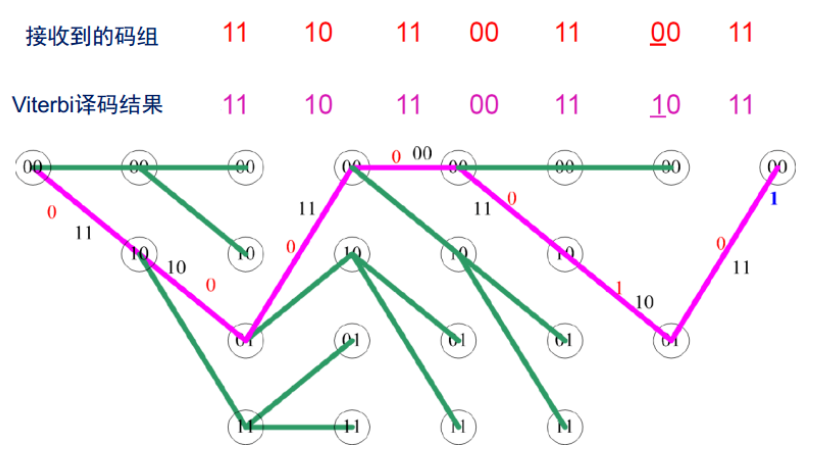
维特比算法复杂度:每步要比较2×2^(N-1)条路径(每个状态两条),计算量与步数(输入码的个数)成正比。
3.4 性能特点
-
最优性能:在给定足够长的接收序列时,Viterbi译码器能够提供最大似然序列估计,即它能够找到最有可能的原始信息序列。
-
复杂度:Viterbi译码的复杂度随约束长度的增加而指数增长。然而,通过有效的实现技术(如量化和剪枝),可以降低实际应用的复杂度。
-
延迟:由于Viterbi译码是一种块处理算法,它通常会在接收到整个块或一段足够长的序列后才开始解码,这可能会导致一定的解码延迟。
-
适用于多种信道:Viterbi译码不仅适用于加性白高斯噪声(AWGN)信道,还适用于其他类型的信道,如瑞利衰落信道和多径信道。
四、Viterbi译码的应用场景
Viterbi译码广泛应用于各种数字通信系统,特别是那些对误码率要求较高的场景。以下是一些典型的应用场景:
4.1 移动通信系统
在移动通信系统中,由于信道条件复杂多变,信号在传输过程中容易受到干扰和衰落。Viterbi译码可以有效地纠正由于信道干扰引起的误码,提高通信系统的可靠性。
4.2 卫星通信系统
卫星通信系统面临着长距离传输和大气层干扰等挑战。Viterbi译码结合其他纠错编码技术,可以在恶劣的信道条件下实现数据的可靠传输。
4.3 磁盘存储系统
在磁盘存储系统中,由于磁盘表面的缺陷、磁头的不稳定性以及外部干扰等因素,读取数据时可能会发生错误。Viterbi译码可以提高磁盘存储系统的数据恢复能力,减少读取错误的发生。
五、Viterbi译码的优缺点分析
5.1 优点
(1)性能优越:Viterbi译码是一种最大似然序列估计算法,它能够在存在噪声和干扰的信道中实现较低的误码率。
(2)适用于多种信道条件:Viterbi译码算法对信道条件的变化具有较强的适应性,可以应用于不同类型的信道。
(3)可与其他技术结合使用:Viterbi译码可以与其他纠错编码技术、调制技术等结合使用,进一步提高通信系统的性能。
5.2 缺点
(1)计算复杂度较高:Viterbi译码算法的计算复杂度随约束长度的增加而呈指数增长,这限制了其在一些实时性要求较高的场景中的应用。
(2)存储需求较大:为了实现Viterbi译码,需要存储大量的路径度量值和状态信息,这对硬件的存储能力提出了更高的要求。
(3)对初始状态敏感:Viterbi译码的性能受到初始状态选择的影响,如果初始状态选择不当,可能会导致译码性能下降。
六、Matlab算法示例
下面是一个简单的Viterbi译码算法的Matlab实现示例。请注意,这个例子假设你已经有了卷积码的生成多项式、输入信号(接收序列)以及其他必要的参数。
- function decoded_bits = viterbi_decoder(received_signal, constraint_length, generator_polynomials)
- % received_signal: 接收到的信号序列(1 x N 向量)
- % constraint_length: 约束长度(标量)
- % generator_polynomials: 生成多项式的矩阵形式(K-1 x R 矩阵,K是约束长度,R是输出数量)
- % decoded_bits: 译码后的比特序列(1 x (N/R) 向量,R是输出数量)
-
- % 参数检查
- if nargin < 3
- error('Not enough input arguments.');
- end
-
- % 初始化变量
- N = length(received_signal); % 接收信号长度
- R = size(generator_polynomials, 2); % 输出数量(速率为1/R)
- num_states = 2^(constraint_length - 1); % 状态数
- trellis = poly2trellis(constraint_length - 1, generator_polynomials); % 创建网格结构
-
- % 初始化路径度量和路径历史
- path_metrics = zeros(num_states, N/R); % 路径度量矩阵
- path_metrics(:, 1) = inf; % 初始化为无穷大
- path_history = cell(num_states, N/R); % 路径历史单元数组
-
- % 开始状态(全零状态)的路径度量和历史
- start_state = 0;
- path_metrics(start_state + 1, 1) = 0; % Matlab索引从1开始
- path_history{start_state + 1, 1} = start_state;
-
- % Viterbi算法主循环
- for t = 2:N/R
- for s = 0:num_states-1
- % 计算到达当前状态的所有可能的前一状态
- prev_states = viterbistate(trellis, s);
-
- % 对于每个可能的前一状态,计算分支度量
- for ps = prev_states
- branch_metrics = hammingdist(received_signal((t-1)*R + 1:t*R), ...
- encode(trellis, [path_history{ps + 1, t-1}, 0], 0, 'truncation', 'conventional')*2 - 1);
-
- % 计算路径度量并更新如果找到更好的路径
- metrics = path_metrics(ps + 1, t-1) + branch_metrics;
- if metrics < path_metrics(s + 1, t)
- path_metrics(s + 1, t) = metrics;
- path_history{s + 1, t} = ps;
- end
- end
- end
- end
-
- % 回溯找到最佳路径
- [~, end_state] = min(path_metrics(:, end));
- decoded_bits = zeros(1, N/R);
- for t = N/R:-1:1
- decoded_bits(t) = mod(end_state, 2); % 提取最后一位作为译码比特
- end_state = floor(end_state / 2); % 移除最后一位以回溯
- if t > 1
- [~, end_state] = ismember(path_history{end_state + 1, t}, 0:num_states-1); % 找到前一状态
- end
- end
-
- % 翻转译码比特序列,因为我们是从后向前回溯的
- decoded_bits = fliplr(decoded_bits);
- end
-
- % 注意:此代码片段是一个概念示例,可能需要针对您的特定应用场景进行调整。
- % 实际使用中,请确保所有输入参数都是正确和有效的,并考虑代码的边界情况和错误处理。
- % 此外,'encode' 函数用于模拟卷积编码过程,可能需要根据您的具体编码方案进行修改。
- % 代码中用到的 'hammingdist' 函数计算汉明距离,用于计算分支度量。如果您的信号不是二进制或者有不同的度量标准,请相应修改。

七、总结
Viterbi译码作为一种高效的纠错编码技术,在数字通信领域具有广泛的应用前景。它通过动态规划的方法在网格图中搜索最优路径,实现了在低信噪比和复杂信道条件下的可靠数据传输。卷积码和Viterbi算法在非常低的信噪比下性能不佳,复杂度随约束长度增加而增加;Turbo码是一种高级的前向纠错码,由两个或多个卷积编码器和一个随机交织器组成,使用迭代解码来逼近最大似然解码的性能,在较低信噪比下接近香农极限的性能。后续我们会介绍Turbo码原理和解码算法。
- 相关标签
Copyright © 2003-2013 www.wpsshop.cn 版权所有,并保留所有权利。


