李宏毅机器学习组队学习打卡活动day02---回归_crowdworker 机器学习

写在前面

报了一个组队学习的活动，今天的任务是机器学习中的回归，之前也学过一点，但是复习一遍当然更好

参考视频:https://www.bilibili.com/video/av59538266
参考笔记：https://github.com/datawhalechina/leeml-notes

回归

定义

什么是回归(regression)？
回归(regression)就是找到一个函数(使得误差最小的),然后输入数值x，可以得到一个数值Scalar。

举例：

• 股市预测(Stock market forecast)
  • 输入：过去10年股票的变动、新闻咨询、公司并购咨询等
  • 输出：预测股市明天的平均值
• 天气预测(weather forecast)
  • 输入：过去一个星期的天气状态、风向、云况等
  • 输出：预测明天的天气
• 邮件过滤(email fitering)
  • 输入：垃圾邮件的特性、文本的内容等
  • 输出：是否为垃圾邮件

模型步骤

• step1:模型假设，选择模型框架(线性模型)
• step2:模型评估，如何判断众多模型的好坏(损失函数)
• step3:模型优化，如何筛选最优的模型(梯度下降）

线性模型——一元线性模型：

一元线性模型类似于：$y=w\cdot x+b$，其中$w$和$b$可以不同。

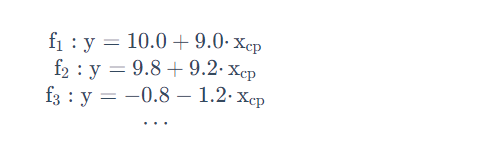
线性模型——多元线性模型：

多元线性模型类似于：$y=w_1\cdot x_1+w_2\cdot x_2+\cdots +w_n+x_n+b=\sum w_i{x}_i+b$
其中：

• $x_i$：表示各种特征(feature）
• $w_i$：表示各个特征的权重
• b: 偏移量

例如：宝可梦的CP(攻击力)的预测，其特征值与进化前的CP值、物种（Bulbasaur）、血量（HP）、重量（Weight）、高度（Height）等特征有关。

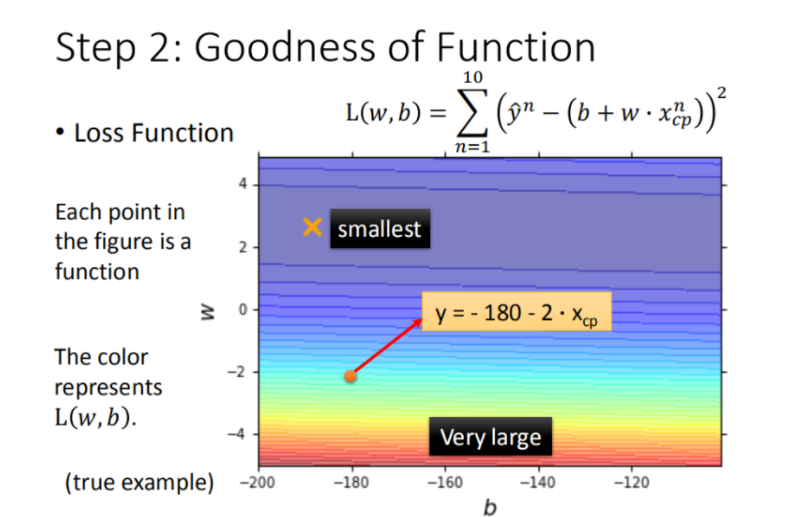
模型评估–损失函数

有了这些真实的数据，那我们怎么衡量模型的好坏呢？从数学的角度来讲，我们使用距离。求【进化后的CP值】与【模型预测的CP值】差，来判定模型的好坏。也就是使用损失函数（Loss function） 来衡量模型的好坏，统计10组原始数据的$((\hat{y}-y(\mathbf{x}){)}^2)$和，越小模型越好。如下图所示：

最终定义 损失函数 Loss function：
$\mathrm{L}(w,b)={\sum }_{n=1}^{10}({\hat{y}}^n-(b+w\cdot x_{cp}^n){)}^2$

将 ww, bb 在二维坐标图中展示，如图所示：

最佳模型-梯度下降

怎么调整w,b的参数，使得损失函数最小

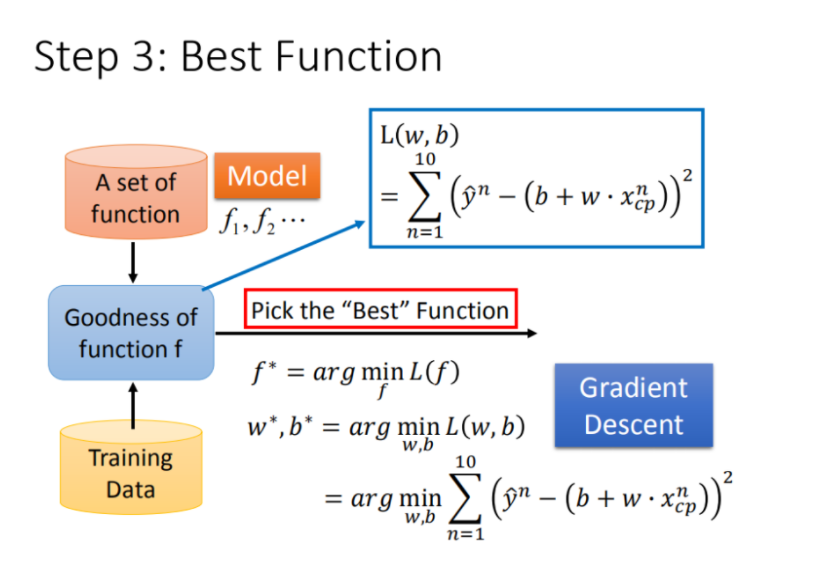
怎么计算w,b？

如果把 ww 和 bb 在图形中展示：

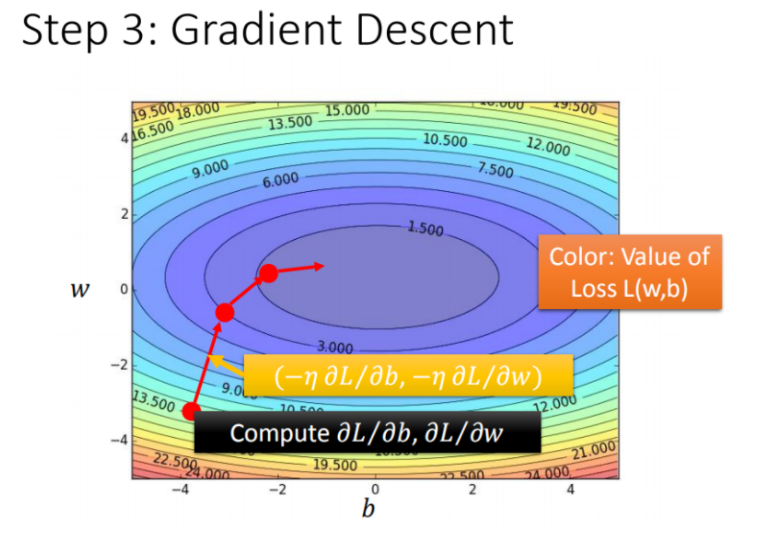
• 每一条线围成的圈就是等高线，代表损失函数的值，颜色约深的区域代表的损失函数越小
• 红色的箭头代表等高线的法线方向

面临挑战

• 问题1：当前最优（Stuck at local minima）
• 问题2：等于0（Stuck at saddle point）
• 问题3：趋近于0（Very slow at the plateau）

但是在线性模型中损失函数是凸函数，所以，梯度下降基本上都能找到最优点。

过拟合问题

每一个模型结果都是一个集合，5次模型包 $\supseteq$ 4次模型 $\supseteq$ 3次模型5次模型包$\supseteq$4次模型$\supseteq$3次模型 所以在4次模型里面找到的最佳模型，肯定不会比5次模型里面找到更差.

步骤优化

Step1优化：2个input的四个线性模型是合并到一个线性模型中

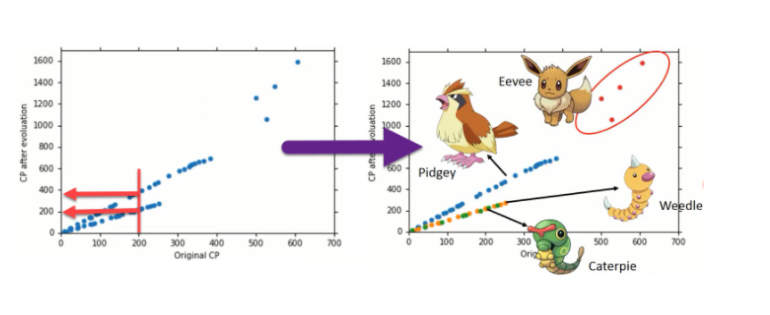
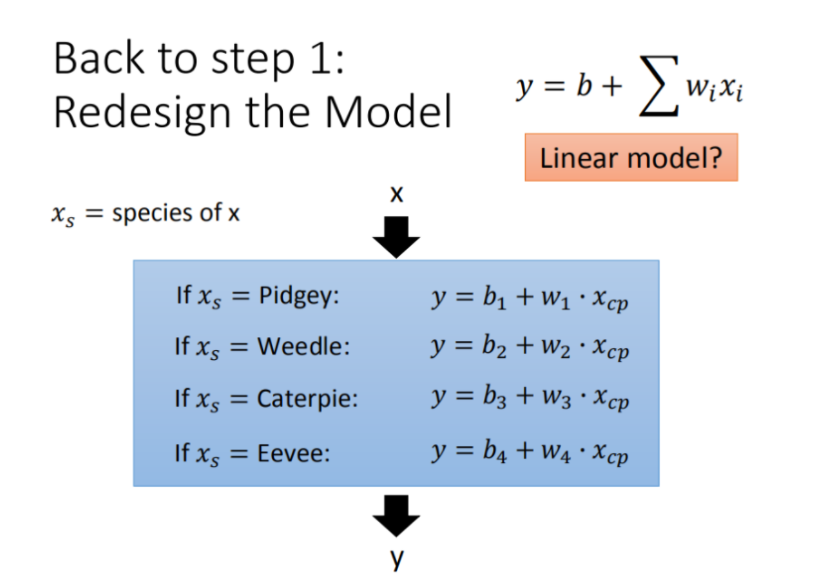
Step2优化：如果希望模型更强大表现更好（更多参数，更多input）

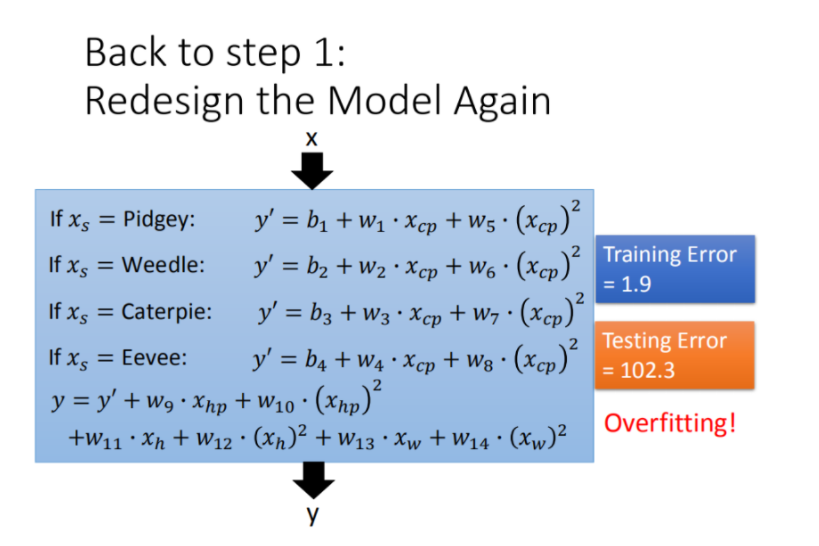
Step3优化：加入正则化

正则化是通过约束参数的范数使其不要太大，所以可以在一定程度上减少过拟合情况。

代码

# 导入所必须的库
import numpy as np
import matplotlib.pyplot as plt
import time
from pylab import mpl


plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文
mpl.rcParams['axes.unicode_minus'] = False

# 读取数据
file = open('data.txt')
X = []
Y = []
for fr in file.readlines():
    strs = fr.strip().split('\t')
    X.append(float(strs[1]))
    Y.append(float(strs[-1]))
x_d = np.asarray(X)
y_d = np.asarray(Y)

# 绘制
# fig = plt.figure()
# plt.scatter(X, Y)
# plt.show()

x = np.arange(0, 5, 0.05)
y = np.arange(0, 5, 0.05)
Z = np.zeros((len(y), len(x)))
R_X, R_Y = np.meshgrid(x, y)

# # # 计算loss
begin_b, begin_w = 0, 0
min_Z = 0X3f3f3f3f
for i in range(len(x)):
    for j in range(len(y)):
        b = x[i]
        w = y[j]
        Z[j][i] = 0
        for n in range(len(X)):
            Z[j][i] += (Y[n] - b - w * X[n]) ** 2
        Z[j][i] /= len(X)
        if min_Z > Z[j][i]:
            begin_b, begin_w = b, w
            min_Z = Z[j][i]

# Linear regression
# b = begin_b
# w = begin_w
b = 0
w = 0

lr = 0.000005
iteration = 1400000
b_history = []
w_history = []
loss_history = []
start = time.time()
for i in range(iteration):
    m = float(len(x_d))
    y_hat = w * x_d  +b
    loss = np.dot(y_d - y_hat, y_d - y_hat) / m
    grad_b = -2.0 * np.sum(y_d - y_hat) / m
    grad_w = -2.0 * np.dot(y_d - y_hat, x_d) / m
    # update param
    b -= lr * grad_b
    w -= lr * grad_w

    b_history.append(b)
    w_history.append(w)
    loss_history.append(loss)
    if i % 10000 == 0:
        print("Step %i, w: %0.4f, b: %.4f, Loss: %.4f" % (i, w, b, loss))

    if i > 3 and abs(loss_history[-1] - loss_history[-2]) < 1e-10:
        break
end = time.time()
print("大约需要时间：",end - start)

# plot the figure
plt.contourf(x, y, Z, 50, alpha=0.5, cmap=plt.get_cmap('jet'))  # 填充等高线
plt.plot([3.0077],[1.6953], 'x', ms=12, mew=3, color="orange")
plt.plot(b_history, w_history, 'o-', ms=3, lw=1.5, color='black')
plt.xlim(0, 5)
plt.ylim(0, 5)
plt.xlabel(r'$b$')
plt.ylabel(r'$w$')
plt.title("线性回归")
plt.show()

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91