神经网络基础原理（二）----分类问题（含Tensorflow 2.X代码）_神经网络解决分类问题

举线性回归的例子只是为了从最简单的角度来介绍神经网络的执行流程。神经网络在拟合线性函数方面的确存在得天独厚的优势。事实上，如果你对最优化理论熟悉，会发现神经网络的底层原理与最优化理论是一致的（目的都是求某一目标函数的极值）。

神经网络擅长的并不仅限于拟合线性函数。分类问题是神经网络最经典的应用之一。所谓的分类问题，是指给定m个学习样本，如何根据先验知识，将这m个样本分成k类。

解决分类问题第一步：数据建模

解决分类问题的第一步（也是其它经典问题的第一步），是数据建模。通常会把将这m个样本，根据其一些可量化的参数特征，或在计算机中的数字表示，转换成一个n维的特征向量。如将人的身高，体重，年龄转换成三维向量，将人划分成老人，年轻人，高个子，矮个子。其中身高，体重，年龄，都是可量化的。又如将猫的图片，根据其像素大小，红绿蓝三通道的数据转换成n*m*(r + g + b)维向量，其中n代表x轴方向的像素,m代表y轴方向的像素,r,g,b代表红绿蓝色深。

得到测试样本的特征向量，就可以把特征向量输入到神经网络中进行参数训练。

除了准备训练样本数据外，还需要根据人们的直观认识，或者人类社会中一些约定俗成的原则，来对训练样本预先进行分类。这个分类的过程，也称之为“打标签”的过程。在上例中，可以把1米8以上的人分类为高个子，BMI指数（体重与身高之商的平方）大于22的分类为胖子。

打标签的过程有人工打标的过程，也有机器打标的过程。但一般说到打标签都是指人工打标。因为如果能用机器打标，就根本不需要神经网络。所以打标签对于人们来说，也是一种额外的体力活。目前，所有经典问题的训练测试集都是人工标注的。

第二步：建立网络

前面我们介绍过一个最简单的一节点的单层神经网络是如何运作。事实上，上述运作机理可推广到n个结点。推广到n个结点的好处是能处理更多的参数值，从而逼近更复杂的函数。一般来说，叁数值的多少是跟自变量有关。自变量越多，参数就越多。举例3元一次函数f(x,y,z)=ax + by +cz ，就必须至少设置三个参数才能有效逼近。参数越多，神经网络能处理的信息就越多。注意！参数对应着是神经网络计算图里面结点与结点之间连接的边，而不是结点。计算图中的结点对应着一个计算。如上例中，要解决3元一次线性函数的模拟，也只是需要一个结点够了，因为从输出的三个变量到结点之间有3条边。

但分类问题并不是寻找一条直线（如果在n维空间中就是一个超平面）把所有结点都连起来。而是求k条线能把所有结点切分成k部分。虽然线性回归与分类问题不完全一样，但事实上，两者之间有异曲同功之妙。下图展示了线性回归与分类问题上的相似性。

                                                                                                                                   图1    线性回归

                                                                                                                             图2   二分类问题

 

聪明的读者可能会发现，两者没有本质上的区别，只是模拟的直线偏转了一点而已。也就是说从本质上说，两者是没有任何区别。另外，我们知道在平面几何中（这结论可以推广到n维空间）一条直线，可以把平面直角坐标系划分成两个部分，k条互不重合的直线理论上就可以划分出至少k部分。前面解释过在神经网络计算图中，一个结点代表一个线性函数（或称一个计算），k条线就是k个结点。因此神经网网络中的结点数量，代表着神经网络模拟函数（不仅限于线性函数，下面会介绍）的能力。越多的结点，神经网络拟合出来的函数个数就越多。同理，我们知道1层的网络相当于求f(x)，2层的网络就相当于求f’(f(x))，所以神经网络的层数越多，神经网络拟合的函数就越复杂。当我们发现1层网络函数表达能力有限，不能很多地划分样品的时候，就可尝试增加层数，来模拟更复杂的函数。虽然从问题的规模大概可以推断出网络至少需要多少个参数或多少个结点，但从目前学术界的研究现状来看，网络结点的数量和层次更多的取决于经验。

神经网络的结点不是越多越好，网络层次结构也不是越多越好。这完全取决于问题的规模和性质。举例，对于分类问题而言，至少需要一个有n个输入，有1个含q个神经元的隐层的全连接神经网络。这样输入层的权重参数至少有n*q+q个。输入经过隐层的变换，也由一个n维向量，变成一个q维向量。因此，需要有另外一个输出层来将结果转换为k维的输出，以匹配人工标注的标签集。因此，一个含一个隐层和一个输出层的稍为复杂的神经网络是下面这个样子的。

 从图中可以看到每个输入到每个神经元之间都有一条边，而每边条都一个权重。对于隐含层的第i神经元而言，其输出为

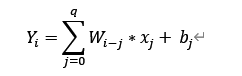
如果把所有输出组合成一个一维向量O=[Y1 ，Y2，Y3……]，那么眼尖的读者马上就会发现这个一维向量Y，刚好就等于 输入n维向量X 与n * q维的权重向量W的笛卡尔积，再加上q维的偏置向量。即:

这个公式非常眼熟，没错，这正是前面讨论过的线性函数。虽然这里的运算已经变成了矩阵运算，但线性函数的很多重要性质，并没有发生根本性的变化。

另外，要将q维的隐含层输出转换成目标的k维数据，还要使用一层额外的输出处理层。常用于分类的输出层为softmax输出层。

这里先简单介绍一下softmax函数。由于隐层输出Y不一定是一个概率分布向量，也就是说Y向量各维相加的结果不一定等于1。为了将Y转换为概率分布向量，因此定义softmax函数：

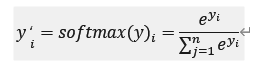
容易看出，可以用来描述样本分类的概率分布问题。有人可能会问，为什么不直接把输出函数定义成：

这样不是也可以达到效果吗？

这就跟后面的计算损益有关了。对于分类问题而言，我们知道一个样本会对应着某一个标签t。如果把对样本被分类成某个分类t，看成是一个随机事件的话，那么这个随机事件就相当于一个概率函数q(x)。

下面介绍一个信息论的重要概念---交叉熵。交叉熵刻画的是两个概率分布的距离。对于两个随机事件的概率分布p和q而言，如果两个随机事件存在一定的关联关系，那么可以通过交叉熵来描述彼此相关联的程度：

若神经网络认为输入X被归类为t的概率为p(也称为置信度),那么q就可以认为是X被人归类为t的概率。举例，对于一张画有猫的图片中，神经网络认为这张图片画的是猫的概率q=0.991，那么人给出的概率就是p=1。那么交叉熵H=- 1 * log0.991≈0。显然交叉熵越小，用q(x)来近似表达p(x)的能力就越强，神经网络对样本的分类能力就越接近人。目前，基于交叉熵的损失函数已被广泛应用于分类问题上。

回到前面的问题，为什么不将输出层softmax函数定义得简单一点呢？事实上把softmax函数定义成自然对数指数的形式，正是为了方便对交叉熵进行逆向求导。如果把softmax函数代入交叉熵公式，可得如下公式：

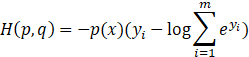
显然，对这个公式求某一个yi 的偏导要简单得多。现在我们来求它的偏导可得：

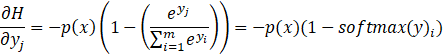
这就是为什么要把softmax函数定义成自然对数的指数次幂的形式的原因。

非线性化与激活函数

到此，已经基本把用于分类问题的神经网络的网络结构以及基本的数学原理都介绍完了。但事实上，上面介绍的只是最基本的神经网络。而这一类神经网络又被称为感知机。感知机是最弱的神经网络模型，只能解决线性可分的问题。所谓的线性可分，是指样本可以被一条直线或一个线性多维超平面分开。它甚至不能解决逻辑运算的异或问题。

举例，假设存在这样的训练集([1,0],1),([0,1],1),([1,1],0),([0,0],0)（本质上是一个异或运算的真值表）。现在希望神经网络能训练出一个线性函数，能对这个训练集的数据进行很好的拟合。

按照前面介绍过的算法，先假设存在一个这样的线性函数f(x,y)=ax+by+c，把测试样例代入得到下面这组方程：

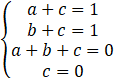
很明显这是一个矛盾方程。这就从一个侧面印证了线性函数不能拟合逻辑代数中经常出现的异或运算。虽然实际的证明比这个示例复杂得多，但感知机表述能力的局限性早在上个世纪80年代被人们所证实。这也导致神经网络的研究在很长一段时间陷入低迷的状态。

既然线性函数是有缺陷的，那就让神经网络模拟出非线性的函数。要让神经网络演化出非线性函数的能力，最简单直接的办法，就是改变计算结点函数的定义。这个非线性的函数就是所谓的激活函数。常见的激活函数有ReLu(Rectified Linear Unit),sigmod,tanh等。ReLu函数相当于一个符合函数，只有当x > 0时，y才等于x。sigmod能把输出变成0-1之间的一个小数值。 tanh多见RNN网络。

为什么加入了激活函数，神经网络模拟出来的函数就能表现非线性化的特点？首先，我们先了解下什么叫线性函数。线性函数的第一大特征就是函数的导数或偏导数在整个定义域中处处相等。但激活函数，以ReLU为例，显然对于x>0和x<0以言，它们的导数并不处处相等。其次，众所周知，线性函数有下述两种特殊的性质：

显然，上述提到的众多激活函数都不具备这样的性质。

下面我们就以神经网络最常用的Relu激活函数为例，介绍激活函数是如何解决上述提到的异或问题。ReLu函数的表达式为ReLU(x)=max(0,x)。

要解决上面的问题，首先我们需要两个独立的函数和一个用于归并结果的输出函数。

其中一个函数为f(x)=ReLU(ax+by+c), 另外一个为f’(x)=ReLU(px+qy+k)。另外还需要一个总的输出函数Y=m*f(x)+t*f’(x)。想达到异域运算的效果，可以令f(x)的目标输出值为([1,0],1),([0,1],1),([1,1],2),([0,0],0)。令f’(x)= ([1,0],0),([0,1],0),([1,1],1),([0,0],0)。Y的输出值刚好是异域运算的结果。

由于篇幅有限，这里就不演算神经网络训练的过程。通过肉眼观察，其实可以直接得出a=1,b=1,c=0，p=1,q=1,k=-1，m=1,t=-2是满足上述要求的一个有效解（具体的验算过程，由于篇幅有限，请读者自行代入验证），这证明通过上述办法，是可以得出满足异或运算规律的表达式。但线性函数不管怎样进行排列组合，根据线性函数的性质，最后归演出来的函数，永远都是线性函数。如上例，如果把激活函数去掉，归演出来的输出函数Y=m * (ax + by + c ) + t * (px + qy + k)= (ma + tp) * x + (mb + tq) * y + mc + tk = a’x + b’y + c’，结果还是一个线性函数。而前面已经证明过线性函数是模拟不了异或运算的。

从上面的推导，不难看出解决异或问题的神经网络是长成下面这个样子的：

仔细的读者会发现，这个神经网络正是前面提到的全连接单 层神经网络的一个特例。

 

代码实现（为了简化代码，下面的代码使用高层API keras来编写）：

# 模拟异或运算的神经网络模型

import tensorflow as tf

 

# 初始化样本数据

x=tf.convert_to_tensor([[1,0],[0,1],[1,1],[0,0]])

# 初始化标签数据

y=tf.convert_to_tensor([1,1,0,0])

#  测试样本，测试样本只是稍为加了点噪音和打乱了一下顺序而已,理想的目标预测值为[0,1,0,1]

x_=tf.convert_to_tensor([[1.0000006,1.00000008],[1.000006,0.00000001],[0.000000003,0.0000000001],[0.0000004,1.0000005],])

 

 

#  设计两层神经网络，第一层隐含层共2个结点，激活函数为RELU;第二层为输出层仅包含一个结点，不设置激活函数

model = tf.keras.models.Sequential([

  tf.keras.layers.Dense(2, activation='relu',input_shape=[2]),

  tf.keras.layers.Dense(1)

])

 

#  定义优化器，用于优化学习率等超参数指标

optimizer = tf.keras.optimizers.Adadelta(lr=1.0, rho=0.95, epsilon=1e-06)

 

#  编译模型，loss='mse'指定损失函数为均方标准差，Metrics标注网络评价指标mse为标准差,accuracy为准确率

model.compile(loss='mse',

                optimizer=optimizer,

                metrics=['mse','accuracy'])

 

#  打印网络参数模型，仅用于自检

model.summary()

 

#  重复训练1000次

for i in range(1000):

       #  输入样本x和标签y, batch_size=1，因为样本数量少，每输入1条数据，就运行反向传播算法，更新网络参数。

       model.fit(x=x,y=y,batch_size=1)

 

#  打印模型的预测值，检验模型的预测能力

print(model.predict(x_))

 

下面是Tensorflow输出的结果：

4/4 [==============================] - 0s 1ms/step - loss: 3.4736e-04 - mse: 3.4736e-04 - accuracy: 1.0000

4/4 [==============================] - 0s 2ms/step - loss: 2.8554e-05 - mse: 2.8554e-05 - accuracy: 1.0000

[[1.8305626e-02]

 [1.0095160e+00]

 [8.3606783e-04]

 [9.9998516e-01]]

 

这里对结果稍作解释，虽然模型的目标输出为[0,1,0,1]，但事实上，模型对训练样本的准确率已经达到了100%。尽管预测出来的数据已经很接近目标输出，但还是有一点误差。这些误差来源于两个原因。其一，是计算机的计算精度有限。由于上述代码是在本人的PC上面跑的，而且用的还是不太擅长浮点运算的CPU来跑，跑出这样的结果也是意料之中。其二，神经网络有所谓过拟合的问题。所谓的过拟合，就是指拟合训练数据的效果很好，但模型预测能力却很弱。过拟合问题的成因有多种，其中样本数太少，也是一个重要的原因。在上例中，只输入了4个训练样本进行训练，极有可能已经出现了过拟合现象。

另外，还要额外注意的一点是，本文出现的测试结果并不具备重复性。也就是同一段代码，在不同的机器上面跑，出来的结果有可能是完全不一样的。这是因为Tensorflow在建立神经网络的时候，会自动随机初始化网络参数。网络参数初始化的质量好不好，也会直接影响神经网络的收敛速度。如果系统把参数一下子就初始化到了最优解附近，可能多迭代几次就已经达到最优了。相反，如果参数初始化到了山顶，下坡的速度就会慢很多。所以神经网络训练，还带有一点运气的成分。但总体来说，随着梯度下降算法的不停应用，神经网络还是会往着（局部）最优解的方向前进。