【数据结构】二叉树的相关操作以及OJ题目

1. 二叉树

当一个树不是满二叉树或完全二叉树时，它是不适合使用数组存储的，它应该使用链式结构来存储。
再看二叉树基本操作前，再回顾下二叉树的概念，二叉树是：

1. 空树
2. 非空：根节点，根节点的左子树、根节点的右子树组成的。

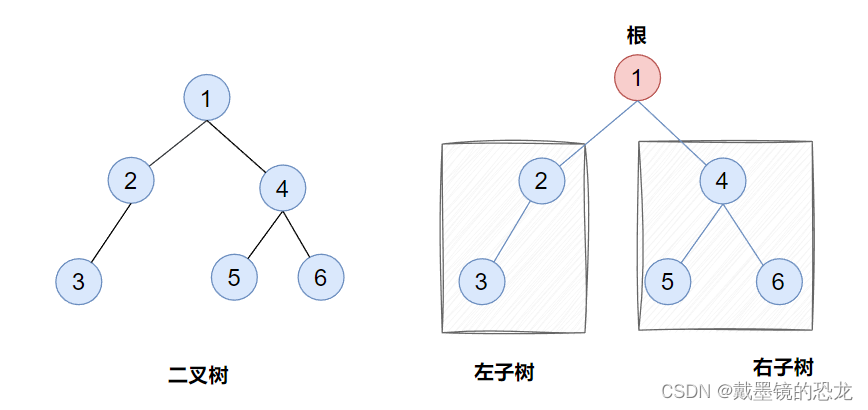
从概念中可以看出，二叉树定义是递归式的，因此后序基本操作中基本都是按照该概念实现的。
所以可以定义成下面这种：

typedef int TNDataType;
typedef struct TreeNode
{
	TNDataType val;
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;
1
2
3
4
5
6
7

2.二叉树的遍历

所谓二叉树遍历(Traversal)是按照某种特定的规则，依次对二叉树中的节点进行相应的操作，并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历是二叉树上最重要的运算之一，也是二叉树上进行其它运算的基础。

按照规则，二叉树的遍历有：前序/中序/后序的递归结构遍历：

1. 前序遍历——访问根结点的操作发生在遍历其左右子树之前。 （根左右）
2. 中序遍历——访问根结点的操作发生在遍历其左右子树之中（间）。（左根右）
3. 后序遍历——访问根结点的操作发生在遍历其左右子树之后。（左右根）

2.1前序遍历

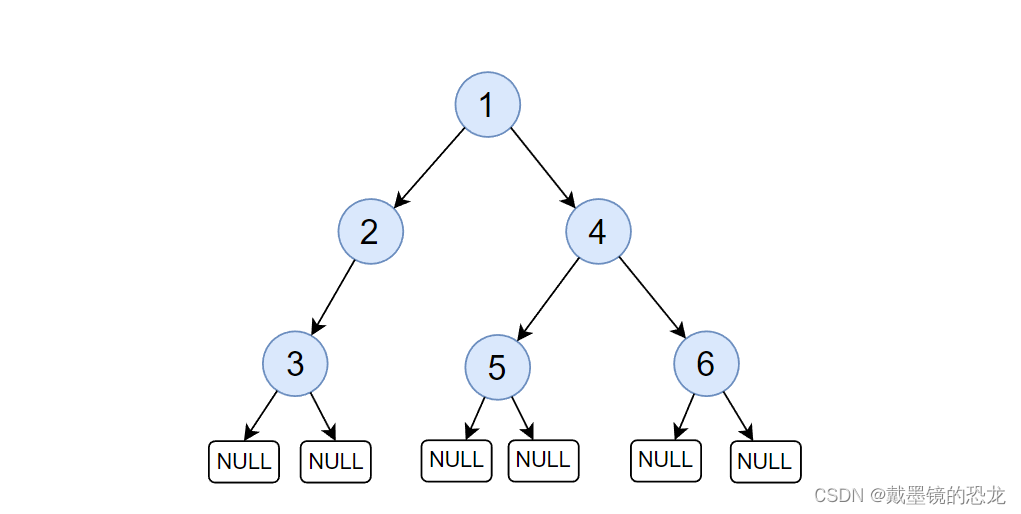
前序遍历：先访问树的根，然后访问左子树（左子树又被分为根、左子树、右子树，直到左子树不能拆分），然后再访问右子树（右子树又被分为根、左子树、右子树，直到右子树不能拆分）

先遍历根（有根一直根），然后左（有左一直左），最后右，拆分了以后就从头来

遍历结果	1 2 3 NULL NULL NULL 4 5 NULL NULL 6 NULL NULL
谁的NULL:      3    3    2        5    5      6    6
1
2

void PreOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	printf("%d ", root->val);//先遍历根

	PreOrder(root->left);//然后遍历左子树

	PreOrder(root->right);//最后遍历右子树
}
1
2
3
4
5
6
7
8
9
10
11
12
13

2.2中序遍历

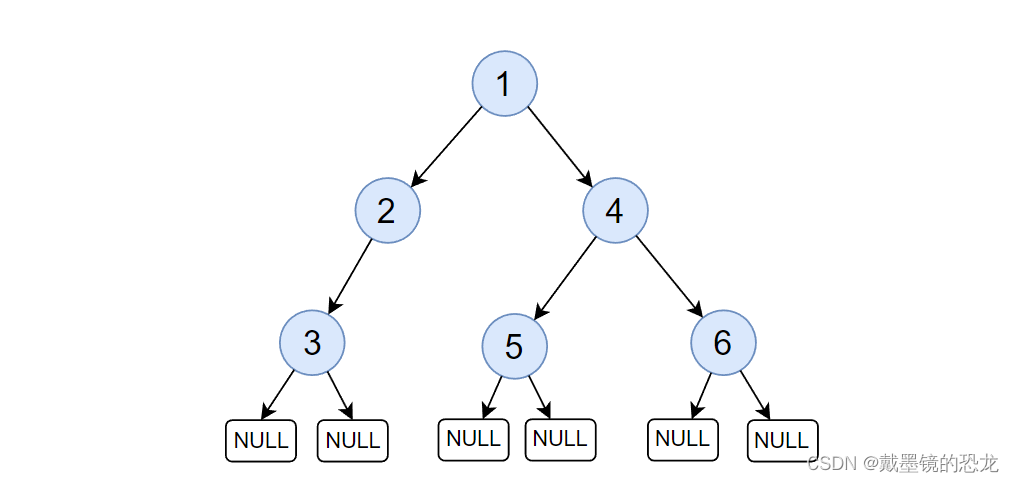
中序遍历：有左子树就一直访问左子树，直到左子树不能再拆分，然后遍历根，最后遍历右子树（右子树又拆分为根、左子树、右子树。也得先访问左子树）

有左一直左，然后根，最后右，拆分了以后就从头来

遍历结果: NULL 3 NULL 2 NULL 1 NULL 5 NULL 4 NULL 6 NULL
谁的NULL: 3       3      2      5      5      6     6
1
2

void InOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}
	InOrder(root->left);//先遍历左子树

	printf("%d ", root->val);//再遍历根

	InOrder(root->right);//最后遍历右子树
}
1
2
3
4
5
6
7
8
9
10
11
12
13

2.3后序遍历

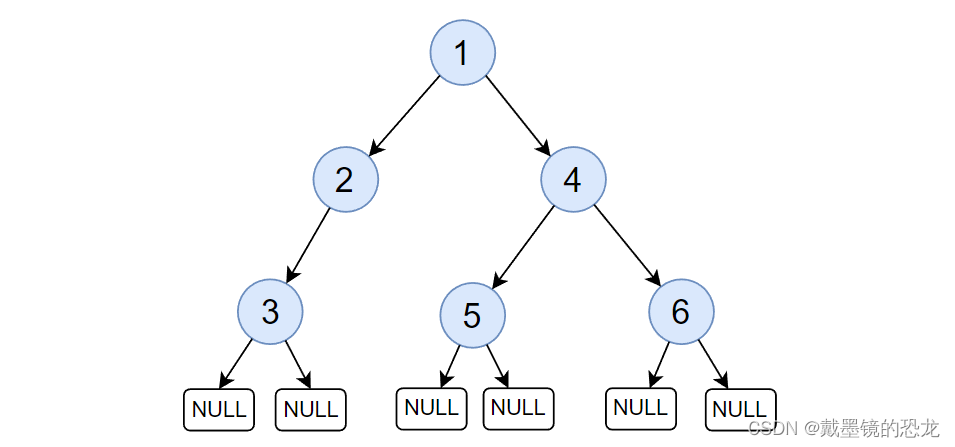
后序遍历：先遍历左子树（左子树又拆分为：根、左子树、右子树），然后遍历右子树（右子树又拆分为：根、左子树、右子树），最后遍历根。
有左一直左，然后右，最后根，拆分了以后就从头来

遍历结果: NULL NULL 3 NULL 2 NULL NULL 5 NULL NULL 6 4 1
谁的NULL:  3    3      2      5    5      6    6  
1
2

//后序遍历
void PostOrder(TreeNode* root)
{
	if (root == NULL)
	{
		printf("NULL ");
		return;
	}

	PostOrder(root->left);//先遍历左子树

	PostOrder(root->right);//再遍历右子树

	printf("%d ", root->val);//最后访问根
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

2.4层序遍历

二叉树的层序遍历需要借助队列实现。
首先需要将根入队列，然后再出队列，出队列时，需要将自己的孩子带进队列之中。由于栈先进先出的特点，只有上一层全部出完了才会出当前层，故可以实现层序遍历。

需要注意的是：链表的数值域设置为指向树节点的指针

//树的结构
typedef int TNDataType;
typedef struct TreeNode
{
	TNDataType val;
	struct TreeNode* left;
	struct TreeNode* right;
}TreeNode;


//链表的节点
typedef TreeNode* QNodeDataType;//将链表的数值域设置为指向树节点的指针
typedef struct QueueNode
{
	QNodeDataType data;
	struct QueueNode* next;
}QNode;
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

//层序遍历
void TreeLevelOrder(TreeNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		//出数据
		TreeNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			printf("%d ", front->val);
			//出的数据将其孩子带进队列中(带下一层)
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			printf("N ");
		}
	}
	printf("\n");
	QueueDestroy(&q);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

3.树的节点个数

方法：当前节点只加自己，然后再加上左子树和右子树中节点的个数

int TreeSize(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	return 1 + TreeSize(root->left) + TreeSize(root->right);
}
1
2
3
4
5
6
7
8

4.树的高度

当前层加上子树中高度大的一个

int  TreeHeight(TreeNode* root)
{
	if (root == NULL)
	{
		return 0;
	}
	int left = TreeHeight(root->left);
	int right = TreeHeight(root->right);
	return  left > right ? left + 1 : right + 1;
}
1
2
3
4
5
6
7
8
9
10

5.叶子节点的个数

是叶子，返回1；不是叶子，继续遍历左右子树，空树返回0

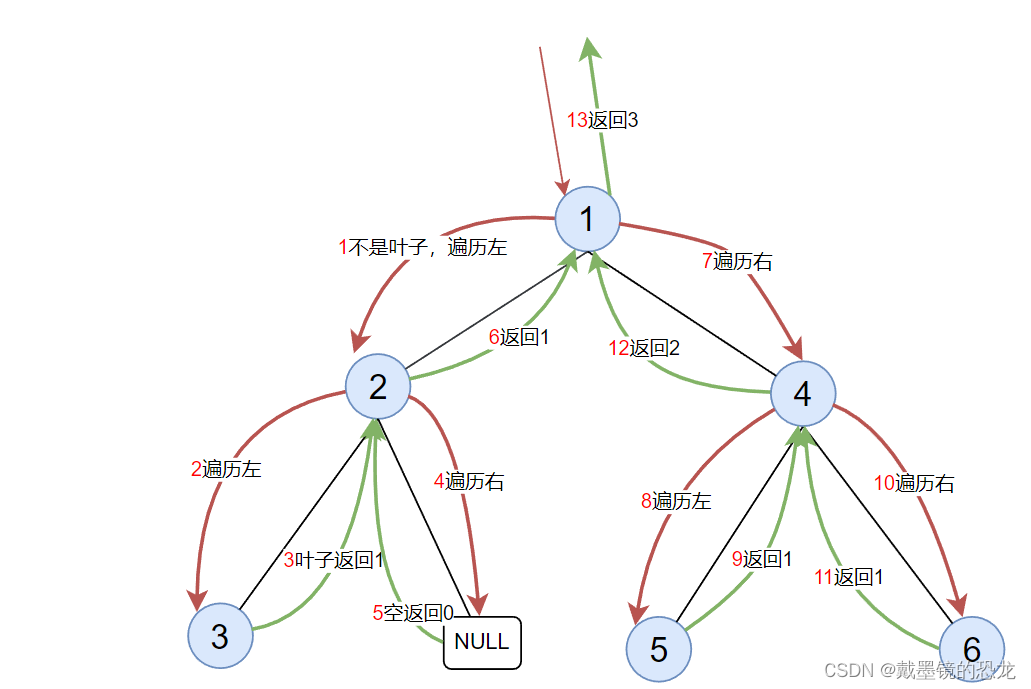
int BinaryTreeLeafSize(TreeNode* root)
{
	//空树，返回空
	if (root == NULL)
	{
		return 0;
	}
	//叶子，返回1
	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}
	//继续遍历左右子树
	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

6.第k层节点的个数

不是第k层就继续遍历左右子树，空树返回0；第k层就返回1。
假设K等于3

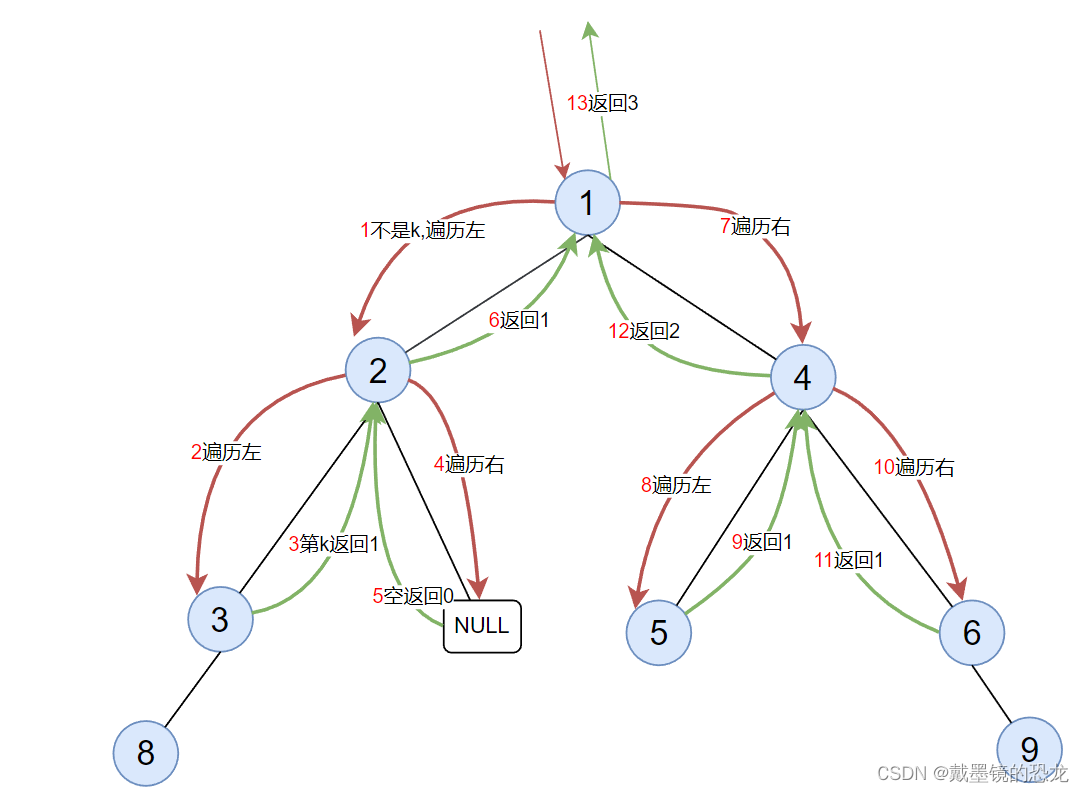
int TreeKLevel(TreeNode* root, int k)
{
	//空树
	if (root == NULL)
	{
		return 0;
	}
	//到第k层
	if (k == 1)
	{
		return 1;
	}
	//未到第k层，继续在左右子树中寻找
	//层数减少
	return TreeKLevel(root->left,k-1) + TreeKLevel(root->right,k-1);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

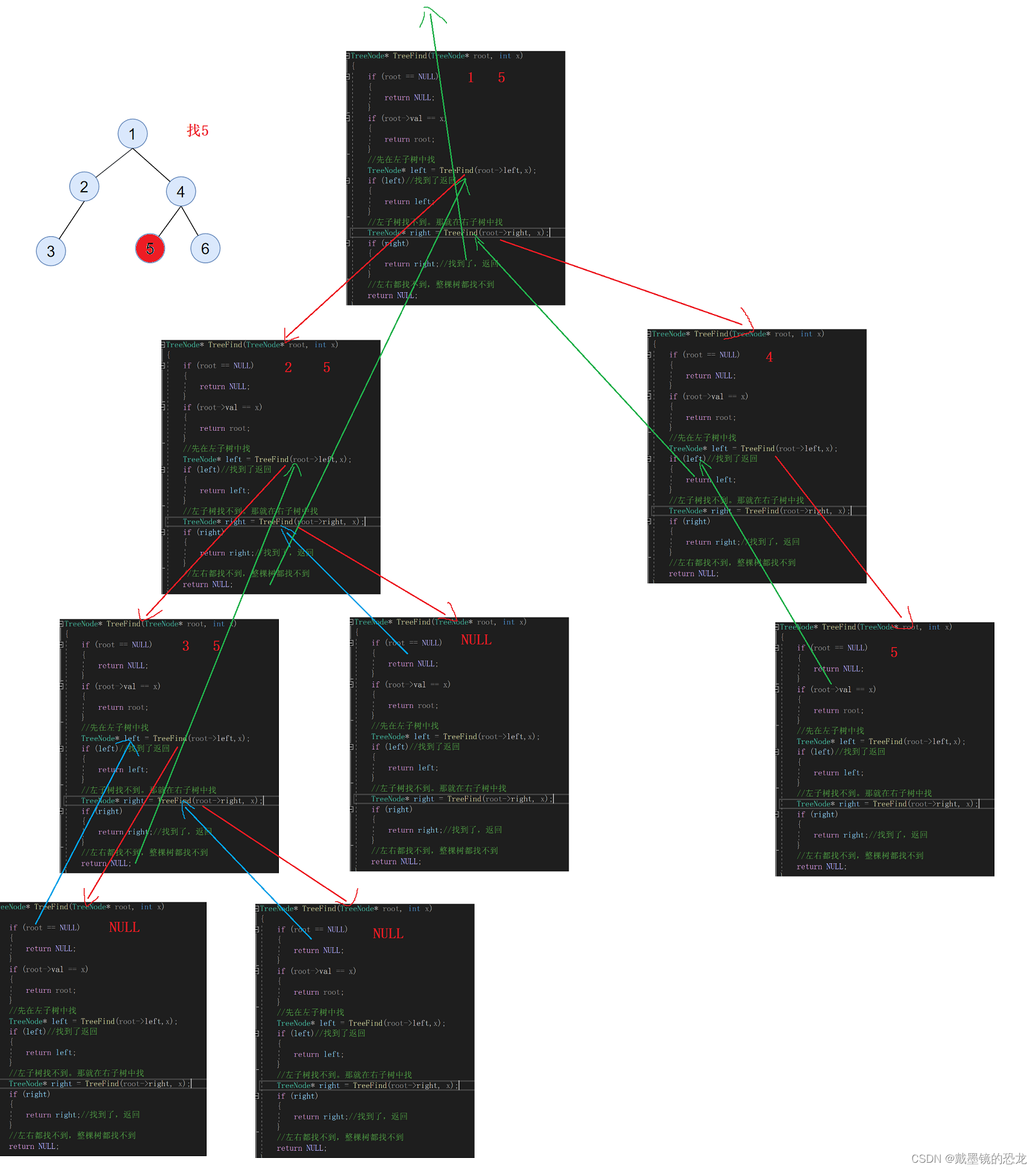
7.查找x所在的节点

当前节点为空数，返回NULL，当前节点是x，返回x的地址；当前节点不是x，先在左子树中找，左子树找不到，再到右子树中找。

TreeNode* TreeFind(TreeNode* root, int x)
{
	if (root == NULL)
	{
		return NULL;
	}
	if (root->val == x)
	{
		return root;
	}
	//先在左子树中找
	TreeNode* left = TreeFind(root->left,x);
	if (left)//找到了返回
	{
		return left;
	}
	//左子树找不到。那就在右子树中找
	TreeNode* right = TreeFind(root->right, x);
	if (right)
	{
		return right;//找到了，返回
	}
	//左右都找不到，整棵树都找不到
	return NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

8.树的销毁

//树的销毁，采用后序遍历销毁
void TreeDestroy(TreeNode* root)
{
	if (root == NULL)
		return;

	TreeDestroy(root->left);
	TreeDestroy(root->right);

	free(root);
}
1
2
3
4
5
6
7
8
9
10
11

9.相关题目

9.1相同的树

题目链接
先比较两树的根是否相等，若相等，在比较子树是都对应相等；若不相等，直接返回false。

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    //两根都为空，相等
    if(p == NULL && q == NULL)
        return true;
    //一个为空、一个不为空，不相等
    if(p == NULL || q == NULL)
        return false;
    //对应节点不相等
    if(p->val != q->val)
        return false;
    //两根相等,检查左、右子树相不相同
    return isSameTree(p->left,q->left) && isSameTree(q->right,p->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13

9.2单值二叉树

题目链接
若当前节点的值不等于根的值，直接false；若当前节点为NULL，则返回true，当前节点不是空，则检查它左树与右数的值等不等于根的值。

bool UnivalTree(struct TreeNode* root ,int val)
{
    if(root == NULL)
    {
        return true;
    }
    if(root->val != val)
    {
        return false;
    }

    return UnivalTree(root->left,val) && UnivalTree(root->right,val);
}

bool isUnivalTree(struct TreeNode* root) {
    if(root == NULL)
    {
        return true;
    }
    int val = root->val;

    return UnivalTree(root,val);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

bool isUnivalTree(struct TreeNode* root) {
    if(root == NULL)
        return true;
    if(root->left && root->left->val != root->val)
        return false;
    if(root->right && root->right->val != root->val)
        return false;
    return isUnivalTree(root->left) 
        && isUnivalTree(root->right);
}
1
2
3
4
5
6
7
8
9
10

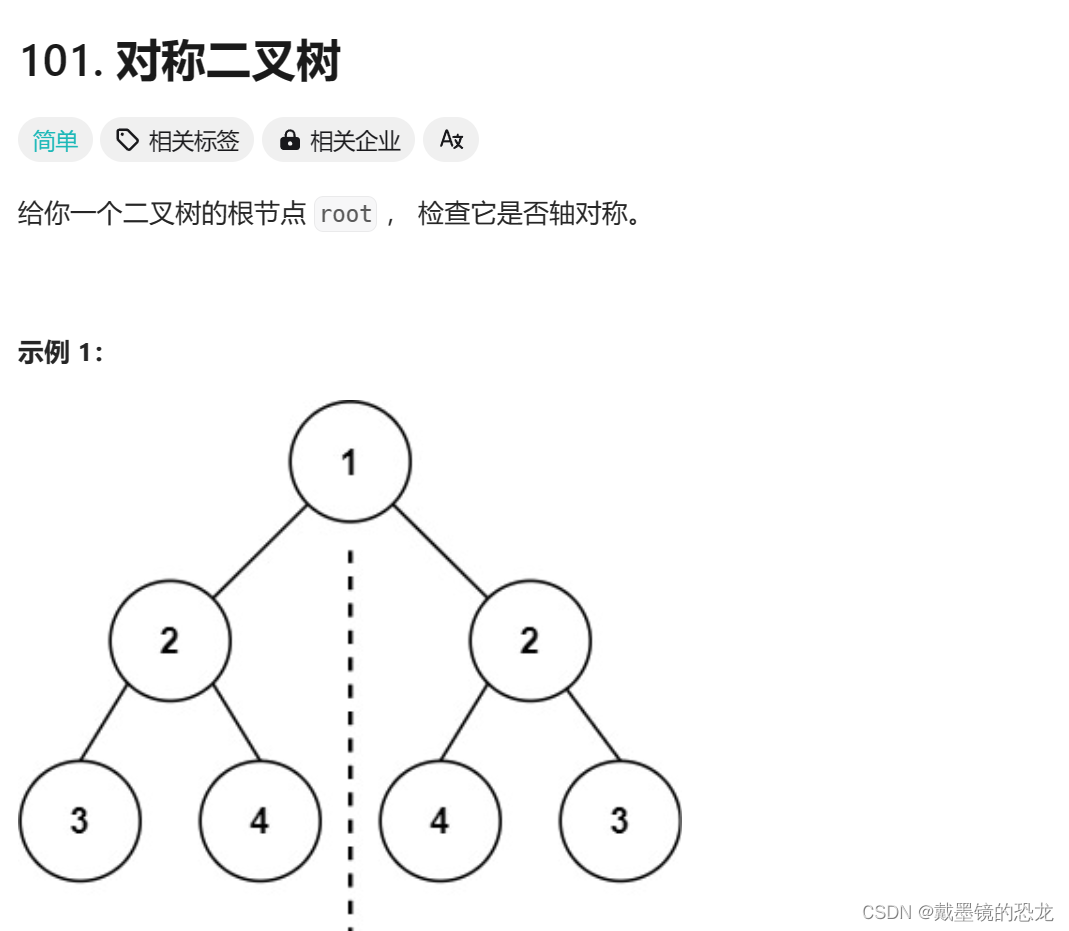
9.3对称二叉树

题目链接

bool check(struct TreeNode* left,struct TreeNode* right)
{
    if(left == NULL && right == NULL)
    {
        return true;
    }

    if(left == NULL || right == NULL)
    {
        return false;
    }
    //当前节点相等，遍历左右子树
    return left->val == right->val
        && check(left->left,right->right)
        && check(left->right,right->left);
}

bool isSymmetric(struct TreeNode* root) {
    if(root == NULL)
    {
        return true;
    }
    return check(root->left,root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

9.4二叉树的构建

题目链接

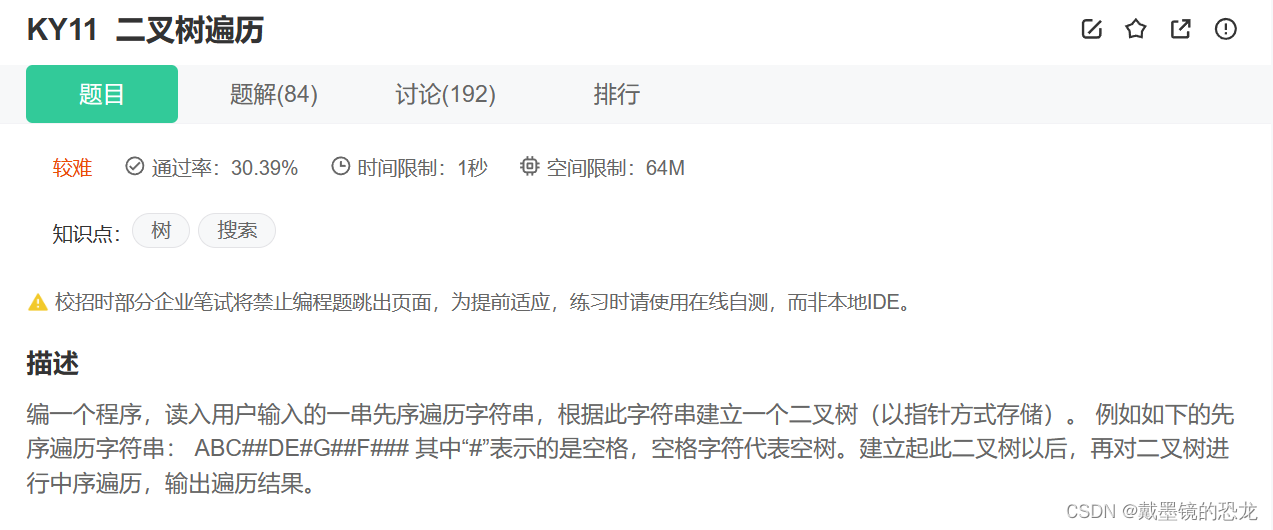
//前序遍历，构建二叉树
TreeNode* CreatTree(char* a, int* pi)
{
	if (a[*pi] == '#')
	{
		(*pi)++;
		return NULL;
	}
	//先构建根
	TreeNode* root = (TreeNode*)malloc(sizeof(TreeNode));
	root->val = a[(*pi)++];
	//然后构建左右子树
	root->left = CreatTree(a, pi);
	root->right = CreatTree(a, pi);
	return root;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

9.5翻转二叉树

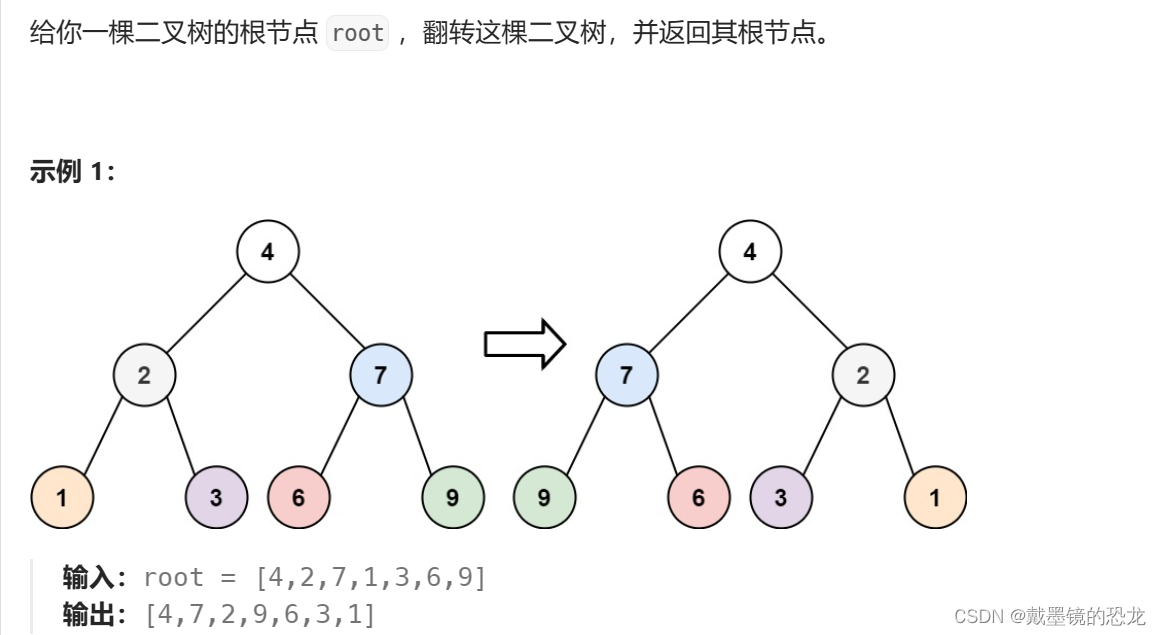
题目链接
思路：将根的子树依次进行交换

struct TreeNode* invertTree(struct TreeNode* root) {
    if(root == NULL)
        return NULL;

    //交换当前树的左右子树
    struct TreeNode* tmp = root->left;
    root->left = root->right;
    root->right = tmp;

    //递归交换左右子树
    invertTree(root->left);
    invertTree(root->right);

    return root;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

9.6另一颗树的子树

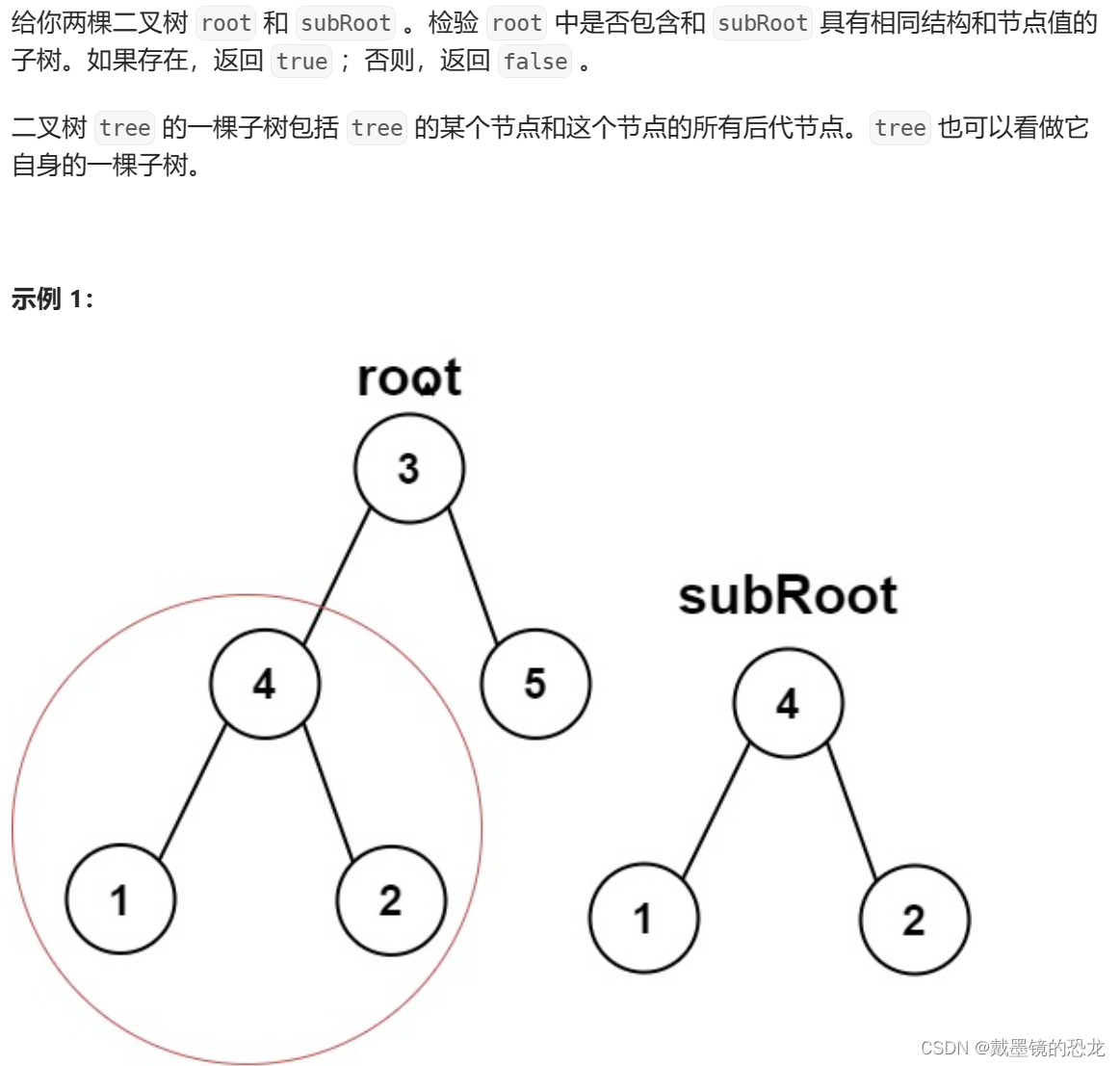
题目链接
其实这一题就是9.1的变种，本质上还是找两棵相同的树。

• 若当前根节点与另一棵树相等，那就从当前节点开始，依次比较子树，检查是否相等。
• 若子树为空或与另一棵树不相等，则返回false.

bool isSameTree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if(root == NULL && subRoot == NULL)
        return true;
    if(root == NULL || subRoot == NULL)
        return false;
    if(root->val != subRoot->val)
        return false;
    return isSameTree(root->left,subRoot->left)
        && isSameTree(root->right,subRoot->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root == NULL)
        return false;//此处是false
    if(root->val == subRoot->val && isSameTree(root,subRoot))
        return true;
    return isSubtree(root->left,subRoot)
        || isSubtree(root->right,subRoot);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

10.判断二叉树是否是完全二叉树

思路：与层序遍历类似，依然使用入队出队的方式。‘
如果当前出队元素为NULL,则队中的剩余元素必须全部为空，否则就不是一棵完全二叉树。

// 判断二叉树是否是完全二叉树
int BinaryTreeComplete(TreeNode* root)
{
	Queue q;
	QueueInit(&q);
	if (root)
	{
		QueuePush(&q, root);
	}
	while (!QueueEmpty(&q))
	{
		TreeNode* front = QueueFront(&q);
		QueuePop(&q);
		//若当前出队元素不是空，则该元素出队，将它的孩子进队
		if (front)
		{
			QueuePush(&q, front->left);
			QueuePush(&q, front->right);
		}
		else
		{
			//当前出的元素是空，停止出
			break;
		}
	}
	//继续出，检查有无非空节点
	while (!QueueEmpty(&q))
	{
		TreeNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front != NULL)
		{
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38