强化学习的学习之路（十七）_2021-01-17:DQN(Deep Q Network：Human-level control through deep reinforcement learning)_behavior network和target network

作为一个新手，写这个强化学习-基础知识专栏是想和大家分享一下自己学习强化学习的学习历程，希望对大家能有所帮助。这个系列后面会不断更新，希望自己在2021年能保证平均每日一更的更新速度，主要是介绍强化学习的基础知识，后面也会更新强化学习的论文阅读专栏。本来是想每一篇多更新一点内容的，后面发现大家上CSDN主要是来提问的，就把很多拆分开来了（而且这样每天任务量也小一点哈哈哈哈偷懒大法）。但是我还是希望知识点能成系统，所以我在目录里面都好按章节系统地写的，而且在github上写成了书籍的形式，如果大家觉得有帮助，希望从头看的话欢迎关注我的github啊，谢谢大家！另外我还会分享深度学习-基础知识专栏以及深度学习-论文阅读专栏，很早以前就和小伙伴们花了很多精力写的，如果有对深度学习感兴趣的小伙伴也欢迎大家关注啊。大家一起互相学习啊！可能会有很多错漏，希望大家批评指正！不要高估一年的努力，也不要低估十年的积累，与君共勉！

---

接下来的几个博客将会分享以下有关DQN算法及其改进，包括DQN（Nature）、Double DQN、 Multi-step DQN、Pirority Replay Buffer、 Dueling DQN、DQN from Demonstrations、Distributional DQN、Noisy DQN、Q-learning with continuous actions、Rainbow、Practical tips for DQN等。

DQN整体对比Q-learning有以下改进：

• 数据预处理

  • Atari 游戏的原生尺寸为210 × 160,每个像素有128 种颜色，将其转换成84 × 84 维度的灰度图。变换后的图像依然保留了主要的信息，同时减轻了数据处理的负担。
  • 虽然Atari 游戏是一个动态的游戏，但是每一时刻Agent 只能从环境中获得1帧信息，而这种静态的图像信息很难表示游戏的动态信息。以乒乓球游戏为例，当画面静止时我们无法判断球要飞向哪一方。为此，算法将收集从当前时刻起的前N帧画面，并将这些信息结合起来作为模型的输入。获得了一定时间内集合的状态信息，模型可以学习到更准确的行动价值，在实验中N 被设置为4 。
  • 不同的Atari 游戏的得分系统不同，有的得分可以上万，有的得分只有几十。为了模型能够更好地拟合长期回报，我们需要
    将得分压缩到模型擅长处理的范围中，我们将每一轮得到的回报压缩到［－ 1, 1］ 。

• 环境交互

  Atari 游戏的可行状态数量非常多，因此如何更好地探索更多的状态变得十分关键。DQN 采用了$ϵ-$ greedy 的策略，一开始策略以100% 的概率随机产生行动，随着训练的不断进行，这个概率将不断衰减，最终衰减至10% 。也就是说，有90% 的概率执行当前最优策略。这样，从以探索为主的策略逐渐转变成以利用为主的策略，两者得到了很好的结合。

• 模型结构

  前面提到价值模型是从 $|S|\times |A|$ 到 $R$ 的映射，采用这种方法构建模型自然是可以的，但是它还有一些缺点。当模型需要通过值函数求解最优策略时，我们需要计算 |A|次才能求出，在实际中这样的计算方法效率较低。为了简化计算，我们可以将模型变成 $S\to {\left[R_i\right]}_{i=1}^{|A|}$ 这样的形式，模型的输出为长度为 $|\mathbf{A}|$ 的向量，向量中的每一个值表示对 应行动的价值估计。这样我们只需要一次计算就可以求出所有行动的价值，无论行动有多少，我们评估价值的时间是一样的。两个模型的表示形式差异如下图：
  

模型的主体采用了卷积神经网络的结构：

1. 第一层卷积层的卷积核为 $8\times 8,$ stride $=4,$ 输出的通道数为 32，此后应用 ReLU非线性层。
2. 第二层卷积层的卷积核为 $4\times 4,$ stride $=2,$ 输出的通道数为 64，此后应用 ReLU 非线性层。
3. 第三层卷积层的卷积核为 $3\times 3,$ stride $=1,$ 输出的通道数为 64，此后应用 ReLU 非线性层。
4. 第四层是全连接层，输出的维度为 512，此后应用 ReLU 非线性层。
5. 最后一层全连接层得到对应行动的价值估计，输出维度与可行的行动数量相关，一 般在 4 ~18 个。

• Random Start
  有些Atari 游戏的起始画面是完全一样的，例如Space Invader ，如果每次我们都从一个固定的场景开始做决策，那么Agent 总要对这些相同的画面进行决策，这显然不利于我们探索更多的画面进行学习。为了增强探索性同时不至于使模型效果变糟，我们可以设定在游戏开始很短的一段时间内，让Agent 执行随机的行动，这样可以最大程度地获得不同的场景样本。

• Frame-Skipping

模拟器可以达到每秒60 帧的显示速率，但是实际上人类玩家无法实现如此高频率的操作，因此我们可以设定每隔一定帧数执行一次行动，例如每隔4帧进行一次行动选择，那么中间的几帧将重复执行前面选择的行动，这样相当于模仿了人类按下某个按钮并持续一段时间的效果。

此外，相邻帧之间的画面存在着极大的相似性，对于十分相似的画面，我们通常可以采用相同的行动，因此这样跳过一定帧数的判断也是合理。

• Replay Buffer

Q-Leaming 方法基于当前策略进行交互和改进，更像是一种在线学习（ Online Learning ）的方法，每一次模型利用交互生成的数据进行学习，学习后的样本被直接丢弃。但如果使用机器学习模型代替表格式模型后再采用这样的在线学习方法，就有可能遇到两个问题。
( 1 ）交互得到的序列存在一定的相关性。交互序列中的状态行动存在着一定的相关性，而对于基于最大似然法的机器学习模型来说，我们有一个很重要的假设：训练样本是独立且来自相同分布的，一旦这个假设不成立，模型的效果就会大打折扣。而上面提到的相关性恰好打破了独立同分布的假设，那么学习得到的值函数模型可能存在很大的波动。
( 2 ）交互数据的使用效率。采用梯度下降法进行模型更新时，模型训练往往需要经过多轮迭代才能收敛。每一次迭代都需要使用一定数量的样本计算梯度， 如果每次计算的样本在计算一次梯度后就被丢弃，那么我们就需要花费更多的时间与环境交互并收集样本。

因此DQN采用了如下图所示的Replay Buffer结构：

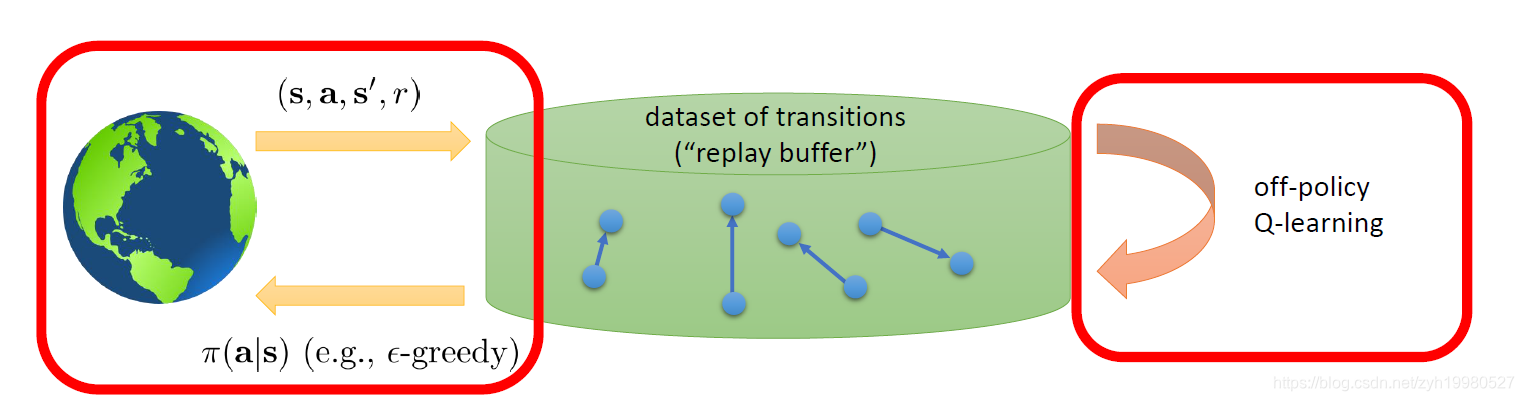
从上图中可以看出，Replay Buffer 保存了交互的样本信息，一般来说每一个样还会保存其他的信息。Replay Buffer 的大小通常会设置得比较大, 例如，将上限设置为可以存储 100 万个样本，这样较长一段时间的样本都可以被保存起来。在训练值函数时，我们就可以从中取出一定数量的样本，根据样本记录的信息进 行训练。

总的来说，Replay Buffer 包含了收集样本和采样样本两个过程。收集的样本按照时间先后顺序存人结构中，如果 Replay Buffer 已经存满样本，那么新的样本会将时间上最久远的样本覆盖。而对采样来说，如果每次都取出最新的样本，那么算法就和在线学习相差不多; 一般来说，Replay Buffer 会从缓存中均匀地随机采样一批样本进行学习。

均匀采样的好处是什么呢？采用均匀采样后，每次训练的样本通常来自多次交互序列，这样单一序列的波动就被减轻很多，训练效果也就稳定了很多。同时，一份样本也可以被多次训练，提高了样本的利用率。

• Target Network

  模型不稳定的另外一个原因来自算法本身。从 Q-Learning 的计算公式可以看出, 算法可以分成如下两个步骤。
  （1 ）计算当前状态行动下的价值目标值:

  $\Delta q(s,a)=r\left(s^{\prime }\right)+{\max }_{a^{\prime }}{q}^{T-1}{\left(s^{\prime },a^{\prime }\right)}_{})$

  （2）网络模型的更新：

  $q^T(s,a)=q^{T-1}(s,a)+\frac{1}{N}{\left[\Delta q(s,\mathbf{a})-q^{T-1}(s,a)\right]}_{}$

  可以看出模型通过当前时刻的回报和下一时刻的价值估计进行更新，这就像一场猫捉老鼠的游戏，猫在快速移动，老鼠也在快速移动，最终得到的轨迹自然是杂乱无章不稳定的。
  
  
  这里存在一些隐患，前面提到数据样本差异可能造成一定的波动，由于数据本身存在着不稳定性，每一轮迭代都可能产生一些波动，如果按照上面的计算公式，这些波动会立刻反映到下一个迭代的计算中，这样我们就很难得到一个平稳的模型。为了减轻相关问题带来的影响，我们需要尽可能地将两个部分解耦。

  为此论文作者引人了目标网络（Target Network ），它能缓解上面提到的波动性问题。这个方法引人了另一个结构完全一样的模型，这个模型被称为 Target Network，而原本的模型被称为表现模型（Behavior Network ）。两个模型的训练过程如下所示。
  （1）在训练开始时，两个模型使用完全相同的参数。
  （2）在训练过程中，Behavior Network 负责与环境交互，得到交互样本。
  （3）在学习过程中，由 Q-Learning 得到的目标价值由 Target Network 计算得到; 然 后用它和 Behavior Network 的估计值进行比较得出目标值并更新 Behavior Network。
  （4）每当训练完成一定轮数的迭代，Behavior Network 模型的参数就会同步给 Target Network，这样就可以进行下一个阶段的学习了。

  通过使用 Target Network，计算目标价值的模型在一段时间内将被固定，这样模型 可以减轻模型的波动性。
  以上就是 DQN 模型的主要内容，完整的算法流程如下所示:
  

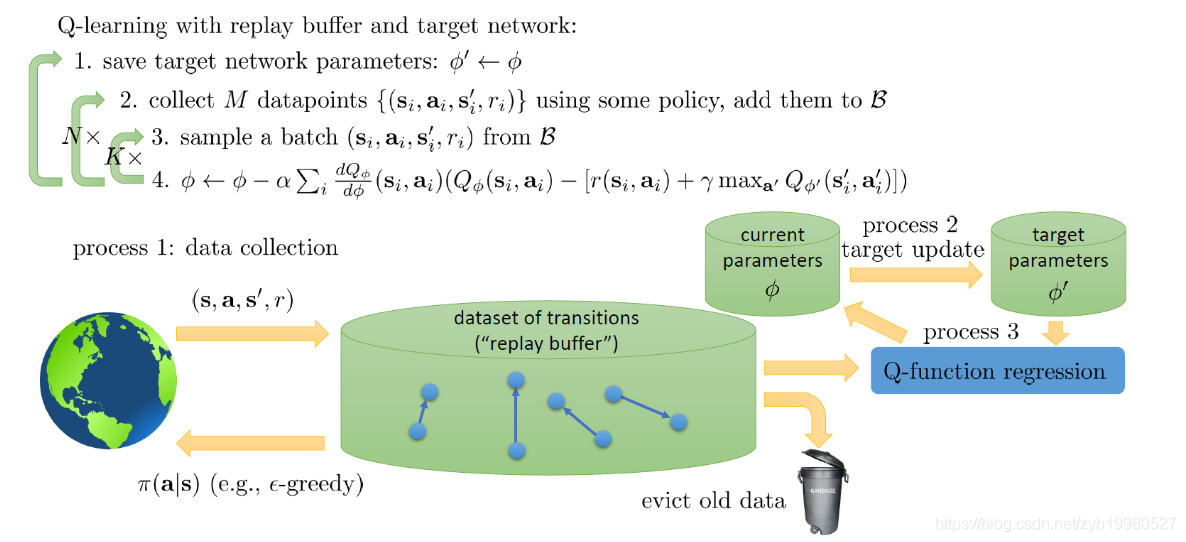
上一篇：强化学习的学习之路（十六）_2021-01-16:价值函数近似（Value function approximation）

下一篇：强化学习的学习之路（十八）_2021-01-18：Double Q-learning（Deep Reinforcement Learning with Double Q-learning）