推荐系统（4）——推荐算法1(基于内容和协同过滤)_基于内容的协同过滤算法

推荐算法在机器学习之前就有很广泛的应用合需求了，当前也发展了很多种类的算法，但是应用最广的依然是协同过滤算法流派的。

概括来说，主要分为五种推荐算法：

1 基于内容的推荐（Content Based）

CB应该是最早使用的推荐系统算法了，最早使用在信息检索系统里面，所以很多信息检索及信息过滤里的方法都能用于CB中。 比如TF-IDF计算。

1.1 原理

基于用户A的感兴趣物品B，来推荐类似B的B1，B2等等物品。

比如你喜欢看《变形金刚1》，系统就可能给你推荐该系列的2，3，4等。

因此基于内容的推荐，提取推荐对象的特征 ，是内容推荐算法的关键。但是对于多媒体内容，很难找到物品之间的特性关联。

1.2 算法流程

参考自：http://www.cnblogs.com/breezedeus/archive/2012/04/10/2440488.html
CB的过程一般包括以下三步：

1. Item Representation：为每个item抽取出一些特征（也就是item的content了）来表示此item；

2. Profile Learning：利用一个用户过去喜欢（及不喜欢）的item的特征数据，来学习出此用户的喜好特征（profile）；

3. Recommendation Generation：通过比较上一步得到的用户profile与候选item的特征，为此用户推荐一组相关性最大的item。

对于上面的三个步骤给出一张很细致的流程图（第一步对应着Content Analyzer，第二步对应着Profile Learner，第三步对应着Filtering Component）：

第一步：特征提取

对于一个item，比如一篇文章，我们采用这篇文章的词来代表这篇文章，（类似摘要）。通过TF-IDF（词频-逆文档频率）来计算每个词的权重，实现item——>特征向量。

第二步：建立用户喜好模型

根据用户的喜好，通过机器学习模型进行二分类，来预测新的item用户是否会喜欢。常用的模型就是统计机器学习，比如LR，DT，SVM，KNN等等。

第三步：推荐迭代

根据模型的预测结果，生成一个推荐列表。

1.3 优/缺点

优点

• 简单有效，容易理解，不需要领域知识
• 不需要用户的历史数据
• 不存在新item的冷启动问题（因为是基于特征的推荐），对比cf有明显优势。
• 不存在稀疏问题

缺点

• 受item特征提取的制约

在很多情况下，item的特征提取很难，对于文档我们可以较为容易看的提取关键词，但是对于多媒体数据，比如电影推荐的item电影，社会化网络推荐的item人，这些item都不容易提取。

其实，几乎在所有实际情况中我们抽取的item特征都仅能代表item的一些方面，不可能代表item的所有方面。这样带来的一个问题就是可能从两个item抽取出来的特征完全相同，这种情况下CB就完全无法区分这两个item了。比如如果只能从电影里抽取出演员、导演，那么两部有相同演员和导演的电影对于CB来说就完全不可区分了

• 基于用户喜好的推荐，新颖度不够，不会出现新的item的推荐
• 存在新User的冷启动问题（没有偏好标签，无法有效推荐）
• 需要数据量大，满足机器学习模型

2 协同过滤（Collaborative Filtering）

2.1 CF的理论基础

协同过滤算法作为推荐系统的最经典算法，至今在工业界依然被广泛应用。主要分为2种，分别是基于领域的协同过滤算法和基于模型的协同过滤算法。前者主要是根据计算相似性来进行推荐，后者根据历史数据建立一个模型，在基于模型进行推荐预测。主要的模型是：NN，LFM（潜在语义分析），贝叶斯网络聚类模型等。

在推荐系统中，“关系”主要是通过关系矩阵存储，主要归纳为用户-用户（U-U）矩阵，用户-物品矩阵(U-V)和物品-物品(V-V)矩阵。基于领域的CF主要是基于相似度形成推荐结果。下面介绍相似度计算基础。

（1）U-U矩阵相似度计算（Pearson系数）

计算矩阵相似度的方法有多种，Pearson系数，余弦相似度，修正的余弦相似度，Spearman秩相关系数和均方差等。有关研究发现计算用户矩阵相似度任务上，Pearson系数的表现优于其他计算方法。

Pearson原理:
计算流程：

Pearson存在的问题：

• 用户之间具有较少共同item时评价不准
• 无法解释不同用户对热门item高分带来高相似度的想象

解决方法：

提高对有争议的共同评价的相对重要性，降低了广受欢迎项目有共同评价的相对重要性

（2）V-V矩阵相似度计算（余弦相似度）

余弦相似度用来计算物品之间的相似度具有明显的优势

1.算法原理

余弦相似度通过夹角的距离来判断两个变量之间的距离。

$$sim(x,y)=cos(x,y)=\frac{x\cdot y}{|x{|}_2\times |y{|}_2}$$

修正后的余弦相似度就是对变量进行中心化，从数学角度上，等价于皮尔森相关系数。

2.算法步骤

（3）U-V矩阵降维

2.2 基于领域的协调过滤推荐

在这里领域指的就是用户和物品的关联关系，汇总所有<user,item>的用户行为, 利用集体智慧做推荐。主要分为基于用户的协同过滤（User-CF）和基于物品的协调过滤（Item-CF）。

• User-CF：通过对用户喜欢的item进行分析, 发现用户A和用户B很像(他们都喜欢差不多的东西), 用户B喜欢了某个item, 而用户A没有发现, 那么就把这个item推荐给用户A。

• Item-CF：发现itemA和itemB很像(他们被差不多的人喜欢), 那么就把用户A喜欢的所有item, 将这些item类似的item列表拉出来, 作为被推荐候选推荐给用户A。

如上说的都是个性化推荐, 如果是相关推荐, 就直接拿Item-Based CF的中间结果就好啦。

主要是通过U-V矩阵来构建：

（1）User-CF

给用户推荐和他兴趣相似的其他用户喜欢的物品。

1.算法原理

• step1：找到和目标用户兴趣相似的用户群体
  收集用户和item的历史信息，计算用户和其他用户之间的相似度Sim(u,Ni)，找到和目标用户相似的用户群体N（u）。
• step2：找到这个群体中目标用户喜欢的，但是没有接触过的物品，进行推荐。
  基于用户的协同过滤子引擎，通过下面公式来实现用户对item的喜欢程度预测
  计算图解如下：

2.算法流程
U-U矩阵的输出就是Use-CF的输入矩阵。

3.算法举例

4.优缺点
适用于用户较少，个性化不明显的相似人群的推荐。

优点：

• 实现简单
• 可以推荐出新颖的item
• 新产品一旦有用户产生行为，就可以立刻被推荐给其他用户

缺点：

• 随着用户增多，数据稀疏性问题严重，适用于用户少的系统
• 可解释性差
• 实时更新较差

（2）Item-CF

1.算法原理

2.算法流程

3.算法步骤

4 算法举例

5.优缺点

适用于用户较多，物品远小于用户，个性化突出的情况。

优点

• 长尾物品丰富，更满足个性化推荐
• 用户的新行为一定导致推荐系统立马更新
• 可解释性强
• 新用户一旦产生行为，就可以立马给他推荐相关产品。

缺点：

• 新产品难以推荐给用户，因为物品相似度矩阵没有更新。

（3）两种模式的比较

协同过滤的优点：

• 实现快
• 效果不错

CF缺点：

• 冷启动问题
• 马太效应（强者愈强）
• 推荐解析模糊

参考：https://blog.csdn.net/duyibo123/article/details/110915485

2.3 基于模型的协同过滤推荐

基于模型的推荐算法，是与基于近邻的推荐算法相对的。基于近邻的推荐算法，主要是将所有的用户数据，读入内存，进行运算，当数据量特别大时，显然这种方法是不靠谱的。因此出现了基于模型的推荐算法，依托于一些机器学习的模型，通过离线进行训练，在线进行推荐。

基于模型推荐系统的优势：

• 节省空间:一般情况下，学习得到的模型大小远小于原始的评分矩阵，所以空间需求通常较低。
• 训练和预测速度快:基于近邻的方法的一个问题在于预处理环节需要用户数或物品数的平方级别时间，而基于模型的系统在建立训练模型的预处理环节需要的时间往往要少得多。在大多数情况下，压缩和总结模型可以被用来加快预测

基于模型的研究就多了, 常见的有:

• 基于潜语义分析
• 基于矩阵分解
• 基于贝叶斯网络
• 基于SVM

（1）隐语义模型（latent factor model，LFM）

1. LFM简介

隐语义模型的核心时通过隐含特征联系用户兴趣的物品.

现从简单例子出发介绍隐语义模型的基本思想。假设用户A喜欢《数据挖掘导论》，用户B喜欢《三个火枪手》，现在小编要对用户A和用户B推荐其他书籍。

基于 UserCF(基于用户的协同过滤)，找到与他们偏好相似的用户，将相似用户偏好的书籍推荐给他们；

基于ItemCF(基于物品的协同过滤)，找到与他们 当前偏好书籍相似的其他书籍，推荐给他们。

其实还有一种思路，就是根据用户的当前偏好信息，得到用户的兴趣偏好，将该类兴趣对应的物品推荐给当前用户。比 如，用户A喜欢的《数据挖掘导论》属于计算机类的书籍，那我们可以将其他的计算机类书籍推荐给用户A；用户B喜欢的是文学类数据，可将《巴黎圣母院》等这 类文字作品推荐给用户B。

这就是隐语义分析，依据“兴趣”这一隐含特征将用户与物品进行连接，需要说明的是此处的“兴趣”其实是对物品类型的一个分类而已。对于一个用户首先得到他的兴趣分类，然后从分类中挑选出他可能喜欢的物品。基于兴趣分类，需要解决以下问题：

1. 如何给物品分类
2. 如何确定用户的兴趣分类，以及权重
3. 给定分类后，如何选择这个类的那些物品推荐，确定物品在分类的权重

人工编辑分类的问题：

1. 编辑具有主观性
2. 编辑难以控制分类粒度
3. 编辑难以给物品多个分类
4. 编辑难以给出多维度分类
5. 编辑很难决定物品在某一个分类的权重

隐语义分析解决了以上问题：

1. 用户的行为代表了用户对物品分类的看法。比如，如果两个物品被很多用户同时喜欢，这个两个物品很可能属于同一类。
2. 隐语义技术允许我们指定最终的分类数目，分类数越多，分类粒度越细。
3. 隐语义技术可以计算出物品属于每个类的权重，因为每个物品不是硬性地被分到一个类目中。
4. 隐语义技术给出的每个分类都不是一个维度，它根据用户的共同兴趣计算得出。
5. 隐语义技术可以通过统计用户行为决定物品在每个类中的权重，如果喜欢某个类的用户都会喜欢某个物品，那么这个物品在这个类中的权重就可能较高。

隐语义技术有很多著名的模型和方法，其中耳熟能详的名词有pLSA、LDA、隐含类别模型、隐含主题模型、矩阵分解。这些技术和方法在本质上是相同的，都可以用于个性化推荐系统。

2.数学推导

其中，$u_i$代表用户，$k_i$代表定义的隐分类个数，$I_j$代表物品，$p_{1,k}$代表用户$u_1$对k隐类的关系，$q_{1,k}$代表物品$I_1$与第$k$隐类的权重系数，系数越大说明$I_1$与k类的关系程度越高。推出用户$u_i$对于物品$I_j$的兴趣计算公式为：

$$preference(u,i)=r_{ui}=p_u^T{q}_i=\sum _{f=1}^F{p}_{u,k}{q}_{i,k}$$

3.正负样本构建

我们知道推荐系统中用户的行为分为显性反馈和隐性反馈，LFM在显性反馈（评分数据）上解决评分预测可以有很好的精度，但是对于隐性反馈（没有不喜欢什么的数据），在隐性反馈中需要为用户生成负样本，Rong Pan 在其文章中对负样本的生成做了讨论：

1. 对于一个用户，他没有过行为的物品作为负样本
2. 从他没有行为的物品均匀采样出一些物品作为负样本
3. 从没有行为的物品中采样，但是采样时保证用户的正负样本数目相当
4. 从没有行为的物品中采样，偏重不热门的物品。

Rong Pan 在论文中提出1负样本太多，计算复杂度高且精度差，3好于2，2好于4。 后来在11年的KDD Cup 推荐系统比赛中，发现应该遵循如下原则：

1. 每个用户保证正负样本的均衡
2. 采样负样本时选取很热门但是用户没有行为的物品

4.模型求解

上述LFM算法的网络构造思路非常类似于神经网络，所以对于该算法的求解思路可以分为两种：

1. 可以用最大似然函数来求解，这种算法是从概率学的角度求解。

2. 将这种算法转化为求解损失函数极小值的方式，通过梯度下降法来求解模型系数。

定义损失函数：

$$C=\sum _{(u,i)\in K}{(r_{ui}-{\hat{r}}_{ui})}^2=\sum _{(u,i)\in K}{(r_{ui}-\sum _{k=1}^K{p}_{u,k}{q}_{i,k})}^2+\lambda ||p_u|{|}^2+\lambda ||q_i|{|}^2$$

其中${\tilde{r}}_{i,j}$为预测的兴趣度，$r_{i,j}$为用户实际对商品兴趣度，正样本r=1，负样本r=-1，损失函数loss就是他们的误差平方和。${\Vert p_i\Vert }^2$和${\Vert q_j\Vert }^2$为惩罚系数，其作用就是为了防止过拟合，因为当K足够大时总能找到一组参数使得loss达到最小，但是很容易过拟合，$\lambda$参数可以用来控制拟合程度，值越大惩罚越重越不容易发生过拟合。

随机梯度下降（SVG）：
∂ C ∂ P U k = − 2 ( R U I − ∑ k = 1 K P U , k Q k , I ) Q k I + 2 λ P U k ∂ C ∂ Q k I = − 2 ( R U I − ∑ k = 1 K P U , k Q k , I ) P U k + 2 λ Q k I

$$\begin{array}{l} \frac{\partial \mathrm{C}}{\partial P_{U k}}=-2\left(R_{U I}-\sum_{k=1}^{K} P_{U, k} Q_{k, I}\right) Q_{k I}+2 \lambda P_{U k} \\ \frac{\partial \mathrm{C}}{\partial Q_{k I}}=-2\left(R_{U I}-\sum_{k=1}^{K} P_{U, k} Q_{k, I}\right) P_{U k}+2 \lambda Q_{k I} \end{array}$$ ∂PUk​∂C​=−2(RUI​−∑k=1K​PU,k​Qk,I​)QkI​+2λPUk​∂QkI​∂C​=−2(RUI​−∑k=1K​PU,k​Qk,I​)PUk​+2λQkI​​

P U k = P U k + α ( ( R U I − ∑ k = 1 K P U , k Q k , I ) Q k l − λ P U k ) Q k l = Q k l + α ( ( R U I − ∑ k = 1 K P U , k Q k , I ) P U k − λ Q k l )

$$\begin{array}{l} P_{U k}=P_{U k}+\alpha\left(\left(R_{U I}-\sum_{k=1}^{K} P_{U, k} Q_{k, I}\right) Q_{k l}-\lambda P_{U k}\right) \\ Q_{k l}=Q_{k l}+\alpha\left(\left(R_{U I}-\sum_{k=1}^{K} P_{U, k} Q_{k, I}\right) P_{U k}-\lambda Q_{k l}\right) \end{array}$$ PUk​=PUk​+α((RUI​−∑k=1K​PU,k​Qk,I​)Qkl​−λPUk​)Qkl​=Qkl​+α((RUI​−∑k=1K​PU,k​Qk,I​)PUk​−λQkl​)​

参数：

• 隐分类个数K
• 学习速率aphla
• 损失函数的惩罚因子lambda
• 正负样本数比例（实验表明，ratio参数对LFM的性能影响最大。）

1，3，4这三项需要根据推荐系统的准确率、召回率、覆盖率及流行度作为参考, 步长α要参考模型的训练效率。

5.实例说明

雅虎以CTR（点击通过率）作为优化的目标，利用LFM预测用户是否会点击一个连接。但是LFM难以实现实时的推荐，经典的LFM每次扫描所有的用户，计算隐向量 pu, 耗时，冷启动问题非常明显，雅虎的技术人员提出了一个解决方案，利用新闻链接的内容属性（关键词，类别等）得到链接i的内容特征向量 yi， 实时收集用户对链接的行为，利用这些数据得到链接i的隐特征 qi，利用如下公式判断用户u是否会点击链接i
$$r_{ui}=x_u^T.y_i+p_u^T.q_i$$

yi是根据链接内容直接生成， xu是根据历史记录获得的，每天计算一次即可。 pu、qi是利用用户近几个小时的行为训练LFM获得的。

6.优缺点比较

• 很难实现实时推荐
  • 经典的隐语义模型每次训练时都需要扫描所有的用户行为记录，这样才能计算出用户对于 每个隐分类的喜爱程度矩阵P和每个物品与每个隐分类的匹配程度矩阵Q。
  • 隐语义模型的训练需要在用户行为记录上反复迭代才能获得比较好的性能，因此 LFM的每次训练都很耗时，一般在实际应用中只能每天训练一次，并且计算出所有用户的推荐结果。从而隐语义模型不能因为用户行为的变化实时地调整推荐结果来满足用户最近的行为。

7.基于领域的CF和LFM比较

（2）基于LFM——SVD的推荐

1.矩阵分解基本思想

在数学角度上，矩阵分解就是将一个高维矩阵分解成两个低维矩阵的乘积。

在实际推荐计算时不再使用大矩阵，而是使用分解得到的两个小矩阵。按照矩阵分解的原理，我们会发现原来m x n的大矩阵会分解成$U_{m\ast k}$ 和$P_{k\ast n}$的两个小矩阵，这里多出来一个k维向量，就是隐因子向量（Latent Factor Vector）。矩阵分解是隐语义分析模型的一种。

矩阵分解模型假设

通过隐变量来表示用户和物品，他们的乘积构成了原始元素，即用户-物品评分矩阵
1

假设成立的原因在于，因为我们认为实际的交互数据是由一系列的隐变量的影响下产生的，这些隐变量代表了用户和物品一部分共有的特征，在物品身上表现为属性特征，在用户身上表现为偏好特征，只不过这些因子并不具有实际意义，也不一定具有非常好的可解释性，每一个维度也没有确定的标签名字，所以才会叫做“隐变量”。

而矩阵分解后得到的两个包含隐变量的小矩阵，一个代表用户的隐含特征，一个代表物品的隐含特征，矩阵的元素值代表着相应用户或物品对各项隐因子的符合程度，有正面的也有负面的

矩阵分解举例

使用之前的用户一电影评分表，5个用户（U表示），6个电影（M表示）。现在假设电影的风格有以下几类:喜剧，动作，恐怖。分别用K1、K2、K3来表示。那么我们希望得到用户对于风格偏好的矩阵U，以及每个风格在电影中所占比重的矩阵M

通常情况下，隐因子数量k的选取要远远低于用户和电影的数量，大矩阵分解成两个小矩阵实际上是用户和电影在k维隐因子空间上的映射，这个方法其实是也是一种“降维”（Dimension Reduction）过程。

矩阵分解目标：

我们再从机器学习的角度来了解矩阵分解，我们已经知道评分预测实际上是一个矩阵补全的过程，在矩阵分解的时候原来的大矩阵必然是稀疏的，即有一部分有评分，有一部分是没有评过分的，不然也就没必要预测和推荐了。

所以整个预测模型的最终目的是得到两个小矩阵，通过这两个小矩阵的乘积来补全大矩阵中没有评分的位置。所以对于机器学习模型来说，问题转化成了如何获得两个最优的小矩阵。因为大矩阵有一部分是有评分的，那么只要保证大矩阵有评分的位置（实际值）与两个小矩阵相乘得到的相应位置的评分（预测值）之间的误差最小即可，其实就是一个均方误差损失，这便是模型的目标函数。

矩阵分解的优势：

• 比较容易编程实现，随机梯度下降方法依次迭代即可训练出模型。比较低的时间和空间复杂度，高维矩阵映射为两个低维矩阵节省了存储空间，训练过程比较费时，但是可以离线完成；评分预测一般在线计算，直接使用离线训练得到的参数，可以实时推荐。
• 预测的精度比较高，预测准确率要高于基于领域的协同过滤以及内容过滤等方法。

矩阵分解的缺点：

• 模型训练比较费时。
• 推荐结果不具有很好的可解释性，分解出来的用户和物品矩阵的每个维度无法和现实生活中的概念来解释，无法用现实概念给每个维度命名，只能理解为潜在语义空间。

矩阵分解的作用：

• 矩阵填充（通过矩阵分解来填充原有矩阵，例如协同过滤的ALS算法就是填充原有矩阵）
• 清理异常值与离群点
• 降维、压缩
• 个性化推荐
• 间接的特征组合（计算特征间相似度

2.奇异值分解（SVD）

SVD是矩阵分解的其中一种，数学推导在这里 SVD数学推导

对于用户u的隐变量表示$P_u$（用户的兴趣表达向量）和物品的隐变量表示$q_i^T$（物品的特征表达向量）,得到用户u对物品i的评分：

$${\hat{r}}_{ui}=p_u{q}_i^T$$

定义损失函数为：

$$\underset{q^{\ast },p^{\ast }}{\min }\sum _{(u,i)\in \kappa }{\left(r_{ui}-p_u{q}_i^T\right)}^2+\lambda \left({\Vert q_i\Vert }^2+{\Vert p_u\Vert }^2\right)$$

其中，$r_{ui}$是真实评分数据

学习过程：

1. 准备好用户物品的评分矩阵，每一条评分数据看做一条训练样本；
2. 给分解后的U矩阵和V矩阵随机初始化元素值；
3. 用U和V计算预测后的分数；
4. 计算预测的分数和实际的分数误差；
5. 按照梯度下降的方向更新U和V中的元素值；
6. 重复步骤3到5，直到达到停止条件

优化函数

这里不采用我们最常使用的SGD，而是交叉最小二乘（ALS），原因在于：

• 在交替的其中一步，也就是假设已知其中一个矩阵求解另一个时，要优化的参数是很容易并行化的；
• 在不那么稀疏的数据集合上，交替最小二乘通常比随机梯度下降要更快地得到结果

通过优化，使得降维后矩阵乘积尽可能逼近原矩阵。
$$R_{m\times n}=P_{m\times k}\times Q_{n\times k}^T$$

优化过程：（有一点类似EM算法）

1. 初始化随机矩阵Q里面的元素值；
2. 把Q矩阵当做已知的，直接用线性代数的方法求得矩阵P；
3. 得到了矩阵P后，把P当做已知的，故技重施，回去求解矩阵Q；
4. 上面两个过程交替进行，一直到误差可以接受为止。

（3）Bias-SVD

上面的LFM预测公式通过隐类将用户和物品联系在了一起。但是，实际情况下，一个评分系统有些固有属性和用户、物品无关，而用户也有些属性和物品无关，物品也有些属性和用户无关。

例如某些用户非常挑剔，总是给予很低的评分；或是某部电影拍得奇烂，恶评如潮因此， Netflix Prize中提出了另一种LFM，其预测公式如下：
$${\hat{r}}_{ui}=\mu +b_u+b_i+p_u\ast q_i^T$$

通过增加3个训练参数，将SVD模型改进为Bias-SVD模型。参数解释如下：

• $\mu$: 训练集中所有记录的评分的全局平均数。它可以表示网站评分对用户和物品的影响。
• $b_u$: 用户偏置项。用户的$u$的平均评分相对于全局评分$\mu$的偏移，这一项表示了用户的评分习惯中和物品没有关系的那种因素。
• $b_i$: 物品偏置项。物品$i$评分和全局评分$\mu$的偏移，这一项表示了物品接受的评分中和用户没有什么关系的因素。

模型参数bi,bu,qi,pu，通过最优化下面这个目标函数获得：
$$\underset{b_i,b_{u,},q_i,p_u}{\min }\sum _{(u,i)\in K}{\left(r_{ui}-\mu -b_u-b_i-p_u{q}_i^{\top }\right)}^2+\lambda \left\{\sum _u\left(b_u^2+{\Vert p_u\Vert }^2\right)+\sum _i\left(b_i^2+{\Vert q_i\Vert }^2\right)\right\}$$

通过随机梯度下降或者交替最小二乘（ALS）进行参数求解：

b u ← b u + α ( r u i − r ^ u i − λ b u ) b i ← b i + α ( r u i − r ^ u i − λ b i ) q i ← q i + α ( ( r u i − r ^ u i ) p u − λ q i ) p u ← p u + α ( ( r u i − r ^ u i ) q i − λ p u )

$$\begin{aligned} &b_{u} \leftarrow b_{u}+\alpha\left(r_{u i}-\hat{r}_{u i}-\lambda b_{u}\right) \\ &b_{i} \leftarrow b_{i}+\alpha\left(r_{u i}-\hat{r}_{u i}-\lambda b_{i}\right) \\ &q_{i} \leftarrow q_{i}+\alpha\left(\left(r_{u i}-\hat{r}_{u i}\right) p_{u}-\lambda q_{i}\right) \\ &p_{u} \leftarrow p_{u}+\alpha\left(\left(r_{u i}-\hat{r}_{u i}\right) q_{i}-\lambda p_{u}\right) \end{aligned}$$ ​bu​←bu​+α(rui​−r^ui​−λbu​)bi​←bi​+α(rui​−r^ui​−λbi​)qi​←qi​+α((rui​−r^ui​)pu​−λqi​)pu​←pu​+α((rui​−r^ui​)qi​−λpu​)​

（4）SVD++

某个用户对某个电影进行了评分，那么说明他看过这部电影，那么这样的历史行为事实上蕴含了一定的信息，因此我们可以这样来理解问题：评分的行为从侧面反映了用户的喜好

前面的SVD和Bias-SVD都没有显式的考虑用户的过去评分行为对用户评分预测的影响。为此，Koren 在Netflix Prize比赛中提出了一个模型，将用户历史评分的物品加入到了LFM模型中，Koren将该模型称为SVD++。
$${\hat{r}}_{ui}=\mu +b_i+b_u+q_i^{\top }\left(p_u+{\left|I_u\right|}^{-\frac{1}{2}}\sum _{j\in I_u}{y}_j\right)$$

考虑将item-cf的邻域知识加入bias-SVD里面，首先改写下Item-CF的预测公式如下：

$${\hat{r}}_{ui}=\frac{1}{\sqrt{|N(u)|}}\sum _{j\in N(u)}{w}_{ij}$$

这里,$w_{ij}$不再是根据ItemCF算法计算出的物品相似度矩阵，而是一个和P、Q一样的参数，它可以通过优化如下的损失函数进行优化：

$$C(w)=\sum _{(u,i)\in Train}{\left(r_{ui}-\sum _{j\in N(u)}{w}_{ij}{r}_{uj}\right)}^2+\lambda w_{ij}^2$$

从上式可以看到，这个模型有一个缺点，就是w将是一个比较稠密的矩阵，存储它需要比较大的空间。此外，如果有n个物品，那么该模型的参数个数就是n2个，这个参数个数比较大，容易造成结果 的过拟合。因此，Koren提出应该对w矩阵也进行分解，将参数个数降低到2∗n∗F个，模型如下：

$${\hat{r}}_{ui}=\frac{1}{\sqrt{|N(u)|}}\sum _{j\in N(u)}{x}_i^T{y}_j=\frac{1}{\sqrt{|N(u)|}}{x}_i^T\sum _{j\in N(u)}{y}_j$$

这里 $x_i、y_i$ 是两个 $F$ 维的向量。由此可见，该模型用 $x_i^T{y}_j$ 代替了 $w_{ij}$ ，从而大大降低了参 数的数量和存储空间。 再进一步，我们可以将前面的LFM和上面的模型相加，从而得到如下模型:

$${\hat{r}}_{ui}=\mu +b_u+b_i+p_u{q}_i^T+\frac{1}{\sqrt{|N(u)|}}{x}_i^T\sum _{j\in N(u)}{y}_j$$
Koren又提出，为了不增加太多参数造成过拟合，可以令 $x=q$ ，从而得到终的SVD++模型:
$${\hat{r}}_{ui}=\mu +b_u+b_i+q_i^T\left(p_u+\frac{1}{\sqrt{|N(u)|}}\sum _{j\in N(u)}{y}_j\right)$$

（5）基于图模型的协同过滤推荐

1.用户行为的二分图表示

用户的行为可以使用二分图表示，因此图的很多算法也应用到推荐系统之中，基本思想是将用户的行为数据表示为一系列的二元组（u，i），表示用户u对物品i的行为，这样可以将用户的行为表现为一个二分图。

下图是一个简单的用户物品二分图模型，其中圆形节点代表用户，方形节点代表物品，圆形节点和方形节点之间的边代表用户对物品的行为。比如图中用户节点A和物品节点a、b、d相连，说明用户A对物品a、b、d产生过行为。

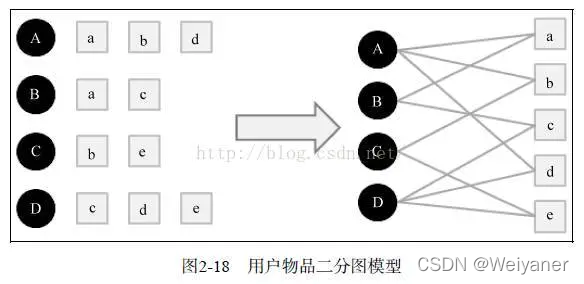
2.PageRank算法

基于用户行为二分图，给用户推荐物品就可以转换为计算顶点u和其他物品顶点之间的相关性，然后根据相关性的高低给未关联物品节点继续进行排序。这也就是图的排名问题，Google的PageRank算法可以解决这个问题，
PageRank的两个基本假设:

• 数量假设： 一个page接收其他页面的入链数量越多，那么这个界面就越重要。
• 质量假设： 指向该网页的网页质量越高，这个界面越重要。

利用以上两个假设，PageRank算法刚开始赋予每个网页相同的重要性得分，通过迭代递归计算来更新每个页面节点的PageRank得分，直到得分稳定为止

相关性高的顶点一般具有以下特点：

• 两个顶点之间连接路线很多
• 两个顶点之间的路径很短
• 两个顶点之间的路径不会经过出度很高的顶点

PageRank是Larry Page 和 Sergey Brin设计的，用来衡量特定网页相对于搜索引擎中其他网页的重要性的算法，其计算结果作为Google搜索结果中网页排名的重要指标。网页之间通过超链接相互连接，互联网上不计其数的网页就构成了一张超大的图。

PageRank假设用户从所有网页中随机选择一个网页进行浏览，然后通过超链接在网页直接不断跳转。到达每个网页后，用户有两种选择：到此结束或者继续选择一个链接浏览。

算法令用户继续浏览的概率为d，用户以相等的概率在当前页面的所有超链接中随机选择一个继续浏览。

这是一个随机游走的过程。
当经过很多次这样的游走之后，每个网页被访问用户访问到的概率就会收敛到一个稳定值。这个概率就是网页的重要性指标，被用于网页排名。算法迭代关系式如下所示：

$$\mathrm{PR}(\mathrm{i})=\frac{1-d}{N}+d\sum _{j\in \mathrm{in}(i)}\frac{PR(j)}{|\mathrm{out}(j)|}$$
上式中PR(i)是网页的访问概率（也就是重要度），d是用户继续访问网页的概率，N是网页总数。in(i)表示指 向i
网页的网页集合，out(j)表示网页j指向的网页集合。

3.公式解释

$基本思想$

如果网页T指向网页A，那么认为A具有一定的重要性，假设PR（T）是网页T的重要性，out（j）是j的出链集合。就可以将T的重要程度分给A一部分，记作。

$$\frac{PR(j)}{|out(j)|}$$

因此简单得重要度计算就是累加求和：

$$\sum _{j\in in(i)}\frac{PR(j)}{|out(j)|}$$

$修正的PageRank：$

由于存在一些出链为0，也就是那些不链接任何其他网页的网， 也称为孤立网页，使得很多网页能被访问到。因此需要对 PageRank公式进行修正，即在简单公式的基础上增加了阻尼系数（damping factor）q， q一般取值q=0.85。

其意义是，在任意时刻，用户到达某页面后并继续向后浏览的概率。 1- q= 0.15就是用户停止点击，随机跳到新URL的概率.

最后，即所有这些被换算为一个百分比再乘上一个系数q。由于上面的算法没有子页面的PageRank会是0。所以，Google通过数学系统给了每个页面一个最小值。
$$PR(A)=\frac{1-q}{N}+q\left(\frac{PR(B)}{L(B)}+\frac{PR(C)}{L(C)}+\frac{PR(D)}{L(D)}+\cdots \right)$$
也就是：
$$PR(i)=\frac{1-d}{N}+d\sum _{j\in \mathrm{in}(i)}\frac{PR(j)}{|\mathrm{out}(j)|}$$

关于PageRank，详细看这篇文章

4.PersonalRank算法

对于推荐系统，我们需要计算的是物品节点相对于某一个用户节点u的相关性。

Standford的Haveliwala于2002年在他《Topic-sensitive pagerank》一文中提出了PersonalRank算法，该算法能够为用户个性化的对所有物品进行排序。它的迭代公式如下：
PR ⁡ ( i ) = ( 1 − d ) r i + d ∑ j ∈ in ⁡ ( i ) P R ( j ) ∣  out  ( i ) ∣ r i = { 1 i = u 0 i ≠ u

$$\begin{aligned} &\operatorname{PR}(\mathrm{i})=(1-\mathrm{d}) r_{i}+d \sum_{j \in \operatorname{in}(i)} \frac{P R(j)}{\mid \text { out }(i) \mid} \\ &r_{i}= \begin{cases}1 & i=u \\ 0 & i \neq u\end{cases} \end{aligned}$$ ​PR(i)=(1−d)ri​+dj∈in(i)∑​∣ out (i)∣PR(j)​ri​={10​i=ui​=u​​

和PageRank的区别仅仅在于使用ri替换了1/N。也就是说从不同点开始的概率不同。

算法过程：

假设要给用户u进行个性化推荐，可以从用户u对应的节点Vu开始在用户物品二分图上进行随机游走。

游走到任何一个节点时，首先按照概率α决定是继续游走，还是停止这次游走并从Vu节点开始重新游走。如果决定继续游走，那么就从当前节点指向的节点中按照均匀分布随机选择一个节点作为游走下次经过的节点。

这样，经过很多次随机游走后，每个物品节点被访问到的概率会收敛到一个数。最终的推荐列表中物品的权重就是物品节点的访问概率。

• 缺点
  PersonalRank每次都需要在全图迭代，所以时间复杂度非常高。
• 解决办法
  减少迭代次数，在收敛前停止。会影响精度，但影响不大。
  从矩阵论出发，重新设计算法。

---

上一篇：推荐系统（3）——个性化推荐系统架构
下一篇：推荐系统（5）——推荐算法2（POLY2-FM-FFM-GBDT-MLR）