- 1大数据毕业设计Python+Django旅游景点评论数据采集分析可视化系统 NLP情感分析 LDA主题分析 bayes分类 旅游爬虫 旅游景点评论爬虫 机器学习 深度学习 人工智能 计算机毕业设计_旅游评论 机器学习
- 2LDA模型训练与得到文本主题、困惑度计算(含可运行案例)_lda = gensim.models.ldamodel.ldamodel
- 3自然语言处理中的单词向量:全局向量(GloVe)_输出全局向量是什么意思
- 4今日arXiv最热大模型论文:从Twitter动态预测论文学术不端,人大发布
- 5「IDEA」使用IDEA创建Android项目无法下一步_idee安装安卓sdk时不能下一步
- 6TCN(Temporal Convolutional Network,时间卷积网络)
- 7Python VScode配置
- 8【深度强化学习】(4) Actor-Critic 模型解析,附Pytorch完整代码_actor critic
- 9机器人机械臂运动学——逆运动学解算_逆运动学求解
- 10基于Django在线酒店宾馆点评系统设计与实现(Pycharm+Python+Mysql)
电能质量扰动信号数据介绍与分类-Python实现_python给电压数据做分类
赞
踩

往期精彩内容:
电能质量扰动信号数据介绍与分类-Python实现-CSDN博客
Python电能质量扰动信号分类(一)基于LSTM模型的一维信号分类-CSDN博客
Python电能质量扰动信号分类(二)基于CNN模型的一维信号分类-CSDN博客
Python电能质量扰动信号分类(三)基于Transformer的一维信号分类模型-CSDN博客
Python电能质量扰动信号分类(四)基于CNN-BiLSTM的一维信号分类模型-CSDN博客
Python电能质量扰动信号分类(五)基于CNN-Transformer的一维信号分类模型-CSDN博客
基于FFT + CNN -Transformer时域、频域特征融合的电能质量扰动识别模型-CSDN博客
引言
本文详细介绍电能质量扰动分析,利用Python生成数据集,并提供对应的研究思路。在参考IEEE Std1159-2019电能质量检测标准与文献[1,2]的基础上构建了扰动信号的模型。
1 电能质量PQD扰动简介
1.1 PQD来源
在电力系统中,特别是智能电网和微电网环境中存在许多固有的和相关的问题。以微电网为载体接入新能源发电,电动汽车,储能系统和各类负载等,是未来主动配电网的发展趋势。该发展趋势能有效缓解能源紧缺和环境污染等问题,但同时也会恶化配电网中电能质量问题,其主要原因有两个方面:一是电网中电力电子元器件的占有量提升,二是自然资源的随机特性[3]。

1.2 PQD定义
电能质量指的是电力系统中电压、电流和频率等参数的稳定性和纯净度。在电力系统中,可能会出现各种电能质量扰动,这些扰动可能由于设备故障、电力负载变化、电力系统故障或其他外部因素引起。
2 PQD分类
2.1 单一扰动简介
(1)正常电压:

(2)电压暂降
电压暂降指电压幅值在 0.1~0.9pu 范围,持续时间为 0.5T~1min 的电能质量扰动现象,其中 T 为基频周期。通常以剩余电压或暂降深度和持续时间为描述特征。IEEE 标准定义的暂降深度是剩余电压占额定参考电压的百分比。本质上都是对暂降的幅度进行描述。电压暂降通常与系统短路故障有关,但也会因启动或投切重载引起。
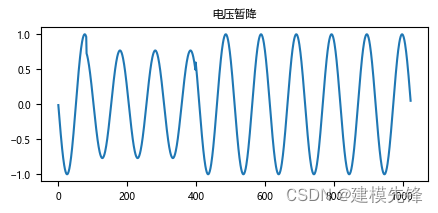
(3)电压暂升
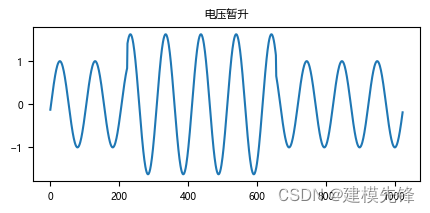
(4)谐波
谐波是一个周期电气量的正弦波分量,其频率为基波频率的整数倍。当谐波分量与基波分量结合时,就会产生波形畸变。谐波电流主要由电力电子设备使用时向电网注入,继而在电网传输线阻抗上产生了谐波压降,进一步导致电压畸变。

(5)电压波多(闪变)
电压波动是指电压波形包络的一系列随机电压波动,幅值在范围内变化:0.95~1.05pu 。用电压幅值和波动频度来表述其特征。定义电压变动值中相邻两个极值的变化称为一次电压波动,把单位时间内电压波动的次数称为电压波动频度。轧钢机、绞车的频繁启动和焊机的间歇通电等,会引起规律性的周期电压波动;电弧炉等波动性负荷则会引起供电点出现连续、随机、无规律的电压波动。

(6)暂态脉冲
脉冲瞬变指电压或电流或两者,在稳态情况下突然以非电源频率发生单一极性的变化。通常以上升或下降时间为描述特征,因此又可将脉冲瞬变细分为纳秒、微秒和毫秒 3 个级别。纳秒级脉冲瞬变持续时间一般小于 50ns,微秒级脉冲瞬变持续时间一般为 50ns~1ms,毫秒级脉冲瞬变持续时间一般大于 1ms。引起脉冲瞬变最主要的原因是闪电。
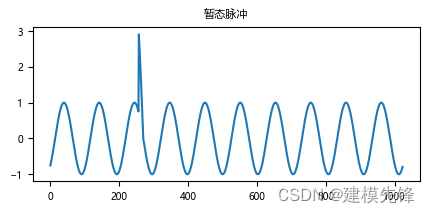
(7)振荡暂态
振荡瞬变指电压或电流或两者,在稳态情况下突然以非电源频率发生双极性的变化。其中频率低于 5kHz,持续时间为 0.3~50ms,电压幅值为0~4pu 范围的一般称为低频振荡瞬变;频率处于5~500kHz,持续时间约 20µs,电压幅值 0~8pu 范围的一般称为中频振荡瞬变;频率处于 0.5~5MHz,持续时间约为 5µs,电压幅值为 0~4pu 范围的一般称为高频振荡瞬变。通常以持续时间、振荡频率和电压幅值为描述特征。引起振荡瞬变的主要原因是接地故障或负荷/开关切换瞬态等。
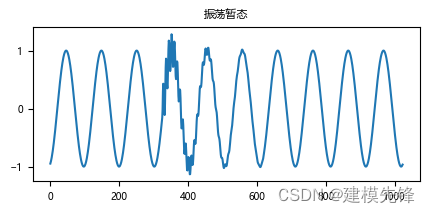
(8)电压中断
电压中断指电压幅值低于 0.1pu,持续时间为 0.5T~1min 的电能质量扰动现象。通常以电压幅值和持续时间为描述特征。IEEE 中将电压中断按持续时间的不同分为暂时(0.5T~3s)和短时(3s~1min)中断。电压中断通常是由电力系统故障、设备故障等造成。
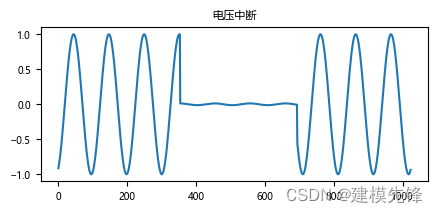
(9)电压缺口
电压缺口是当电流从一相转换到另一相时,电力电子设备的正常操作引起的周期性电压扰动。电压陷波表示一种特殊情况,它是周期性的,但频率含量相当高。因此,它具有可以被视为瞬态和谐波失真的属性。由于缺口是连续发生的(稳态),因此可以通过受影响电压的谐波频谱来表征。然而,由于与缺口相关的高频分量,用典型的谐波测量设备可能无法对其进行表征。
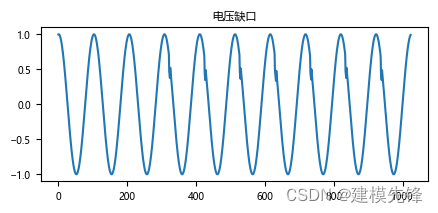
(10)电压尖峰
电压尖峰的特点是持续数十微妙及高达几百伏的电压,由雷击或负载阶跃的感应耦合产生,属于浪涌电压里的一种。电机、电容器和功率转换设备(如变速驱动器)是产生尖峰电压的主要因素。
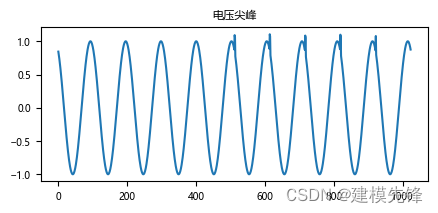
2.2 复合扰动简介
复合扰动定义为:包含两种(含两种)以上单 一扰动的电能质量扰动形式。复合扰动的组合形式 可以根据表1和表2中的划分形式进行考校[4]:
-
按表1所示分属暂态、稳态的情况除外,同一参数不可能同时发生两种不同方式的突变;
-
不同参数可以同时发生突变;
-
加性扰动的存在不受参数变 化的限制。
-
较为常见的复合扰动信号包括谐波与各种暂态扰动的复合、两种暂态扰动的复合、各种稳 态扰动的复合等,且都有着各自的特点。
表1 暂态和稳态划分

表2 参数突变划分

部分扰动信号类型波形图如下所示:
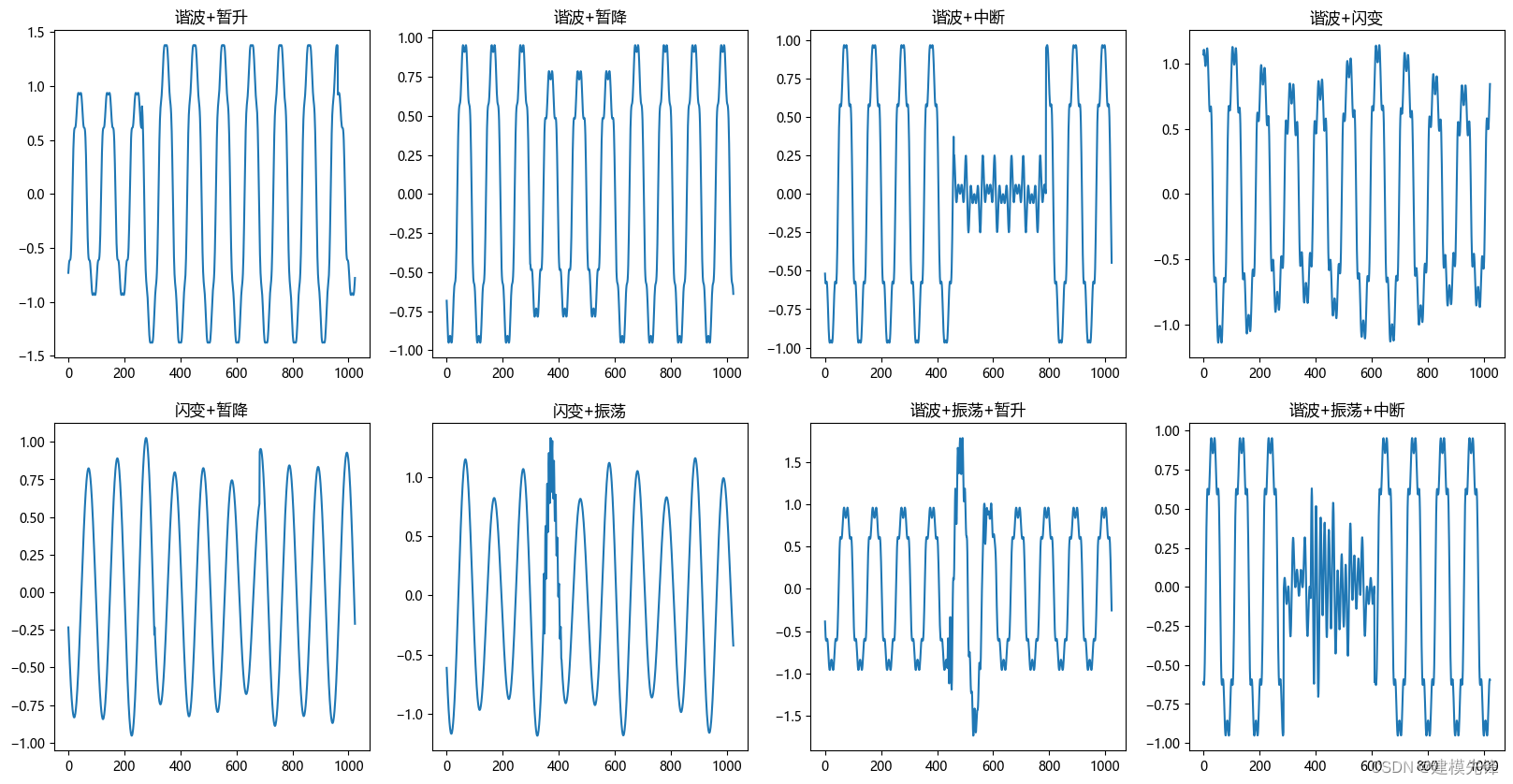
3 基于Python的电能扰动信号数据生成
3.1 基础知识
-
电压频率:f,50Hz
-
电压周期:t= 1/f , 0.02s
-
采样周期:采样时间周期 T = 10t, 一般默认10个t,即0.2s
-
采样频率:一般默认2560Hz, 或者5120Hz,或者其他(自定义,比较灵活)
怎么理解采样频率,可以先从自己需要的信号序列长度出发,比如我想得到的信号序列长度为512,那么采样周期为0.2s,就对应512个采样点,那么1秒就采样2560个点,所以采样频率就为2560Hz,因为序列长度需要根据自己的偏好和任务来决定,所以不固定统一,很多论文的采样频率也自然不尽统一。(可以灵活设定)
3.2 Python实现扰动信号数据生成
参照IEEE Std1159-2019标准和论文公式模型,以及前面讲解的内容,用Python进行仿真生成信号数据
以正常信号公式为例:
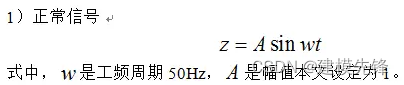
第一步,导入相关包,用于生成信号
import numpy as npimport randomimport matplotlibmatplotlib.rc("font", family='Microsoft YaHei')第二步,设置参数
# 1. 正常信号w = 2 * np.pi / 0.02# 幅值A = 1#频率Hz,每秒采样2560次,对应序列长度为512f = 2560 # 在0~2pi之间随机一个数字表示采样开始TimeStrat = np.random.random() * 2 * np.pi# 生成一个时间间隔TimeInterval,它是从0到f/5的一个等差数列,步长为1/fTimeInterval = np.arange(0, (f / 5) / f, 1 / f) 第三步,按照公式生成信号
# 每次信号起始点设置不相同t = TimeStrat + TimeInterval # 生成信号z = A * np.sin(w * t)第四步,绘制信号图波形图
plt.figure(figsize=(5,2))plt.plot(z)plt.title('正常信号', fontsize=8)plt.show()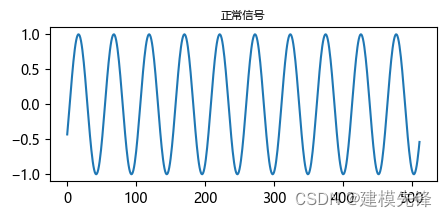
一般在做实验中会给数据添加白噪声,添加70db~20db不等的噪声来增强数据的真实性,检验模型的抗噪能力和泛化能力
信噪比(Signal-to-Noise Ratio,SNR)
信噪比(Signal-to-Noise Ratio,SNR)是衡量信号与噪声比例的指标。信噪比的单位是分贝(dB),它描述了信号与噪声的相对强度。较高的信噪比表示信号更强、噪声更弱,较低的信噪比表示噪声相对较强。
-
当信噪比较高时,信号的功率远大于噪声的功率,噪声对信号的影响较小,因此添加噪声后,信号的变化可能不太明显。这就是为什么在添加50 dB信噪比的噪声后,原始信号看起来没有太大的变化。
-
而当信噪比较低时,噪声的功率相对较高,噪声对信号的影响较大,因此添加噪声后,信号的变化更加明显。这解释了为什么在添加20 dB信噪比的噪声后,原始信号看起来有较大的变化。
注意,信噪比的值只表示信号和噪声之间的相对强度,对于人眼来说,直观地感知信号变化的大小也受到多种因素的影响,包括信号的频率、幅度和噪声的性质等。因此,即使信噪比较高,也可能存在一些细微的变化,但通常难以直接观察到。
第五步,添加高斯白噪声
# 信噪比设置为 20 dBsnr_db = 20 # 计算信号功率signal_power = np.mean(z ** 2) # 计算噪声功率noise_power = signal_power / (10 ** (snr_db / 10)) # 生成高斯白噪声,均值为0,标准差为噪声功率的开平方noise = np.random.normal(0, np.sqrt(noise_power), z.shape) z_with_noise = z + noise生成噪声图像:
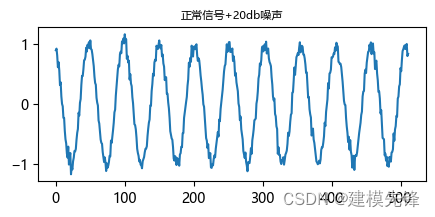
3.3 按照公式,生成其他单一信号
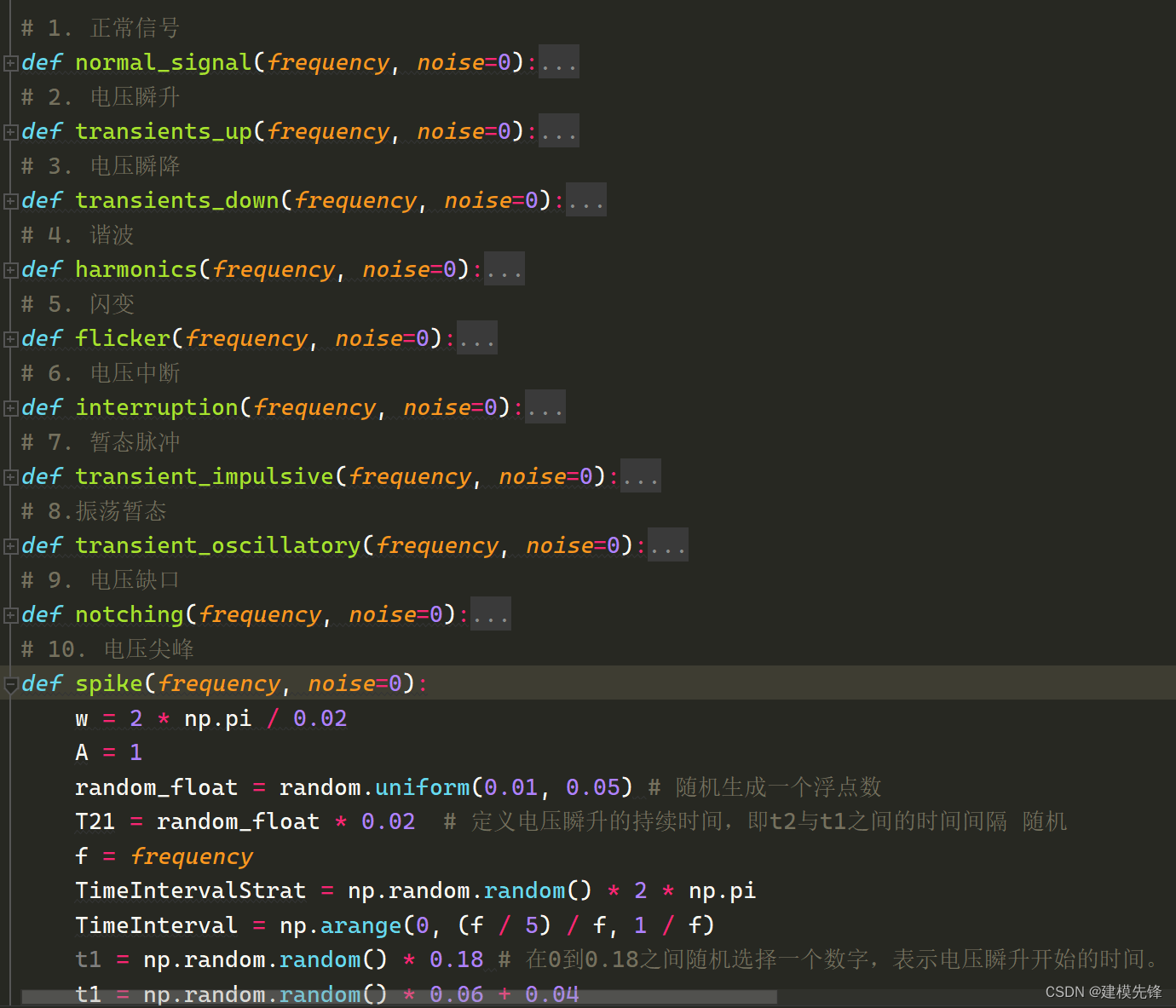
生成对应的波形图:
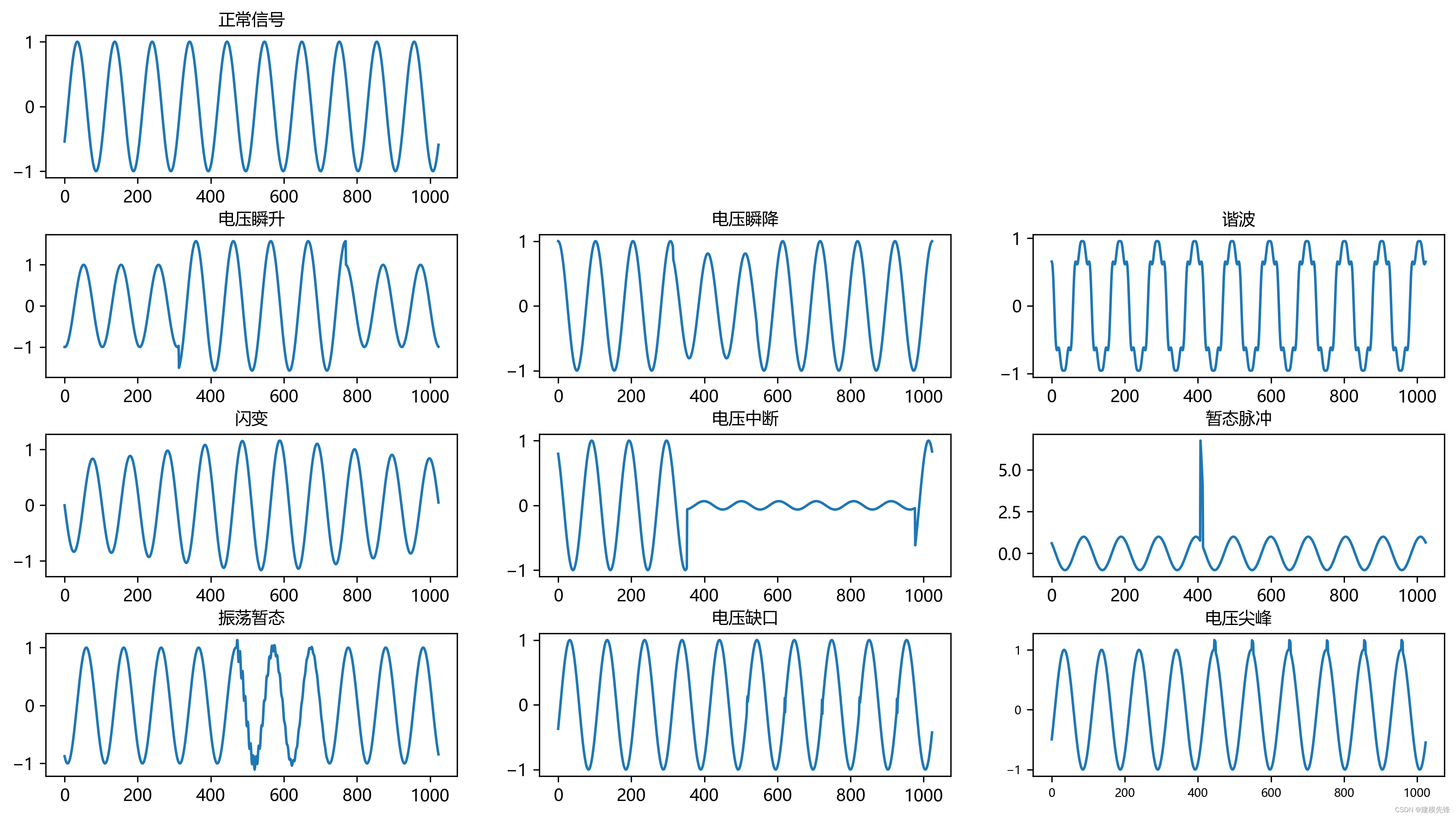
3.4 按照公式,生成复合信号
复合信号种类有多种组合方式,根据自己的模型和任务设置适当的类型数量;比如文献[3]选取了63种信号,有的论文就选取10种单一信号的,也有加上复合信号16分类的、20分类的、25分类的不尽统一。
根据文献[1, 2]1生成15种复合PQD信号,
二重扰动:即暂降+谐波(D11)、暂升+谐波(D12)、中断+谐波(D13)、闪变+谐波(D14)、谐波+脉冲(D15)、暂升+暂态振荡(D16)、闪变+暂升(D17)、闪变+暂降(D18)、闪变+暂态振荡(D19)、闪变+暂态脉冲(D20)、闪变+中断(D21)、暂升+暂态振荡(22)
三重扰动:
谐波+振荡+暂降(D23)、谐波+振荡+中断(D24)、谐波+振荡+闪变(D25)
所研究的扰动模型基本频率为50 Hz,各参数在公式表规定范围之内随机生成。
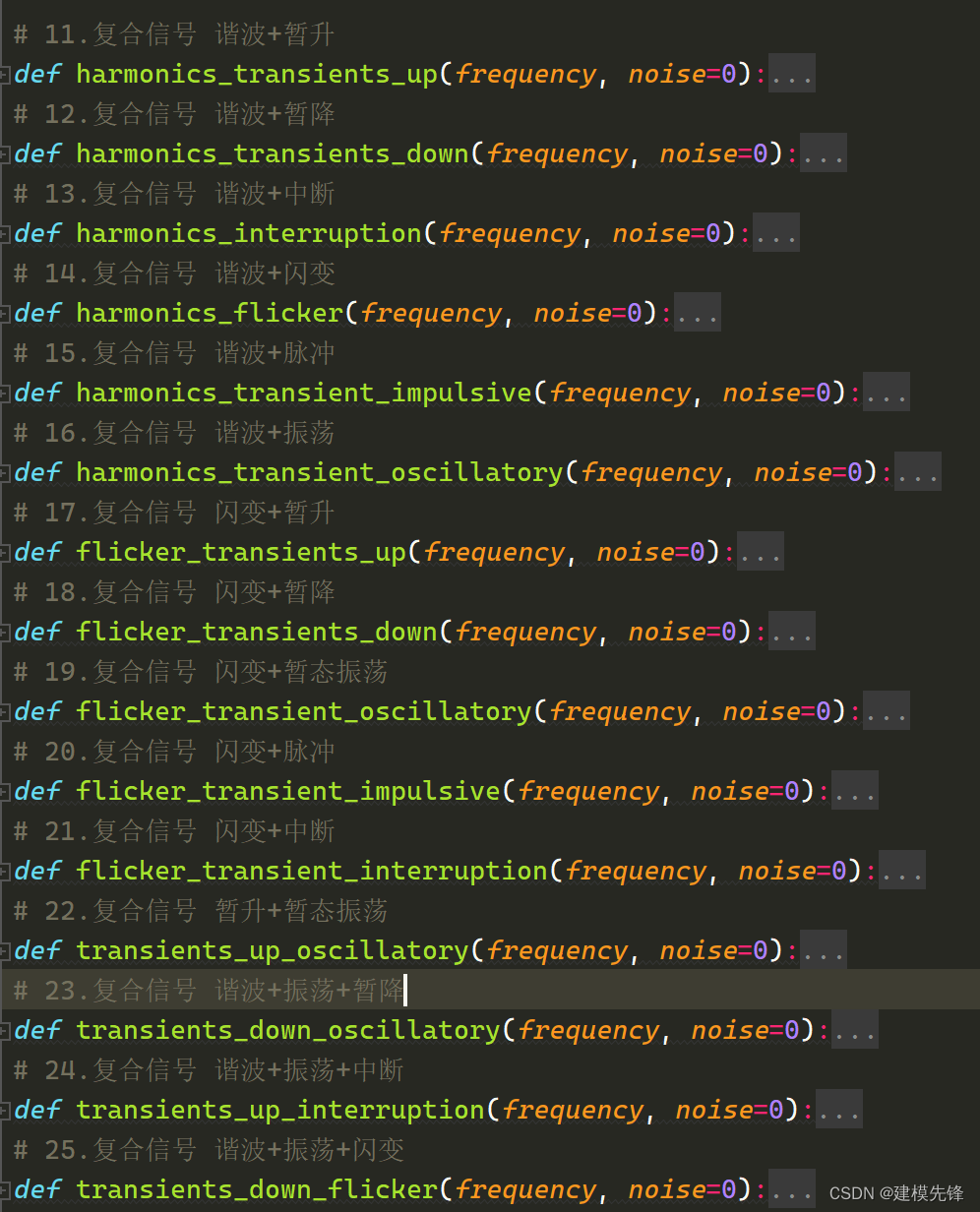
生成部分复合信号波形图如下所示:
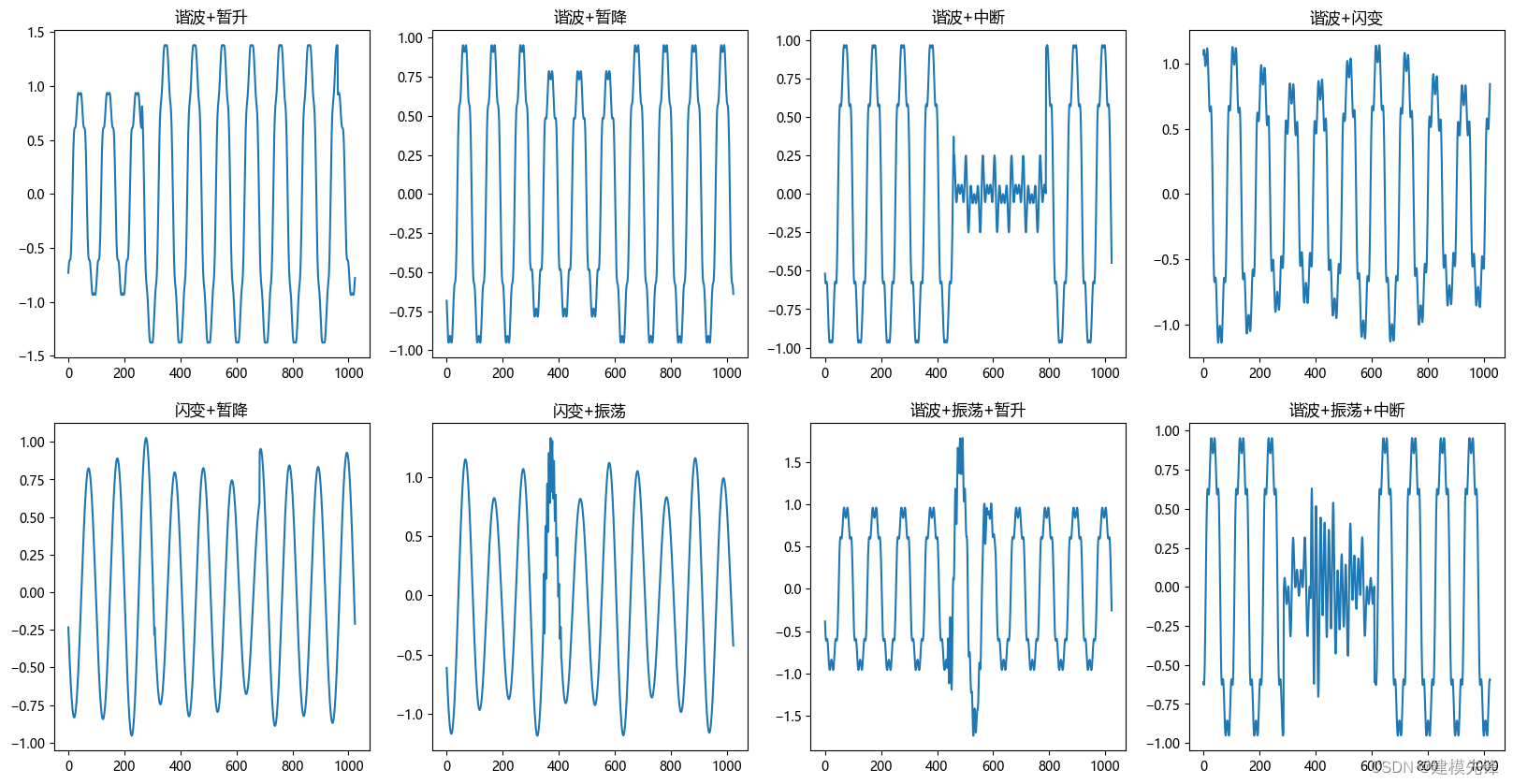
4 基于Python的扰动信号分类研究思路
4.1 关于扰动信号分类的方法探讨
第一类是对一维扰动信号数据进行分类
-
一是直接对一维扰动信号数据,添加分类标签进行处理,送进CNN、LSTM等网络进行分类;
-
二是先对一维扰动信号数据做一些变换、分解处理或者去噪,然后再进行分类;
第二类是把一维扰动信号数据转换为图像进行分类
-
一是转换为二维时序图进行分类;
-
二是转换为时频图像进行分类;
-
三是基于格拉姆角场(GAF)转换为二维图像进行分类;
比如二维时序图:
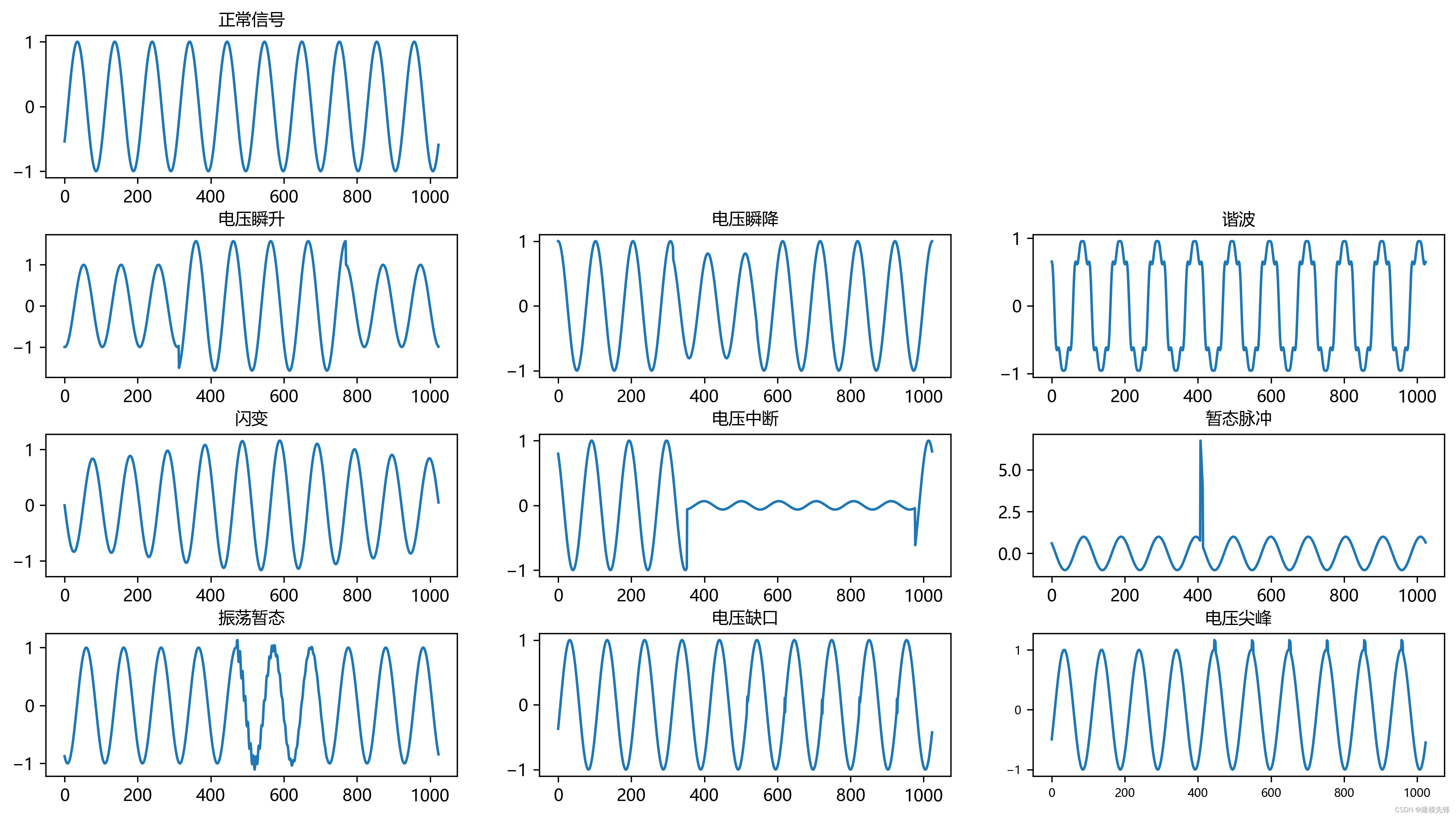
比如二维时频图像:
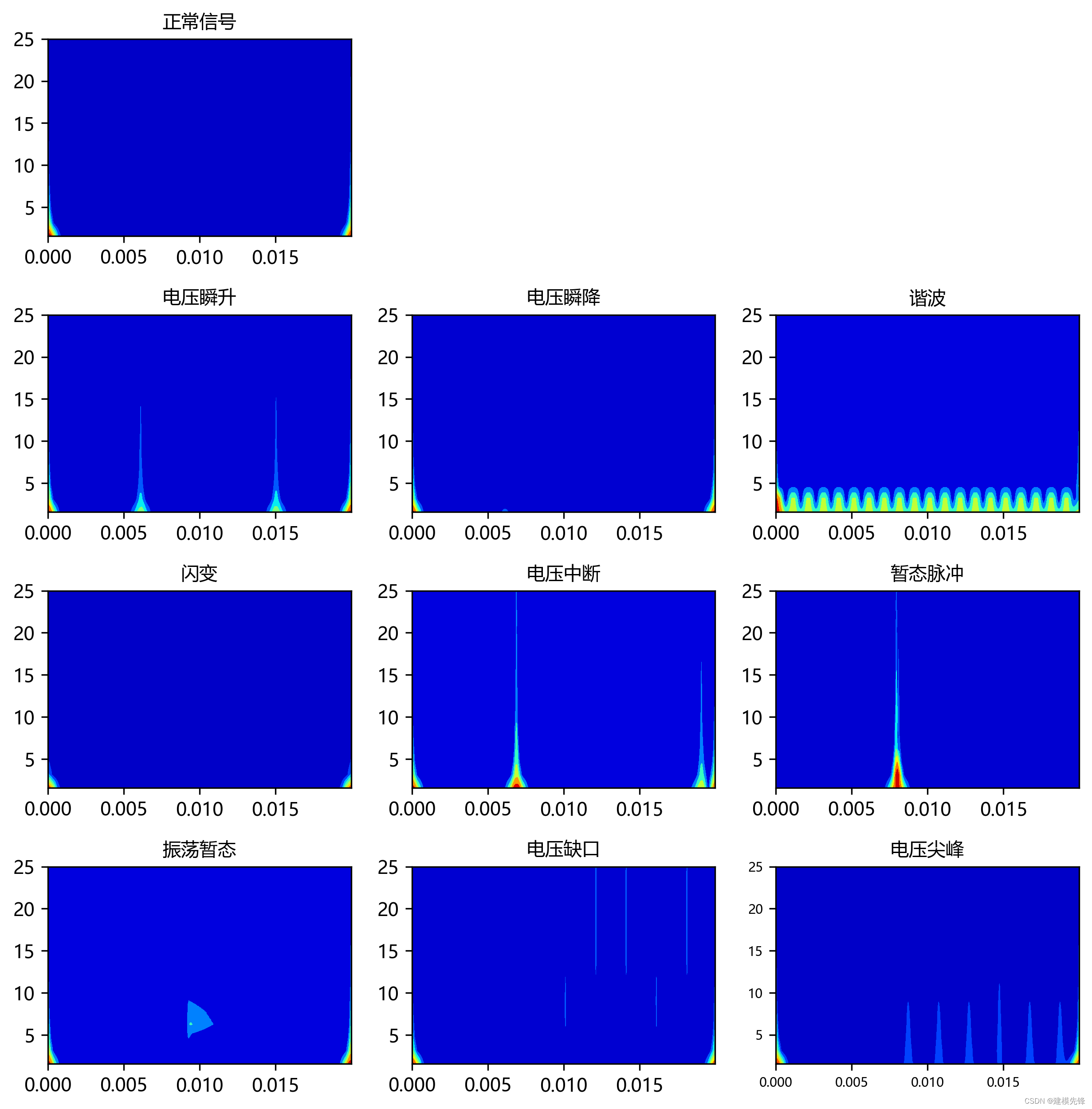 比如基于格拉姆角场(GAF)的二维图像:
比如基于格拉姆角场(GAF)的二维图像:

4.2 重点介绍关于直接对一维扰动信号分类的方法
以单一扰动信号10分类举例
第一步,生成样本数据,并添加标签:
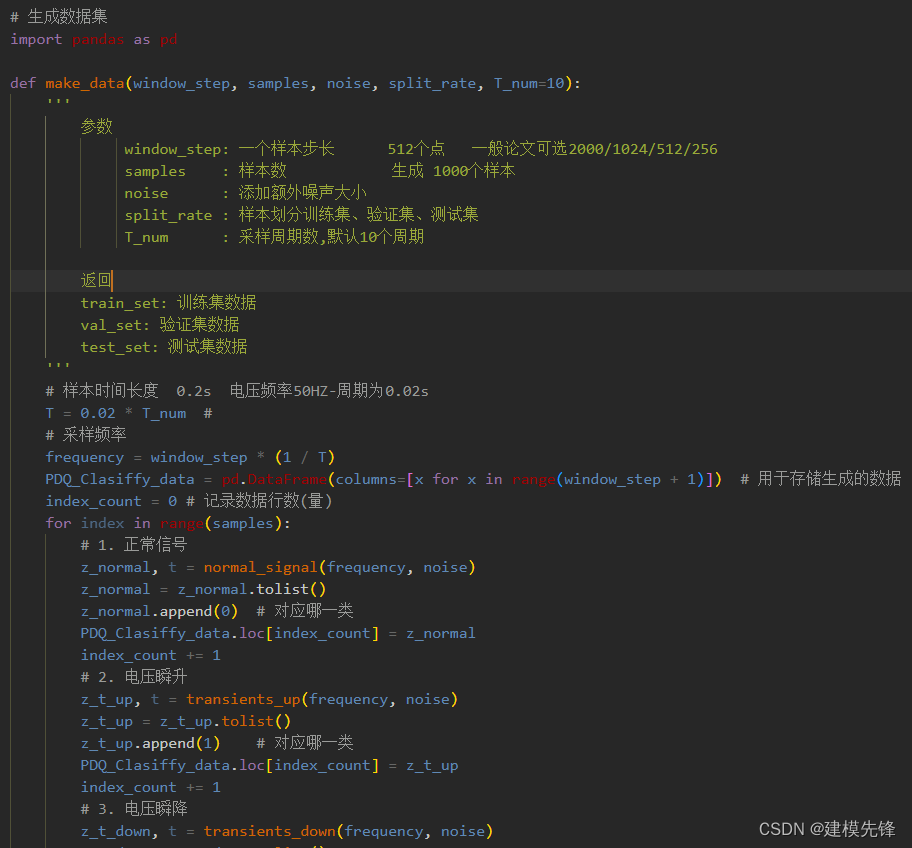
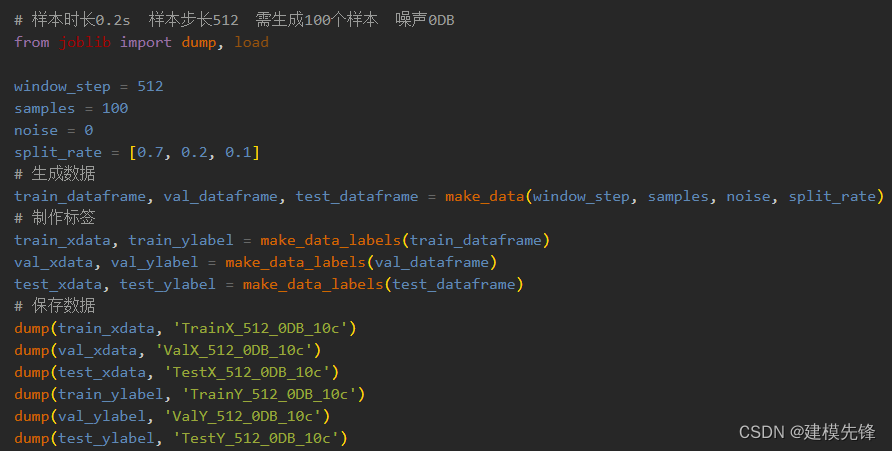
第二步,定义LSTM分类模型:
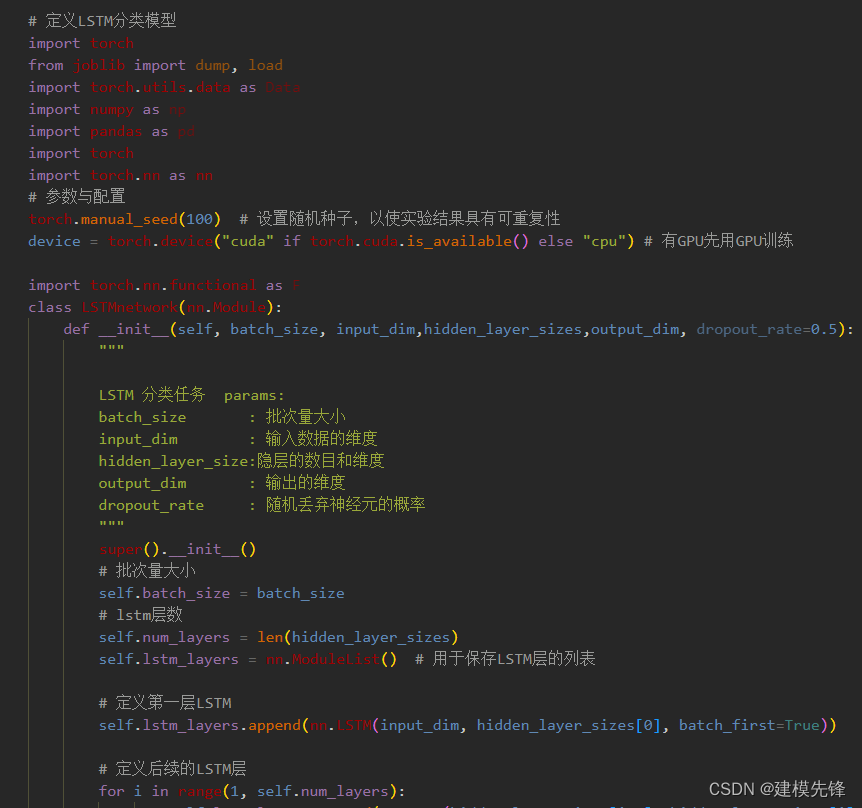
第三步,设置模型参数:
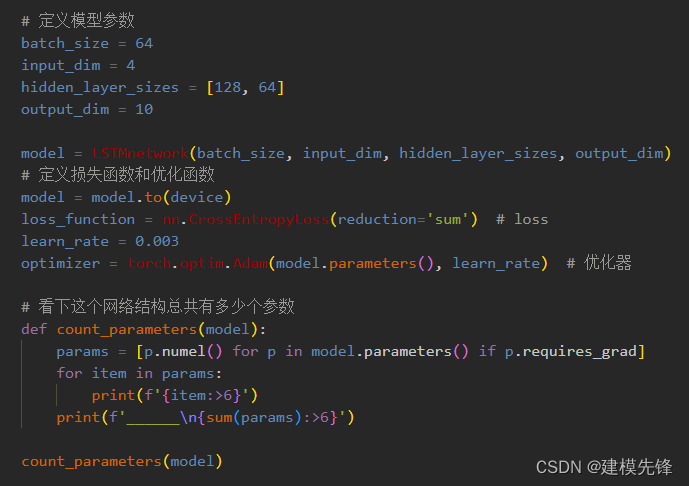
第四步,训练模型:
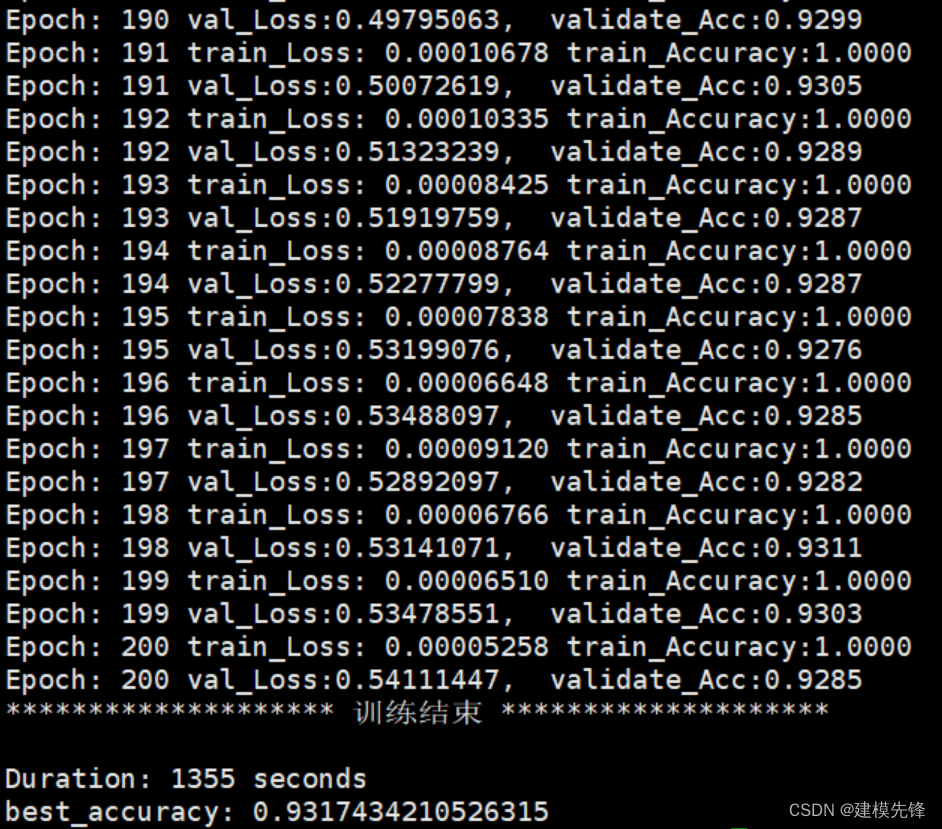
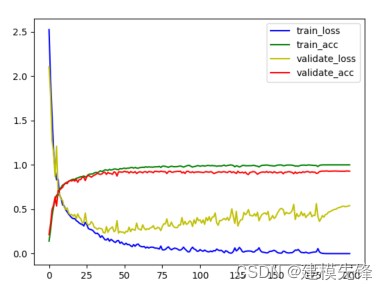
200个epoch,准确率将近93%,模型过拟合,进一步调整参数可以提升性能。
参考资料
[1]郑炜,林瑞全,王俊,等. 基于GAF与卷积神经网络的电能质量扰动分类[J]. 电力系统保护与控制,2021,49(11):97-104.
[2] 程志友,姜帅,程安然,等. 基于小样本的卷积神经网络电能质量扰动分类方法[J]. 淮北师范大学学报(自然科学版),2022,43(4):45-51.
[3]刘宇龙,崔宪阳,袁丁等.基于多级注意力机制融合的电能质量扰动点分类及时间定位方法研究[J].中国电机工程学报,2023,1-14.
[4]刘志刚,张巧革,张杨. 电能质量复合扰动分类的研究进展[J]. 电力系统保护与控制,2013(13):146-153.
如有文献内容版权问题,请联系博主删除。