什么是Attention机制以及Pytorch如何使用_attention pytorch

前言

看了网上大部分人做的，都是说一个比较长的项目（特别是机器翻译的多）。其实没有必要，很多人并不是想看一个大项目，只是想看看怎么用，并把Attention机制用到自己的任意一个项目中。下面来介绍之。

注意力概况

首先告诉大家，注意力这个词本身是一个非常高屋建瓴的词，其作用于两个东西，然后计算他们的注意力。

1. 两个东西是什么?随便你，比如可以是向量，可以是矩阵，可以是你想要的一切，不过，计算机中也只有向量和矩阵，因为计算机只能表示数字。一般是向量。
2. 有了两个东西之后，有一个统一而不可分割的问题，即：注意力是什么以及怎么计算？也是随便你定义。

下面我们将介绍的是我们通常用的注意力，即两个东西都是向量。但是区别在于上面的2，所以分成了标准注意力方式和变种注意力。

import numpy as np
import torch
1
2

提前剧透一下，Attention机制是要手动实现的，而且很简单，手动实现的好处在于灵活定义自己的注意力。即Attention机制并不是一个什么Module，然后你是一个调包侠，调来就用的。

标准注意力

两个向量的注意力计算方式如下：

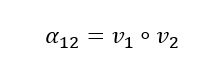
上述∘代表内积，下同。

不过，只计算两个向量的注意力通常没有什么用，因为现在是大数据时代，通常会有一大堆向量，假设我们有3个行向量如下：

a=np.random.randint(-1,2,(3,3))
print(a)
1
2

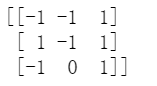
那么我们可以使用标准注意力计算注意力得到9个数。即第1个向量和第1个向量的注意力，第1个向量和第2个向量的注意力，第1个向量和第3个向量的注意力，第2个向量和第1个向量的注意力，。。。

如下：

a=np.matmul(a,a.T)
print(a)
1
2

上面第一行就是第一个向量和其他3个向量的所有注意力了。

我们发现，上述是对称矩阵，这是因为标准注意力的计算方式是对称的，两个向量是完全平等的关系和地位。下面的变种注意力可不一定是对称的哦。

不过，上述还没有归一化。标准的归一化是使用softmax进行归一化，即我们需要对每一行进行如下操作。

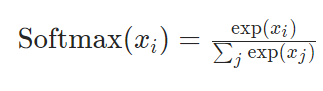
比如第一行归一化就是:先计算分母$s=exp6+exp7+exp6$，然后计算第一行的第一个数：$exp6/s$，其他类推。

import torch.nn.functional as tnf
a=torch.tensor(a,dtype=torch.float32)
b=tnf.softmax(a,dim=1)
print(b)
1
2
3
4

计算好了归一化的注意力之后，我们需要得到我们最终的目标，即得到新的向量，我们以得到新的第1个向量为例，怎么做？新的第1个向量=0.6652*旧的第1个向量+0.0900*旧的第2个向量+0.2447*旧的第3个向量。即：

b=b.numpy()
a=a.numpy()
c=np.matmul(b,a)
print(c)
1
2
3
4

至此，我们得到了我们想要的3个新的向量。

变种注意力

下面介绍一种，我见过的计算两个向量的注意力的方法，显然，其不是对称的。

上面两个向量需要拼接，另外，a是自己提前定义的常数。

我们还是以3个向量为例：

a=[1,-1,2,0,-1,-1]#定义的常数。
v=np.random.randint(-1,2,(3,3))
print(v)
1
2
3

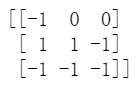
我们需要两个两个向量拼接在一起，从而获得到9个6维的向量。

v=torch.tensor(v,dtype=torch.float32)
print(v)
v_r=v.repeat_interleave(3,0)
print(v_rr)
v_rr=v.repeat(3,1)
print(v_r)
vv=torch.cat((v_r,v_rr),dim=1)
print(vv)
1
2
3
4
5
6
7
8

然后我们用拼接后的9*6乘以6维的向量a就得到了9个注意力。

a=[1,-1,2,0,-1,-1]
b=torch.matmul(vv,torch.tensor(a,dtype=torch.float32))
print(b)
print(b.view(3,3))
1
2
3
4

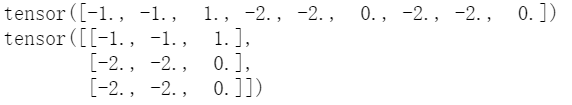
此时，第一行[-1,-1,1]就是第1个向量和其他向量的注意力，其他依次类推，然后，又是一样的归一化，然后得到新的3个向量，就不多说了。

QKV

Q:query
K:key
V:value

Q，K，V都是矩阵，而且任意。这个是前面所讲述的的扩展延申，上面一般被称作自注意力机制(self-attention)，即Q=K=V的情形。

对于Q，K，V任意的一般情形，我们计算注意力步骤如下：1.利用Q,K计算注意力，2.用1得到的注意力和V乘积，得到新的向量。

在前几节讲的自注意力机制中，其实Q=K=V=a，就是前面那个3*3的初始化矩阵。然后我们套用一下上述计算注意力步骤，发现其实和我们前几节的方法是一样的，所以说前几节是特例。

a=np.matmul(a,a.T)#利用Q=a,K=a计算注意力
b=tnf.softmax(a,dim=1)#注意力归一化
c=np.matmul(b,a)#注意力和V=a乘积
1
2
3

基于上面，我们扩展到一般注意力（Q,K,V任意）的情形。

比如：

q=np.random.randint(-1,2,(3,3))
print(q)
k=np.random.randint(-1,2,(3,3))
print(k)
v=np.random.randint(-1,2,(3,3))
print(v)
1
2
3
4
5
6

我们先做一个直观上的解释，升华理解。以矩阵q的第一行为例（其实q,k,v不一定都是3*3的矩阵，比如q可以是1*3)，q的第一行是我的东西，k就像是3个中间人（3行，分别负责3个交易市场）,v是k背后的3个交易市场。我们需要用我的东西查询k的3个中间人（3行），得到3个注意力，表示我的东西去3个交易市场交易的可能性，如果我的东西去交易市场1更能卖好价钱，那么注意力就会更高。然后，我们归一化，就得到了我们拿着我的东西去3个交易市场的概率。

这个时候，有软注意力和硬注意力。硬注意力就是选择概率最大的那个，然后去那个交易市场。举个例子，即归一化之后，还会进一步操作：
[0.2,0.3,0.5]->[0,0.1]
然后[0,0.1]与v矩阵相乘，得到的结果是第3个交易市场的值，即v的第3行，至此，我们得到了新值。

不过，软注意力才是我们用的最多的，其直接使用[0.2,0.3,0.5]与v矩阵相乘，所以是综合和3个交易市场的结果，其中第3个交易市场综合的最多，因为0.5最大嘛。虽然软注意力在我们举得这个交易市场例子里好像解释不通，但是绝大多数计算机场合都优于硬注意力，可以这么说，我们通常都直接使用软注意力。

回到q,k,v任意，同样，按照之前的计算注意力步骤，我们计算如下：

import torch.nn.functional as tnf
q,k,v=torch.tensor(q,dtype=torch.float32),torch.tensor(k,dtype=torch.float32),torch.tensor(v,dtype=torch.float32)
qk=torch.matmul(q,k.T)#q,k计算注意力
qk=tnf.softmax(qk,dim=1)#注意力归一化
qkv=torch.matmul(qk,v)#注意力和v乘积。
print(qk)
print(qkv)#新值，或者叫做查询结果。
1
2
3
4
5
6
7

应用

我们只说了如何使用注意力，但是大家肯定一头雾水，特别是对于新值，为什么要得到这个东西，这个东西代表什么，又该如何使用呢？这个你随便看一个比较简单的用了注意力机制的模型图就知道怎么使用了。

---

完结撒花

---