二叉搜索树(Binary Search Tree)（Java实现）_comparator cmp

1、二叉搜索树

1.1、 基本概念

二叉树的一个性质是一棵平均二叉树的深度要比节点个数N小得多。分析表明其平均深度为$\mathcal{O}(\sqrt{N})$,而对于特殊类型的二叉树，即二叉查找树(binary search tree),其深度的平均值为$\mathcal{O}(logN)$。

二叉查找树的性质： 对于树中的每个节点X，它的左子树中所有项的值小于X中的项，而它的右子树中所有项的值大于X中的项。

由于树的递归定义，通常是递归地编写那些操作的例程。因为二叉查找树的平均深度为$\mathcal{O}(logN)$，所以一般不必担心栈空间被用尽。

1.2、树的节点（BinaryNode）

二叉查找树要求所有的项都能够排序，有两种实现方式；

1. 对象实现接口 Comparable, 树中的两项使用compareTo方法进行比较；
2. 使用一个函数对象，在构造器中传入一个比较器；

本篇文章采用了构造器重载，并定义了myCompare方法，使用了泛型，因此两种方式都支持，在后续的代码实现中可以看到。

节点定义：

    /**
     * 节点
     *
     * @param <AnyType>
     */
    private static class BinaryNode<AnyType> {
        BinaryNode(AnyType theElement) {
            this(theElement, null, null);
        }

        BinaryNode(AnyType theElement, BinaryNode<AnyType> left, BinaryNode<AnyType> right) {
            element = theElement;
            left = left;
            right = right;
        }

        AnyType element; // the data in the node
        BinaryNode<AnyType> left; // Left child
        BinaryNode<AnyType> right; // Right child
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

1.3、构造器和成员变量

    private BinaryNode<AnyType> root;
    private Comparator<? super AnyType> cmp;

    /**
     * 无参构造器
     */
    public BinarySearchTree() {
        this(null);
    }

    /**
     * 带参构造器，比较器
     *
     * @param c 比较器
     */
    public BinarySearchTree(Comparator<? super AnyType> c) {
        root = null;
        cmp = c;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

关于比较器的知识可以参考下面这篇文章：
Java中Comparator的使用
关于泛型的知识可以参考下面这篇文章：
如何理解 Java 中的 <T extends Comparable<? super T>>

1.3、公共方法（public method）

主要包括插入，删除，找到最大值、最小值，清空树，查看元素是否包含；

    /**
     * 清空树
     */
    public void makeEmpty() {
        root = null;
    }

    public boolean isEmpty() {
        return root == null;
    }

    public boolean contains(AnyType x){
        return contains(x,root);
    }

    public AnyType findMin(){
        if (isEmpty()) throw new BufferUnderflowException();
        return findMin(root).element;
    }

    public AnyType findMax(){
        if (isEmpty()) throw new BufferUnderflowException();
        return findMax(root).element;
    }

    public void insert(AnyType x){
        root = insert(x, root);
    }

    public void remove(AnyType x){
        root = remove(x,root);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

1.4、比较函数

如果有比较器，就使用比较器，否则要求对象实现了Comparable接口；

    private int myCompare(AnyType lhs, AnyType rhs) {
        if (cmp != null) {
            return cmp.compare(lhs, rhs);
        } else {
            return lhs.compareTo(rhs);
        }
    }
1
2
3
4
5
6
7

1.5、contains 函数

本质就是一个树的遍历；

    private boolean contains(AnyType x, BinaryNode<AnyType> t) {
        if (t == null) {
            return false;
        }

        int compareResult = myCompare(x, t.element);
        if (compareResult < 0) {
            return contains(x, t.left);
        } else if (compareResult > 0) {
            return contains(x, t.right);
        } else {
            return true;
        }
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

1.6、findMin

因为二叉搜索树的性质，最小值一定是树的最左节点,要注意树为空的情况。

    /**
     * Internal method to find the smallest item in a subtree
     * @param t the node that roots the subtree
     * @return node containing the smallest item
     */
    private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t) {
        if (t == null) {
            return null;
        }
        if (t.left == null) {
            return t;
        }
        return findMin(t.left);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

1.7、findMax

最右节点；

    /**
     * Internal method to find the largest item in a subtree
     * @param t the node that roots the subtree
     * @return the node containing the largest item
     */
    private BinaryNode<AnyType> findMax(BinaryNode<AnyType> t){
        if (t == null){
            return null;
        }
        if (t.right == null){
            return t;
        }
        return findMax(t.right);
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14

1.8、insert

这个主要是根据二叉搜索树的性质，注意当树为空的情况，就可以加入新的节点了，还有当该值已经存在时，默认不进行操作；

    /**
     * Internal method to insert into a subtree
     * @param x the item to insert
     * @param t the node that roots the subtree
     * @return the new root of the subtree
     */
    private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t){
        if (t == null){
            return new BinaryNode<>(x,null,null);
        }
        int compareResult = myCompare(x,t.element);

        if (compareResult < 0){
            t.left = insert(x,t.left);
        }
        else if (compareResult > 0){
            t.right = insert(x,t.right);
        }
        else{
            //Duplicate; do nothing
        }

        return t;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

1.9、remove

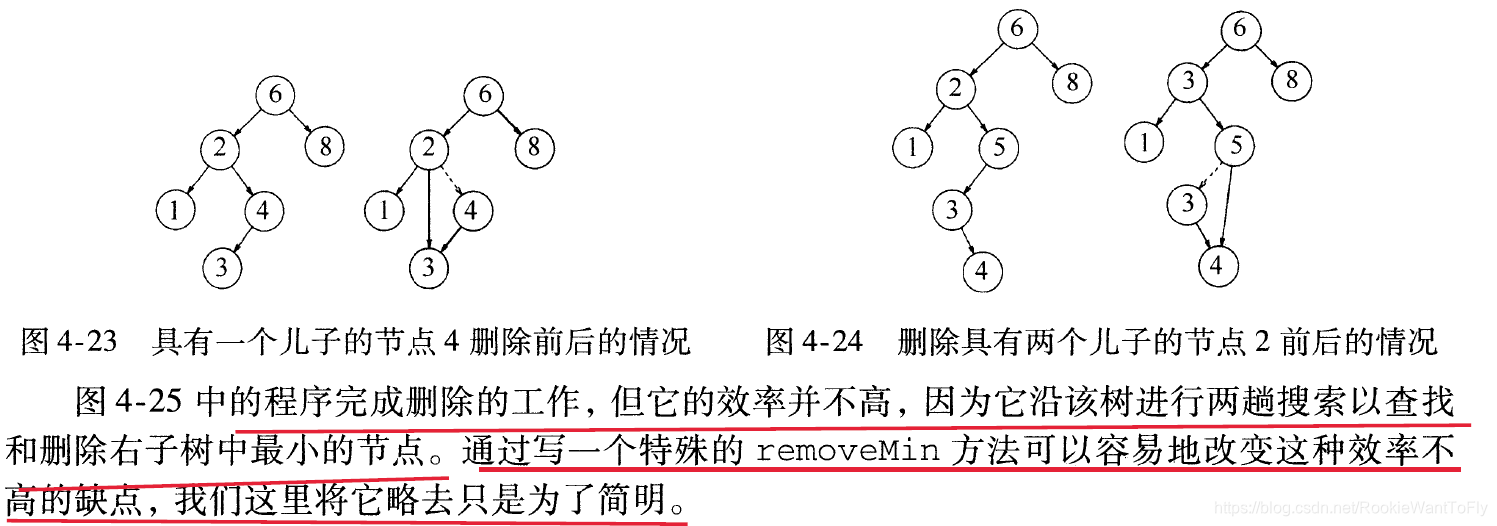
注意当空树时，返回null；
最后一个三元表达式，是在之前已经排除掉节点有两个儿子的情况下使用的。

    /**
     * Internal method to remove from a subtree
     * @param x the item to remove
     * @param t the node that roots the subtree
     * @return the new root of the subtree
     */
    private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t){
        if (t == null){
            return t; // Item not found ,do nothing
        }
        int compareResult = myCompare(x,t.element);

        if (compareResult < 0){
            t.left = remove(x,t.left);
        }
        else if (compareResult > 0){
            t.right = remove(x,t.right);
        }
        else if (t.left !=null && t.right!=null){
            //Two children
            t.element = findMin(t.right).element;
            t.right = remove(t.element,t.right);
        }
        else
            t = (t.left !=null) ? t.left:t.right;
        return t;
    }
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

二、完整代码实现（Java）

/**
 * @author LongRookie
 * @description: 二叉搜索树
 * @date 2021/6/26 19:41
 */


import com.sun.source.tree.BinaryTree;

import java.nio.BufferUnderflowException;
import java.util.Comparator;

/**
 * 二叉搜索树
 */
public class BinarySearchTree<AnyType extends Comparable<? super AnyType>> {

    /**
     * 节点
     *
     * @param <AnyType>
     */
    private static class BinaryNode<AnyType> {
        BinaryNode(AnyType theElement) {
            this(theElement, null, null);
        }

        BinaryNode(AnyType theElement, BinaryNode<AnyType> left, BinaryNode<AnyType> right) {
            element = theElement;
            left = left;
            right = right;
        }

        AnyType element; // the data in the node
        BinaryNode<AnyType> left; // Left child
        BinaryNode<AnyType> right; // Right child
    }

    private BinaryNode<AnyType> root;
    private Comparator<? super AnyType> cmp;

    /**
     * 无参构造器
     */
    public BinarySearchTree() {
        this(null);
    }

    /**
     * 带参构造器，比较器
     *
     * @param c 比较器
     */
    public BinarySearchTree(Comparator<? super AnyType> c) {
        root = null;
        cmp = c;
    }

    /**
     * 清空树
     */
    public void makeEmpty() {
        root = null;
    }

    public boolean isEmpty() {
        return root == null;
    }

    public boolean contains(AnyType x){
        return contains(x,root);
    }

    public AnyType findMin(){
        if (isEmpty()) throw new BufferUnderflowException();
        return findMin(root).element;
    }

    public AnyType findMax(){
        if (isEmpty()) throw new BufferUnderflowException();
        return findMax(root).element;
    }

    public void insert(AnyType x){
        root = insert(x, root);
    }

    public void remove(AnyType x){
        root = remove(x,root);
    }




    private int myCompare(AnyType lhs, AnyType rhs) {
        if (cmp != null) {
            return cmp.compare(lhs, rhs);
        } else {
            return lhs.compareTo(rhs);
        }
    }

    private boolean contains(AnyType x, BinaryNode<AnyType> t) {
        if (t == null) {
            return false;
        }

        int compareResult = myCompare(x, t.element);
        if (compareResult < 0) {
            return contains(x, t.left);
        } else if (compareResult > 0) {
            return contains(x, t.right);
        } else {
            return true;
        }
    }

    /**
     * Internal method to find the smallest item in a subtree
     * @param t the node that roots the subtree
     * @return node containing the smallest item
     */
    private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t) {
        if (t == null) {
            return null;
        }
        if (t.left == null) {
            return t;
        }
        return findMin(t.left);
    }

    /**
     * Internal method to find the largest item in a subtree
     * @param t the node that roots the subtree
     * @return the node containing the largest item
     */
    private BinaryNode<AnyType> findMax(BinaryNode<AnyType> t){
        if (t == null){
            return null;
        }
        if (t.right == null){
            return t;
        }
        return findMax(t.right);
    }

    /**
     * Internal method to remove from a subtree
     * @param x the item to remove
     * @param t the node that roots the subtree
     * @return the new root of the subtree
     */
    private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t){
        if (t == null){
            return t; // Item not found ,do nothing
        }
        int compareResult = myCompare(x,t.element);

        if (compareResult < 0){
            t.left = remove(x,t.left);
        }
        else if (compareResult > 0){
            t.right = remove(x,t.right);
        }
        else if (t.left !=null && t.right!=null){
            //Two children
            t.element = findMin(t.right).element;
            t.right = remove(t.element,t.right);
        }
        else
            t = (t.left !=null) ? t.left:t.right;
        return t;
    }

    /**
     * Internal method to insert into a subtree
     * @param x the item to insert
     * @param t the node that roots the subtree
     * @return the new root of the subtree
     */
    private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t){
        if (t == null){
            return new BinaryNode<>(x,null,null);
        }
        int compareResult = myCompare(x,t.element);

        if (compareResult < 0){
            t.left = insert(x,t.left);
        }
        else if (compareResult > 0){
            t.right = insert(x,t.right);
        }
        else{
            //Duplicate; do nothing
        }

        return t;
    }

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202