稀疏表示字典学习KSVD算法详解与MATLAB实现（超清晰！_k-svd: an algorithm for designing overcomplete dic

论文题目
K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation
这篇论文的去噪效果还是很不错的，个人认为凡是学习图像去噪/复原这一方向的都应该学习。

我这篇文章是很久之前写的了，借鉴了一些大佬的理解，但由于时间久远，忘了哪部分是借鉴的谁，所以若有雷同请指出，我会重新编辑，附上大佬的原文链接。
准确的说，我是看了很多大佬对这篇论文的讲解，自己再琢磨琢磨，整合出了这篇文章，自认为是理解透彻了，希望对你有用。
我把maltab代码上传到资源了，无需积分即可下载，欢迎与我讨论。
ksvd算法matlab code

前言：什么是稀疏信号

稀疏信号：若信号仅有限非零采样点，而其他采样点均为零（或接近于零），则称信号是稀疏的。
但是自然图像信号中，稀疏的情况是极少的，因为尽管有的地方值很小，但是并不为零，因此另一种概念“可压缩的”就被提出来，其定义是：如果在不丢失全部（大部分）信息的前提下，信号经过任何变换后是稀疏的，也就是说信号在某个变换域是稀疏的，那么可以称之为可压缩信号。
简单来说，可压缩的≈可稀疏的。

自然图像多数是可压缩信号。其中含噪图像是可稀疏的，噪声通常是不可稀疏的。

一、稀疏表示

稀疏表示（Sparse Representation）也叫作稀疏编码（Sparse Coding）,就是用字典中元素的线性组合去表示测试样本。

如上图所示，D是训练好的过完备字典（行数小于列数），通过稀疏编码，可以得到稀疏向量x，在重建过程中，利用字典D和稀疏向量x相乘，就可以用对应的第3,7,14个原子来线性表示原图像，稀疏向量x中不为0的个数是有限的，因此其表示是稀疏的。

补充知识：稀疏表示能够去噪的原因

对图像进行稀疏表示的过程可以看作对图像提取特征，可以认为含噪（观测）图像是由无噪（原始）图像和噪声合成的图像，而观测图像被认为是可稀疏的，即可以通过有限个原子来表示，而噪声是随机的不可稀疏的，即不可以通过有限个原子表示，因此通过观测图像去提取图像的稀疏成分，也就是只能提取出无噪图像的特征，再用这些稀疏成分来重构图像，在这个过程中，噪声被处理为观测图像和重构图像之间的残差，在重构过程中残差被丢弃，从而达到去噪的效果。

补充知识：使用过完备字典的原因

为什么要使用过完备的字典，或者说要在非正交的空间进行投影呢？
对于一组正交基而言，它们可以准确而唯一地表示空间中的任何向量，而且这些向量间没有冗余（因为正交），正是因为严格的正交限制，因此正交基的展开简单，但是稀疏性不够理想，因为严格正交的基往往只能表示图像的某一个特征而不能够同时表示其他特征，因此正交基的稀疏性不及非正交基（过完备字典）。

稀疏表示又称为稀疏编码，这个过程可以被视为特征提取的过程，可以看作把目标信号投影到一组非正交的基构成的空间中，而在每个基上投影的系数，就是稀疏编码。这组非正交的基向量中，每一个基向量被称为一个原子，这些原子（列向量）可以构成一个过完备字典。

二、字典学习

字典学习也可以理解为稀疏表示。字典学习指的是学习字典D。从矩阵分解角度，看字典学习过程：给定样本数据集Y，Y的每一列表示一个样本；字典学习的目标是把Y矩阵分解成D、X矩阵：

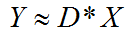
假设现在有了一个N*T的过完备字典 D，一个要表示的对象y（要还原的图像），求一套系数x，使得y=Dx，这里y是一个已知的长为N的列向量，x是一个未知的长为T的列向量，解方程。

这是一个T个未知数，N个方程的方程组，T>N，所以是有无穷多解的。

举个例子：N=5, T=8

这里可以引出一个名词，ill-posed problem（不适定问题），即有多个满足条件的解，无法判断哪个解更加合适，比如图像去噪，从噪声图中提取干净图，在哪种情况下重构出的图像最清晰呢？于是需要做一个约束。
同时满足约束条件：X尽可能稀疏，误差尽可能小。（误差是指含噪图像和重构图像之间的残差，也就是噪声。）
同时D的每一列是一个归一化向量。
D称之为字典，D的每一列称之为原子；X称之为编码矢量、特征、稀疏矩阵；字典学习可以有三种目标函数形式
(1)第一种形式：

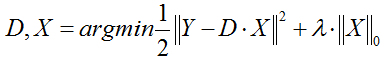
这种形式因为L0难以求解，所以很多时候用L1正则项替代近似。
(2)第二种形式：

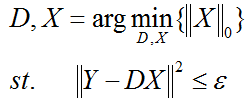
ε 是重构误差所允许的最大值。
(3)第三种形式：

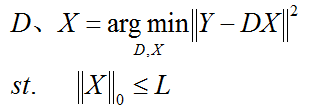
L是稀疏度约束参数，上面三种形式相互等价。

三、KSVD算法概述

给定原始样本矩阵Y，Y的每一列表示一个样本，求解字典D，字典D的每一列称为原子，用d_k表示。为什么叫做k-svd，因为综合了k-means 和SVD 的思想。

字典的初始化可以选取样本集中的K个原子作为最原始的过完备字典，也可以使用一个固定的字典，比如DCT字典。
稀疏表示分为两个阶段：
第一阶段：稀疏编码
利用模型：

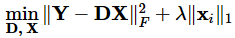
（形式1、2都是带有约束的优化问题，我们选用无约束优化问题便于计算，即形式1，由于1-范数更加便于求解，把式中的0-范数改为1-范数，即向量元素绝对值之和）
此时的字典是固定的（不更新字典），利用OMP算法，计算得到稀疏编码矩阵X，在得到X后，进入第二阶段。
第二阶段：字典学习
X编码矩阵已经已知了，现在开始逐列更新字典。
我们仅更新字典的第k列（字典共K列！稀疏矩阵共K行！），记d_k为字典D的第k列向量，记x_T^k为稀疏矩阵X的第k行向量，那么对于模型的前半部分，有

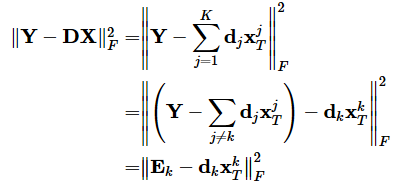
上式中残差

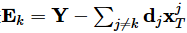
此时优化问题可以变形为：

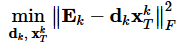
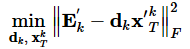
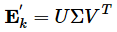
补充知识：奇异值分解（SVD）算法

以这种方式依次更新每一列原子和每一行稀疏编码，直到迭代完成。
算法流程：

仿真结果