- 1机器学习之增强学习DQN(Deep Q Network)
- 2idea 切换git仓库_在 IntelliJ IDEA 中这样使用 Git,效率提升2倍
- 3pod的生命周期
- 4使用docker在linux上安装mysql_linux docker 安装mysql
- 5深度学习01-tensorflow开发环境搭建_深度学习环境搭建 tensorflow
- 6Centos7 安装Git-cola
- 7Redis数据类型--Set类型详解及应用_redis set int
- 8Mac如何使用python创建Excel文件,并进行内容写入_mac电脑python操作写入数据
- 9vue-element-admin 的 npm install 报错npm ERR code 128 npm ERR An unknown git error occurred_vueelement-admin install 128
- 10Python2.7 xlrd读取、xlwt写入、xlutils读写Excel表格内容_xlrd 2.7
全代码分享|R语言孟德尔随机化怎么做?TwoSampleMR包MR一套标准流程_孟德尔随机化r语言
赞
踩
1.前言
孟德尔随机化(Mendelian randomization,MR)是一种利用基因变异作为工具变量来评估暴露与结果之间因果关系的统计方法。
它基于这样的原理:基因变异是在出生前就随机分配给个体的,类似于在随机对照试验中随机分配治疗,因此可以帮助区分因果关系和简单相关性。孟德尔随机化通常用于观察性数据,以确定一个特定的生物标志物、行为或其他暴露是否真正地影响了健康结果,而不是仅仅与之相关。通过这种方法,研究者可以减少混杂因素的影响,避免了传统观察性研究中常见的一些偏差。
1.1 成立条件
孟德尔随机化方法的关键在于三个基本假设的成立:
- 相关性假设(Relevance assumption):所选的遗传变异与暴露因素必须有明确的关联。这意味着这些遗传变异能够作为影响暴露水平的可靠指标。
- 独立性假设(Independence assumption):遗传变异与任何影响结果的混杂因素必须独立。基于孟德尔遗传定律,遗传变异在受精时随机分配给后代,这个随机分配过程保证了其与后天环境因素的独立性。
- 排他性假设(Exclusion restriction assumption):遗传变异对结果的影响只能通过其对暴露的影响来体现,不应存在其他路径。这意味着遗传变异与结果之间的关联完全是通过暴露因素介导的。
孟德尔随机化的实施通常需要大量的基因组数据,包括与暴露因素和结果变量相关的遗传变异信息。通过统计分析这些数据,研究者可以估计出暴露与结果之间的因果关系大小。
这种方法在流行病学和遗传流行病学领域尤其有用,特别是在探索疾病的潜在风险因素时。不过,孟德尔随机化研究的解释需要谨慎,因为违反上述任一假设都可能导致估计的偏误。此外,该方法还受限于可用的遗传变异信息和样本大小。
1.2 三大要素
在孟德尔随机化研究中,主要涉及三个关键组成部分:暴露因素、结果,以及作为连接两者的桥梁的遗传变异。
暴露因素:这指的是可能对某个健康结果产生影响的任何因素,如生活方式、环境因素、生物标志物等。在孟德尔随机化中,研究人员试图评估这种暴露是否对结果具有因果效应。例如,暴露因素可以是饮酒量、体育锻炼、血压或血脂水平等。
结果:这是研究的终点,通常是健康相关的结果,如疾病发生、健康状况指标、生理测量值等。在孟德尔随机化研究中,结果是研究者试图了解其是否受到暴露因素的影响。例如,结果可以是心血管疾病、糖尿病、肥胖或寿命等。
遗传变异:在孟德尔随机化框架中,遗传变异是连接暴露因素和结果的关键。这些遗传变异(通常是单核苷酸多态性,SNPs)根据遗传原理,在人群中随机分布,与暴露因素具有相关性但又不受后天环境因素的影响。遗传变异作为工具变量,其作用是帮助研究者推断暴露因素与结果之间的因果关系,而不是仅仅描述它们之间的关联。这些遗传变异必须满足特定条件,即与暴露因素强相关、与混杂因素无关,且仅通过影响暴露因素来影响结果。
1.3 统计原理
孟德尔随机化分析中通常使用的是工具变量(IV)估计的数学框架。这个框架可以帮助我们理解如何通过遗传变异(作为工具变量)来估计一个暴露因素对结果的因果效应。下面是一个简化的版本,描述了这一过程中涉及的主要步骤和公式。
看起来你对LaTeX格式的数学公式表示很感兴趣!那么,按照你提供的官方格式,孟德尔随机化中的关键公式也可以这样优雅地展示:
-
第一阶段回归:
给定遗传变异 (Z) 对暴露因素 (X) 的影响可以表示为:
X = α + β Z X Z + ϵ X = \alpha + \beta_{ZX}Z + \epsilon X=α+βZXZ+ϵ
其中,(X) 代表暴露因素,(Z) 是遗传变异(工具变量),(\alpha) 是截距,(\beta_{ZX}) 表示遗传变异对暴露因素的影响程度,(\epsilon) 是误差项。 -
第二阶段回归:
调整后的暴露因素 (X) 对结果 (Y) 的影响可以通过下面的方程来估计:
Y = γ + β X Y X ^ + ν Y = \gamma + \beta_{XY}\hat{X} + \nu Y=γ+βXYX^+ν
这里,(Y) 表示结果变量,(\hat{X}) 是从第一阶段回归中得到的基于遗传变异的暴露因素预测值,(\gamma) 是截距,(\beta_{XY}) 是调整后的暴露因素对结果影响的因果效应系数,(\nu) 是误差项。 -
工具变量估计的因果效应:
暴露因素 (X) 对结果 (Y) 的因果效应可以通过下面的比率来估计:
β ^ X Y = Cov ( Z , Y ) Cov ( Z , X ) \hat{\beta}_{XY} = \frac{\text{Cov}(Z, Y)}{\text{Cov}(Z, X)} β^XY=Cov(Z,X)Cov(Z,Y)
其中,(\hat{\beta}_{XY}) 是通过遗传工具变异估计的暴露因素对结果影响的因果效应系数,(\text{Cov}(Z, Y)) 和 (\text{Cov}(Z, X)) 分别表示遗传变异与结果变量以及遗传变异与暴露因素之间的协方差。
另外可以看一下前一篇的文献分享:
两步法的双样本孟德尔随机化怎么做?2暴露因素+4风险因素+3结果
2.demo
这里复现的是教育年限对EC的影响
2.1 加载R包
library(devtools)
library(tidyr)
# devtools::install_github("MRCIEU/MRInstruments")
library(MRInstruments)
library(MendelianRandomization)
library(TwoSampleMR)
#install.packages("simex")
library(simex)
#install_github("rondolab/MR-PRESSO")
library(MRPRESSO)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
2.2 主要MR分析
mydata <- read.table("01mydata_edu_cancer.txt", header=T, sep="\t", check.names = F, stringsAsFactors = F) heterogeneity <- mr_heterogeneity(mydata) heterogeneity # id.exposure id.outcome outcome exposure method Q Q_df Q_pval # 1 ieu-a-1001 lAx3ZW outcome || id:ieu-a-1001 MR Egger 347.7875 362 0.6951200 # 2 ieu-a-1001 lAx3ZW outcome || id:ieu-a-1001 Inverse variance weighted 347.8263 363 0.7075905 ### 二选一 # 2.1 如果I2<25%或Q_P>0.05,使用固定效应的逆方差加权法(IVW) mr_results <- mr(mydata, method_list=c('mr_ivw_fe')) mr_results generate_odds_ratios(mr_results) # 2.2 如果I2>25%且Q_P<0.05,使用随机效应的逆方差加权法(IVW) mr_results <- mr(mydata, method_list=c('mr_ivw_mre')) mr_results generate_odds_ratios(mr_results)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
2.3 MR补充分析、多态性、验证
选择加权还是不加权取决于数据特性和分析目的,当所有基因-暴露估计的可变性(标准误)大致相同时,不加权的方法可能更为适用,反之则使用加权。
教大家一个更简单的方法:加权和不加权都做,选结果好的(P值更显著的),如果都显著则选择加权的,因为它还照顾到每个点的不确定性,更为全面
mr_results1 <- mr(mydata, method_list=c('mr_two_sample_ml', 'mr_egger_regression', "mr_simple_median", "mr_weighted_median", "mr_penalised_weighted_median", "mr_simple_mode", "mr_weighted_mode")) mr_results1 # 4.1 MR-Egger截距测试 mr_pleiotropy_test(mydata) mr_egger(mr_input(bx = mydata$beta.exposure, bxse = mydata$se.exposure, by = mydata$beta.outcome, byse = mydata$se.outcome)) # 4.2 MR多态性残差和异常值(MR-PRESSO)测试 # 运行MR-PRESSO全局方法 mr_presso(BetaOutcome = "beta.outcome", BetaExposure = "beta.exposure", SdOutcome = "se.outcome", SdExposure = "se.exposure", OUTLIERtest = TRUE, DISTORTIONtest = TRUE, data = mydata, NbDistribution = 1000, SignifThreshold = 0.05, seed = 123456) # 5.1 IVW radial: mr_ivw_radial mr(mydata, method_list=c("mr_ivw_radial")) # 5.2 Egger-SIMEXS mr_egger(mr_input(bx = mydata$beta.exposure, bxse = mydata$se.exposure, by = mydata$beta.outcome, byse = mydata$se.outcome)) BetaXG <- mydata$beta.exposure BetaYG <- mydata$beta.outcome seBetaXG <- mydata$se.exposure seBetaYG <- mydata$se.outcome BYG <- BetaYG * sign(BetaXG) # 预处理步骤,确保所有基因-暴露估计都是正的 BXG <- abs(BetaXG) # MR-Egger回归(未加权) Fit1 <- lm(BYG ~ BXG, x=TRUE, y=TRUE) mod.sim1 <- simex(Fit1, B=1000, measurement.error = seBetaXG, SIMEXvariable="BXG", fitting.method ="quad", asymptotic="FALSE") summary(mod.sim1) # MR-Egger回归(加权) Fit2 <- lm(BYG ~ BXG, weights=1/seBetaYG^2, x=TRUE, y=TRUE) mod.sim2 <- simex(Fit2, B=1000, measurement.error = seBetaXG, SIMEXvariable="BXG", fitting.method ="quad", asymptotic="FALSE") summary(mod.sim2) # IVW不加权 Fit3 <- lm(BYG ~ -1 + BXG, x=TRUE, y=TRUE) mod.sim3 <- simex(Fit3, B=1000, measurement.error = seBetaXG, SIMEXvariable="BXG", fitting.method="quad", asymptotic="FALSE") summary(mod.sim3) # IVW加权 Fit4 <- lm(BYG ~ -1 + BXG, weights=1/seBetaYG^2, x=TRUE, y=TRUE) mod.sim4 <- simex(Fit4, B=1000, measurement.error = seBetaXG, SIMEXvariable="BXG", fitting.method="quad", asymptotic="FALSE") summary(mod.sim4)
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
2.4 结果可视化
library(ggplot2) # 散点图 plot1 <- mr_scatter_plot(mr_results1, mydata) plot1 # 单个SNP森林图 res_single <- mr_singlesnp( mydata, parameters = default_parameters(), single_method = "mr_wald_ratio", all_method = c("mr_ivw", 'mr_two_sample_ml', "mr_weighted_median") ) significant_snps <- res_single[res_single$p < 0.05, ] # 只保留P<0.05 plot2 <- mr_forest_plot(significant_snps) plot2 # 留一法敏感性测试 single <- mr_leaveoneout(mydata) top_30 <- single[order(single$p), ][1:30, ] # 只保留P最小的前30个 plot3 <- mr_leaveoneout_plot(top_30) plot3 # 漏斗图 plot4 <- mr_funnel_plot(res_single) plot4
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
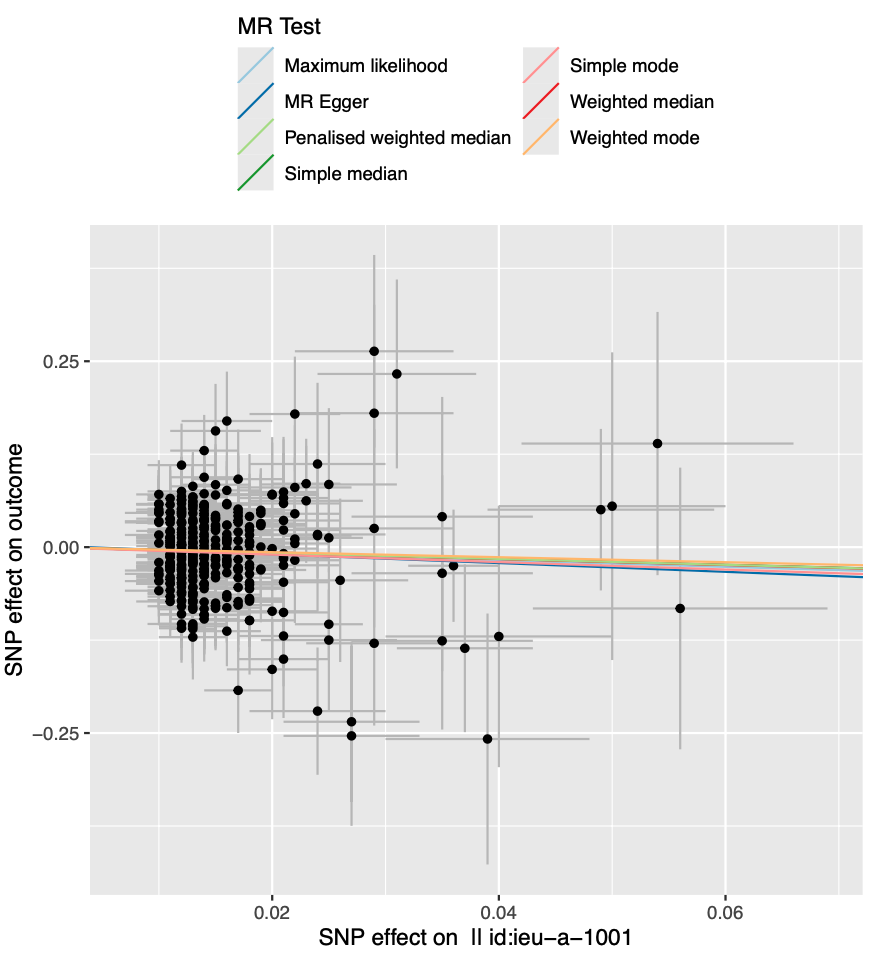 这个图是一个孟德尔随机化(MR)分析的散点图,通常用来评估遗传变异对某个健康结果的影响,并且试图解释这种影响是否有可能是因果的。在这个图中,每个点代表一个单独的遗传变异(通常是单核苷酸多态性,SNP)。横轴显示了每个SNP对暴露因素(例如某种生理指标或行为)的影响大小,而纵轴显示了每个SNP对结果(例如某种疾病或健康状况)的影响大小。每个点的位置表示了暴露和结果的关联,而点的大小可能表示了这种关联的统计权重,或者样本中该变异的频率。
这个图是一个孟德尔随机化(MR)分析的散点图,通常用来评估遗传变异对某个健康结果的影响,并且试图解释这种影响是否有可能是因果的。在这个图中,每个点代表一个单独的遗传变异(通常是单核苷酸多态性,SNP)。横轴显示了每个SNP对暴露因素(例如某种生理指标或行为)的影响大小,而纵轴显示了每个SNP对结果(例如某种疾病或健康状况)的影响大小。每个点的位置表示了暴露和结果的关联,而点的大小可能表示了这种关联的统计权重,或者样本中该变异的频率。
具体来说,图中展示了不同MR测试方法的结果线,这些线通常用于评估MR分析的整体趋势,这些方法可能包括:
| Type | Note |
|---|---|
| MR Egger | 这是一种检测和校正遗传仪表变量偏差的方法,用来评估遗传工具的有效性和存在潜在的选择性混杂。 |
| 加权中位数(Weighted median) | 这种方法允许部分遗传工具变量是无效的,但假定至少一半的工具变量信息是有效的。 |
| 惩罚加权中位数(Penalised weighted median) | 类似于加权中位数,但是通过对变异点施加惩罚来减少个别点的影响力,通常是为了控制极端值。 |
| 简单模式(Simple mode)和加权模式(Weighted mode) | 评估最常见的效应大小或者考虑了权重的效应大小。 |
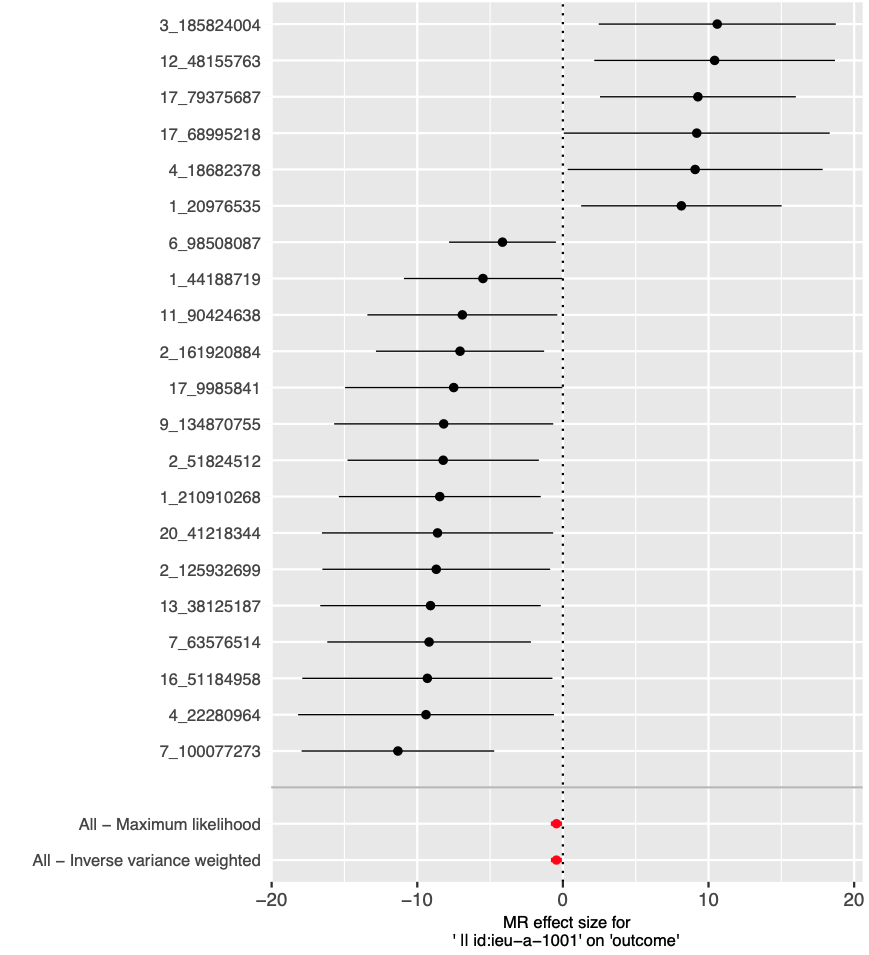
这张图是一个孟德尔随机化(MR)分析的森林图,展示了一系列遗传变异(单核苷酸多态性,SNPs)对某个结果的影响大小。在森林图中,每个水平线段代表一个SNP的估计效应及其95%置信区间,点代表估计效应的中心值。这种图形用于显示多个研究或分析的结果,并通常包括一个汇总的估计效应。
具体来说,左侧的数字可能是SNPs的编号或者是它们位于基因组上的位置(例如染色体上的特定位置)。中间的黑点代表每个SNP对结果的估计效应大小,而横向的线表示估计效应的置信区间;如果线越短,表示估计的不确定性越小。
在图的底部,有两个综合的点估计和置信区间:
| Type | Note |
|---|---|
| All – Maximum likelihood | 表示使用最大似然法对所有SNPs的效应大小进行综合估计。 |
| All – Inverse variance weighted | 表示使用逆方差加权法汇总所有SNPs的效应,这是最常用的汇总方法,给予不确定性较小的估计更大的权重。 |
红色的点估计和置信区间通常指示存在一个或多个离群值或强烈的偏离,这可能意味着那些特定的遗传变异与结果之间的关联可能受到了某些混杂因素或特定偏倚的影响。
该森林图提供了一个直观的方式来评估各个遗传变异对结果的可能影响,并且可以帮助研究人员判断是否有足够的证据支持遗传变异和结果之间的因果关系。在这种分析中,如果汇总估计的置信区间不包括零(垂直虚线),则通常被认为是有统计学意义的。在这张图中,大多数点的置信区间都跨过了零点线,暗示单个SNP的效应可能不具有统计学意义;但汇总效应点估计偏离零,表明可能存在暴露和结果之间的总体关联。然而,需要进一步的分析来确认这些发现。 这个图是一个“leave-one-out”敏感性分析的森林图,它用于孟德尔随机化(MR)研究中。在这种分析中,每次从分析中排除一个遗传变异(SNP),然后重新计算暴露因素对结果的影响,这样可以评估每个SNP对整体估计结果的影响程度。
这个图是一个“leave-one-out”敏感性分析的森林图,它用于孟德尔随机化(MR)研究中。在这种分析中,每次从分析中排除一个遗传变异(SNP),然后重新计算暴露因素对结果的影响,这样可以评估每个SNP对整体估计结果的影响程度。
在图中,每条水平线代表除了一个特定SNP之外的所有SNPs对结果影响的估计。横轴显示了估计效应的大小,点代表估计效应的中心值,线表示95%置信区间。
左侧的数字很可能是SNPs的标识符,可能是它们在基因组上的位置编号。
这种分析方法可以帮助研究人员识别任何可能异常影响整体分析结果的单个遗传变异。如果去除某个SNP后估计效应发生了显著变化,那么这个SNP可能是一个强烈的异常值或具有强烈的影响力。如果移除任何单一SNP后结果保持稳定,这表明MR分析的结果是稳健的,不会因单个SNP的异常而受到过度影响。
在图的底部,“All”项通常表示所有SNPs包含在内的总体效应大小估计。如果这个总体估计的置信区间不包括零点,这通常表明有一个统计上显著的效应。这张图显示的大多数点的置信区间都不包括零点,表明即使单独去除任何一个SNP,MR分析的结果也表明暴露可能对结果有显著影响。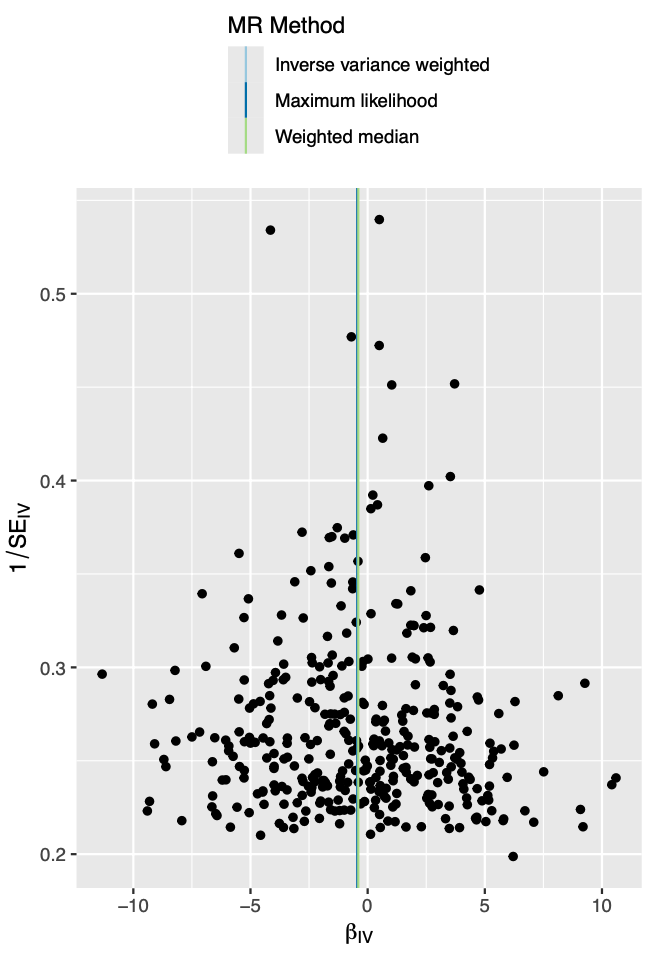
你提供的图是孟德尔随机化(MR)分析中常用的散点图,它用于展示遗传工具的效力(即遗传变异对暴露因素的影响大小)与它们对结果估计的因果效应大小之间的关系。
图中的横轴表示遗传变异对暴露因素的影响估计值,也就是效应大小。纵轴代表标准误差的倒数,用来表示每个估计的精确度;纵轴上方位置较高的点表明标准误差较小,估计的精确度更高。
在这种图中,我们通常会寻找是否存在漏斗形状,这样的形状意味着标准误差较大的估计(通常是效应大小较小的遗传变异)会更分散,而标准误差较小的估计则更集中。这有助于评估各个遗传变异作为工具变量时的稳健性和可信度。
图中还标注了不同的MR方法,例如逆方差加权(Inverse variance weighted)、最大似然(Maximum likelihood)和加权中位数(Weighted median)等,这些都是合成所有遗传变异影响的不同统计方法。
总体来说,这张图是在利用遗传信息探究特定暴露因素(如生活习惯、环境因素等)与健康结果(如某种疾病的风险)之间是否存在因果关系的工具。通过这种方法,研究人员可以在一定程度上避免传统观察性研究中常见的混淆因素,更可靠地揭示潜在的因果效应。
上述图注为GPT生成,实属无奈,纯代码分享但字数不够被定义为低质量文章,大家见谅
最后,示例数据仅供参考,笔者发现这个分析结果并不如意,权作教程示例数据使用,无实际意义!
有需要的小伙伴可以直接替换数据学起来吧~
下方后台回复MR1领取示例文件与代码



