- 1JWT VS OAuth2, 如何设计一个安全的API接口?,2024年最新网络安全高级工程师必备知识
- 2您与此网站之间建立的连接不安全(网站安全绿标显示方法)_您与此网站之间建立的连接不安全 csdn
- 3测试技能提升-接口测试6-pymysql增删改查,工具类封装、案例删除接口_pymysql 连接 查询 删除 封装
- 42022.8.17-jenkins远程over ssh的过程发现报错_jenkins outofmemoryerror
- 5【Android】Android 开机动画简述_android开机动画有两种方式
- 6【LeetCode】39.组合总和
- 7JAVA开启socket从流中读取2进制并转化为16进制_java serversocket 接收请求 二进制转十六进制
- 8github入门教程(非常详细)从零基础入门到精通,看完这一篇就够了_github操作
- 9英伟达GPU为什么那么火,一张图解GPU比CPU强多少?【猿界算力-AI学院】_英伟达图像处理
- 10C++架构之美:设计卓越应用_c++ 开发架构
机器学习——经典降维算法与框架综述_数据降维方法综述论文
赞
踩
目录
综述
在模式识别和机器学习领域,为了避免 "维度灾难",寻找高维数据的低维表示是一项基本任务。在过去的几十年里,大量的算法--有监督的或无监督的;来自统计学或几何学理论的--已经被设计出来,为降维问题提供不同的解决方案。本文在大量相关研究论文的基础上,对机器学习中经典的降维算法和降维框架进行了回顾和总结,包括算法的原理、过程和优化问题的推导,以及观点的统一和框架的构建。还通过实验分析了不同降维方法和框架应用于不同数据集的实验结果,并通过统计分析回顾和说明了算法框架之间的联系和区别。
索引范围-降维,流形学习,子空间学习,框架。
一、介绍
在模式识别和机器学习领域,许多应用,如基于外观的图像识别和文档分类,都面临着高维度的问题,而 "维度灾难 "会导致各种问题,如计算效率低和实验结果差。寻找高维数据的低维表示是一项基本任务。
使用减少的特征,分类可以更快、更稳健。因此,大量的有监督和无监督(线性降维、流形学习、核方法等)的降维算法和源于统计学或几何学理论的降维框架,用于解决机器学习发展中的降维问题,其中每种降维算法的原理、切入点和优化目标不同,导致不同算法之间的优化问题和算法过程不同,增加了学习、理解和应用的难度,因此一些降维框架(图嵌入框架、半监督降维框架等)已经被提出来,在一个统一的视角和平台下解释一些降维算法。
本文将介绍机器学习中经典的降维算法和框架的原理并推导出优化问题,并将不同的降维算法和框架应用于实际问题(以人脸识别为例),并结合统计和理论分析,对不同的降维方法和框架在不同的数据集上进行多维度的比较,并在分析实验现象和结果的基础上给出合理的实验结论。
本论文的其余部分结构如下。第2节介绍了各种经典降维算法的基本思路和优化问题的推导。第3节总结了经典降维算法的不足之处,并针对相应的不足之处提出了一种最优的降维方法。第四节,本文以图嵌入框架和半监督降维框架为例,介绍了降维框架的提出和构建方法。在第5节中,我们通过降维算法和框架在实验中的应用以及对实验结果的统计分析,说明了算法和框架之间的联系和区别。最后,我们在第6节中得出结论。
二、 降维算法回顾
在过去的几十年里,为了解决 "维度灾难 "的问题,很多降维算法都被提出来用于降维任务。尽管这些算法的动机、原理、切入点和优化目标都不一样,但它们的目标是相似的,即得出低维表示并促进后续分类任务的进行。
对于一般的分类问题,用于模型训练的样本集表示为矩阵X = [x1 , x2 , ..., xN], xi ∈ ℝm,其中N是样本数,m是特征维度(m维)。对于监督学习问题,假设样本xi的类标签为ci∈{1,2,...,Nc},其中Nc是类的数量。我们还让πc和nc分别表示属于第c类的样本的索引集和数量。降维的基本任务是找到一个映射函数F : x → y:将x∈ℝm转换为所需的低维表示y∈ℝd,其中,m >> d,如公式(1)所示:
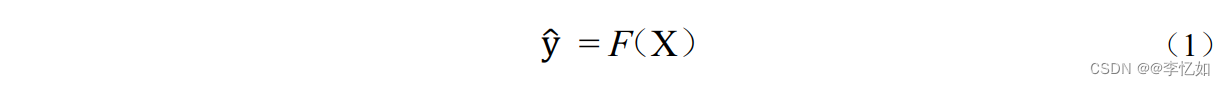
在不同的情况下,函数F可能是显性的或隐性的,线性的或非线性的。对于不同类型的数据,即向量、矩阵和本文后面介绍的一般张量,在图1中显示了一个直观的降维说明。在本节中,我们将从线性降维和流形学习的角度来推导一些经典降维算法的优化问题,并介绍相应的算法过程。

图1. 对不同形式的数据进行降维的说明。请注意,三阶张量数据是Gabor过滤的图像
1.KNN
在正式介绍降维算法之前,我们先介绍机器学习中最简单的算法之一:KNN。作为一种经典的分类算法,KNN在机器学习和模式识别领域的实际应用中经常与降维算法一起使用,这有助于更好地完成分类和识别等任务。
1.1 KNN核心思想
一个样本与数据集中的k个样本最为相似,如果这k个样本中的大多数属于某个类别,那么这个样本也属于这个类别。换句话说,这种方法只根据最近的一个或几个样本(k人为设定)的类别来决定要分类的样本的类别,KNN方法在类别决定中只与极少数的相邻样本有关,KNN算法的概念在图2中被直观地描述出来。

图2 KNN核心思想可视化样例
1.2 KNN算法流程
KNN的一般算法过程是用公式(2)或(3)计算给定的两个样本集X和Y的欧氏距离,将距离按升序排序,取前k个,并进行(加权)平均。
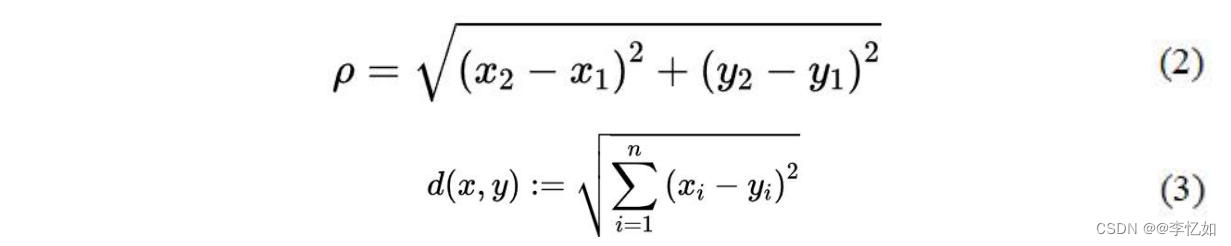
1.3 KNN算法优缺点
KNN算法优缺点如表1总结:
表1 KNN算法优缺点
| 优点 | 缺点 |
| 简单而有效 | 惰性学习 |
| 再训练的成本低 | 类别分类没有标准化 |
| 算法复杂度低 | 输出的可解释性不强 |
| 适用于类域交叉的样本 | 不均匀性 |
| 大样本的自动分类 | 计算量大 |
2.线性降维
线性降维,即用简单的线性方法对数据进行降维,在机器学习领域一般分为有监督算法和无监督算法,区别在于前者将数据的标签信息作为先验知识。本小节将以无监督的PCA和有监督的LDA这两种经典的降维算法为例,探讨线性降维的特点,分析其实验效果和优缺点。
(1)PCA
2.1.1 PCA简介
PCA(主成分分析)是一种主流的、简单的无监督的线性降维算法。它以 "重建误差最小化 "或 "散点最大化 "为目标,在低维空间中找到一个有效的投影轴,通过投影,将原始数据中相对重要的信息表达出来,从而达到降维的目的,PCA的算法概念直观地描绘在图3中:
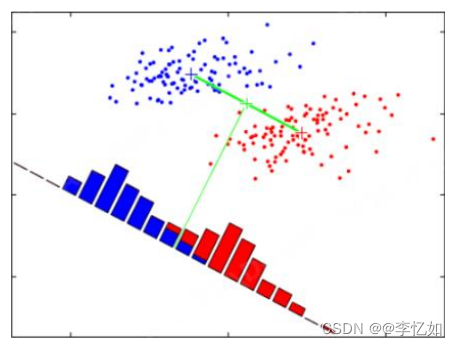
图3 PCA原理可视化
2.1.2 PCA优化问题与算法流程
根据PCA的核心关注点,考虑到整个数据集,原始样本点和基于投影的重构样本点之间的关系应该按照最近可重构性最小化,所以PCA的优化问题可以写成公式(4),其中W是正交基的集合,∑i x_i x_i^T是协方差矩阵。
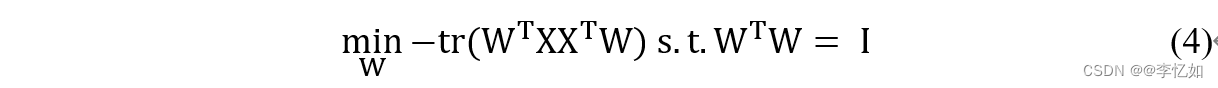
从最大可分性出发,可以得到PCA的另一种解释,即核心概念中提到的最大化投影样本点的散布,方程(5)就是这种解释下的PCA优化问题,其中∑i W^T x_i x_i^T W是样本点的方差。
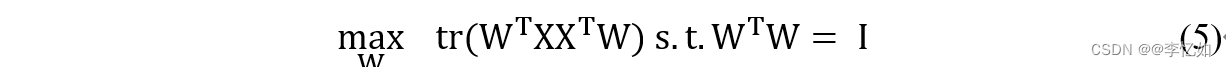
PCA优化问题的解决可以通过拉格朗日算子法和广义特征值分解得到。根据PCA的核心关注点和优化问题的解决,可以将PCA算法的步骤总结为表2:
表2 PCA算法流程
| 1.输入样本集的低维空间数d |
| 2.所有样本的集中化 |
| 3.计算样本XXT的协方差矩阵 |
| 4.对协方差矩阵进行特征值分解 |
| 5.取最大的d个特征值w1,w2...对应的特征向量 |
| 6.输出投影矩阵W = (w1,w2..., wd) |
PCA原理补充及其代码实践应用可见:
机器学习——PCA(主成分分析)与人脸识别_@李忆如的博客-CSDN博客_pca人脸识别
(2)LDA
2.2.1 LDA简介
LDA(线性判别分析)是一种主流的、简单的监督式线性降维算法。它以 "类内方差最小化,类间方差最大化 "为目标,找到可以优化分类的特征子空间,对数据进行投影,以达到降维的目的。图4直观地描述了LDA的算法概念。
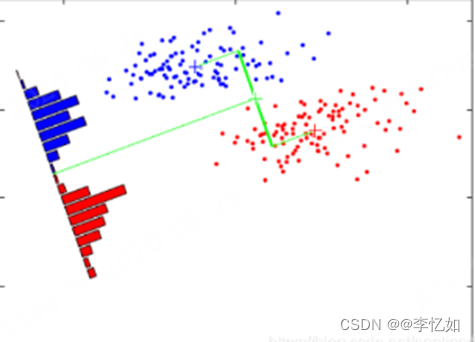
图4 LDA原理可视化
2.2.2 LDA优化问题与算法流程
由于LDA需要最小化类内方差和最大化类间方差,并发现最优分类的特征子空间,所以类内散射矩阵Sw和类间散射矩阵Sb定义在公式(6)和(7)中,LDA的优化问题可以改写为公式(8)(即Sb和Sw的 "广义瑞利商")。
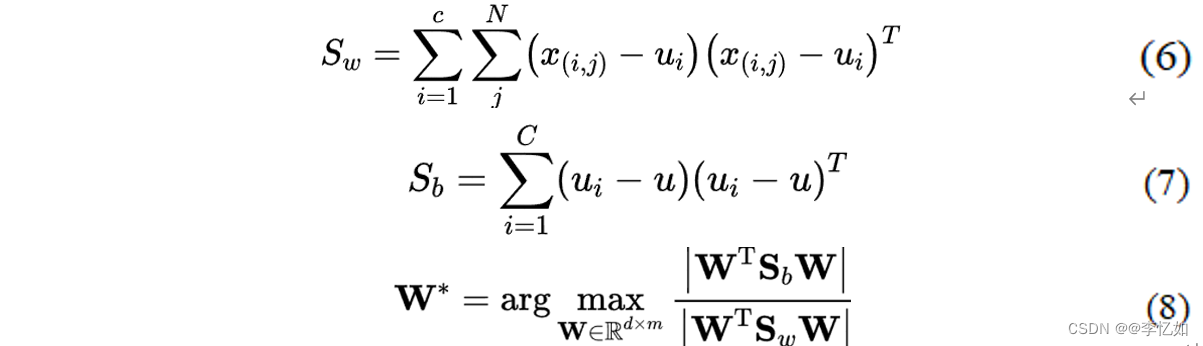
如何确定W?请注意,公式(8)中的分子分母是关于W的二次项,因此,(8)的解与W的长度无关,只与它的方向有关,不失为一个好办法,所以〖W^T S_ω W〗=1,那么公式(8)就等同于公式(9)。
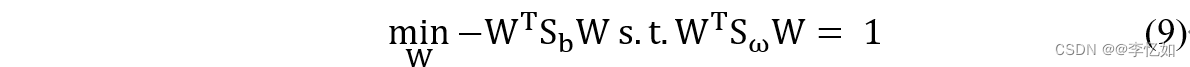
与PCA类似,LDA优化问题的解决可以通过拉格朗日算子法和广义特征值分解得到。根据LDA的核心关注点和优化问题的解决,可以将LDA算法的步骤总结为表3。
表3 LDA算法流程
| 1.输入具有低维空间数d的样本集 |
| 2.对数据集进行分类,并计算出每个类的均值 |
| 3.计算类间散点矩阵Sb和类内散点矩阵Sw |
| 4.构建目标函数Sω-1Sb并对其进行特征分解 |
| 5.取最大的d个特征值w1,w2...所对应的特征向量 |
| 6.输出投影矩阵W = (w1,w2..., wd) |
LDA原理补充及其代码实践应用可见:
机器学习——LDA(线性判别分析)与人脸识别_@李忆如的博客-CSDN博客_lda
3.流形学习
在机器学习和模式识别的实际应用中,直接使用线性降维往往是无效的,因为它没有考虑到数据样本在高维空间的分布和特点,所以提出了 "流形学习 "的概念。流形 "是指与欧氏空间局部同质的空间,而流形学习是一类借鉴拓扑流形概念的降维算法,即在高维空间中寻找低维流形并找到相应的嵌入映射,以更好地实现降维或数据可视化。图5通过一个简单的例子说明了流形学习的本质。
本节将以流形学习为例,介绍三种经典算法(MDS、Isomap和LLE)的原理、优化问题和算法过程,探讨流形学习的特点,并分析其实验效果和优缺点。
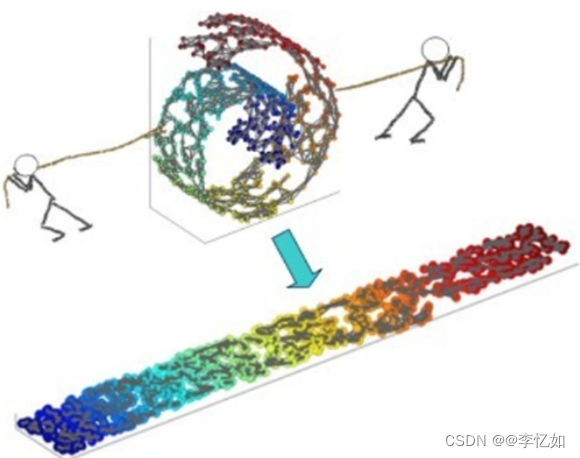
图5 流形学习原理可视化样例
(1)MDS
3.1.1 MDS简介
MDS(多维缩放)的核心概念是利用原始空间的距离矩阵D来计算减维样本的内积矩阵B,从而使减维的欧氏距离等于原始空间的距离。
3.1.2 MDS优化问题与算法流程
MDS的优化问题定义在公式(10)中,算法流程总结在表4中。
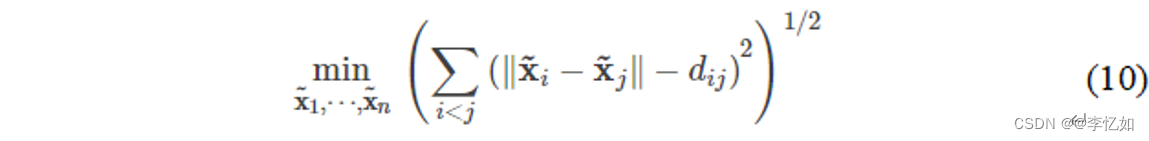
表4 MDS算法流程
| 1.输入距离矩阵D,低维空间数d |
| 2.根据相关公式计算出内积矩阵B |
| 3.对矩阵B做特征值分解 |
| 4.取由d个最大特征值组成的对角线矩阵A,V为其对应的特征向量矩阵。 |
| 5.输出矩阵VA1/2,每一行是一个样本的低维坐标 |
(2) Isomap
3.2.1 Isomap简介
Isomap(等距测绘)是一种主流的、简单的流形学习算法。从Isomap算法的角度来看,在高维空间中直接计算直线距离是不合适的,Isomap的核心理念是 "利用流形局部与欧氏空间同质的特点建立最近邻连接图",将计算距离的问题转化为计算最近邻连接图上两点间最短路径的问题。
3.2.2 Isomap算法流程
Isomap的原理与MDS相似,不同的是Isomap对距离矩阵做了另一种处理,其距离矩阵使用两点之间的最短距离,所以Isomap重建的距离矩阵D可以作为MDS使用,其他过程是一样的。
(3)LLE
3.3.1 LLE简介
与Isomap试图保持近邻样本之间的距离不同,LLE(局部线性嵌入)试图保持邻域之间的线性关系,如图6所示,样本点的坐标可以通过邻域样本坐标的线性组合来重建,而且这种线性关系的表达在低维空间仍然可以保持。

图6 LLE原理可视化
3.3.2 LLE优化问题与算法流程
LLE首先找到每个样本x_i的近邻子标集Q,然后计算线性重构的系数ω_i。因此,不难得出LLE的原始优化问题为公式(11):
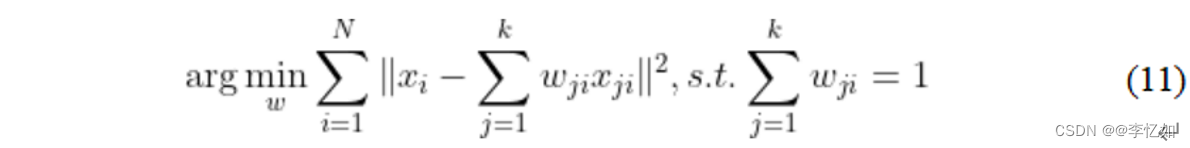
由于LLE在低维空间中保持重构系数ω_i不变,因此优化问题与低维空间中的z和高维空间中的x一一对应,其中,让M=(I-W)^T(I-W),优化问题可重写为公式(12):

与线性降维类似,LLE优化问题的解决可以通过拉格朗日算子法与广义特征值分解得到。根据LLE的核心概念和优化问题的解决,可以将LLE算法的步骤概括为表5:
表5 LLE算法流程
| 1.输入样本集D,最近的邻居参数k,低维空间的数量d |
| 2.确定每个样本点的k近邻,并找到相应的重建系数ωi |
| 3.根据M=(I-W)^T(I-W)找到M,对M进行特征值分解 |
| 4.返回M的d个最小的特征值所对应的特征向量 |
三、降维算法的优化
本节针对一些经典降维算法的不足之处,总结了一些优秀的优化算法或一些通用的优化方法。在以往的相关研究中,这些优化算法或方法已经被理论和实验证明优于原有的降维算法,在算法效率、算法流程、实验结果等部分有比较明显的优化。本节主要介绍原有算法的不足之处,一些优化降维算法(PCA、LDA)的优化思路和优化效果,以及一些通用的优化方法(正则化、核方法)。
1.2DPCA
1.1 PCA不足之处
通过分析PCA的优化问题推导和算法流程,我们不难发现许多不足之处,如表6所述:
表6 PCA不足
| 1.在高数据量的情况下,将矩阵转换为一维的计算量很大,会降低算法的效率。 |
| 2.PCA是无监督的,不利用样本信息作为先验知识 |
| 3.主成分特征维度的含义是模糊的,可解释性很差 |
| 4.对不符合高斯分布的数据效果不佳 |
1.2 2DPCA简介
2DPCA(Two-Dimensional PCA)是针对表6中PCA的第一个缺陷而优化的。2DPCA与PCA的区别在于,前者直接对矩阵进行操作,重新定义协方差矩阵,如公式(13),相当于去除图像的行向量或列向量的相关性,从而提高算法的效率,其他步骤和推导与经典PCA基本相同。
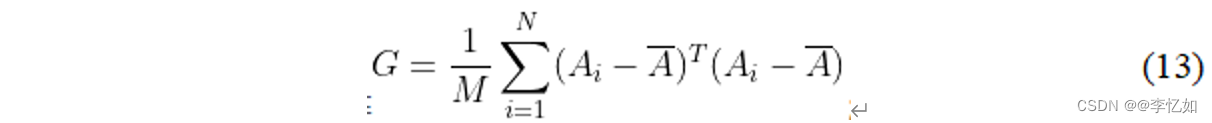
2.MMC
2.1 LDA不足之处
虽然LDA是机器学习和模式识别领域常用的有效监督算法,但通过分析LDA的优化问题推导和算法流程,还是发现了很多不足之处,如表7所述:
表7 LDA不足
| 1.有限投影轴问题(≤类的数量-1) |
| 2.小样本量问题 |
| 3.矩阵反演的计算成本高 |
| 4.不能更好地表征非线性问题 |
2.2 MMC简介
对于LDA来说,当数据量较小时,很难保证类内散射矩阵是非正交的,这就是表7中提到的小样本问题。为了克服LDA面临的小样本问题,研究人员提出了各种解决方案,如PCA+LDA算法、零空间LDA算法(NLDA)、正交LDA、完全LDA(CLDA)和Maxi- mum Margin Criterion(MMC)。在这些算法中,MMC是比较简单和著名的算法之一。
MMC以类间散射矩阵的迹与类内散射矩阵的迹之差作为判别标准,并在此基础上得到一个有效的投影轴,使不同类的样本具有更好的可分离性。因此,MMC不需要解决类内散射矩阵的逆矩阵。这样,MMC在理论上就避免了由于类内散射矩阵的奇异性而导致的LDA无法解决的问题,从而提高了算法的效率。如上所述,优化问题被重新定义为公式(14),其他步骤和推导与经典LDA基本相同。

3.正则化
3.1 分类(拟合)问题
回顾一下模型训练的过程,模型参数的训练实际上是一个不断迭代的过程,以找到一个适合数据集的方程。但是,在拟合过程中,根据模型拟合程度的不同,有三种拟合情况:欠拟合、拟合和过拟合。以分类问题为例,拟合问题的可视化效果如图7所示,而表8则分析了各种拟合情况的定义、原因和解决办法:

图7. 对分类问题的不同拟合情况的讨论
Tips:其中左图为欠拟合,中图为(适当)拟合,右图为过拟合。
表8 欠拟合和过拟合的分析
| 欠拟合 | 过拟合 | |
| 理由 | 1.训练样本数量少 2.模型复杂度低 3.在参数收敛前停止循环 | 1.数据噪音太大 2.特征太多 3.模型太复杂 |
| 解决方案 | 1.增加样本的数量 2.增加模型参数以提高模型的复杂性 3.增加循环次数 4.检查模型是否因为高学习率而无法收敛 | 1.清理数据 2.减少模型参数,降低模型的复杂性 3.增加惩罚因子,保留所有的特征,但减少参数的大小 |
3.2 正则化简介
通过3.3.1中对拟合问题的分析,可以加入一个正则化项来防止模型的过拟合。正则化是给成本函数增加一个约束条件,限制其高阶参数的大小不至于太大,从而提高模型效果的一种方法。对于不同的算法和模型,正则化项的类型也不同,包括L1正则化、L2正则化、半监督正则化等。在本小节中,我们以正则化LDA为例,分析正则化项如何优化算法和模型。
对于正则化LDA(RDA),实质上是在原目标函数中加入人为定义的参数(L2正则化项),以此来限制散点矩阵的大小,以达到更好的分离性和实验效果,RDA的优化函数可描述为公式(15),优化问题的推导和算法流程与LDA基本相同。

4.核方法
4.1 线性降维的不足
如二、2所述,线性降维一般是直接在有限投影轴的低维空间中寻找高维空间数据的最优子空间。然而,在机器学习和模式识别领域的实际任务中,数据往往很难完全满足完全的线性分布,此时线性降维的效果较差。除了上文中提到的流形学习外,另一种优化线性算法的方法是核方法。
4.2 核方法简介
核方法提出的动机是为了解决分类任务中的线性不可分性问题,其核心理念是通过特定的核函数ϕ:x→F将数据映射到高维的希尔伯特空间,然后在这个新的特征空间中执行算法,从而降低任务的难度,提高原算法的效果。在Hilbert空间中,可以用内积k(x_i ,x_j)=ϕ(x_i )·ϕ(x_j )来代替显式映射,一个简单的核方法的例子如图8所示:

图8 核方法的简单例子
对于机器学习和模式识别领域的不同任务,如果使用核方法进行优化,选择一个合适的核函数是至关重要的,如图9所示,几种经典的核函数具有很强的泛化性能,是常用的。

图9 几种经典的核函数
四、降维框架
经过第二节和第三节对各种降维算法及其优化的分析,我们不难发现,虽然不同的降维方法不断被提出和优化,但在原理上存在较大的差异,这就增加了学习、理解和应用的难度。针对这一问题,"框架思维 "已经被研究者们所研究,因此,降维框架的设计和构建已经成为机器学习和模式识别领域的一个热门研究方向。
本节将通过介绍两种经典的降维框架,即图嵌入和半监督降维框架,以及不同框架下统一的新的优化问题和各降维算法的新表达方式,并以降维框架为平台,开发新算法或优化现有算法,来介绍和分析降维框架的设计和构建方法。
1.图嵌入框架
为了统一不同动机的降维算法,提出了图嵌入降维框架,大多数降维算法都可以在这个共同的框架内重新表述,每个算法都可以被认为是直接的图嵌入或其线性/核/张量扩展,用于描述数据集的某些期望的统计或几何属性,同时揭示了降维方案的基本优点和缺点。此外,图形嵌入框架可以作为开发新的降维算法的通用平台。
1.1 图嵌入视角下的降维
与图1中描述的经典降维过程不同,从图嵌入的角度来看,降维的核心是构造一个本征图来描述数据中有价值的统计或几何特征,以及一个惩罚图来描述数据中需要抑制的统计或几何特征,然后通过图嵌入对应的图保全准则(目标函数)来实现数据的降维,如公式(16)。对于上一节提到的线性方法和核方法,以及没有提到的张量方法,都有相应的图嵌入版本,主要区别在于构建本征图和惩罚图的方式不同。

其中,W是相似度矩阵,每个元素衡量一对顶点的相似度。L是一个拉普拉斯矩阵,在图嵌入的角度新定义为公式(17)。 d是一个常数,B是一个约束矩阵,定义为避免目标函数的琐碎解。b通常是一个对角线矩阵,用于尺度归一化,也可能是一个拉普拉斯矩阵,用于惩罚图Gp。
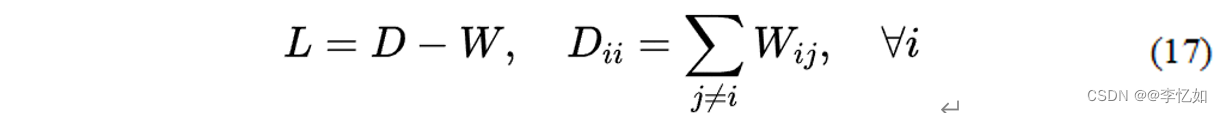
1.2 不同形式的图嵌入
为了适应不同类型的降维方法,图嵌入除了上文提到的直接图嵌入外,还有线性化、内核化和张量化三种不同的形式,不同的形式有不同但相似的保图准则(目标函数)。
图嵌入的线性化假定每个顶点的向量表示是由图顶点的原始特征向量表示线性投影出来的,图嵌入的内核化在线性图嵌入算法上应用内核技巧来处理非线性分布的数据。最后,在图嵌入的张量化中,原始顶点被编码为任意阶的一般张量,并应用多线性代数方法将直接图嵌入扩展到基于张量表示的多线性情况。其中,框架的统一表达如图10所示,表9中总结了经典降维算法在图嵌入角度的新表达。
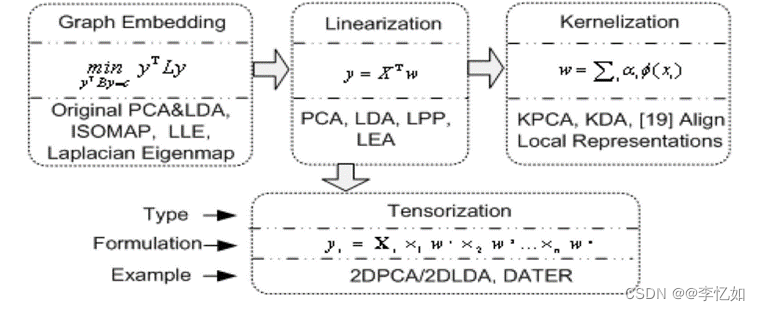
图10 图嵌入框架的统一表达
表9 流行降维算法的常见图嵌入视图

注意,D类型代表直接图嵌入,而L、K和T分别表示图嵌入的线性化、内核化和张量化。
1.3 图嵌入平台
除了统一具有不同动机和过程的各种降维算法外,图嵌入框架还可以作为开发新降维算法的通用平台。下面以图嵌入平台开发MFA(边际费雪分析)为例。
为了克服LDA在处理非高斯分布数据时,不同类的可分离性不能很好地用类间散布来描述,从而影响实验结果的情况,MFA应运而生。MFA是基于图保留准则开发的算法,其核心是利用图嵌入平台设计一个表征类内紧凑性的内在图和一个表征类间分离性的惩罚图,MFA的具体构造如图11所示,算法流程如表10所述:
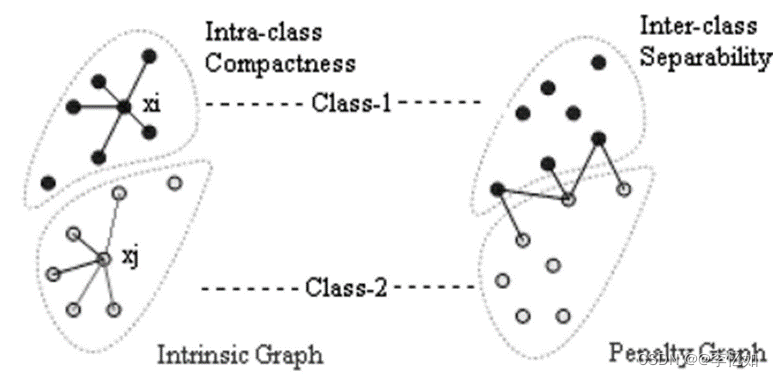
图11. MFA的本征图和惩罚图的相邻性
MFA算法流程
| 1.使用PCA的预测数据 |
| 2.构建类内紧凑性图和类间可分离性图 |
| 3.应用MFA线性化图保全准则并解决 |
| 4.输出投影矩阵 |
2.半监督降维框架
上文提到的图嵌入降维框架从线性、核化和张量的角度统一了不同类型的降维方法,并为开发新算法提供了一个平台。而半监督降维框架顾名思义,从监督/非监督的角度统一了不同的降维方法,并提出了相应算法的半监督版本及其核化。
半监督方法是指利用部分标记数据的标记信息,通过标记数据和未标记数据的组合来表示每个探测向量。它有效地避免了监督方法不使用数据的标签信息、效果普遍较差的缺点,也节省了监督学习需要标记所有数据的时间和精力。该框架的核心是基于正则判别分析和正则最小二乘法之间的关系,它可以在保留局部流结构的情况下判别多类子流形式。接下来我们通过介绍方程(18)中二元分类情况下LS的正则化框架来介绍半监督的降维框架。
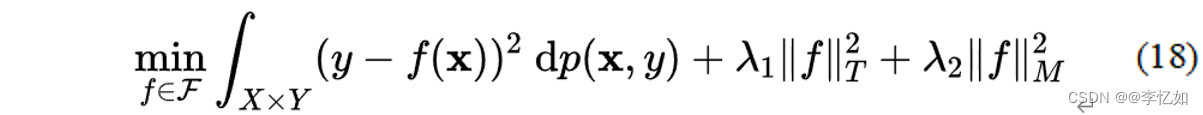
其中,函数由一组冗余基表示(本质上是原始优化问题),可应用于欧几里得空间和再生希尔伯特空间。‖f‖_T^2是函数空间的Tikhonov正则化项(L2),‖f‖_M^2是基于流形分析的正则化项(半监督正则化项)。
在半监督降维框架中,最重要的是半监督正则化的推导和解决。为了在其中同时使用有标签和无标签的信息,邻接矩阵M和归一化拉普拉斯图L被用来定义加权图。如图12所示,||f||_M^2被导出并求解。
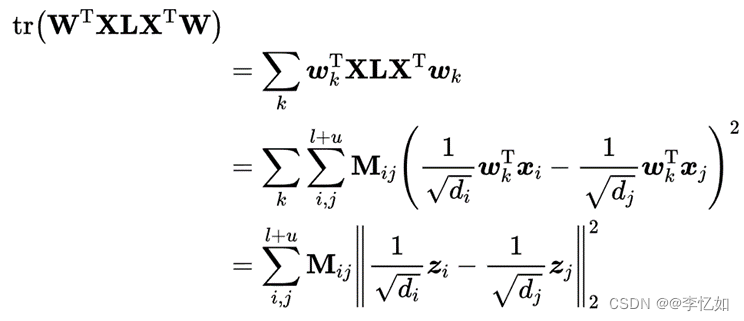
图12. 半监督正则化项的推导
构造出x后,可以通过将其加入到原来的降维算法的目标函数中来解决,算法过程基本相同。
五、实验
在本节中,我们将把前面提到的降维算法和降维框架应用到机器学习和模式识别领域的一个真实任务中(以人脸识别为例),通过对实验结果的统计分析,说明不同降维算法和框架之间的联系和区别,以及对其算法效果的对比。
在这个实验中,我们使用了以下人脸数据集,三个数据集的典型人脸如图13所示。
AT&T人脸数据。有40个不同的个体,每个个体有10个主题。每个人脸图像被调整为56 x 46像素,有256个灰度等级。这些图像是在不同时间拍摄的,改变了灯光、面部表情和面部细节。
耶鲁大学(Yale)的人脸数据。这个数据集包含15个人的165张图像。每张脸的图像被调整为69 x 58像素,有256个灰度等级。这些图像是在更多的配置下拍摄的,即照明(中光、左光和右光)、面部表情(快乐、正常、悲伤、困倦、惊讶和眨眼)以及带或不带眼镜。
UMIST脸部数据。这组数据包含20个人的564张图像。每张脸部图像都被调整为112 x 92像素,有256个灰度等级。这些图像涵盖了从侧面到正面的一系列姿势。

图13. 人脸数据的例子。(a) AT&T的人脸例子;(b) 耶鲁的人脸例子;(c) UMIST的人脸例子
我们在上述三个数据集上测试了前文提到的降维算法及其优化和算法框架,实验中分别探讨了不同降维数、不同训练集和测试集比例、不同数据集对算法和框架的影响,实验结果列举并绘制如下。
其中,每个实验平均进行10次,以平均人脸识别率为结果,每次都进行交叉验证,以保证实验结果的准确性,然后通过几何统计和多维度比较,对实验结果进行分析并提出实验结论。
表11 不同训练集和测试集比例对降维方法的影响(AT&T)

请注意,括号内的数字是降维后效果最好的相应特征维度。对于PCA+LDA和PCA+MFA,第一个数字是PCA步骤中保留的能量百分比,对于KDA和KMFA,数字是内核参数序列号,对于DATER和TMFA,两个数字分别是降维后的行和列号。

图14 不同降维数对降维方法的影响(Yale)
表12 不同数据集对降维方法的影响
| AT&T | Yale | UMIST | |
| PCA | 89.85% | 77.81% | 87.81% |
| LDA | 90.88% | 90.24% | 90.18% |
| LLE | 90.11% | 89.78% | 90.56% |
| 2DPCA | 90.88% | 86.8% | 90.24% |
| MMC | 91.44% | 90.87% | 92.71% |
| MFA | 96.0% | 94.8% | 95.2% |
| SSLDA | 92.66% | 93.02% | 93.17% |
根据表11、图14和表12中不同因素对不同降维算法和框架的影响分析,可以得出以下几个结论:
(1)对于不同的降维算法,随着训练集与测试集比例的增加,算法可以获得更多的信息,实验效果(人脸识别率)也相应提高。
(2)对于不同的降维算法,随着降维次数的增加,算法可以保留更多的信息(有上限),实验效果(人脸识别率)先上升后稳定或逐渐波动。
(3)对于不同的降维算法,在不同的数据集下,效果差异波动区间比较大,在不同的降维问题上要结合多种因素来考虑使用降维方法和框架。
(4) 总的来说,对于大多数降维的数据集,优化后的算法都显示出相对于原始算法的优越性,并且在实验中验证了框架算法的正确性。
六、结论
在本文中,我们总结了机器学习和模式识别领域的经典降维算法和降维框架。降维算法部分包括各种经典算法的原理、公式推导和算法过程,以及它们在线性降维、流动学习、核方法(监督、无监督和半监督)中的优化算法。
降维框架部分将各经典降维方法分别统一在图嵌入框架和半监督框架这两个经典降维框架的视角下,并以此探讨和分析了降维框架的设计和构建方法,分析了以降维框架为平台开发新算法的步骤。
此外,通过降维算法和降维框架在不同任务的数据集实验中的应用以及实验结果的统计分析比较,说明了各算法和框架之间的联系和区别。
七、主要参考文献
1.周志华《机器学习》
[1] Yangqiu Song, “A unified framework for semi-supervised dimensionality reduction”, Jan 2008.
[2] X. He, S. Yan, Y. Hu, P. Niyogi, H. Zhang, Face recognition using laplacianfaces, IEEE Trans. Pattern Anal. Mach. Intell. 27 (3) (2005) 328–340.
[3] J. Ye, Least squares linear discriminant analysis, in: International Conference on Machine Learning, 2007, pp. 1087–1093.
[4] W. Du, K. Inoue, K. Urahama, Dimensionality reduction for semisupervised face recognition, in: Proceedings of the Fuzzy Systems and Knowledge Discovery, 2005, pp. 1–10.
[5] D. Zhang, Z.-H. Zhou, S. Chen, Semi-supervised dimensionality reduction, in: SIAM Conference on Data Mining (SDM), 2007.
[6] P.N. Belhumeur, J.P. Hespanha, D.J. Kriegman, Fisherfaces: recognition using class specific linear projection, IEEE Trans. Pattern Anal. Mach. Intell. 19 (7) (1997) 711–720.
[7] A. Batur and M. Hayes, “Linear Subspaces for Illumination Robust Face Recognition,” Proc. IEEE Int’l Conf. Computer Vision and Pattern Recognition, vol. 2, pp. 296-301, Dec. 2001.
[8] I. Joliffe, Principal Component Analysis. Springer-Verlag, 1986.
[9] A.M. Martinez and A.C. Kak, “PCA versus LDA,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 23, no. 2, pp. 228-233, Feb. 2001.
[10] Shuicheng Yan, Member “Graph Embedding and Extensions: A General Framework for Dimensionality Reduction, ”IEEE TRANSACTIONS ON PATTERN ANALYSIS AND MACHINE INTELLIGENCE, VOL. 29, NO. 1, JANUARY 2007
[11] K.-R. Mu¨ller, S. Mika, G. Ra¨tsch, K. Tsuda, and B. Scho¨lkopf, “An Introduction to Kernel-Based Learning Algorithms,” IEEE Trans. Neural Networks, vol. 12, no. 2, pp. 181-201, 2001.
[12] M.H. Yang, “Kernel Eigenfaces vs. Kernel Fisherfaces: Face Recognition Using Kernel Methods,” Proc. Fifth IEEE Int’l Conf. Automatic Face and Gesture Recognition, pp. 215-220, May 2002.
[13] P.N. Belhumeur, J.P. Hespanha, and D.J. Kriengman, “Eigenfaces vs. Fisherfaces: Recognition Using Class Specific Linear Projection,” IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 19, no. 7, pp. 711-720, July 1997.
[14] H. Yu and J. Yang, “A Direct LDA Algorithm for HighDimensional Data—With Application to Face Recognition,”Pattern Recognition, vol. 34, no. 10, pp. 2067-2070, 2001.
[15] L. Sirovich and M. Kirby, “Low-dimensional procedure for the characterization of human faces,” J. Opt. Soc. America A Opt. Image Sci. Vis., vol. 4, no. 3, pp. 519–524, 1987.
[16] M. Turk and A. Pentland, “Eigenfaces for recognition,” J. Cogn. Neurosci., vol. 3, no. 1, pp. 71–86, Jan. 1991.
[17] W.-H. Yang and D.-Q. Dai, “Two-dimensional maximum margin feature extraction for face recognition,” IEEE Trans. Syst., Man, Cybern. B,Cybern., vol. 39, no. 4, pp. 1002–1012, Aug. 2009.
[18] A.J. Smola, S. Mika, B. Scho¨lkopf, and R.C. Williamson, “Regularized Principal Manifolds,” J. Machine Learning Research, vol. 1, pp. 179-209, June 2001.
[19] M. Belkin and P. Niyogi, “Laplacian Eigenmaps for Dimensionality Reduction and Data Representation,” Neural Computation, vol. 15, no. 6, pp. 1373-1396, 2003.
[20] H.S. Seung and D.D. Lee, “The Manifold Ways of Perception,”Science, vol. 290, pp. 2268-2269, Dec. 2000.
[21] T. Lin, H. Zha, and S. Lee, “Riemannian Manifold Learning forNonlinear Dimensionality Reduction,” Proc. Ninth European Conf. Computer Vision, pp. 44-55, May 2006.
[22] M. Balasubramanian, E.L. Schwartz, J.B. Tenenbaum, V. de Silva, and J.C. Langford, “The Isomap Algorithm and Topological Stability,” Science, vol. 295, p. 7a, Jan. 2002.
[23] F.S. Samaria, A.C. Harter, Parameterisation of a stochastic model for human face identification, in: IEEE Workshop on Applications of Computer Vision, 1994, pp. 138–142.
[24] A. Georghiades, P. Belhumeur, D. Kriegman, From few to many: Illumination cone models for face recognition under variable lighting and pose, IEEE Trans. Pattern Anal. Mach. Intell. 23 (6) (2001) 643–660.
[25] D. Graham, N. Allinson, Characterizing virtual eigensignatures for general purpose face recognition, Face Recognition: From Theory to Appl. 163 (1998) 446–456.


