一元线性回归（Python）_python一元线性回归

（补充）矩阵的转置

        矩阵的转置是指交换矩阵的行和列，行变成列，列变成行

        对于[ 123210 ].T  =  [122130]

1.线性回归的概念

        监督学习->回归问题->线性回归

        用于预测输入变量和输出变量之间的关系，特别是当输入变量的值发生变化时，输出变量的值随之发生的变化。回归模型正是表示从输入变量到输出变量之间映射的函数，回归问题的学习等价于函数拟合     

2.线性回归的分类

        如果研究的线性代数只包含一个自变量和一个因变量，且二者的关系可以通过一条直线近似的刻画时，这种回归就称为一元线性回归。

        如果回归分析中涉及到两个及以上的自变量，且自变量与因变量是线性关系，就称为多元线性回归。

一元线性回归模型的拟合：

最常用的有最小二乘法和梯度下降算法，下面我们分别讲讲最小二乘法和梯度下降算法，主要讲解梯度下降算法。

3.最小二乘法

       求出一些模型中未知参数（例如：y=a*x+b中的参数a、b）使得样本点和拟合线的总误差（距离）最小最直观的感受如下图

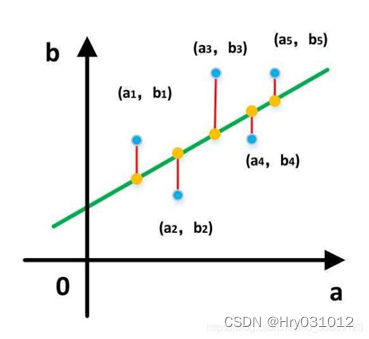
        而这个误差（距离）可以直接相减，但是直接相减会有正有负，相互抵消了，所以就用差的平方

        推导过程：

        

   最小二乘法代码 ：

	import numpy as np
	from matplotlib import pylab as pl
	#Defining training data
	x = np.array([1,3,2,1,3])
	y = np.array([14,24,18,17,27])
	# The regression equation takes the function
	def fit(x,y):
	    if len(x) != len(y):
	        return
	    numerator = 0.0
	    denominator = 0.0
	    x_mean = np.mean(x)
	    y_mean = np.mean(y)
	    for i in range(len(x)):
	        numerator += (x[i]-x_mean)*(y[i]-y_mean)
	        denominator += np.square((x[i]-x_mean))
	    print('numerator:',numerator,'denominator:',denominator)
	    b0 = numerator/denominator
	    b1 = y_mean - b0*x_mean
	    return b0,b1
	# Define prediction function
	def predit(x,b0,b1):
	    return b0*x + b1
	# Find the regression equation
	b0,b1 = fit(x,y)
	print('Line is:y = %2.0fx + %2.0f'%(b0,b1))
	# prediction
	x_test = np.array([0.5,1.5,2.5,3,4])
	y_test = np.zeros((1,len(x_test)))
	for i in range(len(x_test)):
	    y_test[0][i] = predit(x_test[i],b0,b1)
	# Drawing figure
	xx = np.linspace(0, 5)
	yy = b0*xx + b1
	pl.plot(xx,yy,'k-')
	pl.scatter(x,y,cmap=pl.cm.Paired)
	pl.scatter(x_test,y_test[0],cmap=pl.cm.Paired)
	pl.show()

结果分析：

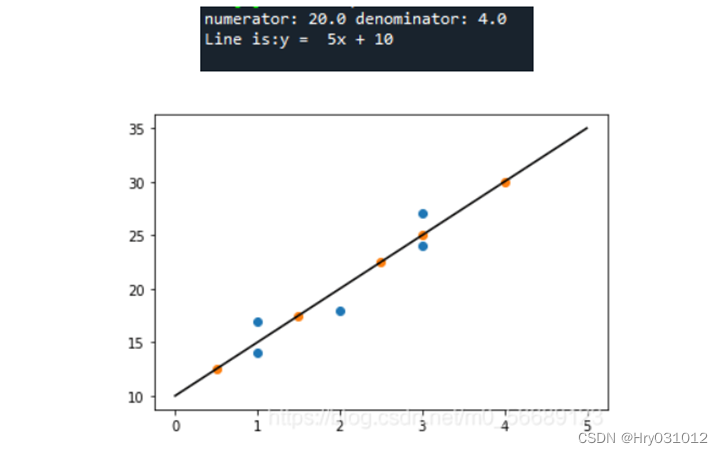
4.梯度下降算法

1目标/损失函数的构建

损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越好， 通常模型的性能越好。不同的模型用的损失函数一般也不一样。在应用中，通常通过最小化损失函数求解和评估模型。

求解最佳参数，需要一个标准来对结果进行衡量，为此我们需要定量化一 个目标函数式，使得计算机可以在求解过程中不断地优化。

针对任何模型求解问题，都是最终都是可以得到一组预测值 y^，对比已有的真实值y ，数据行数为n ，可以将损失函数定义如下：

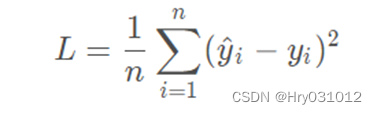
即预测值与真实值之间的平均的平方距离，统计中一般称其为MAE(mean square error)均方误差。把之前的函数式代入损失函数，并且将需要求解 的参数w和b看做是函数L的自变量，可得：

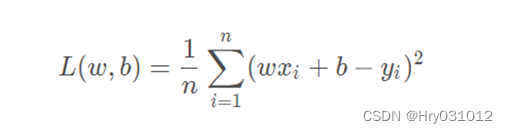
现在的任务是求解最小化L时w 和b 的值，

即核心目标优化式为：

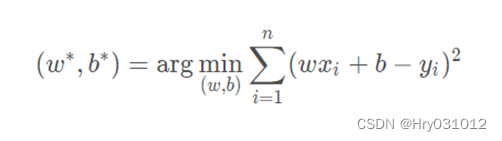
2 梯度下降三兄弟（BGD，SGD， MBGD）

我们在用梯度下降算法解决线性回归问题时需要采用数据集

现在有三种不同的采用方式，因此也产生了三种不同的梯度下降算法

下面涉及到数据集名词，可结合本篇内容三理解

2.1 批量梯度下降法（Batch Gradient Descent）

批量梯度下降法每次都使用训练集中的所有样本更新参数。它得到的是一 个全局最优解，但是每迭代一步，都要用到训练集所有的数据，如果m很 大，那么迭代速度就会变得很慢。 优点：可以得出全局最优解。 缺点：样本数据集大时，训练速度慢

2.2 随机梯度下降法（Stochastic Gradient Descent）

随机梯度下降法每次更新都从样本随机选择1组数据，因此随机梯度下降比 批量梯度下降在计算量上会大大减少。SGD有一个缺点是，其噪音较BGD 要多，使得SGD并不是每次迭代都向着整体最优化方向。而且SGD因为每 次都是使用一个样本进行迭代，因此最终求得的最优解往往不是全局最优 解，而只是局部最优解。但是大的整体的方向是向全局最优解的，最终的 结果往往是在全局最优解附近。 优点：训练速度较快。 缺点：过程杂乱，准确度下降。

2.3小批量梯度下降法（Mini-batch Gradient Descent）

小批量梯度下降法对包含n个样本的数据集进行计算。综合了上述两种方 法，既保证了训练速度快，又保证了准确度。

3 梯度下降法的一般步骤

假设函数：y = f ( x 1 , x 2 , x 3 . . . . x n )  只有一个极小点。

初始给定参数为X 0 = ( x 1 0 , x 2 0 , x 3 0.... x n 0 ) 。

从这个点如何搜索才能找到 原函数的极小值点?

方法：

①首先设定一个较小的正数 α , ε;

②求当前位置出处的各个偏导数：

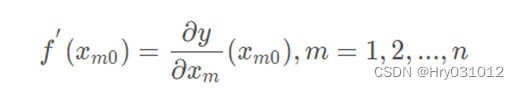
③修改当前函数的参数值，公式如下

 

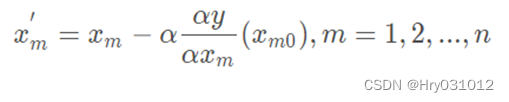
④如果参数变化量小于 ，退出；否则返回第2步。

 4 一元线性回归函数推导过程

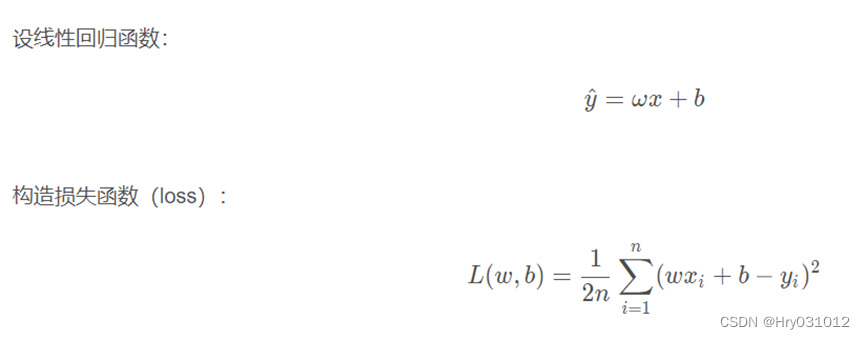
思路：通过梯度下降法不断更新 和 ，当损失函数的值特别小时，就得到
了我们最终的函数模型。
过程：、

5(实例)波士顿房价预测

房屋价格与面积（数据在下面表格中）：

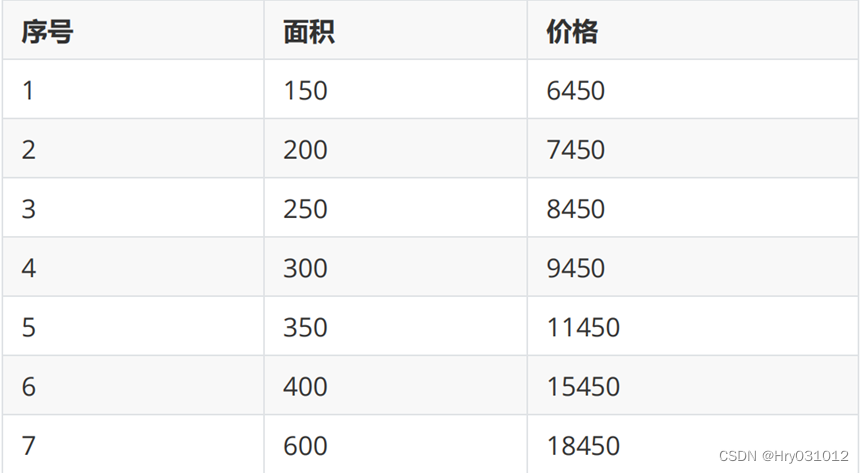
使用梯度下降求解线性回归（求 Θ1，Θ0）

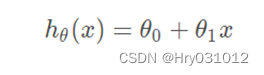
Python代码：

	#房屋价格与面积
	#序号：1     2    3    4     5     6     7
	#面积：150  200  250  300   350   400   600  
	#价格：6450 7450 8450 9450 11450 15450 18450 
	import matplotlib.pyplot as plt
	import matplotlib
	from math import pow
	import random
	x0 = [150,200,250,300,350,400,600]
	y0 = [6450,7450,8450,9450,11450,15450,18450]
	#为了方便计算，将所有数据缩小 100 倍
	x = [1.50,2.00,2.50,3.00,3.50,4.00,6.00]
	y = [64.50,74.50,84.50,94.50,114.50,154.50,184.50]
	#线性回归函数为 y=theta0+theta1*x
	#损失函数 J (θ)=(1/(2*m))*pow((theta0+theta1*x[i]-y[i]),2)
	#参数定义
	theta0 = 0.1#对 theata0 赋值
	theta1 = 0.1#对 theata1 赋值
	alpha = 0.1#学习率
	m = len(x)
	count0 = 0
	theta0_list = []
	theta1_list = []
	#1.使用批量梯度下降法
	for num in range(10000):
	    count0 += 1
	    diss = 0   #误差
	    deriv0 = 0 #对 theata0 导数
	    deriv1 = 0 #对 theata1 导数
	    #求导
	    for i in range(m):
	        deriv0 += (theta0+theta1*x[i]-y[i])/m#对每一项测试数据求导再求和取平均值
	        deriv1 += ((theta0+theta1*x[i]-y[i])/m)*x[i]
	    #更新 theta0 和 theta1
	    theta0 = theta0 - alpha*deriv0 
	    theta1 = theta1 - alpha*deriv1
	    #求损失函数 J (θ)
	    for i in range(m):
	        diss = diss + (1/(2*m))*pow((theta0+theta1*x[i]-y[i]),2)
	            
	    theta0_list.append(theta0*100)
	    theta1_list.append(theta1)
	    #如果误差已经很小，则退出循环
	    if diss <= 0.001:
	        break
	theta0 = theta0*100#前面所有数据缩小了 100 倍，所以求出的 theta0 需要放大 100 倍，theta1 不用变
	#2.使用随机梯度下降法
	theta2 = 0.1#对 theata2 赋值
	theta3 = 0.1#对 theata3 赋值
	count1 = 0
	theta2_list = []
	theta3_list = []
	for num in range(10000):
	    count1 += 1
	    diss = 0   #误差
	    deriv2 = 0 #对 theata2 导数
	    deriv3 = 0 #对 theata3 导数
	    #求导
	    for i in range(m):
	        deriv2 += (theta2+theta3*x[i]-y[i])/m
	        deriv3 += ((theta2+theta3*x[i]-y[i])/m)*x[i]
	    #更新 theta0 和 theta1
	    for i in range(m):
	        theta2 = theta2 - alpha*((theta2+theta3*x[i]-y[i])/m) 
	        theta3 = theta3 - alpha*((theta2+theta3*x[i]-y[i])/m)*x[i]
	    #求损失函数 J (θ)
	    rand_i = random.randrange(0,m)
	    diss = diss + (1/(2*m))*pow((theta2+theta3*x[rand_i]-y[rand_i]),2)
	    
	    theta2_list.append(theta2*100)
	    theta3_list.append(theta3)
	    #如果误差已经很小，则退出循环
	    if diss <= 0.001:
	        break
	theta2 = theta2*100
	print("批量梯度下降最终得到theta0={}，theta1={}".format(theta0,theta1))
	print("           得到的回归函数是：y={}+{}*x".format(theta0,theta1))
	print("随机梯度下降最终得到theta0={}，theta1={}".format(theta2,theta3))
	print("           得到的回归函数是：y={}+{}*x".format(theta2,theta3))
	#画原始数据图和函数图
	matplotlib.rcParams['font.sans-serif'] = ['SimHei']
	plt.plot(x0,y0,'bo',label='数据',color='black')
	plt.plot(x0,[theta0+theta1*x for x in x0],label='批量梯度下降',color='red')
	plt.plot(x0,[theta2+theta3*x for x in x0],label='随机梯度下降',color='blue')
	plt.xlabel('x（面积）')
	plt.ylabel('y（价格）')
	plt.legend()
	plt.show()
	plt.scatter(range(count0),theta0_list,s=1)
	plt.scatter(range(count0),theta1_list,s=1)
	plt.xlabel('上方为theta0，下方为theta1')
	plt.show()
	plt.scatter(range(count1),theta2_list,s=3)
	plt.scatter(range(count1),theta3_list,s=3)
	plt.xlabel('上方为theta0，下方为theta1')
	plt.show()

 结果显示：

 

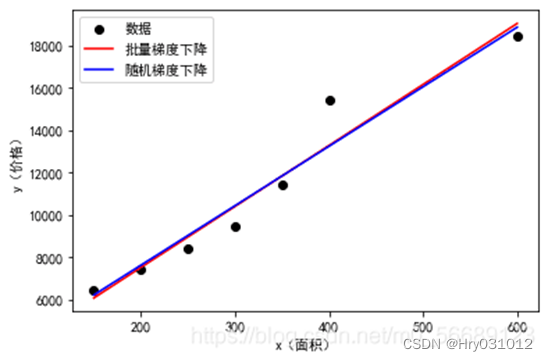
批量梯度下降：

 

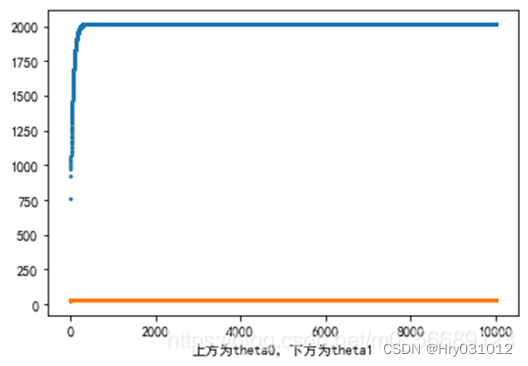
随机梯度下降：

 

 我的笔记：