$\begin{bmatrix} a11 &a12 \\ a21 & a22 \end{bmatrix} + \begin{bmatrix} c11 & a12 \\ c21 & a22 \end{bmatrix} = \begin{bmatrix} a11+c11 &a12+a12 \\ a21+c21 & a22+a22 \end{bmatrix}$

$\begin{vmatrix} a11 & a12\\ a21 & a22 \end{vmatrix} + \begin{vmatrix} c11 & a12\\ c21 & a22 \end{vmatrix} = \begin{vmatrix} a11+c11 & a12\\ a21+c21 & a22 \end{vmatrix}$

3.2 减法不同

减法的差别，参考加法

3.3 标量乘法/数乘

3.3.1 标准的数乘对比

矩阵的标量乘法 λ*A=λ*每个元素，*A*B=A*λ*B
行列式的标量乘法，λ*|A|=λ*某1行/列

$b*\begin{bmatrix} a11 & a12\\ a21 & a22 \end{bmatrix} = \begin{bmatrix} b*a11 & b*a12\\ b*a21 & b*a22 \end{bmatrix}$

$b* \begin{vmatrix} a11 & a12\\ a21 & a22 \end{vmatrix} = \begin{vmatrix} b*a11 & a12\\ b*a21 & a22 \end{vmatrix} = \begin{vmatrix} b*a11 & b*a12\\ a21 & a22 \end{vmatrix}$

3.3.2 数乘的扩展

矩阵的数乘

矩阵的标量乘法始终如此（λ*A）=λ*（A）

行列式得数乘扩展

行列式的标量乘法，|λ*A|=λ^n*|A| ，其中n是满秩矩阵A的秩/维度
行列数乘法： |Ann*Bnn| =|Ann|*|Bnn|
行列数乘法： |2Ann*Bnn| =|2Ann|*|Bnn| =2^n*|Ann|*|Bnn|

里面是矩阵的数乘，矩阵（假设是方阵）的数乘是每行每列都*λ
而行列式的数乘是某1行/列*λ
因此每行的λ 都可以提出来，因此是n 个λ 相乘=λ^n

3.4 乘法

矩阵乘法

矩阵乘法：点乘
矩阵乘法：叉乘

行列式应该只有标量乘法，没有其他乘法吧?

4 初等线性变换的不同

线性变换包含，行的线性变换和列的线性变换

行的线性变换

行之间，交换
某行乘以倍数
某行乘倍数+到其他行

列的线性变换

列之间，交换
某列乘以倍数
某列乘倍数+到其他列

4.1 对矩阵进行线性变换

无论是线性行变换，还是线性列变换，矩阵还是等价得

交换某行/列
倍数
倍加

矩阵进行线性变换后的结果

线性变换前后系统的特征值不变；
线性变换前后系统的传递函数矩阵不变；

4.2 对行列式进行线性变换

交换：如果交换行列式|A| 的任意两行/列，增加一个负号-
倍数：如果行列式|A| 某1行或列*λ，|A| 变成 λ*|A|
（如果行列式(对应方阵)每行每列都*λ，那么 A| 变成 λ^n*|A|）
倍加：如果行列式|A| 某1行或列*λ后，再加到另外某1行/列，|A| 不变还是=|A|
总结，只有进行倍加的线性变换之后，行列式才不变化

解释原因

因为行列式其实代表有向的面积比，所以交换行列式|A| 的任意两行/列，增加一个负号-
因为行列式的标量乘法 λ*|A|= 把行列式的某1行/列* λ，所以行列式|A| 某1行或列*λ，|A| 变成 λ*|A|

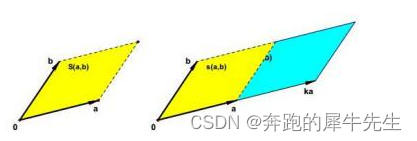
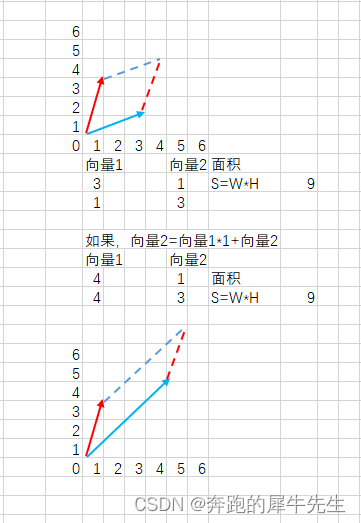
因为行列式其实代表有向的面积比，所以行列式|A| 某1行或列*λ后，再加到另外某1行/列，|A| 不变还是=|A|

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/菜鸟追梦旅行/article/detail/711473