- 1Cboard框架搭建及使用
- 26行代码 超级简单 语言情感分析 - 使用Python的vaderSentiment库实现
- 3Transformer_positionwiseffn
- 4局域网win10 主机之间相互共享文件的配置_局域网共享 最全 设置
- 5美丽新世界_2002 red hat 产品的两个系列是
- 6软件外包项目的管理
- 7小程序中使用微信同声传译插件实现语音识别、语音合成、文本翻译功能----语音识别(一)_小程序同声传译
- 8w8计算机主程序在哪里,Win8怎么打开运行窗口_Win8运行在哪里打开?-192路由网
- 9strncat函数使用时出现的bug_strncat函数常见报错
- 10Java基于微信小程序的校园跑腿系统的设计与实现_跑腿服务微信小程序开发实例
【算法设计与分析】1.排序算法性能分析_画出输入规模与消耗时间之间的曲线图
赞
踩
相关资源下载链接
要求pdf+报告word+pre ppt+cpp源代码大礼包
目录
2.不同排序算法在 20 个随机样本的平均运行时间与输入规模 n 的关系(如图12)
现在有 1 亿的数据,请选择合适的排序算法与数据结构,在有限的时间内完成进行排序。
写在前面的话
挺野蛮生长,之前半年打了c语言的题,还没打数据结构的题就直接上算法,只能说是梁静茹给我的勇气了。数据结构只是前几年浅浅过了概念,那时还未入行,虽然作为选修水课通宵搞通概念意外A+。。。(的确真水)。去年边学c边旁听了下,其实啥也也没听进入,emmm不管那么多感觉还能冲,直接上吧。为了拿个满分直接上台pre吧(纯纯被老师批斗也没事),在线忽略伪dalao。
虽然还一屁股的stm32悬于头上,但也没事整理整理这几个月的战绩吧,当复习了(其实是觉得这博客再荒废下去就废了。。。以后找工作难顶)。
还是觉得老师一句话还是有点道理的,这算法思维更重要。我作为个纯纯小白过来挑战算法,啥都没学过只能自己想写法子理解消化,求求平安过关别拉绩点~~~
概览
1. 选择排序、冒泡排序、合并排序、快速排序、插入排序算法原理
2. 不同排序算法时间效率的经验分析方法,验证理论分析与经验分析的一致性。
算法原理
排序问题要求我们按照升序排列给定列表中的数据项,目前为止,已有多种排序算法提出。本实验要求掌握选择排序、冒泡排序、合并排序、快速排序、插入排序算法原理,并进行代码实现。通过对大量样本的测试结果,统计不同排序算法的时间效率与输入规模的关系, 通过经验分析方法,展示不同排序算法的时间复杂度,并与理论分析的基本运算次数做比较, 验证理论分析结论的正确性。
选择排序(Selection sort)是一种简单直观的排序算法。它的工作原理是:第一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。
冒泡排序原理是临近的数字两两进行比较,按照从小到大或者从大到小的顺序进行交换,这样一趟过去后,最大或最小的数字被交换到了最后一位,然后再从头开始进行两两比较交换,直到倒数第二位时结束。
合并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。合并排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。合并排序也叫归并排序。
快速排序首先任意选取一个数据(通常选用数组的第一个数)作为关键数据,然后将所有比它小的数都放到它左边,所有比它大的数都放到它右边。
插入排序的基本思想是将一个记录插入到已经排好序的有序表中,从而一个新的、记录数增1的有序表。在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面有序表进行待插入位置查找,并进行移动。
排序算法及伪代码
选择排序
编程入门就冒泡和选择吧,这2个没啥好说的,实现简单逻辑粗暴(好记哈哈哈)。如果升序,选择排序就是不断挑出剩余最小放到最前面,有点像打牌时我们给牌排序(当然个人习惯这么排)。日常生活也有很多排序我们可以用这种方法。2趟循环实现,时间复杂度O()。
选择排序伪代码:
- SELECTION-SORT(A,n)
- for j = 1 to n - 1
- min = A[j]
- k = j
- //记录最小数的下标
- for i = j + 1 to n
- if A[i] < min
- min = A[i]
- k = i
- A[k] = A[j]
- A[j] = min
冒泡排序
原理见上。如果升序,剩余最大的数(泡)总会冒到最后,这个通过两两比较交换就可实现。
冒泡排序伪代码:
- BUBBLE-SORT(A,n)
- for j = 2 to n
- for i = 1 to n – j
- if A[j] > A[j+1]
- swap(A[j],A[j+1])
合并排序
脑洞小故事
我们可以想象成有一排人想按身高排序。队长收到需要排序的任务。但他觉得自己一个人独自完成这份工作负担是在太重了,时间效率也不高。同时他觉得自己的工作是领导队伍,具体工作应该是下分给下属完成。所以他将人员(包括他自己)从中间一分为二分为2个小队并任命2个小队长,让他们各自先排序下(分治),自己看着2个比较有序的部分还比较好把他们合并再排序。
而2个小队长怎么排序呢?不难想到他们完全可以用队长的管理方法,继续下分。巡而往复,直到分到每队只有1人那就用排啦,交上去让队长们合并进行排序,并不断上交,直到合并到全队都排好。
效率高吗?
听起来貌似把事情搞复杂了,相比之下选择算法就更像我们平时排序的法子,不香吗一下子就排好,不用弄得分分合合,搞得更像领导们为了降低自己的工作量把一部分任务丢给下边的人,这么多的交接工作难道不会造成更大的开支吗?
但其实对于电脑来说效率是很高的,因为电脑不像人那么聪明,用选择排序人是很容易一下子跳出剩余最值。但电脑就麻烦了,它只能一个一个比较,才挑出1个。下次又得遍历全部。想想就知道时间复杂度很高。所以对电脑来说合并排序虽然听起来复杂,但是是很聪明的,比较适合它,相当于把大问题分解小问题,这就是分治思维。
合并排序伪代码
刚才说了过程复杂了很多,而代码实现其实就是用指令对上述过程进行模拟。
- MERGE(A,left,right)
- mid = (left + right) / 2
- for i = left to mid and j = mid+1 to right
- if A[i] < A[j]
- temp[k++] = A[i++]
- else
- temp[k++] = A[j++]
- while i <= mid
- temp[k++] = A[i++]
- while j <= right
- temp[k++] = A[j++]
- while k >= 0
- A[--j] = temp[--k]
-
- MERGE-SORT(A,left,right)
- if left < right
- mid = (left + right) / 2
- MERGE-SORT(A,left,mid)
- //递归调用
- MERGE-SORT(A,mid+1,right)
- MERGE(A,n,left,right)
快速排序伪代码
我们可以先以某个标准把数分为大小2堆,对每堆继续分堆,分到最后就排好了。
快速排序伪代码
标准设为第一个数,降序,小的靠右放,大的靠左放。那么至左找到第一个不符合的小数,至右找到第一个不符合的大数,互相交换。直到2个逼到中间,中间就放标准数。
- PARTITION(A,low,high)
- pivot = A[low]
- //首元素做参考值并记录
- while low < high
- while low < right and A[high] >= pivot
- high = high+1
- //从右到左依次找比参考值大的数
- num[low] = num[high]
- while low < right and A[high] >= pivot
- low = low +1
- //从左到右依次找比参考值小的数
- num[high] = num[low]
- num[low] = pivot
- //中间处放参考值
- return low;
-
- QUICK-SORT(A,low,high)
- if left < right
- pivot = PARTITION(A,low,high)
- //分割函数整理分类并返回支点下标
- QUICK-SORT(A,low,pivot-1)
- QUICK-SORT(A,pivot+1,high)
插入排序
给牌排序除了上面说的选择排序的方法,我们还经常可能采取取牌插到已排好序的牌里。自然叫插入排序。
插入排序伪代码
- INSERT-SORT(A,n)
- for j = 1 to n
- key = A[j]
- //key为待插数
- i = j -1
- for i to 0 and A[i] > key
- A[i + 1] = A[i]
- A[i + 1] = key
测试
1.以待排序数组的大小 n=10000 为输入规模,固定 n,随机产生 20 组测试样本,统计不同排序算法在 20 个样本上的平均运行时间;n=20000, n=30000, n=40000, n=50000重复
以下莫得感情,可以跳过
(1)输入规模n=10000不同排序平均时间(如图6)
选择排序t1 = 0.1325s
冒泡排序t2 = 0.6901s
合并排序t3 = 0.0012s
快速排序t4 = 0.00085s
插入排序t5 = 0.0678s





图表 6 n=10000不同排序平均时间
(2)输入规模n=20000不同排序平均时间(如图7)
选择排序t1 = 0.41825s
冒泡排序t2 = 2.7229s
合并排序t3 = 0.0025s
快速排序t4 = 0.00175s
插入排序t5 = 0.25925s
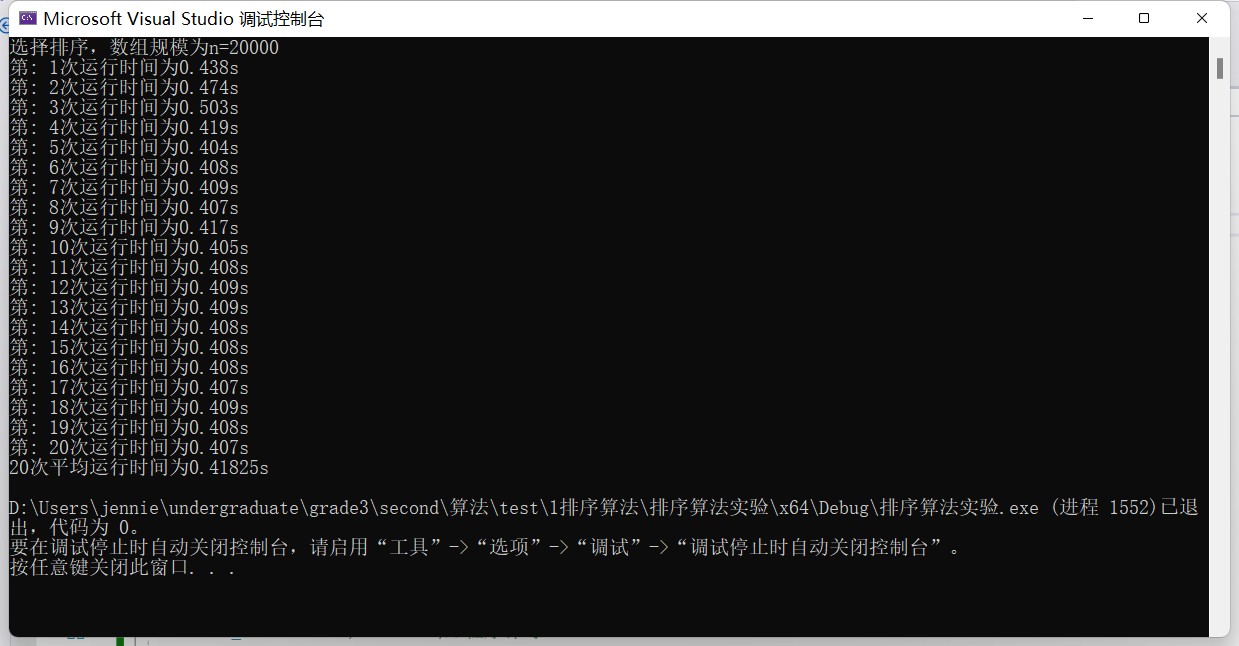



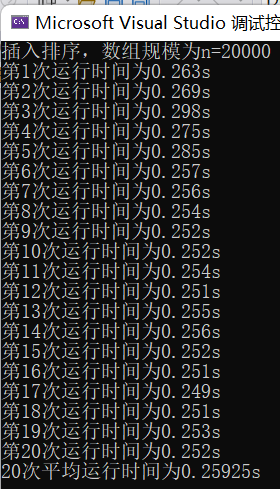
图表 7 n=20000不同排序平均时间
(3)输入规模n=30000不同排序平均时间(如图8)
选择排序t1 = 0.92415s
冒泡排序t2 = 6.136s
合并排序t3 = 0.004s
快速排序t4 = 0.00275s
插入排序t5 = 0.55435s
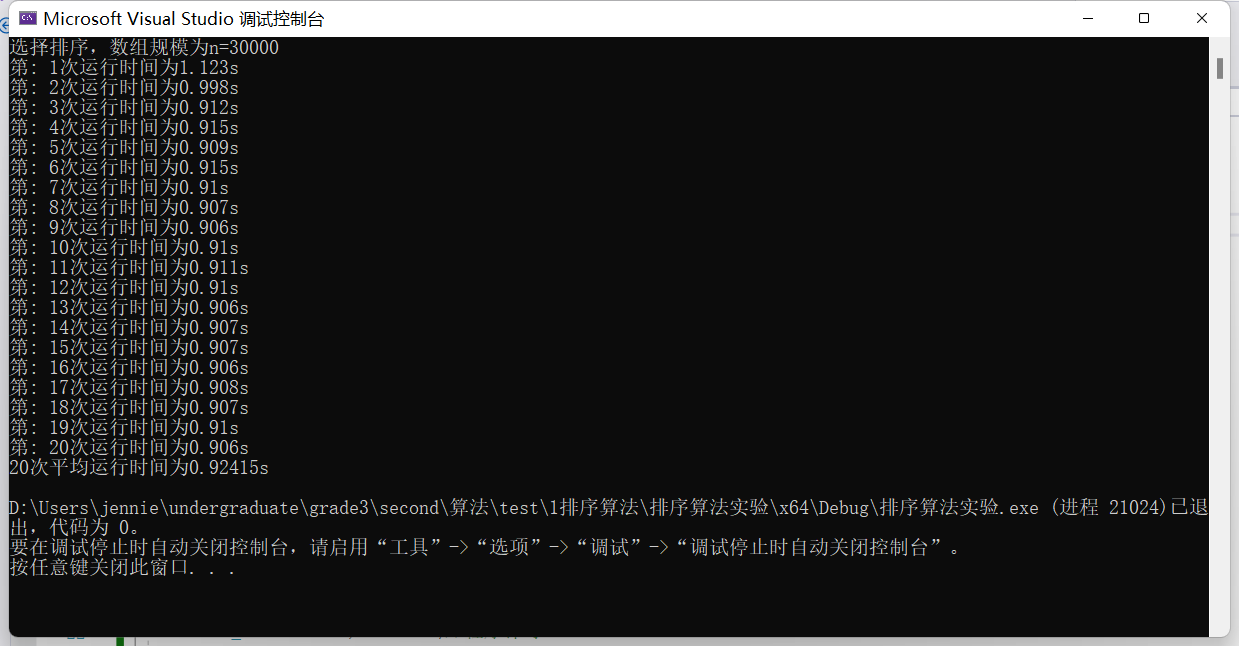


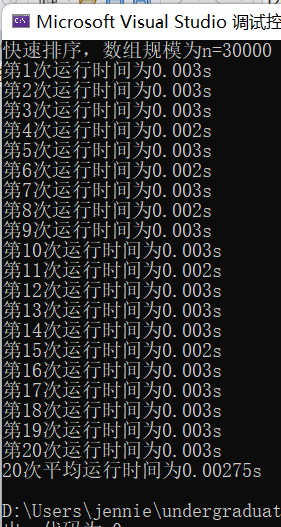

图表 8 n=30000不同排序平均时间
(4)输入规模n=40000不同排序平均时间(如图9)
选择排序t1 = 1.60885s
冒泡排序t2 = 10.9242s
合并排序t3 = 0.00545s
快速排序t4 = 0.00385s
插入排序t5 = 0.97275s
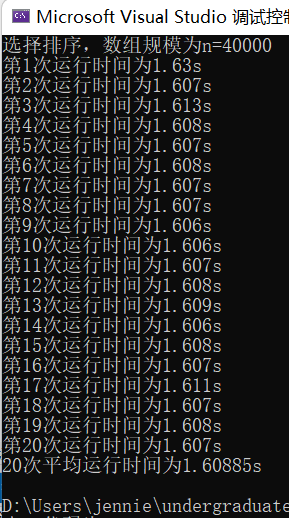
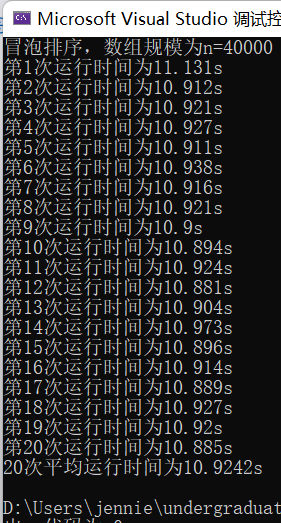
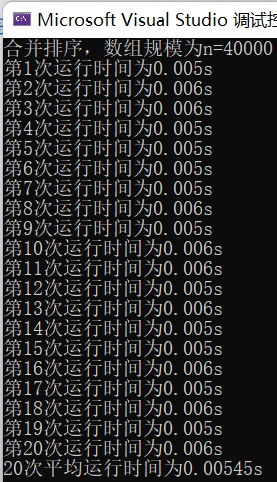

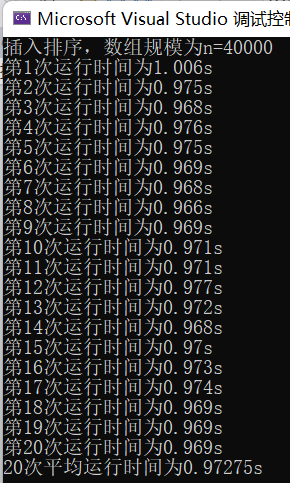
图表 9 n=40000不同排序平均时间
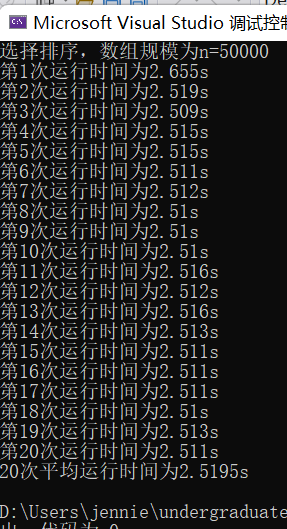
(5)输入规模n=50000不同排序平均时间(如图10)
选择排序t1 = 2.5195s
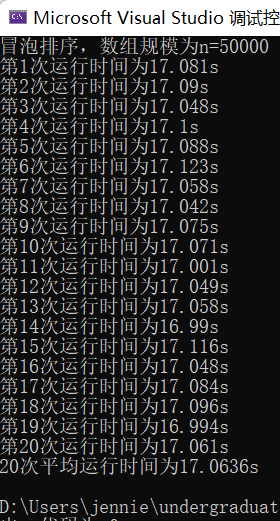
冒泡排序t2 = 17.0636s
合并排序t3 = 0.0069s
快速排序t4 = 0.0049s
插入排序t5 = 1.5176s


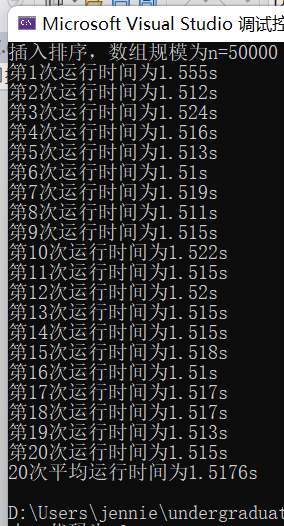
图表 10 n=50000不同排序平均时间
| 数据规模n | 10000 | 20000 | 30000 | 40000 | 50000 |
|---|---|---|---|---|---|
| 选择排序 | 0.1325 | 0.41825 | 0.92415 | 1.60885 | 2.5195 |
| 冒泡排序 | 0.6901 | 2.7229 | 6.136 | 10.9242 | 17.0636 |
| 合并排序 | 0.0012 | 0.0025 | 0.004 | 0.00545 | 0.0069 |
| 快速排序 | 0.00085 | 0.00175 | 0.00275 | 0.00385 | 0.0049 |
| 插入排序 | 0.0678 | 0.25925 | 0.55435 | 0.97275 | 1.5176 |
图表 11 5种算法平均用时统计(单位:秒)
2.不同排序算法在 20 个随机样本的平均运行时间与输入规模 n 的关系(如图12)
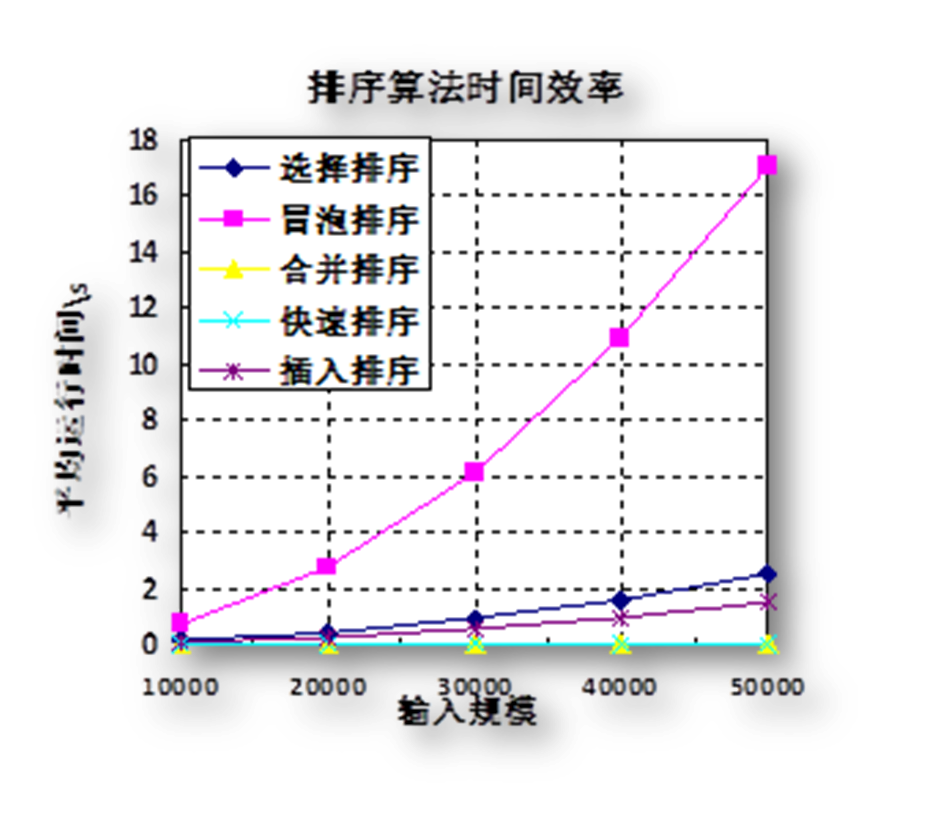
图表 12 时间效率与输入规模 n 的关系图
3.画出理论效率分析的曲线和实测的效率曲线,注意:由于实测效率是运行时间,而理论效率是基本操作的执行次数,两者需要进行对应关系调整。调整思路:以输入规模为10000 的数据运行时间为基准点,计算输入规模为其他值的理论运行时间,画出不同规模数据的理论运行时间曲线,并与实测的效率曲线进行比较。经验分析与理论分析是否一致?如果不一致,请解释存在的原因。
答: 选择排序、冒泡排序、插入排序的时间复杂度都是O(n2),那么n=10000,n=20000, n=30000, n=40000, n=50000的理论运行时间比应该是100002 : 200002 : 300002 : 400002 : 500002 , 即1 : 4 : 9 : 16 : 25;
则以输入规模为10000 的数据运行时间为基准点,即参照输入规模n=10000不同排序平均时间——选择排序t1 = 0.1325s,冒泡排序t2 = 0.6901s,插入排序t5 = 0.0678s,可得以下理论效率数据:(如图13-15)
| 数据规模 | 10000 | 20000 | 30000 | 40000 | 50000 |
|---|---|---|---|---|---|
| 实际 | 0.1325 | 0.41825 | 0.92415 | 1.60885 | 2.5195 |
| 理论 | 0.1325 | 0.53 | 1.1925 | 2.12 | 3.3125 |
图表 13 选择排序理论和实测用时(单位:秒)
| 冒泡排序 | 10000 | 20000 | 30000 | 40000 | 50000 |
|---|---|---|---|---|---|
| 实际 | 0.6901 | 2.7229 | 6.136 | 10.9242 | 17.0636 |
| 理论 | 0.6902 | 2.7604 | 6.2109 | 11.0416 | 17.2525 |

图表 14 冒泡排序理论和实测用时(单位:秒)
| 数据规模n | 10000 | 20000 | 30000 | 40000 | 50000 |
|---|---|---|---|---|---|
| 实际 | 0.0678 | 0.25925 | 0.55435 | 0.97275 | 1.5176 |
| 理论 | 0.0678 | 0.2712 | 0.6102 | 1.0848 | 1.695 |

图表 15 插入排序理论和实测用时(单位:秒)
同理合并排序、快速排序的时间复杂度都是O(nlog2n),那么n=10000,n=20000, n=30000, n=40000, n=50000的理论运行时间比应该是10000log210000 : 20000log220000 : 30000log230000 : 40000log240000 : 50000log250000 ,即1 : (0.5lg2+2) : (0.75lg3+3) : (2lg2+4) : (1.25lg5+5)。
则以输入规模为10000 的数据运行时间为基准点,即参照输入规模n=10000不同排序平均时间——合并排序t3 = 0.0012s,快速排序t4 = 0.00085s,可得以下理论效率数据(不完全以n=10000,做了部分优化):(如图16-17)
| 数据规模 | 10000 | 20000 | 30000 | 40000 | 50000 |
|---|---|---|---|---|---|
| 实际 | 1.2 | 2.5 | 4 | 5.45 | 6.9 |
| 理论 | 1.2 | 2.58 | 4.03 | 5.52 | 7.05 |

图表 16 合并排序理论和实测用时(单位:毫秒)
| 数据规模 | 10000 | 20000 | 30000 | 40000 | 50000 |
|---|---|---|---|---|---|
| 实际 | 0.83 | 1.75 | 2.75 | 3.85 | 4.9 |
| 理论 | 0.83 | 1.78 | 2.79 | 3.82 | 4.88 |
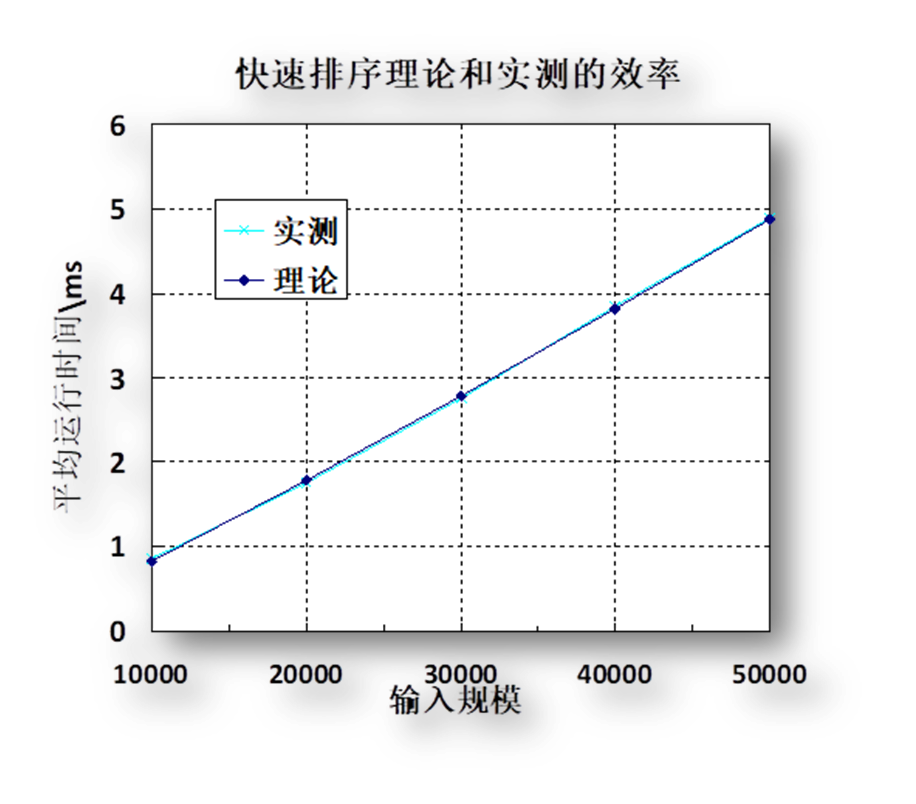
图表 17 快速排序理论和实测用时(单位:毫秒)
由图表基本可见,经验分析与理论分析基本一致。
结论
由上述实验过程可见,选择排序算法、冒泡排序算法和插入排序算法的时间复杂度为O(n2), 这意味着用该类算法,数据规模大到一定程度时,其运行时间将很大,时间的增长会随着数据成平方增长。 这对于大数据处理是比较不友好的。该类算法也是较为初期的排序算法,写法简单,逻辑易懂,但算力性价比不高,不适用于数据量较大时使用。
而合并排序算法和快速排序算法采用了采用分治法、递归的方法,将时间复杂度降为O(nlogn)。这在大数据排序的时候,就会比之前的算法有很大的优势。 比如在本次实验中将数据量提到5万的时候,该类算法运行时间仍在几毫秒左右,而上面的3种算法运行时间已经到达十几秒左右,效率相差已经到达万倍。该类算法的运行时间不会像上面的算法受数据增加的影响巨大,而是随着数据的增加,运行时间渐近线性的增加。但注意理论上快速排序的空间复杂度较高为O(n),且最坏情况时时间复杂度也达到了O(n2),运行时间结果变化较大,需要根据现实需求选择合适的算法。但现实中经过实际测试中它的效率很高,而一般空间是足够的,所以快速算法也较为常用。
所以综上,当面临巨大数据量的排序的时候,还是优先选择合并排序算法和快速排序算法。而选择排序算法、冒泡排序算法和插入排序算法不太适用于大数据排序。
现在有 1 亿的数据,请选择合适的排序算法与数据结构,在有限的时间内完成进行排序。
数据量较大,我选用了合并排序算法和快排(c++sort()函数),合并排序算法用时平均t1 = 18.6647s , 快排t2 = 39.8782s(如图18) 。从结果看出,合并算法的效率更高。

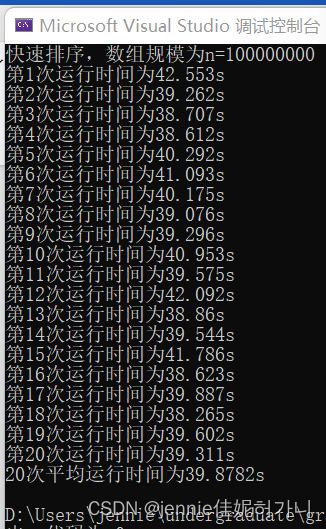
图表 18 1亿数据合并排序用时平均t1 = 18.6647s , 快排t2 = 39.8782



