卷积神经网络（CNN）详解_卷积神经网络详解

 

一、卷积神经网络的基本概念

       卷积神经网络与普通神经网络的区别在于，卷积神经网络包含了一个由卷积层和子采样层（池化层）构成的特征抽取器。在卷积神经网络的卷积层中，一个神经元只与部分邻层神经元连接。在CNN的一个卷积层中，通常包含若干个特征图(featureMap)，每个特征图由一些矩形排列的的神经元组成，同一特征图的神经元共享权值，这里共享的权值就是卷积核。卷积核一般以随机小数矩阵的形式初始化，在网络的训练过程中卷积核将学习得到合理的权值。共享权值（卷积核）带来的直接好处是减少网络各层之间的连接，同时又降低了过拟合的风险。子采样也叫做池化（pooling），通常有均值子采样（mean pooling）和最大值子采样（max pooling）两种形式。子采样可以看作一种特殊的卷积过程。卷积和子采样大大简化了模型复杂度，减少了模型的参数。

二、卷积神经网络的基本原理

2.1 神经网络

       首先介绍神经网络，神经网络的每个单元如下：

       其对应的公式如下：

       其中，该单元也可以被称作是Logistic回归模型。当将多个单元组合起来并具有分层结构时，就形成了神经网络模型。下图展示了一个具有一个隐含层的神经网络。

        其对应的公式如下：

       比较类似的，可以拓展到有2,3,4,5，…个隐含层。

       神经网络的训练方法也同Logistic类似，不过由于其多层性，还需要利用链式求导法则对隐含层的节点进行求导，即梯度下降+链式求导法则，专业名称为反向传播。关于训练算法的相关原理及操作过程，可参见之前写的关于BP算法https://blog.csdn.net/qq_42570457/article/details/81454008。

2.2 卷积神经网络

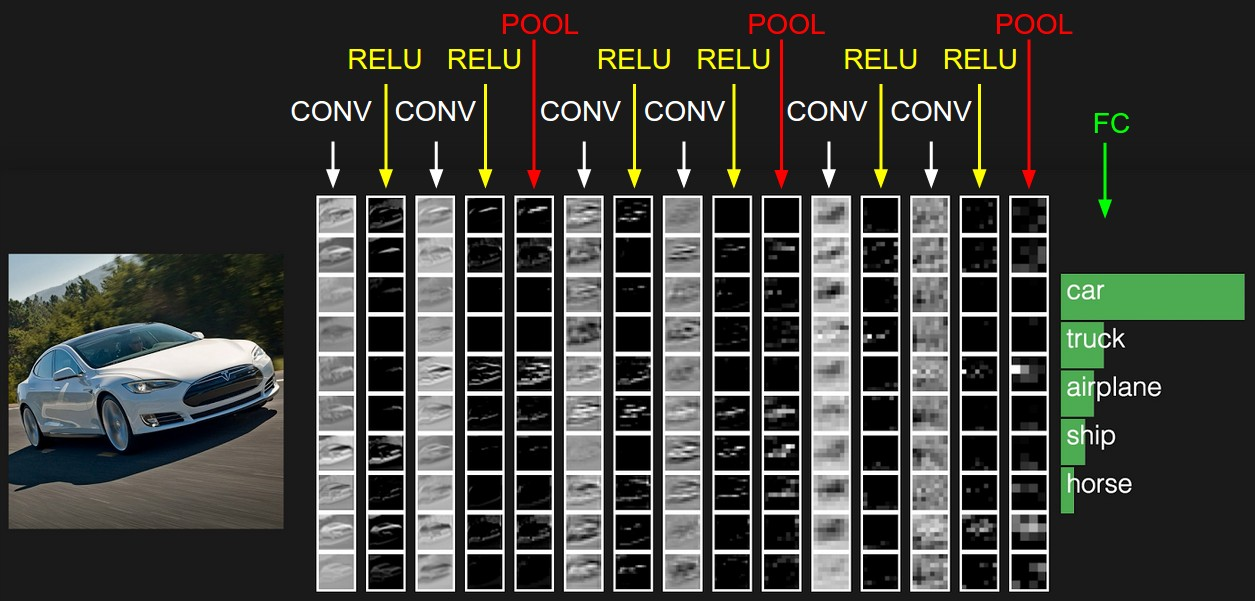
      首先，我们先获取一个感性认识，下图是一个卷积神经网络的实例：

卷积神经网络通常包含以下几种层：

• 卷积层（Convolutional layer），卷积神经网路中每层卷积层由若干卷积单元组成，每个卷积单元的参数都是通过反向传播算法优化得到的。卷积运算的目的是提取输入的不同特征，第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级，更多层的网络能从低级特征中迭代提取更复杂的特征。
• 线性整流层（Rectified Linear Units layer, ReLU layer），这一层神经的活性化函数（Activation function）使用线性整流（Rectified Linear Units, ReLU）f(x)=max(0,x)f(x)=max(0,x)。
• 池化层（Pooling layer），通常在卷积层之后会得到维度很大的特征，将特征切成几个区域，取其最大值或平均值，得到新的、维度较小的特征。
• 全连接层（ Fully-Connected layer）, 把所有局部特征结合变成全局特征，用来计算最后每一类的得分。

2.2.1 卷积层（Convolutional layer）

       卷积层是卷积神经网络的核心基石。在图像识别里我们提到的卷积是二维卷积，即离散二维滤波器（也称作卷积核）与二维图像做卷积操作，简单的讲是二维滤波器滑动到二维图像上所有位置，并在每个位置上与该像素点及其领域像素点做内积。卷积操作被广泛应用与图像处理领域，不同卷积核可以提取不同的特征，例如边沿、线性、角等特征。在深层卷积神经网络中，通过卷积操作可以提取出图像低级到复杂的特征。

       上图给出一个卷积计算过程的示例图，输入图像大小为H=5,W=5,D=3，即5×5大小的3通道（RGB，也称作深度）彩色图像。这个示例图中包含两（用K表示）组卷积核，即图中滤波器W0和W1。在卷积计算中，通常对不同的输入通道采用不同的卷积核，如图示例中每组卷积核包含（D=3）个3×3（用F×F表示）大小的卷积核。另外，这个示例中卷积核在图像的水平方向（W方向）和垂直方向（H方向）的滑动步长为2（用S表示）；对输入图像周围各填充1（用P表示）个0，即图中输入层原始数据为蓝色部分，灰色部分是进行了大小为1的扩展，用0来进行扩展。经过卷积操作得到输出为3×3×2（用Ho×Wo×K表示）大小的特征图，即3×3大小的2通道特征图，其中Ho计算公式为：Ho=(H−F+2×P)/S+1，Wo同理。 而输出特征图中的每个像素，是每组滤波器与输入图像每个特征图的内积再求和，再加上偏置bo，偏置通常对于每个输出特征图是共享的。输出特征图o[:,:,0]中的最后一个−2计算如上图右下角公式所示。

记住这几个符号：

• H：图片高度；
• W：图片宽度；
• D：原始图片通道数，也是卷积核个数；
• F：卷积核高宽大小；
• P：图像边扩充大小；
• S：滑动步长。
• K： 深度，输出单元的深度

       在卷积操作中卷积核是可学习的参数，经过上面示例介绍，每层卷积的参数大小为D×F×F×K。卷积层的参数较少，这也是由卷积层的主要特性即局部连接和共享权重所决定。

• 局部连接：每个神经元仅与输入神经元的一块区域连接，这块局部区域称作感受野（receptive field）。在图像卷积操作中，即神经元在空间维度（spatial dimension，即上图示例H和W所在的平面）是局部连接，但在深度上是全部连接。对于二维图像本身而言，也是局部像素关联较强。这种局部连接保证了学习后的过滤器能够对于局部的输入特征有最强的响应。局部连接的思想，也是受启发于生物学里面的视觉系统结构，视觉皮层的神经元就是局部接受信息的。
• 权重共享：计算同一个深度切片的神经元时采用的滤波器是共享的。例上图中计算o[:,:,0]的每个每个神经元的滤波器均相同，都为W0，这样可以很大程度上减少参数。共享权重在一定程度上讲是有意义的，例如图片的底层边缘特征与特征在图中的具体位置无关。但是在一些场景中是无意的，比如输入的图片是人脸，眼睛和头发位于不同的位置，希望在不同的位置学到不同的特征 。请注意权重只是对于同一深度切片的神经元是共享的，在卷积层，通常采用多组卷积核提取不同特征，即对应不同深度切片的特征，不同深度切片的神经元权重是不共享。另外，偏重对同一深度切片的所有神经元都是共享的。

通过介绍卷积计算过程及其特性，可以看出卷积是线性操作，并具有平移不变性（shift-invariant），平移不变性即在图像每个位置执行相同的操作。卷积层的局部连接和权重共享使得需要学习的参数大大减小，这样也有利于训练较大卷积神经网络。

整体计算过程如下（与上图中的数据不同，但是计算过程相同）：

 

2.2.2 线性整流层（Rectified Linear Units layer, ReLU layer）--激励层
       把卷积层输出结果做非线性映射。

       CNN采用的激励函数一般为ReLU(The Rectified Linear Unit/修正线性单元)，它的特点是收敛快，求梯度简单，但较脆弱，图像如下。

 

激励层的实践经验：
　　①不要用sigmoid！不要用sigmoid！不要用sigmoid！
　　② 首先试RELU，因为快，但要小心点
　　③ 如果2失效，请用Leaky ReLU或者Maxout
　　④ 某些情况下tanh倒是有不错的结果，但是很少

2.2.3 池化层（Pooling layer）

       池化（pool）即下采样（downsamples），目的是为了减少特征图，主要作用是通过减少网络的参数来减小计算量，并且能够在一定程度上控制过拟合。通常在卷积层的后面会加上一个池化层。池化操作对每个深度切片独立，规模一般为 2＊2，相对于卷积层进行卷积运算，池化层进行的运算一般有以下几种： 
      * 最大池化（Max Pooling）。取4个点的最大值。这是最常用的池化方法。 
     * 均值池化（Mean Pooling）。取4个点的均值。 
     * 高斯池化。借鉴高斯模糊的方法。不常用。 
     * 可训练池化。训练函数 ff ，接受4个点为输入，出入1个点。不常用。

最常见的池化层是规模为2*2， 步幅为2，对输入的每个深度切片进行下采样。每个MAX操作对四个数进行，如下图所示： 

       

      池化操作将保存深度大小不变。如果池化层的输入单元大小不是二的整数倍，一般采取边缘补零（zero-padding）的方式补成2的倍数，然后再池化。

2.2.4 全连接层（ Fully-Connected layer）

全连接层和卷积层可以相互转换： 
       * 对于任意一个卷积层，要把它变成全连接层只需要把权重变成一个巨大的矩阵，其中大部分都是0 除了一些特定区块（因为局部感知），而且好多区块的权值还相同（由于权重共享）。 
    * 相反地，对于任何一个全连接层也可以变为卷积层。

2.2.5 反向传播

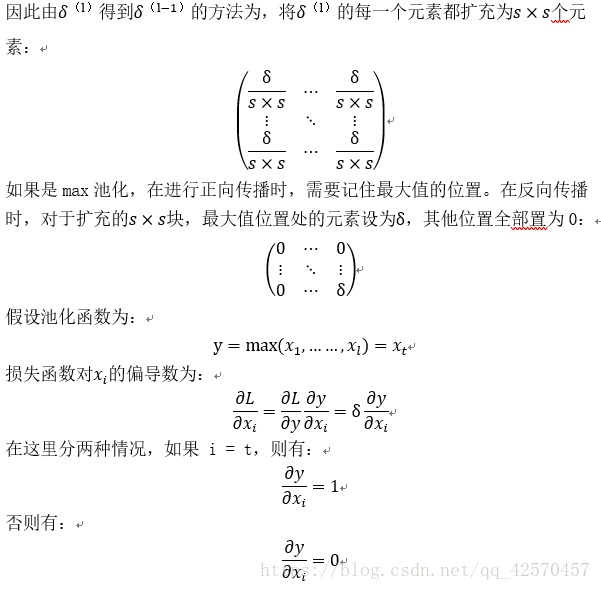
下面讲解卷积层的反向传播过程：

（由于公式格式不太好整理，所以用截图代替）

其他关于反向传播的介绍：

https://mp.weixin.qq.com/s?__biz=MzU4MjQ3MDkwNA==&mid=2247485971&idx=1&sn=632e3c135ead5f0ac730eee5b6a05647&chksm=fdb69784cac11e9258f67312fa2798e9c8210b8f77741a3d7bab4c1ccfa1c1f66632183f4f26&scene=0#rd

http://www.cnblogs.com/pinard/p/6494810.html

三、其他

一般CNN结构依次为
　　1. INPUT
　　2. [[CONV -> RELU]*N -> POOLING]*M 
　　3. [FC -> RELU]*K
　　4. FC

卷积神经网络之训练算法
　　1. 同一般机器学习算法，先定义Loss function，衡量和实际结果之间差距。
　　2. 找到最小化损失函数的W和b， CNN中用的算法是SGD（随机梯度下降）。

卷积神经网络之优缺点
优点
　　• 共享卷积核，对高维数据处理无压力
　　• 无需手动选取特征，训练好权重，即得特征分类效果好
缺点
　　• 需要调参，需要大样本量，训练最好要GPU
　　• 物理含义不明确（也就说，我们并不知道没个卷积层到底提取到的是什么特征，而且神经网络本身就是一种难以解释的“黑箱模型”）

卷积神经网络之典型CNN
　　• LeNet，这是最早用于数字识别的CNN
　　• AlexNet， 2012 ILSVRC比赛远超第2名的CNN，比
　　• LeNet更深，用多层小卷积层叠加替换单大卷积层。
　　• ZF Net， 2013 ILSVRC比赛冠军
　　• GoogLeNet， 2014 ILSVRC比赛冠军
　　• VGGNet， 2014 ILSVRC比赛中的模型，图像识别略差于GoogLeNet，但是在很多图像转化学习问题(比如object detection)上效果奇好