到底什么是机器学习模型？这篇文章终于讲明白了

机器学习 (Machine Learning) 是对研究问题进行模型假设，利用计算机从训练数据中学习得到模型参数，并最终对数据进行预测和分析的一门学科。

**模型是机器学习的核心组成要素。**本文从模型的广义概念出发，引申出机器学习模型的基本定义，并就机器学习中容易混淆的概念——模型和算法，进行了详细对比和关系解读，最后列出了常见的模型评估指标与方法，供大家在学习机器学习的过程中起到一点参考作用。

1.模型的基本定义

先来看看百度百科对于模型的定义：从广义上讲：如果一件事物能随着另一件事物的改变而改变，那么此事物就是另一件事物的模型。模型的作用就是表达不同概念的性质，一个概念可以使很多模型发生不同程度的改变，但只要很少模型就能表达出一个概念的性质，所以一个概念可以通过参考不同的模型从而改变性质的表达形式。

当模型与事物发生联系时会产生一个具有性质的框架，此性质决定模型怎样随事物变化。

模型由三个部分组成的，即目标、变量和关系。

数学模型：用数学语言描述的一类模型。数学模型可以是一个或一组代数方程、微分方程、差分方程、积分方程或统计学方程，也可以是它们的某种适当的组合，通过这些方程定量地或定性地描述系统各变量之间的相互关系或因果关系。除了用方程描述的数学模型外，还有用其他数学工具，如代数、几何、拓扑、数理逻辑等描述的模型。需要指出的是，数学模型描述的是系统的行为和特征而不是系统的实际结构。

那么什么是机器学习模型？

机器学习模型其实是一种映射，可以将其看作是在给定输入情况（x）下、输出一定结果的函数f(x),如下图所示：

**机器学习模型本质上是一种接受数据作为输入并生成输出的函数，**在利用已知数据去预测未知数据的过程中，模型不仅要在已知样本上表现优秀，更要在未知样本上具有相近的表现。

由此，我们可以引申出机器学习的定义：机器学习的概念就是通过输入海量训练数据对模型进行训练，使模型掌握数据所蕴含的潜在规律，进而对新输入的数据进行准确的分类或预测。

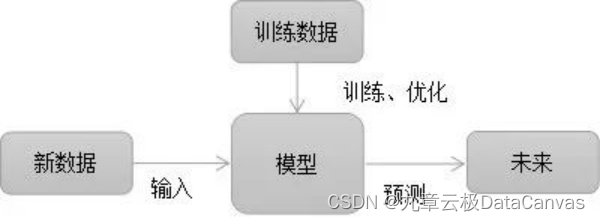
机器学习的核心是“使用算法解析数据，从中学习，然后对新数据做出决定或预测”。也就是说计算机利用已获取的数据得出某一模型，然后利用此模型进行预测的一种方法，这个过程跟人的学习过程有些类似，比如人获取一定的经验，可以对新问题进行预测。

2.机器学习中算法与模型的区别：

**算法：**算法是指完成一个任务所需要的具体步骤和方法。也就是说给定初始状态或输入数据，经过计算机程序的有限次运算，能够得出所要求或期望的终止状态或输出数据。

机器学习中的“算法”是在数据上运行以创建机器学习“模型”的过程。

机器学习算法有很多，例如线性回归、逻辑回归、决策树、人工神经网络、K- 最近邻、K- 均值等等。你可以把机器学习算法想象成计算机科学中的任何其他算法。

**模型：**机器学习中的“模型”是运行在数据上的机器学习算法的输出。
模型表示机器学习算法所学到的内容。

模型是在训练数据上运行机器学习算法后保存的“东西”，它表示用于进行预测所需的规则、数字和任何其他特定于算法的数据结构。

举一些例子，可能会让人更清楚地明白这一点：

线性回归算法的结果是一个由具有特定值的稀疏向量组成的模型。
决策树算法的结果是一个由具有特定值的 if-then 语句树组成的模型。
神经网络 / 反向传播 / 梯度下降算法一起产生一个由具有特定值的向量或权重矩阵和特定值的图结构组成的模型。

算法和模型的关系

现在我们已经熟悉了机器学习的“算法”和机器学习的“模型”。
具体来说，就是对数据运行算法来创建模型。
下图这个公式可以更好地帮助我们理解算法和模型的关系。

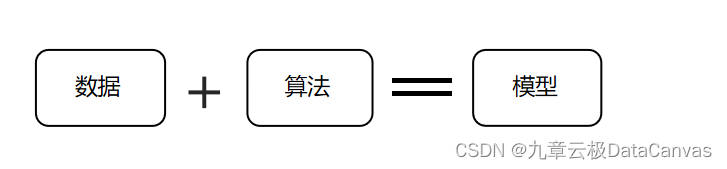
我们了解到，模型由数据和如何使用数据对新数据进行预测的过程组成。

如果将机器学习模型想象成一个“程序”，那么机器学习模型“程序”由数据和利用数据进行预测的过程组成。

通常情况下，算法是某种优化程序，即在训练数据集上使模型（数据 + 预测算法）的误差最小化。线性回归算法就是一个很好的例子。它执行一个优化过程（或用线性代数进行分析求解），找到一组权重，使训练数据集上的误差之和平方最小化。

例如，考虑线性回归算法和由此产生的模型。该模型由系数（数据）向量组成，这些系数（数据）与作为输入的一行新数据相乘并求和，以便进行预测（预测过程）。

我们将数据保存为机器学习模型，以备后用。

机器学习是自动编程

我们真的只是想要一个机器学习的“模型”，而“算法”就是我们获得模型的路径。

机器学习技术用于解决其他方法无法有效或高效解决的问题。

例如，如果我们需要将电子邮件分类为垃圾邮件或非垃圾邮件，我们需要一个软件程序来完成此任务。

我们可以坐下来，手动查看大量的电子邮件，然后写 if 语句来完成合格任务。人们已经试过这个方法。事实证明，这种方法是缓慢的、脆弱的，而且效果也不是很好。

相反，我们可以使用机器学习技术来解决这个问题。具体来说，像 朴素贝叶斯（Naive Bayes）这样的算法就可以从大量的历史邮件样本数据集中学习如何将邮件分类为垃圾邮件和非垃圾邮件。

我们不想要“朴素的贝叶斯”，我们想要朴素贝叶斯给出的模型，就是我们可以用来对邮件进行分类的模型（概率向量和使用概率概率的预测算法）。我们想要的是模型，而不是用来创建模型的算法。

从这个意义上来说，机器学习模型是一个由机器学习算法自动编写、或创建、或学习的程序，用来解决我们的问题。

机器学习算法执行自动编程，而机器学习模型是为我们创建的程序。

3.衡量模型性能的指标

什么是模型评估

模型评估是对训练好的模型性能进行评估, 模型评估是模型开发过程不可或缺的一部分。它有助于发现表达数据的最佳模型和所选模型将来工作的性能如何。

模型评估的类型

机器学习的任务有回归,分类和聚类，针对不同的任务有不同的评价指标。按照数据集的目标值不同，可以把模型评估分为分类模型评估和回归模型评估。

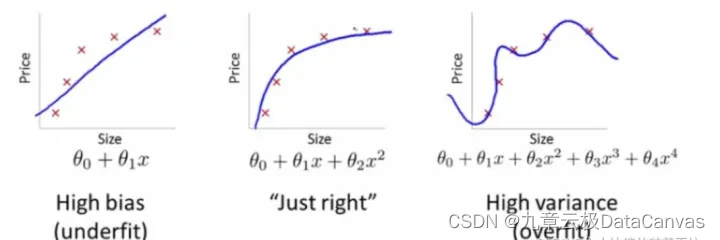
过拟合、欠拟合

1）欠拟合

欠拟合（或称：拟合不足、欠配，英文：underfitting）是指模型在训练数据上没有获得充分小的误差．造成欠拟合的原因通常是模型学习能力过低，具体地说，就是模型参数过少或者结构过于简单，以至于无法学习到数据的内在结构和特征．例如，当用一个线性模型去拟合非线性数据时，会发生欠拟合．由此，可以通过增加模型参数和复杂度，提高学习能力，从而解决欠拟合问题．与欠拟合相对应的，是过度拟合．

2）过拟合

是指为了得到一致假设而使假设变得过度严格。
避免过拟合是分类器设计中的一个核心任务。
通常采用增大数据量和测试样本集的方法对分类器性能进行评价。
无论是欠拟合还是过拟合，都是模型泛化能力差的表现。

模型泛化能力
泛化能力（generalization ability）是指机器学习算法对新鲜样本的适应能力。

机器学习的目的是学到隐含在数据背后的规律，对具有同一规律的学习集以外的数据，经过训练的网络也能给出合适的输出，该能力称为泛化能力。

规律适用于现有数据，同样也适用于新鲜数据。

常见的分类模型评估指标有：

1）混淆矩阵：混淆矩阵是监督学习中的一种可视化工具，主要用于模型的分类结果和实例的真实信息的比较 。

矩阵中的每一行代表实例的预测类别，每一列代表实例的真实类别。
2）准确率Accuracy：准确率是最常用的分类性能指标。
Accuracy = (TP+TN)/(TP+FN+FP+TN)
预测正确的数占样本总数的比例，即正确预测的正反例数 /总数。

3）精确率（Precision）：精确率只是针对预测正确的正样本而不是所有预测正确的样本。

表现为预测出是正的里面有多少真正是正的。可理解为查准率。
Precision = TP/(TP+FP)
即正确预测的正例数 /预测正例总数

4）召回率recall：率表现出在实际正样本中，分类器能预测出多少。
与真正率相等，可理解为查全率。正确预测为正占全部正校本的比例
Recall = TP/(TP+FN)，即正确预测的正例数 /实际正例总数

5）F1-score：主要用于评估模型的稳健性

6）AUC指标：主要用于评估样本不均衡的情况

7）AUC：随机挑选一个正样本以及一个负样本，分类器判定正样本的值高于负样本的概率就是 AUC 值。

8）PR曲线：PR曲线的横坐标是精确率P，纵坐标是召回率R。

常见的回归模型评估指标有：

1）向量的距离

·欧式距离/几何距离

·曼哈顿距离

·马氏距离

·余弦距离

2）平均绝对误差（MAE）
平均绝对误差MAE（Mean Absolute Error）又被称为l1范数损失（l1-norm loss）

3）平均平方误差（MSE）
平均平方误差MSE（Mean Squared Error）又被称为l2范数损失（l2-norm loss）

4）均方根误差（RMSE）
RMSE虽然广为使用，但是其存在一些缺点，因为它是使用平均误差，而平均值对异常点（outliers）较敏感，如果回归器对某个点的回归值很不理性，那么它的误差则较大，从而会对RMSE的值有较大影响，即平均值是非鲁棒的。

5）解释变异
解释变异（ Explained variance）是根据误差的方差计算得到的。

6）决定系数
决定系数（Coefficient of determination）又被称为R2。

常见的聚类模型评估指标：

1）兰德指数：兰德指数（Rand index）需要给定实际类别信息C，假设K是聚类结果，a表示在C与K中都是同类别的元素对数，b表示在C与K中都是不同类别的元素对数，则兰德指数为：

2）互信息

互信息（Mutual Information）也是用来衡量两个数据分布的吻合程度。

3）轮廓系数
轮廓系数（Silhouette coefficient）适用于实际类别信息未知的情况。