数模线性规划问题基本原理及Python编程实现_python线性规划模型求解代码

转来转去又转到了Python（可能我与Python有缘）

一： python求解线线性规划问题

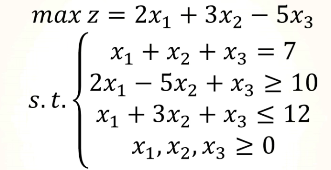
使用scipy这个包求解线性规划问题

from scipy import optimize
import numpy as np

# 确定c A B Aeq Beq
c = np.array([2, 3, -5])
A = np.array([[-2, 5, -1], [1, 3, 1]])
B = np.array([-10, 12])
Aeq = np.array([[1, 1, 1]])
Beq = np.array([7])

# 求解
res = optimize.linprog(-c, A, B, Aeq, Beq)
print(res)
1
2
3
4
5
6
7
8
9
10
11
12
13

运行结果：

con: array([1.80714554e-09])
     fun: -14.571428565645032
 message: 'Optimization terminated successfully.'
     nit: 5
   slack: array([-2.24602559e-10,  3.85714286e+00])
  status: 0
 success: True
       x: array([6.42857143e+00, 5.71428571e-01, 2.35900788e-10])
1
2
3
4
5
6
7
8

使用pulp这个包来求解线性规划问题

首先，需要了解下pulp中的一些函数

1. LpProblem类
LpProblem(name='NoName', sense=LpMinimize)
构造函数，用来构造一个LP问题实例，其中name指定问题名（输出信息用)，
sense值是LpMinimize或LpMaximize中的一个，用来指定目标函数是求极大值还是极小值。
2.solve(solver=None, **kwargs)
在对LpProblem添加完约束条件后，调用该函数进行求解，如果不是求解特定的整数规划问题，solver一般使用默认即可。
3. LpVariable类
LpVariable(name, lowBound=None, upBound=None, cat='Continuous', e=None)
构造函数，用来构造LP问题中的变量，name指定变量名，lowBound和upBound是下界和上界，
默认分别是负无穷到正无穷,cat用来指定变量是离散(Integer,Binary)还是连续(Continuous)。
4.lpDot
可以将两个列表的对应位相乘再相加
比如
pulp.lpDot(z,x)
# z[0]*x[0]+z[1]*x[1]+z[2]*x[2]...
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

import pulp
# 目标函数的系数
z = [2, 3, 1]
# 约束
a = [[1, 4, 2], [3, 2, 0]]
b = [8, 6]
# 确定最大化最下化问题，最大化只要把Min改成Max即可
m = pulp.LpProblem(sense=pulp.LpMinimize)
# 定义三个变量放到列表中
x = [pulp.LpVariable(f'x{i}', lowBound=0) for i in [1, 2, 3]]
# 定义目标函数
m += pulp.lpDot(z, x)
# 设置约束条件
for i in range(len(a)):
    m += (pulp.lpDot(a[i], x) >= b[i])
# 求解
m.solve()
# 输出结果
print(f'优化结果:{pulp.value(m.objective)}')
print(f'参数取值:{[pulp.value(var) for var in x]}')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

运行结果

优化结果:7.0
参数取值:[2.0, 0.0, 3.0]
1
2
'
运行
运行

二：示例

运输问题：1.

（其实想一想这模型挺巧的，可能我是小白的原因…）

运输问题：2.

import pulp
import numpy as np
from pprint import pprint


def transportation_problem(costs, x_max, y_max):
    row = len(costs)
    col = len(costs[0])
    prob = pulp.LpProblem('Transportation Problem', sense=pulp.LpMaximize)
    var = [[pulp.LpVariable(f'x{i}{j}', lowBound=0, cat=pulp.LpInteger) for j in range(col)] for i in range(row)]
    flatten = lambda x: [y for l in x for y in flatten(l)] if type(x) is list else [x]
    prob += pulp.lpDot(flatten(var), costs.flatten())
    for i in range(row):
        prob += (pulp.lpSum(var[i]) <= x_max[i])
    for j in range(col):
        prob += (pulp.lpSum([var[i][j] for i in range(row)]) <= y_max[j])
    prob.solve()
    return {'objective': pulp.value(prob.objective),
            'var': [[pulp.value(var[i][j]) for j in range(col)] for i in range(row)]}


if __name__ == "__main__":
    costs = np.array([[500, 550, 630, 1000, 800, 700],
                      [800, 700, 600, 950, 900, 930],
                      [1000, 960, 840, 650, 600, 700],
                      [1200, 1040, 980, 860, 880, 780]])
    max_plant = [76, 88, 96, 40]
    max_cultivation = [42, 56, 44, 39, 60, 59]
    res = transportation_problem(costs, max_plant, max_cultivation)
    print(f'最大值为{res["objective"]}')
    print('各变量的取值为:')
    pprint(res['var'])

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

运行结果：

最大值为284230.0
各变量的取值为:
[[0.0, 0.0, 6.0, 39.0, 31.0, 0.0],
 [0.0, 0.0, 0.0, 0.0, 29.0, 59.0],
 [2.0, 56.0, 38.0, 0.0, 0.0, 0.0],
 [40.0, 0.0, 0.0, 0.0, 0.0, 0.0]]
1
2
3
4
5
6